基于阻尼功率调整的虚拟同步机有功功率控制方法

刘秦娥，任东风，康逸群，张鹏超，翟羽翔，贾凯阳，郭磊磊

（1.国网湖北襄阳供电公司，湖北襄阳 441000；2.国网湖北电力科学研究院，湖北武汉 430015；3.郑州轻工业大学电气信息工程学院，河南郑州 450002）

0 引言

为了实现“碳达峰、碳中和”的目标，近年来，光伏、风电等新能源发电装备大规模接入电网[1]。由于新能源存在的随机性、波动性、间歇性等问题，大规模新能源接入电网后对电网的稳定运行产生了较大影响[2]。为了实现新能源的灵活调度，增强新能源对大电网的支撑能力和适应能力，新能源电站往往需要配备一定容量的储能装置[3]。

虚拟同步机控制技术可以使储能逆变器模拟同步发电机的惯量和阻尼，显著增强其对电网的支撑能力[4-6]。近年来，各类储能逆变器虚拟同步机控制技术得到广泛关注和研究。然而，虽然引入阻尼系数可以抑制虚拟同步机有功功率参考值突变时的功率震荡和超调，但也会增大电网频率出现偏差时的有功功率稳态偏差[7]。针对该问题，近年来，国内外诸多学者开展了改进方案研究。主要改进方案包括设计惯量和阻尼系数自适应调整方法[8-10]和设计暂态阻尼方法[11-17]。文献[8-10]研究了基于虚拟同步机运行状态自适应调整虚拟惯量和阻尼的方法。虽然这类方法有助于减小有功功率震荡、超调和偏差，但仍无法完全解决两者之间的矛盾问题。文献[11-17]探讨了基于暂态阻尼的虚拟同步机有功功率控制方法，通过在有功功率控制环路中增加前馈、反馈等环节，使系统在暂态时阻尼较大，而在稳态时阻尼为零，既可以实现有功功率动态震荡和超调的抑制，又可以实现稳态有功功率偏差的消除。其中，文献[11]研究了一种基于有功功率暂态前馈补偿和暂态反馈补偿的虚拟同步机有功功率控制方法，并通过仿真和实验研究证明了所提方法的有效性。然而，文中所提方法需要使用微分运算，易放大噪声的影响，降低系统稳定性。文献[12]提出了一种基于一阶微分补偿环节和一阶惯性环节的虚拟同步机有功功率控制方法。虽然该方法也可以实现有功功率震荡、超调的抑制，并消除稳态有功功率偏差，但系统参数设计方法较复杂。文献[13]设计了一种具有暂态阻尼特性的虚拟同步机有功功率控制方法。该方法在虚拟同步机的阻尼回路中引入一个高通滤波器，使虚拟同步机的阻尼仅在动态过程中起作用，而在稳态时阻尼自动减小为零，很好地解决了有功功率动态震荡与稳态偏差之间的矛盾。然而，该方法同样需要使用微分运算，易放大系统高频噪声的影响。为了避免使用微分运算，文献[14-15]研究了基于带通滤波器的虚拟同步机暂态阻尼设计方法。然而，这种方法导致系统的阶次由2 提升为4，系统参数设计过程非常复杂。文献[16]研究了一种基于有功功率微分前馈补偿的储能型虚拟同步机有功功率控制方法。然而，该方法同样需要进行微分运算。文献[17]引入了分数阶微分算法，设计了一种基于有功功率分数阶微分校正的储能型虚拟同步机有功功率控制方法。虽然该方法可以解决有功功率动态震荡与稳态偏差之间的矛盾，但分数阶微分算法的实现较困难。

为了解决常规虚拟同步机存在的有功功率动态震荡、超调和稳态误差之间的矛盾，并不使用微分运算，简化算法的实现过程，本文提出了一种基于阻尼功率比例积分调整的虚拟同步机有功功率控制方法。Matlab/Simulink 对比仿真结果验证了所提方法的有效性。

1 常规虚拟同步机控制策略及其问题分析

1.1 常规虚拟同步机控制策略

图1 给出了本文所研究的虚拟同步机主电路拓扑及其控制策略的控制框图。其中ω0为电网电压的额定角频率，ω为虚拟同步机输出的角频率，kω为等效下垂系数，Pref为给定的参考有功功率，Pe为虚拟同步机输出的有功功率，PD为阻尼功率，满足PD=Dω0（ω-ω0），D为阻尼系数，J为虚拟惯量，q1为估计的电网电压相位，ea，eb，ec为三相电网电压，ia，ib，ic为三相电网电流，ua，ub，uc为三相采样电压，Zg为电网线路阻抗，L为滤波电感，C为滤波电容，E为虚拟同步机输出电压幅值，Qref为无功指令值，Qe为输出无功功率；Δω1为角频率变化量；ΔP1为第一功率偏差，ΔP1=kω（ω0-ω）；ΔP2为第二功率偏差，ΔP2=Pref+ΔP1-Pe，s为拉普拉斯算子。其控制策略主要包括有功功率控制、无功功率控制和电压电流双闭环控制等。本文重点分析常规虚拟同步机有功功率控制策略所存在的主要问题，并研究一种改进的控制策略。

图1 虚拟同步机主电路拓扑及其控制策略的控制框图Fig.1 Control block diagram of main circuit topology and control strategy for virtual synchronous generator

虚拟同步机控制技术可以使储能逆变器模拟同步发电机的惯量和虚拟，以增强储能逆变器的电网支撑能力。根据这一特性，虚拟同步机常规有功功率控制策略满足[18-22]：

式中：Pm为虚拟同步机输出的机械功率；t为时间。

1.2 常规控制策略问题分析

根据虚拟同步机控制原理和潮流计算原理，可得虚拟同步机输出的有功功率Pe计算方法为[23-28]：

式中：Eg为电网电压幅值；Xg为电网线路阻抗；δ为功角，即虚拟同步机输出角度与电网角度之差；ωg为电网角频率。

由式（1）和式（2）可得虚拟同步机输出有功功率的控制框图如图2 所示。图2 中，K=EgE/Xg。

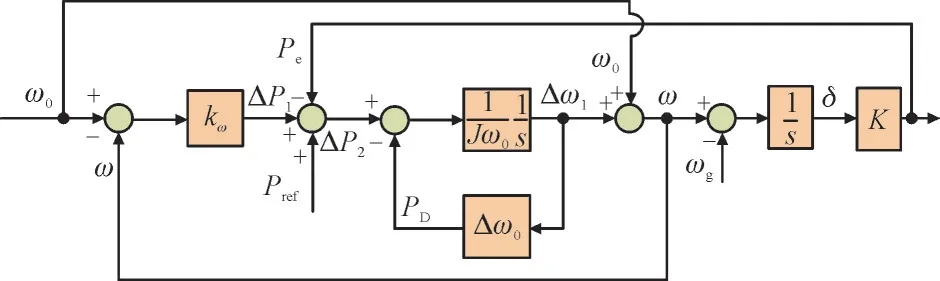
图2 虚拟同步机有功功率控制框图Fig.2 Control block diagram for active power of virtual synchronous generator

由图2 可以推导出常规虚拟同步机有功功率闭环控制传递函数G1满足：

式中：ΔPe为VSG 输出有功功率的变化量；ΔPref为VSG 有功指令值的变化量。

为了分析D对虚拟同步机常规有功功率控制动态特性的影响，本文借助Matlab 分析软件，利用step 函数分析不同D下的有功功率控制单位阶跃响应。这里取K=154 000（无量纲），J=0.5 kg/m2，kω=3 000 rad/W，ω0=314 rad/s。图3 给出了D由0 增大到20 时有功功率Pe随时间t的阶跃响应曲线，Δωg在0 时刻由0 突增为1 rad/s 时的有功功率Pe的变化曲线，其中标幺化的基值为10 kW。

图3 D变化时有功功率阶跃响应曲线Fig.3 Step response curves for active power when D changes

由图3 可见，当D为0 时，由于系统处于欠阻尼状态，有功功率出现了较大的震荡和超调。然而，随着D逐渐增大，系统逐渐由欠阻尼状态过度到过阻尼状态，有功功率震荡和超调得到明显抑制。由此可见，在虚拟同步机中引入虚拟阻尼控制，有助于实现有功功率震荡和超调的抑制。

由图2 还可得到频率偏差与有功功率偏差之间的传递函数G2，满足：

式中：Δωg为电网频率偏差，满足Δωg=ω0-ωg。

为了分析不同D下电网频率变化时虚拟同步机常规有功功率控制的动态特性，这里同样借助Matlab 分析软件，利用step 函数分析不同D下传递函数G2对应的有功功率单位阶跃响应。K，J，kω和ω0的取值与图3 相同。图4 给出了D由0 增大到20时有功功率Pe的阶跃响应曲线。

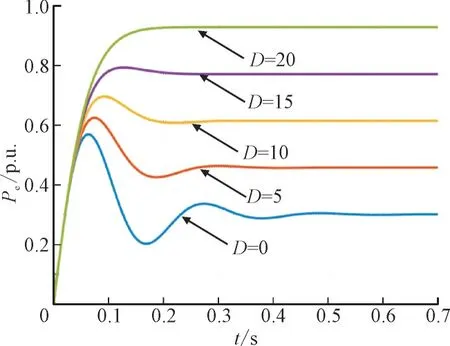
图4 频率变化、不同D值时有功功率阶跃响应曲线Fig.4 Step response curves for active power when frequency changes with different values of D

由图4 可见，当D为0 时，频率变化时有功功率存在明显的震荡。当D增大时，有功功率震荡得到显著抑制。然而，随着D的增加，有功功率出现了明显的稳态偏差。其原因分析结果如下：

首先，由式（4）可知，当电网频率出现偏差时，有功功率在稳态时也将出现偏差，且有功功率稳态偏差ΔPe满足：

式中：Dω0Δωg为由阻尼系数带来的功率偏差；kωΔωg为有功调频需要的功率偏差。

由式（5）可见，当D为0 时，有功功率稳态偏差ΔPe为kωΔωg，因此其单位阶跃响应结果（即Δωg=1）为ΔPe=3 000 W，与图4 中D=0 的曲线一致。当D增大时，由式（5）可见，ΔPe相应也会增大，这也与图4 分析结果一致。

由对图3、图4、式（5）的分析可知，随着D的增大，有功功率震荡和超调可以得到抑制，但由图4和式（5）可知有功功率偏差将显著增大。为此，有必要研究改进的虚拟同步机有功功率控制策略，以同时实现有功功率震荡和超调抑制，并消除有功功率稳态偏差。

2 改进的虚拟同步机控制策略

2.1 改进的控制策略

由图2 可知，在虚拟同步机运行到稳态时，在积分器的作用下将有ω=ωg。此时可得：

由式（5）和式（6）可得：

由式（6）和（7）可见，虚拟同步机在电网频率出现偏差时存在有功功率稳态偏差的本质原因在于阻尼功率PD会随D的增大而增大。因此，为了消除有功功率稳态偏差，在稳态时应该使阻尼功率PD为零。

为此，本文提出了一种基于阻尼功率比例积分调整的虚拟同步机改进型有功功率控制策略。所提方法的控制框图如图5 所示，kP和kI分别为本文引入的比例积分控制器的比例系数和积分系数，Δω2为补偿的角频率变化量。

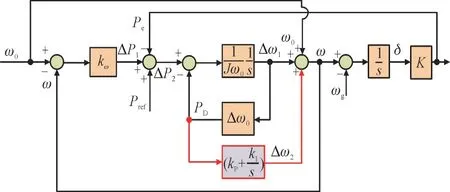
图5 所提虚拟同步机有功功率控制方法Fig.5 The proposed active power control method for virtual synchronous generator

2.2 改进控制策略分析

由图5 可以得到改进的虚拟同步机有功功率闭环控制传递函数G3满足：

式中：m1和m2为系数，m1=Dω0+kω+Dω0kPkω，m2=Dω0kIkω+K+Dω0kPK。

由式（8）可见，当kP=kI=0 时，G3和G1相同。此时，改进的虚拟同步机有功功率策略与常规方法相同。而当kP和kI不为0 时，则可以利用kP和kI改善有功功率的动态性能，并消除稳态有功功率偏差。为了分析kP，kI和D对虚拟同步机有功功率控制动态特性的影响，借助Matlab 分析软件，利用step 函数分析不同kP，kI和D下的有功功率控制单位阶跃响应。分析时，取K=154 000（无量纲），J=0.5 kg/m2，kω=3 000 rad/W，ω0=314 rad/s。分析结果如图6 所示。

图6 不同参数取值时有功功率阶跃响应曲线Fig.6 Step response curves for active power with different parameters

图6（a）给出了D=15，kP=0.001，kI由0 按步长0.005 增大到0.02 时的有功功率控制单位阶跃响应曲线。图6（b）给出了D=15，kI=0.02，kP由0 按步长0.000 3 增大到0.001 时的有功功率控制单位阶跃响应曲线。图6（c）给出了kP=0.001，kI=0.02，D由0按步长5 增大到15 时的有功功率控制单位阶跃响应曲线。图6（d）给出了kP=0.001，kI=0.02，D=15和kP=kI=0，D=15 时的有功功率控制单位阶跃响应曲线。

由图6（a）可见，当仅增大积分系数kI时，有功功率的超调略有增大。由图6（b）可见，当仅增大比例系数kP时，有功功率的震荡和超调得到显著减小，动态响应加快。由图6（c）可见，当仅增大阻尼系数D时，有功功率的震荡和超调也显著减小。

综合图6（a）—（c）的分析，取kP=0.001，kI=0.02，D=15 时可得本文所提方法的有功功率单位阶跃响应如图6（d）所示。与常规方法相比（kP=0，kI=0，D=15），所提方法通过合理选择比例积分系数和阻尼系数，可以显著提高有功功率的动态响应性能，验证了本文所提方法的有效性。

由图5 还可得到频率偏差与有功功率偏差之间的传递函数G4，满足：

为了与式（4）和图4 所示常规方法进行对比，借助Matlab 分析软件，利用step 函数分析不同D下传递函数G4对应的有功功率控制单位阶跃响应。K，J，kω和ω0的取值与图4 一致。不同的是，改进方法增加了kP和kI2 个参数。根据图6 分析结果，取kP=0.001，kI=0.02。图7 给出了D由0 增大到20 时有功功率Pe的阶跃响应曲线。

图7 频率变化、不同D值时本文所提改进方法有功功率阶跃响应曲线Fig.7 Step response curves for active power when frequency changes with different values of D by the proposed method

由图7 可见，无论D取多大，有功功率在稳态时均为3 kW，始终满足ΔPe=kωΔωg，与图4 中D=0 的结果一致。可见，本文所提方法可以消除增大D带来的有功功率稳态偏差问题。与此同时，由图7 可见，随着D的增大，在频率突变时有功功率的震荡和超调也随之减小。由此可见，本文所提方法通过引入比例积分控制器对阻尼功率进行调整，可以很好地解决有功功率动态震荡和稳态静差之间的矛盾，实现更精确的有功功率控制。

由式（9）可知，当电网频率出现偏差时，有功功率偏差ΔPe满足：

对比式（5）和式（10）可见，本文所提方法通过引入比例积分控制器对PD进行调整，使稳态时PD减小为0，既保证了可以使用不为0 的D来减小动态时有功功率的震荡和超调，同时可以保证稳态时有功功率偏差为0。这与图7 所示分析结果一致，再次说明了本文所提方法的有效性。

新能源发电、分布式电源常表现出波动性、随机性、无法预测等特征，很难实现其自主协调控制。当风速、光照变化或储能调节时，虚拟同步机给定的参考有功功率需要做出调整。此时，虚拟同步机实际输出的有功功率Pe将产生明显的震荡和超调。当负荷突增或电网故障时，虚拟同步机也会在提升频率稳定性的同时不可避免地引起功率振荡问题[11]。

因此，引入本文所提方法可以有效抑制有功功率的振荡，提高有功功率的动态响应性能，能很好地解决有功功率动态震荡和稳态静差之间的矛盾问题，并且适用于直流侧配置铅酸、锂电等的储能变换器并网运行场景以及包含此类储能变换器的微电网接入配网场景。

3 仿真验证

为了验证本文所提基于阻尼功率调整的虚拟同步机有功功率控制方法的有效性，本文基于Matlab/Simulink 建立了所提方法的仿真模型，并进行了仿真验证。仿真所用参数如表1 所示，参考文献[11]，设置仿真工况如表2 所示。

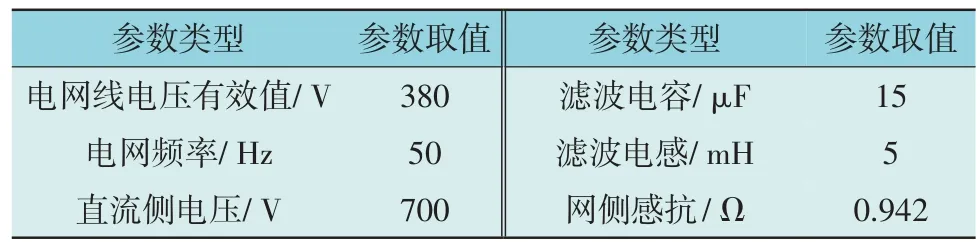
表1 仿真参数Table 1 Simulation parameters

表2 仿真工况Table 2 Simulation condition

图8 给出了D为0，8 和15 时常规方法虚拟同步机输出有功功率和频率的仿真结果。由图8（a）可见，在D=0、参考有功功率Pref突变时，虚拟同步机实际输出的有功功率Pe产生了明显的震荡和超调。随着D的逐渐增大，Pe的震荡和超调得到明显抑制。同时，由图8（b）可见，当D较小时，虚拟同步机实际输出的角频率ω也存在明显的震荡和超调，且该震荡和超调也随着D的增大而减小。可见，增大D可以显著提高系统的阻尼。然而，当电网频率出现偏差时，由图8（a）可见，随着D的逐渐增大，有功功率偏差也显著增大了。可见，增大D虽然可以抑制有功功率参考值变化时的功率震荡，但也会增大电网频率偏移时的有功功率偏差。这与理论分析一致，体现了常规方法的主要缺点。

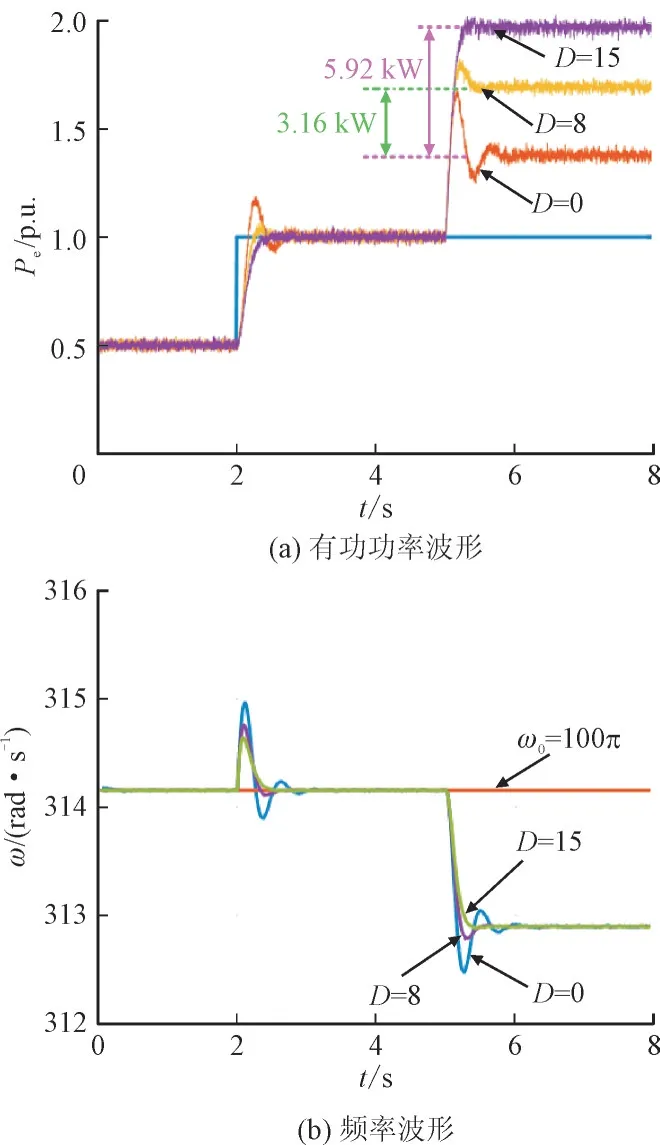
图8 D变化时常规有功功率和频率控制方法仿真结果Fig.8 Simulation results of output active power and frequency when D changes by conventional active power control method

图9 给出了D为0，8 和15 时本文所提方法虚拟同步机输出有功功率和频率的仿真结果。仿真时，取kP=0.001，kI=0.02。其他仿真条件与图8 相同。

图9 D变化时所提有功功率和频率控制方法仿真结果Fig.9 Simulation results of output active power and frequency`when D changes by the proposed active power control method

由图9 可见，当采用本文所提基于阻尼功率调整的虚拟同步机有功功率控制方法时，在D=0 时，有功功率和频率也存在明显的震荡和超调。然而，随着D的增大，有功功率和频率的震荡和超调均得到明显抑制。这与图6（c）分析结果一致。与此同时，在电网频率出现偏差时，由图9（a）可见，本文所提方法在D为8 和15 时，其有功功率偏差均为零。这与图7 分析结果一致。

为了进一步验证所提方法的有效性，与文献[11]所提方法进行了对比研究。图10 给出了文献[11]所提暂态前馈补偿（Feedforward Compensation，FFC）策略（补偿系数KFF=19.5，滞后时间常数τFF=0.006）与D=15 时本文所提方法虚拟同步机输出有功功率和频率的仿真结果。其他仿真条件与图9 相同。

图10 不同方法仿真结果对比Fig.10 Comparison of simulation results between different methods

由图10 可见，当参考有功功率Pref突变时，文献[11]所提FFC 策略与本文所提方法均能实现有功功率和频率的震荡和超调抑制。然而，FFC 策略的频率过冲比较明显，且功率和频率的纹波较大。这主要是FFC 策略需要使用微分运算的缘故。微分运算不可避免地会放大噪声的影响，影响系统的稳态性能和稳定性。与FFC 策略相比，本文所提方法采用比例积分控制器对阻尼功率进行调整，且积分控制器具有低通滤波功能，因此，本文所提方法的有功功率与频率的高频纹波较小。

由此可见，本文所提方法通过选择合适的D，kP和kI，既可以增大系统对有功功率的阻尼，减小有功功率的震荡和超调，又可以消除电网频率出现偏差时带来的有功功率稳态偏差问题，且具有更小的功率和频率纹波。因此，本文所提方法很好地解决了常规虚拟同步机存在的有功功率动态震荡、超调和稳态偏差之间的矛盾问题。仿真结果验证了本文所提方法及其理论分析的正确性和优越性。

4 结论

为了解决常规虚拟同步机控制存在的有功功率动态震荡和稳态偏差之间的矛盾问题，本文提出了一种基于阻尼功率比例积分调整的虚拟同步机有功功率控制策略。基于系统的闭环传递函数详细对比分析了常规方法的缺点和所提方法的优点，并通过单位阶跃响应分析选择了合适的控制参数。Matlab/Simulink 对比仿真结果表明，本文所提方法既可以显著减小有功功率参考值突变时的功率震荡和超调，又可以消除电网频率偏移时的有功功率稳态偏差，很好地解决了常规方法存在的矛盾问题。