考虑绿证-碳交易的多虚拟电厂混合博弈优化调度

徐慧慧，田云飞，赵宇洋，柴 宜，方 茜，梁 宁

（1.国网甘肃省电力公司经济技术研究院，甘肃兰州 730050；2.昆明理工大学电力工程学院，云南昆明 650500）

0 引言

“双碳”目标持续推进，如何实现电力系统能源高效利用，成为今后研究的重点之一。虚拟电厂（Virtual Power Plant，VPP）融合能源供给和能源消费，耦合分布式新能源、储能及多种负载，聚合产消者接入电力系统，能够充分挖掘需求侧的灵活性，提升能源利用率[1]。

随着VPP 及电力系统的发展，在同一电网下往往存在多个VPP 构成VPP 联盟。该联盟通过联盟成员间的点对点（Peer to Peer，P2P）能源交易，充分利用各个VPP 闲置资源[2-3]，减小对上级电网的依赖。

为突破传统单一主体优化方法存在一定的局限性，已有研究常通过博弈理论来处理P2P 能源交易的复杂关系。文献[4]构建了以多微网系统为领导者，负荷聚合商为跟随者的主从博弈优化调度模型，处理微网间电能交易问题。文献[5]提出多VPP 联合运行方式，在提升VPP 聚合体整体效益的同时降低对电网的依赖。文献[6]建立基于主从博弈的多主体投资多微网系统优化配置模型，平衡多微网间的收益。

主从博弈对于多VPP 系统内各子成员的P2P交易未进行详细考虑，无法得到主从博弈整体的最优效益[7]。而合作博弈能够兼顾全局利益，实现个体效益与整体效益最大化，提高参与者的交易积极性[8-9]。文献[10-11]建立多微网协同优化模型，通过考虑边际贡献度的Shapley 法对合作收益进行分配，但Shapley 法无法保证整体效益最大化。基于此，文献[12-13]基于纳什谈判理论构建多微网合作博弈模型，综合考虑参与者偏好及贡献度，对合作收益进行科学分配。

此外，在VPP 中纳入碳交易机制和绿证交易机制，能够减少VPP 碳排放量。文献[14-15]在源侧引入碳交易机制，优化源侧能源结构。文献[16-17]通过将碳交易成本纳入VPP 优化调度中，构建VPP低碳经济运行模型。文献[18]剖析了碳交易及绿证交易的机理，针对利益最大化的最优碳配额及绿证比例进行研究。文献[19]构建绿证-碳交易交互机制下电-气互联综合能源系统优化调度模型，提高风电消纳能力，显著减少碳排放。

文献[4-13]分析了主从博弈及合作博弈对参与者带来的效益，文献[14-19]考虑了绿证-碳交易机制对VPP 低碳转型促进作用。但还存在不足：一方面，联盟者只能被动接受领导者决策，联盟者与领导者无法进行有效互动；另一方面，固定电价影响联盟者参与需求响应和电能交互的积极性。

因此，本文提出一种电网运营商与VPP 联盟混合博弈优化模型，在电网运营商及VPP 联盟主从博弈中内嵌合作博弈，优化联盟向电网运营商的购售电价格和联盟成员间的电能交互价格，并使用纳什谈判理论分配联盟合作收益，将其等效成联盟效益最大化和合作收益分配2 个子问题。为提高求解效率，本文将二分法与交替方向乘子法（Alternating Direction Multiplier Method，ADMM）相结合求解混合博弈模型，并通过算例仿真验证了该方法可行性与有效性。

1 混合博弈优化框架

本文构建了电网运营商与VPP 联盟混合博弈优化框架，如图1 所示。

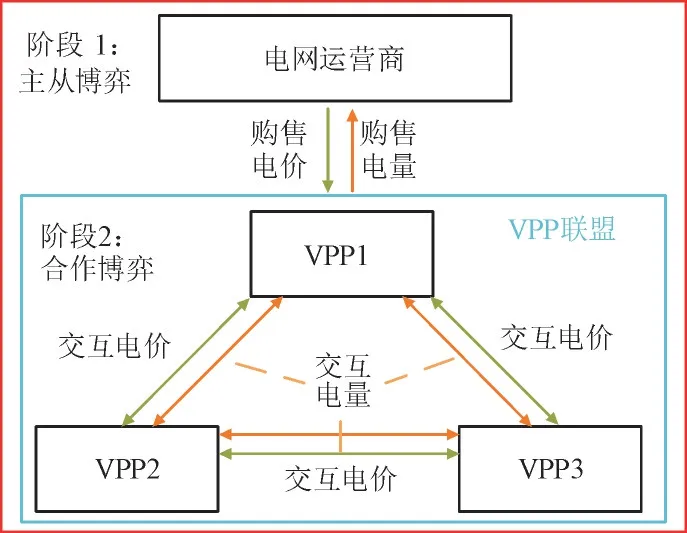
图1 混合博弈优化框架Fig.1 Optimization framework of mixed game

该混合博弈分为2 个阶段：阶段1 为电网运营商与VPP 联盟的主从博弈。电网运营商根据VPP联盟所提供的购售电需求调节交易价格，通过电网电价和上网电价与主电网交易，通过差价赚取利益，并将所制定的购能价格传递至阶段2；阶段2 为VPP 联盟成员之间的合作博弈。基于阶段1 的交易价格，多个VPP 合作组成VPP 联盟，各VPP 在合作效益最大化时得出最优的交易电量与交易价格，并将向电网运营商的购售电量传递至阶段1。当联盟成员电能富余时，可通过联盟间电能交易将富余电能售卖给联盟内部电能不足成员，剩余的电能以售电价格出售给电网运营商；反之则可购买联盟内其他成员的电能，不足的电能以购电价格向电网运营商购买。

VPP 整体框架如图2 所示。

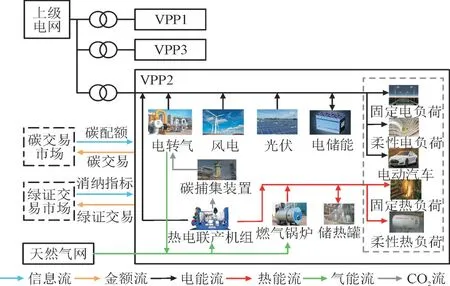
图2 VPP整体框架Fig.2 Overall framework of VPP

VPP 与上级电网相连，VPP 充分调用内部设备实现多能互补，减少对上级电网依赖。VPP 并与外部碳市场、绿证市场进行交易，通过碳捕捉及封存（Carbon Capture Storage，CCS）装置、碳排放约束以及绿证消纳指标提升VPP 低碳性。以VPP2 为例，VPP 中设备主要包括风电机组（Wind Turbine，WT）、光伏机组（Photovoltaic，PV）、热电联产机组（Combined Heat and Power，CHP）、燃气锅炉（Gas Boiler，GB）、电储能（Electrical Energy Storage，EES）和储热罐（Thermal Energy Storage，TES）。其中，VPP2 装配含P2G-CCS 装置的CHP，P2G-CCS 收集CHP 所排放的CO2制气，供给CHP 和GB 使用。VPP 协调多种设备出力满足内部能源需求，通过能源耦合设备实现能量间的转换，并引导需求侧柔性负荷进行需求响应（Demand Respond，DR）。

2 混合博弈优化模型

2.1 电网运营商与VPP联盟主从博弈

2.1.1 博弈领导者

电网运营商为主从博弈领导者，依据VPP 联盟的购售电量，制定VPP 联盟的购售电价格。

1）目标函数。电网运营商以自身效益FDSO最大化为目标，包括与电网及VPP 联盟进行电量交易的成本与收益。

其中，VPP 联盟购售电量为：

2）约束条件。电网运营商制定的购售电价应在一定区间内：

电网运营商为最大化自身效益，会将联盟购电价格设为最高，联盟售电价格设为最低。为避免此种问题，设定联盟购售电价格平均值约束：

2.1.2 博弈跟随者

VPP 联盟作为博弈的跟随者，依据电网运营商制定的购售电价格，优化得到联盟的购售电量、自身调度方案和VPP 间交易电量，并将购售电量反馈给电网运营商。

1）目标函数。VPP 联盟成员以最小化自身成本FVPPi为目标，目标函数包括购售电成本、VPP 间交互成本、燃气成本、需求响应成本和储能运维成本。

2）约束条件。

（1）P2P 电能交易约束为：

（2）需求响应约束为：

WT，PV，储能、CHP 及GB 约束详见文献[20-21]，电动汽车约束详见文献[22]。

（3）功率平衡约束为：

式中：Nevd，Nevc分别为放电、充电的电动汽车数量；分别为t时刻VPPi第n辆电动汽车放电、充电量。

2.2 VPP联盟纳什谈判模型

VPP 联盟通过合作对电网运营商的决策进行响应，合作目标为整体效益最大化。VPP 联盟纳什谈判模型为：

式中：Fi为VPPi参与谈判获得的效益；为VPPi未参与谈判获得的效益。

VPP 纳什谈判模型为多变量耦合的非凸非线性问题[23]，因此将模型转换为VPP 联盟成本最小化子问题（P1）和收益分配子问题（P2），依次求解。

子问题（P1）：VPP 联盟成本最小化。

子问题（P2）：合作收益分配。

式中：FVPPi*为子问题P1 中求得的VPPi效益；，分别为子问题P1 中求得的t时刻购售电价。

3 混合博弈模型求解

本文的混合博弈模型求解流程如图3 所示，其中，k，d分别为阶段1 和阶段2 循环次数。阶段1为主从博弈，通过二分法进行循环迭代并得到电网运营商制定的购售电价格、VPP 与电网的购售电量、VPP 联盟内部出力结果和VPP 间电能交易电量，并将求解结果输入阶段2。阶段2 为联盟间的合作博弈，通过ADMM 求解VPP 间电能交易价格。

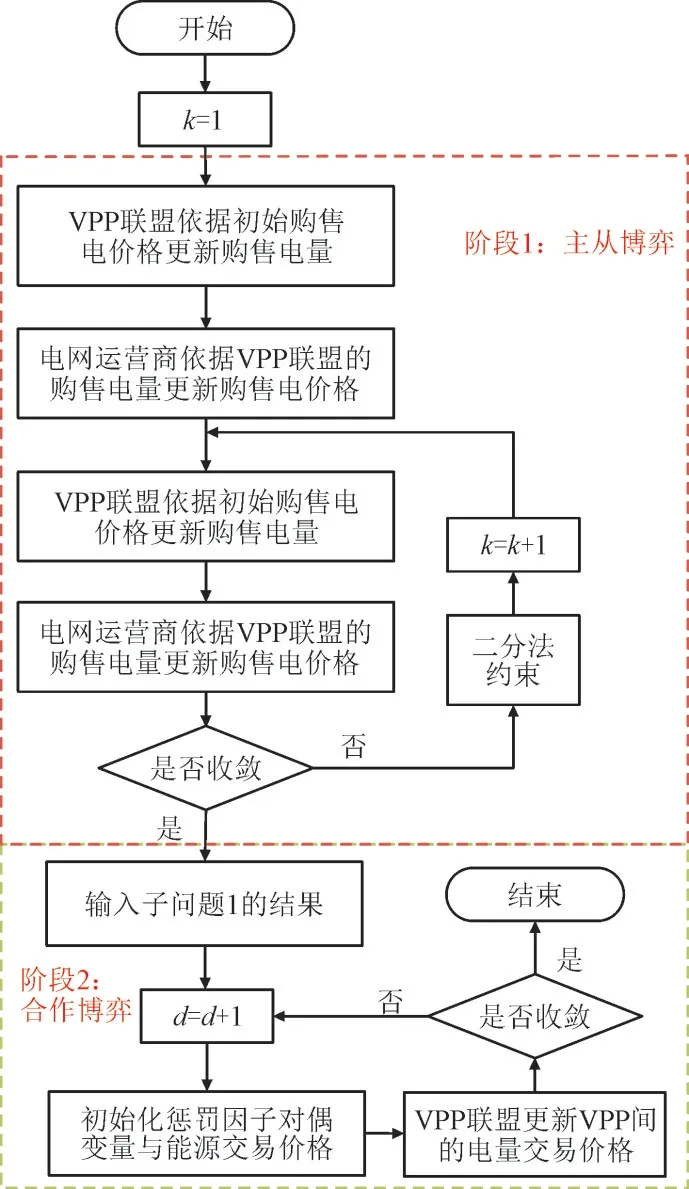
图3 求解流程Fig.3 Solving procedure for the proposed mixed game model

4 算例分析

4.1 参数设置

以某地区为例，考虑电网运营商与3 个VPP 间的混合博弈，各VPP 新能源出力及电热负荷量参考文献[24]。VPP1 和VPP3 为常规CHP 机组，VPP2 为改进的含CCS-P2G 的CHP 机组。设置碳交易基准价格为50 元／t，初始碳配额系数为0.75 t/MWh[25]，ADMM 收敛系数为0.001[26]。

4.2 场景对比分析

4.2.1 不同场景下运行成本分析

为分析本文所提模型的有效性，设置以下5 个场景：场景1，考虑主从博弈及合作博弈，参与绿证-碳交易市场，即本文所提方法；场景2，考虑主从博弈，不考虑合作博弈，参与绿证-碳交易市场；场景3，考虑主从博弈及合作博弈，不参与绿证-碳交易市场；场景4，考虑主从博弈，不考虑合作博弈，不参与绿证-碳交易市场；场景5，不考虑主从博弈，考虑合作博弈，参与绿证-碳交易市场。

5 种场景下VPP 各项成本如表1 所示。VPP合作前后成本如表2 所示。

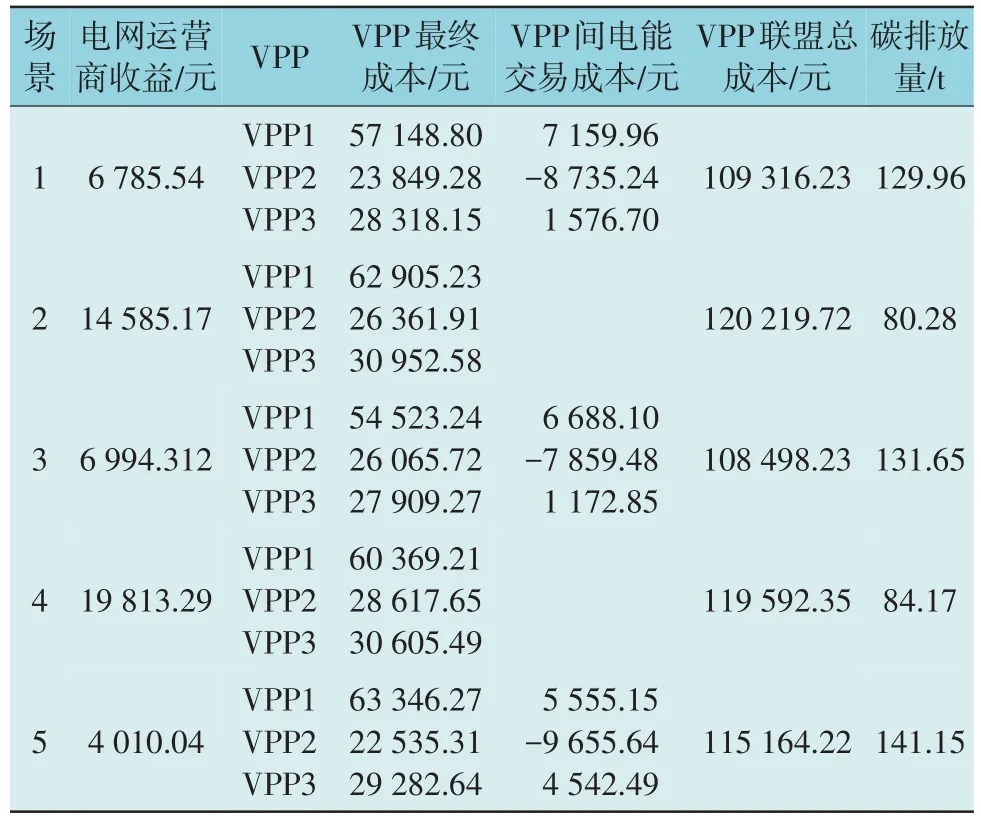
表1 不同场景下运行结果对比Table 1 Comparison of operation results among different scenarios

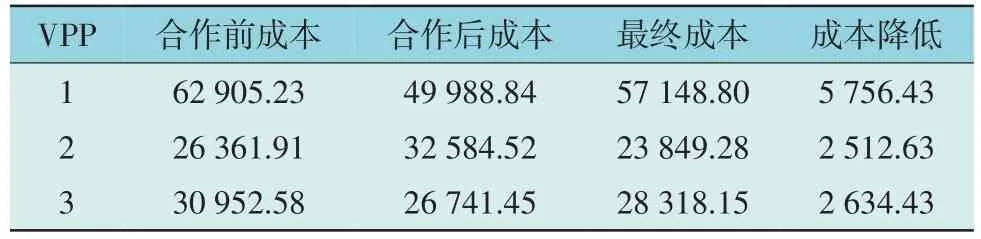
表2 VPP合作前后成本对比Table 2 Cost comparison of VPP before and after cooperation 元

通过表1 中场景1 和2 可以看出，场景1 考虑了多VPP 间合作博弈后，VPP 联盟总成本降低了10 903.49 元，电网运营商收益下降了7 799.63 元，这是因为VPP 间通过P2P 电能交易，降低了对电网运营商依赖程度，而电网运营商效益也随之降低。此外，对比场景1 和5 可以看出，场景1 考虑混合博弈后，电网运营商发布给VPP 联盟的价格产生浮动变化，VPP 可灵活调整购售电时间，VPP 联盟的总成本降低了5 847.99 元，电网运营商收益下降了2 775.50 元。

由表2 可知，各VPP 联盟成员最终成本分别降低了5 756.43 元，2 512.63 元，2 634.43 元，这是因为引入纳什谈判理论后，能够在降低VPP 联盟总成本的同时，降低各VPP 的成本，保证合作参与者的利益，合理分配合作效益。

对比表1 中场景1 和3 以及场景2 和4 可知，由于场景3 和4 未参与绿证-碳交易市场，其成本较场景1 和2 低，但同时由于缺少碳排放约束，场景3 和4 的碳排放量均比场景1 和2 高，且场景3中VPP 间电量交互效益不如场景1 好。由此可以看出，参与绿证-碳交易市场，尽管提高了VPP 部分成本，但同时也能降低碳排放量，提升VPP 联盟低碳性和交互性。

此外，对比场景1 和2 以及场景3 和4 可以看出，VPP 参与合作博弈后，为在博弈中实现利益最大化，各VPP 调用自身设备，发出更多的电力、热力，减少向上级购电，增加VPP 间的交互。这样虽然减小了VPP 总成本，但也在一定程度上增加了碳排放量。

4.2.2 不同场景下优化结果分析

场景1 与场景2 的主从博弈电价优化对比结果如图4 所示。从图4 可以看出，场景1 的购电价格低于场景2，场景1 除17:00—19:00 时段电能价格设定较高外，VPP 联盟向电网运营商的购电价格基本接近上限值。这是由于场景1 考虑VPP 间的合作博弈，各VPP 有新的购电渠道，对电网运营商的依赖程度下降，与电网运营商的议价能力更强。

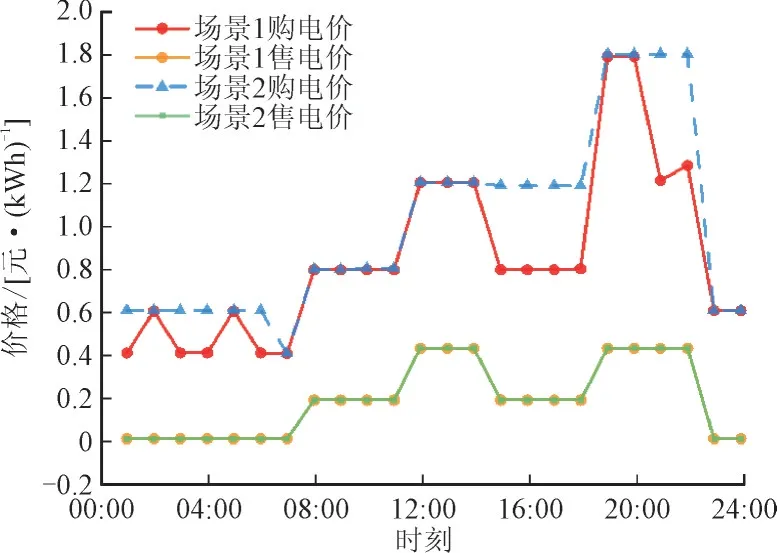
图4 场景1和场景2主从博弈电价曲线对比Fig.4 Comparison of electricity price curves for masterslave game in scenario1 and scenario 2

场景1 和场景2 中VPP 购电量结果对比如表3 所示。由表3 可知，场景1 考虑了VPP 间合作博弈，VPP 购电总量降低了16 506.30 kWh，原本购电量较低的VPP2 购电量提升了1 049.84 kWh，原本购电量较高的VPP1 和VPP3 购电量分别降低了14 544.94 kWh，2 911.21 kWh，充分说明合作博弈可有效降低VPP 联盟对电网运营商购电依赖程度，提高VPP 间交互性。

表3 场景1和场景2中VPP购电量结果对比Table 3 Comparison of purchasing power of VPP in scenario1 and scenario2 kWh

4.3 交易结果分析

本文阶段2 制定VPP 联盟成员间的交易电价，优化结果如图5 所示。从图5 可以看出，为了保证VPP 联盟合作的利益，VPP 制定的交易价格需限制在阶段1 所制定的购售电价内，因此各VPP 成员能够通过VPP 间的交易进行合作，与上级电网运营商进行议价。

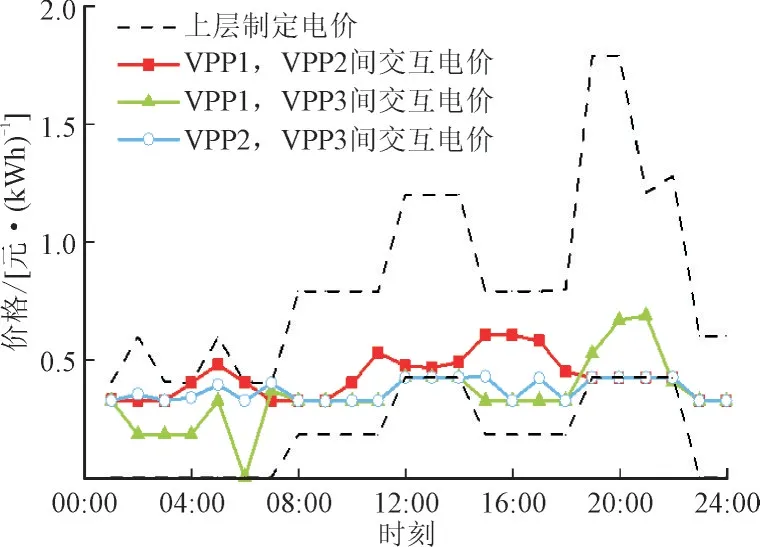
图5 VPP间交互电价曲线图Fig.5 Curves for interactive electricity price between VPPs

以VPP2 为例，VPP2 出力结果如图6 所示。VPP2 自身电量较为富余，在00:00—06:00，09:00—18:00 时段出售电能给VPP1，在20：00—22:00 时段出售电能给VPP3，在07:00—16:00 时段内向电网运营商出售电能获取利润，仅在23：00—24：00 向上级购电。在00:00—11:00 及15:00—24:00 时段内进行需求响应，转移用电负荷，并在5：00—19：00时段引导电动汽车进行放电，降低用电压力。

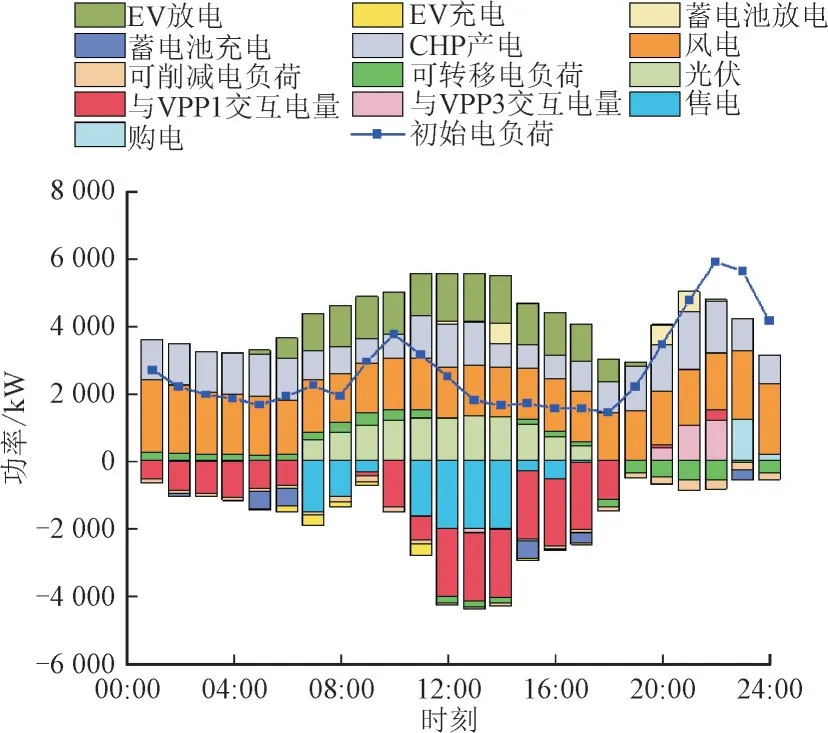
图6 VPP2电能供需平衡图Fig.6 Diagram showing power balance of VPP2 between supply and demand

5 结论

为充分挖掘VPP 间的合作潜力，本文提出了考虑绿证-碳交易的多VPP 混合博弈优化调度框架，构建电网运营商与VPP 联盟的主从博弈模型及VPP 成员间的合作博弈模型。通过分析得到以下结论：

1）本文通过二分法结合ADMM 算法求解多VPP 混合博弈优化调度模型能够有效迭代收敛，各VPP 在合作博弈的过程中，仅交换电量交易及交易电价信息，能够有效保护各交易主体的隐私。

2）通过博弈理论制定电网运营商与VPP 联盟间的购售电价及VPP 间的交互电价，可提升各VPP间交互性，降低VPP 联盟总成本及各成员的成本，实现VPP 联盟的高效合作及收益的合理分配。

3）相比于不考虑绿证-碳交易，各VPP 参与绿证-碳交易后，总成本有所提升，但同时降低了VPP的碳排放量，提升了VPP 间的交互程度，降低VPP联盟对电网的依赖。