Saddlepoint Approximation Method in Reliability Analysis:A Review

Debiao Meng ,Yipeng Guo ,Yihe Xu ,Shiyuan Yang ,Yongqiang Guo ,Lidong Pan and Xinkai Guo

1School of Mechanical and Electrical Engineering,University of Electronic Science and Technology of China,Chengdu,611731,China

2Institute of Electronic and Information Engineering of UESTC in Guangdong,Dongguan,523808,China

3Glasgow College,University of Electronic Science and Technology of China,Chengdu,611731,China

4Beijing Research Institute of Mechanical&Electrical Technology,Ltd.,Beijing,100083,China

ABSTRACT The escalating need for reliability analysis (RA) and reliability-based design optimization (RBDO) within engineering challenges has prompted the advancement of saddlepoint approximation methods(SAM)tailored for such problems.This article offers a detailed overview of the general SAM and summarizes the method characteristics first.Subsequently,recent enhancements in the SAM theoretical framework are assessed.Notably,the mean value first-order saddlepoint approximation(MVFOSA) bears resemblance to the conceptual framework of the mean value second-order saddlepoint approximation(MVSOSA);the latter serves as an auxiliary approach to the former.Their distinction is rooted in the varying expansion orders of the performance function as implemented through the Taylor method.Both the saddlepoint approximation and third-moment(SATM)and saddlepoint approximation and fourth-moment(SAFM)strategies model the cumulant generating function(CGF)by leveraging the initial random moments of the function.Although their optimal application domains diverge,each method consistently ensures superior relative precision,enhanced efficiency,and sustained stability.Every method elucidated is exemplified through pertinent RA or RBDO scenarios.By juxtaposing them against alternative strategies,the efficacy of these methods becomes evident.The outcomes proffered are subsequently employed as a foundation for contemplating prospective theoretical and practical research endeavors concerning SAMs.The main purpose and value of this article is to review the SAM and reliability-related issues,which can provide some reference and inspiration for future research scholars in this field.

KEYWORDS Reliability analysis;reliability-based design optimization;saddlepoint approximation

1 Introduction

A saddlepoint refers to a stationary point of a non-local extreme point,which is a singular point that is stable in one direction and unstable in the other direction [1].The curves,surfaces,or hypersurfaces of the saddlepoint neighborhood of a smooth function are all located on different sides of the tangent to the saddlepoint.Fig.1 illustrates a typical example of a saddlepoint.

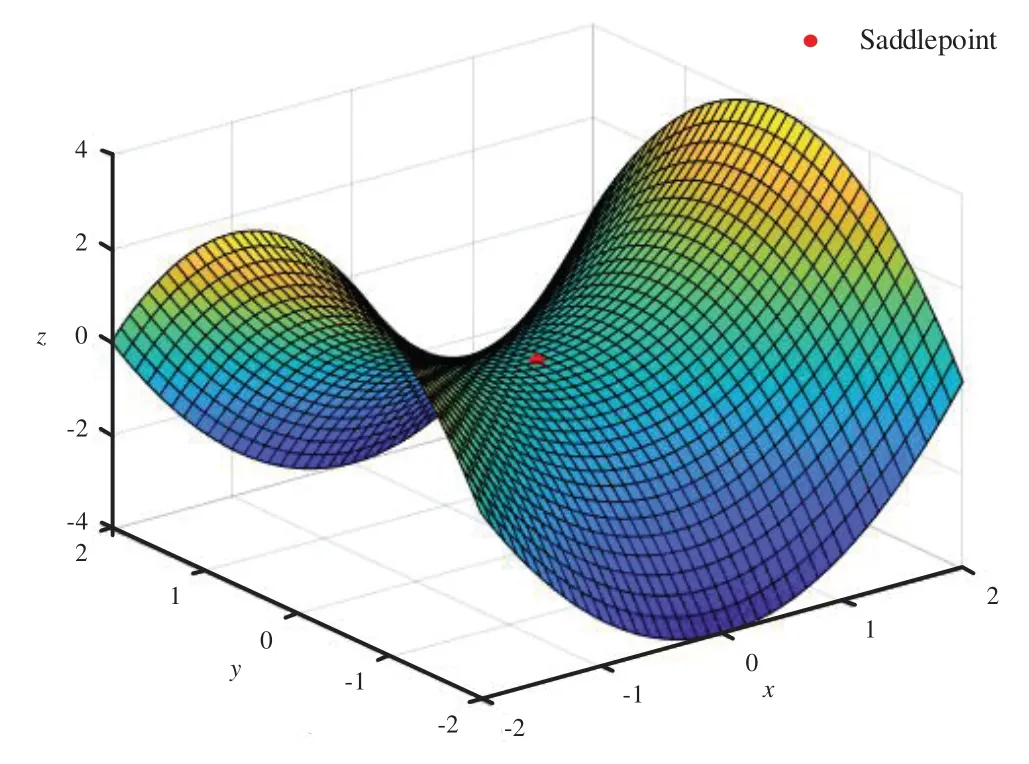
Figure 1:Example diagram of saddlepoint

Saddlepoint approximation arises from the approximate statistics of the probability density function (PDF) and cumulative distribution function (CDF),particularly the latter [2,3].It stands as a potent method among various integral approximation techniques,offering distinct advantages of a straightforward formula,swift computation,and effective approximation.Even in the presence of a limited sample size,the saddlepoint approximation method(SAM)largely meets application demands[4–8].Throughout history,numerous scholars have explored and propelled the advancement of SAM[9–13].Hu et al.[14] introduced a saddlepoint approximation technique for reliability assessment,eliminating the need for additional transformations and approximations to the quadratic function.As saddlepoint approximation continues to evolve,it finds extensive utility in both physics and practical engineering fields[15–19].SAM has been instrumental in developing approximate solutions for robust convex optimization,leading to more resilient and efficient design strategies in engineering [20].Its applications extend to queueing theory,insurance mathematics and statistics [21–23].In the area of computational mechanics,the stabilized extended finite elements method for saddlepoint problems has proven effective for handling unfitted interfaces,enhancing the computational simulation of physical phenomena[24].

Particularly in reliability analysis (RA) and reliability-based design optimization (RBDO)domains,SAM can provide an important support.Yuan et al.[25] introduced a reliability-based multidisciplinary design optimization that combines saddlepoint approximation and third-moment techniques.Fig.2 depicts the basic flow chart of RA using SAM in engineering.

The concept of reliability emerged in the 19th century,aligning with the advancements of the Industrial Revolution.The growing momentum of this era demanded a quantitative approach to reliability,specifically in factory production and the execution of engineering projects [26,27].Consequently,reliability became an established integral discipline in engineering.

Letf(x)=0 be the true limit-state equation,withβrepresenting the reliability,indicating the distance from the origin to the hyperplane in the standard normal space;then,the geometric representation of reliability andβcan be expressed as in Fig.3.

Figure 2:RA based on SAM in engineering

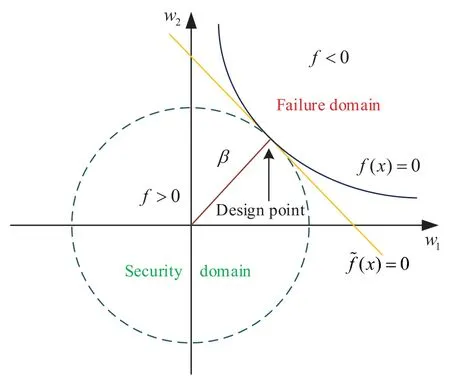
Figure 3:Geometric representation of reliability and β

Numerous researchers have extensively investigated and formulated various reliability methods tailored for practical engineering applications [28–32].Relevant progress has been made in optimization and estimation strategies for system reliability assignment problems,demonstrating the importance of optimization methods in reliability engineering [33–36].Machine learning-based methods are becoming increasingly influential in structural reliability analysis,offering new tools and perspectives for tackling reliability problems[37–40].RA has been further developed in the following specific branches,including foundational and advanced techniques in moment methods for structural reliability [41–45],computational techniques and machine learning in structural reliability [46–50],time-dependent aspects and non-probabilistic approaches in RA [51–55] and human factors and adaptive techniques in RA[56–60].

RA also holds significant importance in ensuring the smooth operation of entire projects across diverse engineering fields [61–65].It plays a cornerstone role in the fields [66–70].Scholars have developed related techniques for fault diagnosis[71]and studied that dynamic and time-varying RA can predict system lifetime under fluctuating conditions [72–76].This is critical for uninterrupted infrastructure functionality[77–81].RA also has important analysis and reference significance for the sustained performance of power systems and modern technologies[82–85].Moreover,the integration of machine learning stands out as one of the primary developmental directions in RA[86–90].Fig.4 illustrates the main categories within RA methods,and Fig.5 depicts the primary categories in approximation methods.

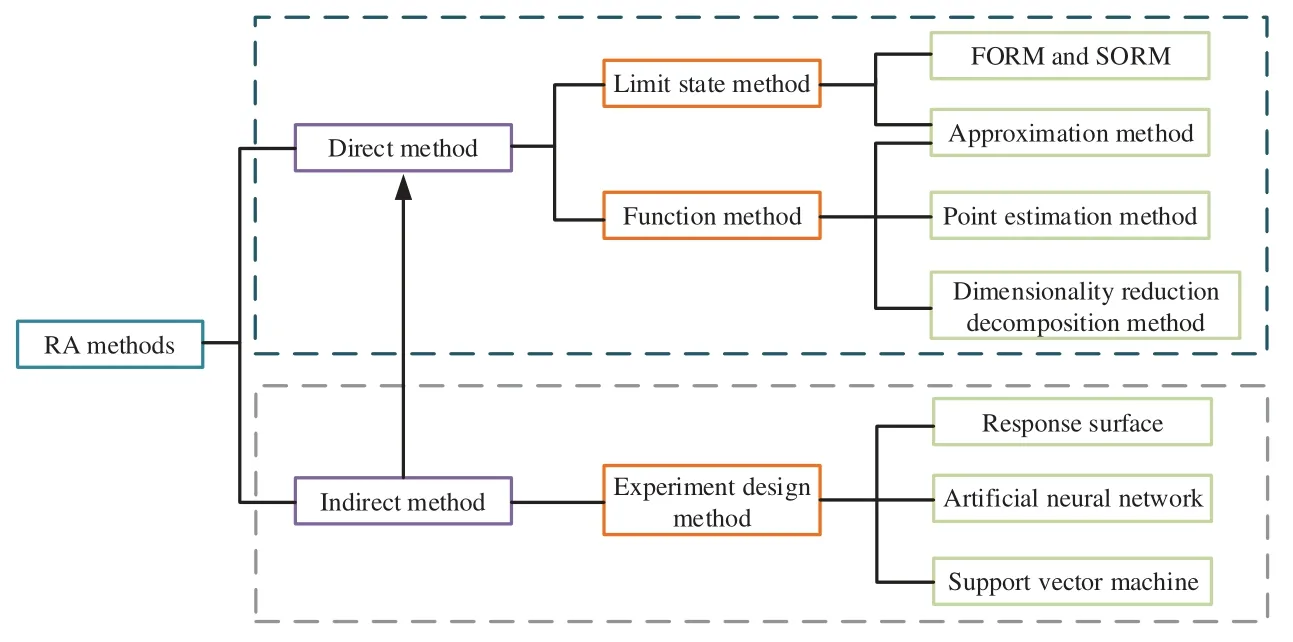
Figure 4:Categories of RA

Figure 5:Categories of approximation in RA

The first-order reliability method(FORM)is one of the crucial and commonly utilized approaches within most probable point(MPP)-based methods[15].Its fundamental logic involves approximating the actual limit-state function with a plane at the MPP,which occurs on the limit-state surface closest to the origin in the standard normal space[91,92].FORM offers the advantage of effectively balancing efficiency and accuracy[93–95].Shin and Lee used FORM to evaluate the accident probability and conducted numerical studies using a single truck model,and obtained results that met the given goals[96].According to the characteristics of FORM,its fusion with uncertainty analysis yields significant benefits,leading to the development of related methods[97–100].Additionally,FORM is also widely used in RA across various fields[101–105].Many researchers focused on enhancing the stability and accuracy of FORM in RA,including innovative methods to control numerical instabilities and update failure points [106–110].They also provided comparative analyses,theoretical insights,and reviews of FORM within the broader context of reliability methods [111–114].Advanced integration and optimization of FORM are important future development directions for this method[115–118].

However,FORM overlooks the nonlinearity of the original limit-state function,often resulting in substantial errors in many cases.To address this,the second-order reliability method (SORM) was introduced.SORM involves a quadratic expansion of the limit-state function at the point nearest to the origin in the standard normal coordinate system.By considering the nonlinearity,SORM approximates the limit-state function using a parabolic surface,providing more accurate reliability calculations than FORM[119].Consequently,SORM commonly utilizes a parabolic approximation of the fitted quadratic polynomial surface and its related theories have been well developed [120–123].Many related efficient and improved algorithms have been proposed [124–127].Some novel approximation and extension methods are also used to enhance SORM [128–132].As an advanced iteration of FORM,SORM is also widely used in engineering.The main areas included are geotechnical engineering and underground structures[133–136],advanced SORM techniques and sensitivity analysis[137–140],design optimization of structures[141–144],RA in mechanical and fatigue analysis[145–147].Scholars have proven its effectiveness by comparing FORM/SORM with other methods[148,149].Fig.6 illustrates the basic principles and distinctions between FORM and SORM.

Figure 6:Basic principles of FORM and SORM

In the context of RA,there are many analysis methods that are closely related to saddlepoint approximation [150–152].Although FORM is commonly applied in RA,its limitations in handling inaccurate situations for nonlinear problems have prompted the introduction of the SAM,which offers improved solutions [153].The utilization of second-order saddlepoint approximation (SOSA)in component RA has demonstrated enhanced accuracy compared with the traditional SORM[154].

Reliability metrics have led to advancements in RBDO methods[155–157].Approximate model technology has important applications in RBDO [158,159].Many scholars have developed RBDO by integrating novel algorithms [160–163].Liu et al.developed a Multi-objective RBDO based on probability and interval hybrid model [164].Meng et al.proposed a general fidelity transformation framework for RBDO with arbitrary precision [165].Product reliability design optimization aims to achieve optimal design probabilistically,utilizing product reliability as either a constraint or an objective and employing appropriate optimization techniques.The effectiveness of RBDO serves as a critical metric to assess its real-world applicability[166].However,a prevalent challenge across various RBDO methodologies is their substantial computational demand[167–169].In this regard,relevant scholars have also proposed some Efficient and Robust RBDO Methods[170–172].Integrating SAM with RBDO analysis allows for mitigating this issue.Consequently,the fusion of SAM and RBDO has garnered significant attention in academic investigations [173,174].Fig.7 illustrates the relationship between reliability analysis and optimization.Moreover,other theoretical methods apply to RA[175–177].

This article offers an overview of the utilization and progression of SAMs in RA and RBDO.It can serve as a valuable reference and guide for subsequent research in this domain.The article is structured into five sections.The second section presents the fundamental algorithmic logic of the general SAM.The third section presents the core algorithmic logic and distinct features of recently enhanced SAMs.The fourth section discusses the application and performance of various SAMs in RA and RBDO engineering examples,summarizing the merits of each approach.Finally,the last section presents analytical conclusions and outlines potential directions for future studies.

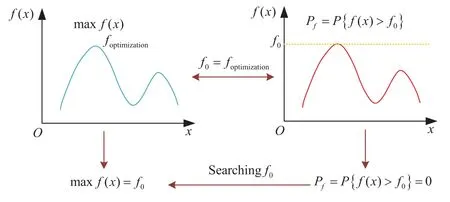
Figure 7:Relationship between reliability analysis and optimization

2 General SAM

SAM is an effective approximation tool,particularly suited for tackling high-dimensional integration challenges.This section introduces the general process of SAM.Its fundamental logic lies in obtaining the cumulant generating function (CGF) of a random variable,which enables approximations of the associated CDF and PDF.Calculating CDFs and PDFs is a crucial aspect of engineering analysis.Therefore,the primary objective of the general SAM is to facilitate more convenient computations of CDFs and PDFs.

Table 1 presents some common distributions of CGFs[178].

Table 1:CGFs of some common distributions

Letf(xR)be the PDF of the random variableXR;then,the moment-generating function(MGF)ofXRis denoted as:

The CGF ofXRis expressed as:

ForXR,the approximation of the PDF ofXRcan be expressed using saddlepoint approximation:

Letϕ(·)andΦ(·)be the standard normal distributions of the PDF and CDF,respectively.Generally,the failure probabilitycan be denoted as:

wherewis the solution of Eq.(6):

andvis the solution of Eq.(7):

According to the linear relationship above,the CGFs ofcan be expressed in terms ofG:

The approximation of the CDF ofGcan be solved using Eqs.(4)–(8).can be calculated using Eq.(11):

This section offers a comprehensive review of the conventional SAM.The resultant equations are highly nonlinear,and the CGFs ofXRjare essential to approximate the CDF ofG.These limitations may confine the application of SAMs within engineering contexts.Therefore,there exists a pressing need to enhance this method to increase its practical value.

3 Improved SAMs

The general SAM features limitations in its application.Utilizing SAM necessitates acquiring the saddlepoint equation,which relies on tractable variables having existing CGFs.In cases in which CGFs are nonexistent,the general SAM cannot be applied.Additionally,for most probability distribution types,the corresponding CGFs tend to be complex,leading to potentially highly nonlinear saddlepoint equations[174].These factors restrict SAM utilization.To enhance the efficiency and accuracy of SAM and address the shortcomings of the traditional approach,several scholars have introduced improvements and demonstrated the effectiveness of these methods in practical engineering applications.Fig.8 depicts numerous reliability analysis methods based on saddlepoint approximation.This article introduces four of these methods in detail.They are mean value firstorder saddlepoint approximation(MVFOSA),mean value second-order saddlepoint approximation(MVSOSA),saddlepoint approximation and third-moment(SATM)and saddlepoint approximation and fourth-moment(SAFM).

Figure 8:Improved SAMs

3.1 MVFOSA

MVFOSA demonstrates efficiency and robustness comparable to those of the general SAM but offers superior accuracy.MVFOSA utilizes the first-order Taylor method to linearly expand the performance functionGwithin the original random space[178].

According to the abovementioned two properties,the CGF ofGcan be calculated using Eq.(13):

K′(t)is the first-order derivative of CGF;then,tsis the solution of Eq.(14):

When both the CGF ofGand the saddlepointtsare obtained,the CDF and PDF can be estimated via MVFOSA.

As previously highlighted,MVFOSA utilizes comprehensive distribution information,necessitating only a saddlepoint identification process.Owing to these characteristics,MVFOSA achieves enhanced accuracy.

3.2 MVSOSA

MVSOSA represents an alternative method to MVFOSA [179].The primary distinction lies in MVSOSA’s utilization of the mean values of random information as the point for the second-order Taylor expansionG(XR).It can be denoted as Eq.(15):

where XR=[X1,X2,X3,...,Xi]are the random variables,andμiis the corresponding mean value ofXi.

Eq.(15)is equivalent to Eq.(16):

Then,Ycan be expressed as:

With the assumption that the random design variables XRfollow a Gaussian distribution,μis the mean value of XRandσis the covariance of XR.The MGF ofYcan be expressed as Eq.(19):

According to the two properties of CGF mentioned in Section 3.1,the CGF ofYcan be calculated using Eq.(20):

Furthermore,the first derivative ofYis

and the second derivative ofYis

Then,the PDF ofYcan be calculated using Eq.(3).

MVSOSA can also provide higher accuracy than MVFOSA and can be applied in a wide range of practical projects.

3.3 SATM

SATM is a method developed from general saddlepoint approximation [25].The basic idea of SATM is introduced below.

WhenMG(t)exists,MG(0)is equal to 1,andis equal toE(Gl).means thelth derivative ofMG(t),l=1,2,3,...,n.

Therefore,the first three derivatives ofKG(t)are given as:

whereμGis the mean,is the standard deviation,andα3Gis the variance ofG.

In addition,the standardized form ofGcan be calculated asGS=.The transformation is linear,ensuring that the nonlinearity of the limit-state function does not increase.This transformation maintains numerical stability in practical engineering.Then,Eq.(24)can be obtained:

Considering that the challenges of solving the saddlepoint equation and obtaining the CGF may impact the utilization of the saddlepoint method,a simplified version of the CGFforGscan be formulated as follows:

whered1,d2,andd3are determined constants,andeis a prescribed value,which is usually given ase=.The derivatives ofcan be obtained using Eq.(26):

According to Eqs.(23)and(26),the following can be deduced:

If the value ofeis given,it will be simpler to obtainin SATM than in the conventional SAM.The PDF ofGScan be approximately expressed in terms of:

The CDF ofGSis similar to Eq.(4);it can be expressed as:

Furthermore,the PDF ofGcan be approximately obtained according to the linear relationship betweenGSandGas Eq.(33):

Then,the CDF ofGcan also be calculated using Eqs.(34)or(35):

According to the above equations,the CGF ofGcan be expressed as:

Then,the CDF ofGcan be expressed as:

As mentioned above,KG(t)can be obtained solely using the first three moments.Thus,SATM allows for the derivation of a CGF for a random variable following a specific distribution.

3.4 SAFM

In contrast to SATM,SAFM is an enhanced high-order moment-based SAM [180].According to Section 3.3 and Eq.(23),the fourth derivative ofKG(t)can be expressed as

whereη4Gdenotes the fourth central moment ofG.

According to SATM,Eq.(25) can be used to express the CGF in terms ofGS;then,the fourth derivative ofcan be obtained using Eq.(42):

Then,Eq.(43)can be obtained using Eqs.(23)and(41):

According to Eqs.(23),(41),and the saddlepoint equation-g=0,the saddlepoint equation can be expressed as:

According to Section 2,the saddlepoint approximation to the CDF ofGcan be expressed in the same form as Eq.(35).Consequently,the failure probability of the structure withGcan be expressed as:

Wheng=0,the failure probability of the random structure is estimated at the mean of the distribution ofG;the CDF can be expressed as:

Under the same condition,Eq.(51)can be applied as an alternative method to estimate the failure probability:

In SAFM,the first four stochastic moments form the foundation for approximating the CGF.Employing the general SAM enables the assessment of the failure probability in a random structure using the approximated CGF.Notably,SAFM offers enhanced accuracy compared with the conventional SAM.

4 Improved SAMs in Application

As previously mentioned,the demand for reliability in modern engineering design is constantly increasing.To provide readers with a better understanding of the specific engineering applications and the value of the aforementioned method,this section presents three engineering-related examples.These examples encompass all of the methods in Section 3,and some related methods are presented for comparison.The comparison within these engineering cases will highlight the effectiveness of the improved SAMs.

4.1 Reliability-Based Optimization for Offshore Structures

The wellhead platform represents an economical solution for offshore oilfield development,providing a provisional structure that safeguards the wellhead situated on the seabed.

In the given context,wave force-induced damage is the primary factor influencing RA.The core principle of RBDO involves constructing a probabilistic model to encapsulate inherent uncertainties in engineering structures.The RBDO methodology allows for addressing prevalent uncertainties in engineering applications,ensuring that the design aligns with the project’s specified reliability criteria.Fig.9 illustrates the concept diagram of the wellhead platform’s appearance,while Fig.10 offers a specific schematic.Table 2 presents the random design parameters in this case [179].According to the optimization results in Table 3,the optimized volume can be calculated.The minimum volume obtained through RBDO-MVSOSA calculation is 15.37 m3,which is 9%smaller than that obtained using the initial scheme,and it is the best result.These results indicate that RBDO with improved SAMs generates acceptable optimization schemes.Comparative data reveals that RBDO-MVSOSA tends to produce more conservative results than RBDO-MVFOSA,aligning closer with the results from RBDO-Monte Carlo simulation(MCS).

Table 2:Random design parameters in offshore structures

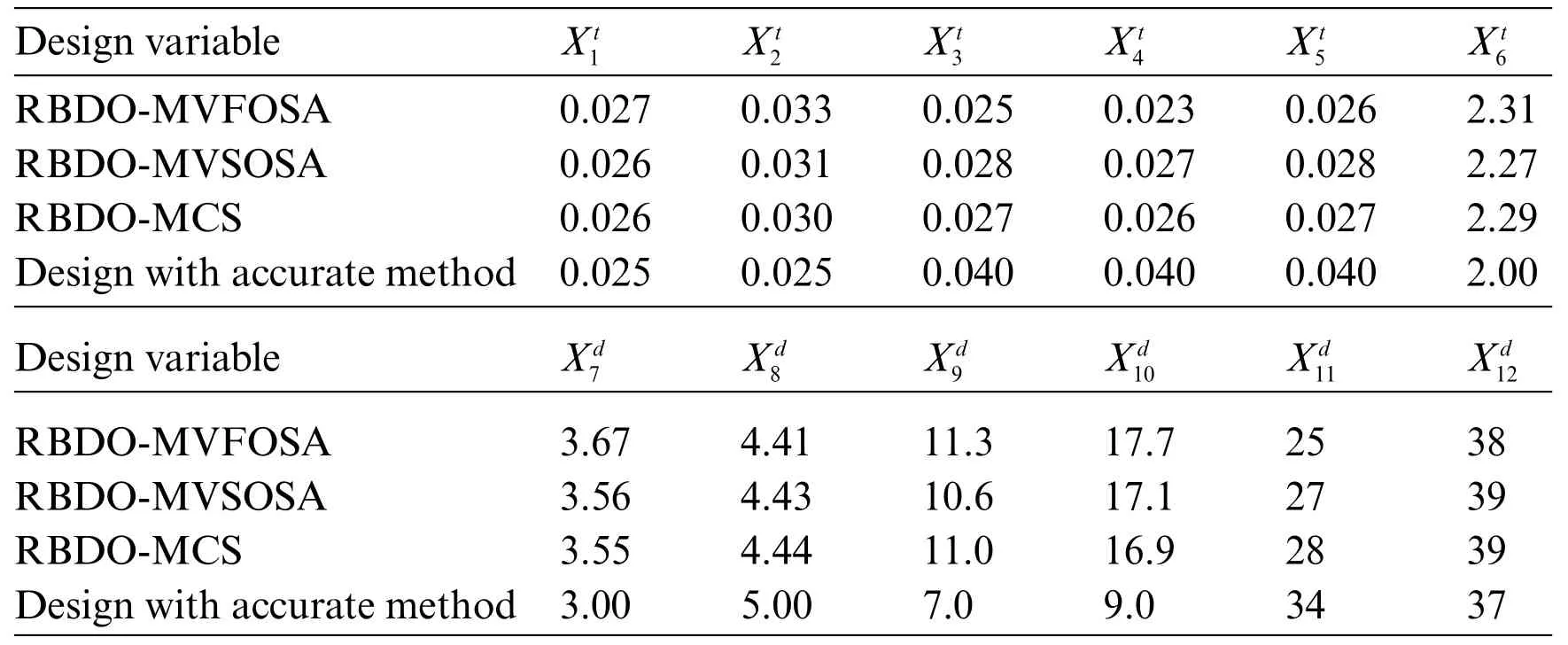
Table 3:Solutions of RBDO with different methods

This example demonstrates that RBDO-MVSOSA offers superior accuracy and that enhanced SAMs positively influence reliability-related issues.

4.2 Failure Probability Evaluation of Reinforced Concrete Beam

Reinforced concrete beams,pivotal load-bearing elements in engineering structures such as buildings and bridges,have widespread applications [181].Therefore,their reliability is paramount.Specific data for this example are available in reference[180].The schematic of a reinforced concrete beam is depicted in Fig.11.

The performance function of the concrete beam model can be expressed as Eq.(52):

whereSxrepresents the area of the reinforcing cross section,σxrepresents the steel yield strength,σpxrepresents the concrete compressive strength,andWrepresents the total moment produced by the load.The width and height of the beam ared=12 in andh=19 in,respectively.

Figure 9:Concept diagram of the wellhead platform

Figure 10:Illustration of a wellhead platform

Figure 11:Reinforced concrete beam

The distributions of input random variables are shown in Table 4:

Table 4:Distribution of input variables

The first four moments of the state variable are shown in Eq.(53):

The results of the failure probability estimate using the different improved SAMs and MCS are shown in Table 5.

Table 5:Results of RA

According to the aforementioned results,both SATM and SAFM offer failure probability estimates that closely align with the results of MCS.This suggests that the refined approximation methods employed in this study yield high precision.Fig.11 presents the comparison of estimated CDF tails derived from different techniques.

According to the results of the comparison,the closer the tail line in the figure is to MCS,the higher the accuracy of the method.According to the data in Fig.12,the CDF tail estimated by SAFM matches the results of MCS better than the CDF tail estimated by SATM,while SATM can also provide acceptable results.In Table 4,Pfdenotes the failure probability calculated by different methods.Compared with SATM,SAFM yieldsPfcloser to the MCS results.

This example demonstrates the high practicality of both SATM and SAFM in addressing reliability issues in engineering.

4.3 Reliability Evaluation of a Roof Structure

The schematic diagram of a typical roof structure in civil construction is shown in Fig.13,and its simplified force analysis diagram is shown in Fig.14.

Figure 12:Comparison of the CDF tails derived from different methods

Figure 13:Roof structure

Figure 14:Simplified force analysis of the roof structure

The upper boom and compression bars are made of concrete,while the lower boom and tension bars are constructed from steel.The vertical deflection of the rooftop’s apex nodeCcan be computed using Eq.(54):

whereSCandSXare the cross-sectional area of the concrete bars and steel bars,respectively.ECandEXare the elastic moduli of the concrete bars and steel bars,respectively.

There are three limit-state functions generated by different conditions of the structure:

The first failure mode occurs when the perpendicular deflectionΔCexceeds 1.5 cm.The second failure mode occurs when the internal force of barADsurpasses its own limiting stress.The third failure mode occurs when the internal force of barECexceeds its respective limit stress.fSdenotes the tensile strength of the bar.Specific setting parameters can be found in reference[154].

Table 6 outlines the system failure probability estimated by SOSA and other methodologies.

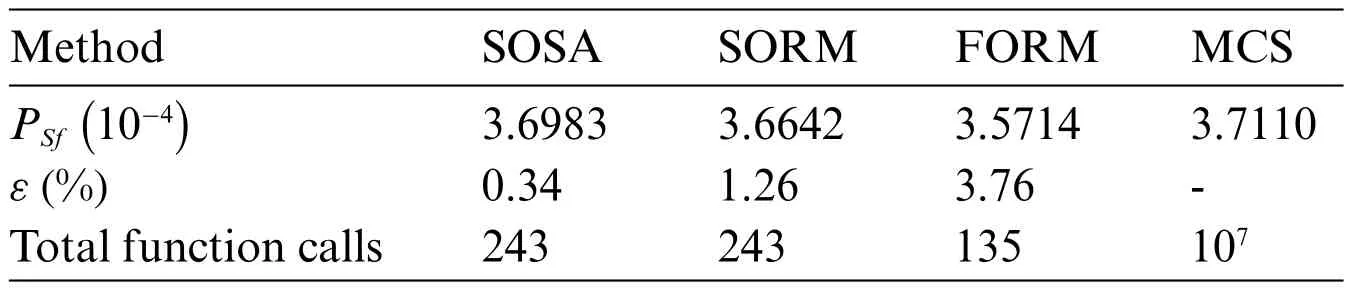
Table 6:Probability of system failure

With the MCS solution as the benchmark,SOSA demonstrates superior accuracy and efficiency,emphasizing the applicability of saddlepoint approximation in engineering contexts.

5 Conclusion

This study comprehensively reviews SAM,explores its enhancement techniques,and provides examples showcasing each augmented SAM in RA.Following these examples,the merits of each method are critically evaluated.The primary goal of SAM is to provide efficient and precise fitting results in RA.Its foundational principles establish a groundwork for effective fitting,adaptable to further refinement based on specific operational needs.RA often involves extensive datasets,posing significant challenges.Remarkably,the results of SAM with minimal sample sizes closely resemble those obtained via MCS with larger sample sizes,indicating SAM’s capability to provide superior approximations even with limited data.Analyzing large-scale samples significantly increases time and financial investments.SAM’s efficiency alleviates substantial operational demands and expedites problem-solving in reliability analysis.However,with the evolving landscape of contemporary engineering,systems requiring RA are growing in size and complexity.An increasing number of uncertainties are being incorporated to ensure the reliability and robustness of extensive mechanical systems.Consequently,achieving a balance between sampling efficiency and reliability is becoming progressively challenging.

In RBDO,challenges arise when the dimensionality of the input information becomes excessively high.Integrating RBDO with saddlepoint approximation removes the need for the spatial transformation of random variables.This approach mitigates potential inaccuracies in reliability assessment caused by amplified nonlinearity in the limit-state function,thereby enhancing the attractiveness of SAM.Presently,the engineering field associated with reliability increasingly tends to adopt machine learning and similar techniques.Utilizing machine learning algorithms enables engineers to construct models derived from data,thereby facilitating predictive analyses and informed decision-making.

The theoretical foundation and validation of SAM remain a dynamic field for future exploration.Its mathematical properties,convergence,and method stability offer significant research value.Additionally,integrating saddlepoint approximation with machine learning models can improve solution accuracy and efficacy.SAM holds potential for utilization in deep neural network (DNN) training.The training processes of DNNs are susceptible to encountering numerous local minima interspersed with saddlepoints,complicating the convergence to a global optimum.SAM can address these saddlepoint challenges during training.SAM involves an effective search in the saddlepoint area to find the saddlepoint and continuous optimization until the global minimum is found.Consequently,SAM can more effectively train DNNs,improving both model accuracy and generalization capability.Integrating saddlepoint approximation into conventional machine learning algorithms,such as support vector machines,logistic regression,and decision trees,enhances model optimization and predictive performance.The amalgamation of SAMs with genetic algorithms is a promising research area.Genetic algorithms,rooted in evolutionary principles,leverage mechanisms such as crossover,mutation,and selection for optimization.Their adeptness at global searching compensates for SAM’s tendency to favor local optimization in high-dimensional spaces.Moreover,genetic algorithms can fine-tune relevant parameters within SAM,enhancing its convergence rate and stability.In essence,combining SAM with these methodologies amplifies its effectiveness in addressing challenges within RA and RBDO.

Acknowledgement:The authors extend their sincere gratitude to the reviewers for their valuable suggestions,which have significantly enhanced the quality of this paper.We also express our heartfelt thanks to the editors for their patience,amiable guidance,and diligent efforts in refining the manuscript.

Funding Statement:This research was funded by the National Natural Science Foundation of China under Grant No.52175130,the Sichuan Science and Technology Program under Grants Nos.2022YFQ0087 and 2022JDJQ0024,the Guangdong Basic and Applied Basic Research Foundation under Grant No.2022A1515240010,and the Students Go Abroad for Scientific Research and Internship Funding Program of University of Electronic Science and Technology of China.

Author Contributions:The authors confirm contribution to the paper as follows: Study conception and design: Debiao Meng,Shiyuan Yang,Yipeng Guo;data collection and analysis: Yihe Xu,Yongqiang Guo;collection and arrangement of references:Lidong Pan,Xinkai Guo;draft manuscript preparation: Debiao Meng,Yipeng Guo.All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials:All data presented in this paper can reasonably be obtained from the relevant references or by contacting the corresponding author of this paper.

Conflicts of Interest:The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article.