玉树地震震前甘孜—玉树断裂局部应力场时空偏转特征的离散元模拟研究

张 涛, 苏占东, 孙进忠, 张建勇, 唐 磊,周 剑, 王 磊, 张明磊

1)防灾科技学院地质工程学院, 河北三河 065201;2)河北省地震灾害防御与风险评价重点实验室, 河北三河 065201;3)中国地质大学(北京)工程技术学院, 北京 100083; 4)中国地震台网中心, 北京 100045;5)北京工业大学城市与工程安全减灾教育部重点实验室, 北京 100124

地壳应力是指由于地壳介质形变而引起的介质内部单位面积上的作用力, 主要由受重力控制的上覆岩层重量产生的自重应力和受地壳构造运动控制的构造作用引起的构造应力两部分组成(李四光,1973)。地壳的应力状态不仅与地壳的构造活动(如地壳形变、断裂、褶皱等构造现象)有关, 而且与人类工程活动密切相关, 譬如, 地下能源开发、核废料长期处置、二氧化碳封存等, 工程场地的应力状态对工程的安全稳定都有关键的控制作用(陈群策等, 2011;Heidbach et al., 2018; 丰成君等, 2022)。因此研究地壳应力状态具有重要的理论意义和实用价值。

断裂活动乃至断裂错动发生地震是区域构造应力作用导致断裂局部地壳应力集中的结果。地壳介质和结构的不均匀性导致地壳应力场的复杂分布,从而局部应力和区域应力之间存在较大差别(苏生瑞等, 2002a; Zhang et al., 2021)。研究表明, 震后震源区总体应力强度会有所下降, 局部最大主应力方向也会发生变化, 震前区域构造应力作用使断裂两盘局部发生错位变形, 导致局部应力场方向与区域应力场方向不一致, 甚至完全相反(陈庆宣等, 1998;孙进忠等, 2015)。

Terzaghi(1923)发现, 不连续面、各向异性和非均质性能导致岩体呈现出复杂的应力状态。Anderson(1937)指出, 断裂的形成会使断裂局部主应力的方向与区域构造应力方向不一致, 应力迹线的转向仅仅发生于断层末端。苏生瑞等(2002a, b)指出, 局部应力和区域应力之间有相当大的差别, 导致这种差别的主要原因之一在于不同尺度断裂构造的发育。目前对地应力的研究方法主要有现场地应力测试、震源机制解和数值模拟等。地应力测量是获得地壳浅表层地应力状态数据最直接、最可靠的方法之一(秦向辉等, 2014; 张鹏等, 2015)。Liao et al.(2003)在2001年昆仑山8.1级地震前后在相同测点开展压磁应力解除试验, 结果表明, 两个测点的应力作用方向分别发生了顺时针和逆时针偏转, 偏转角度分别为21°和63°。原位地应力测量可以提供地壳浅部的实际应力状态, 但是其测量深度浅, 测点少, 很难反映发震断裂错动对深部地壳介质应力状态的影响(王椿镛等, 2003)。计算机技术的快速发展促进了数值模拟方法的实用化, 数值模拟方法具有定量化、可视化等优点, 已广泛应用于地球动力学的各个领域。张淑亮等(2017)对汶川地震前后太原盆地应力场变化特征进行了研究, 研究发现该区域多以走滑断裂为主, 应力场由震前的NNE-SSW向拉张应力为主转为震后NEE-SWW向挤压应力为主且接近华北地区应力场。为了探究应力场偏转的机理, 苏生瑞等(2002b, 2003)采用离散元法模拟研究了断裂及断裂两侧岩石的物理力学性质对断裂局部应力场的影响, 揭示了断裂构造对地应力场的影响规律。Su et al.(2021)运用PFC2D4.0软件模拟甘孜—玉树断裂的破裂过程, 模拟结果表明, 在断裂附近形成了压应力区和拉应力区, 不同位置的局部应力场方向偏转规律存在差异。仲启蒙等(2022)采用有限元数值模拟方法研究地质构造对岩石圈应力场分布的影响, 发现板块运动、岩石圈结构控制整体的构造应力场, 在受水平构造应力控制的区域内,应力场主应力的大小和方向均会受到断裂带不同程度的影响。以上研究结果表明, 断裂活动会导致局部应力场的方向发生变化。

目前大多数研究关注同震和震后应力场的变化, 对震前断裂局部应力场方向的变化规律认识不足, 而震前应力场的偏转变化过程对于断裂活动性的表征和地震预测具有更重要的意义。因此, 本文以甘孜—玉树断裂为研究对象, 建立含有光滑节理的平行粘结本构模型, 根据2010年玉树地震前后玉树地震台站YRY-4型钻孔应变仪的监测数据, 采用PFC2D5.0软件对甘孜—玉树断裂局部应力场进行数值模拟, 研究震前走滑断裂局部应力场的时空偏转特征, 为断裂局部应力场的认识和断裂活动性研究提供依据。

1 研究区构造背景

如图1所示, 甘孜—玉树断裂东南起自四川甘孜, 朝北西方向延伸经过青海玉树, 总长超过400 km, 属于广义的鲜水河断裂带向北西向延伸的一支羽列式断裂带, 为巴颜喀拉地块南边界和青藏高原川滇菱形块体向东南挤出的北部边界(彭华等,2006; 刘莎等, 2012)。1991—1992年, 南水北调西线工程野外考察队对该断裂的重点地段展开了系统的研究工作, 并对断裂带进行了初步的分段。自NW向SE甘孜—玉树断裂可划分为五段: 当江段、玉树段、邓柯段、马尼干戈段和甘孜段, 其中, 甘孜—玉树段长约270 km, 总体呈北西—北西西走向(周荣军等, 1996, 1997)。

图1 玉树地区地质构造图(数据集由中国科学院计算机网络信息中心地理空间数据云提供)Fig.1 Geological structure map of Yushu area(dataset was provided by Geospatial Data Cloud of Computer Network Information Center of Chinese Academy of Sciences)

闻学泽等(1985, 2003)根据对该断裂带新构造特征的初步野外考察指出, 该断裂是一条晚第四纪强烈活动的左旋走滑断裂, 与强震和大地震的发生有密切关系。沿甘孜—玉树断裂带, 除分布有大型燕山期花岗岩外, 还夹杂有三叠系的大量中、基性火山岩, 尤其在断裂带中段分布最广, 反映了在大规模岩浆活动结束的三叠纪后期, 断裂带又有一次强烈的活动。闻学泽等(2003)依据断裂的地貌及相关沉积物特征, 确定出近5万年来断裂带的平均左旋走滑速率为(12±2) mm/a, 垂直滑动速率为0.6～1.2 mm/a。2010年4月14日在此断裂带上发生了MS7.1级玉树地震, 震中位于33.2°N、96.6°E, 震源深度约为14 km, 玉树地震发生后约1.5 h, 在主震震中位置附近又发生一次MS6.3级余震, 震中位置为33.23°N、96.58°E, 震源深度约10 km, 此后,又有38次MS＞3的余震发生, 其中包括7次MS＞4.8的余震(张勇等, 2010; Ekström et al., 2012)。石学录等(2017)通过CPA方法反演分析玉树7.1级地震序列前震、主震、余震的震源机制解, 发现19个结果中以走滑类型为主, 前震、主震的震源机制解非常接近, 反映出前震和主震之间密切联系, 甘孜—玉树断裂北支玉树—隆宝断裂为此次地震的发震构造,震源机制解类型较为简单, 为巴颜喀拉地块与羌塘块体边界处甘孜—玉树断裂能量的正常释放。以上的断裂滑动变形和地震活动数据表明, 甘孜—玉树断裂带是一个活跃的发震断层。

2 YRY-4钻孔应变仪及数据分析

钻孔应变仪是一种研究地壳浅表地应力状态的全频段观测仪器, 在地震地球物理观测中占有重要地位(李海亮等, 2010; 娄家墅等, 2022)。YRY-4型四元件钻孔应变仪具有观测精度高、连续性和稳定性好等优点, 广泛应用于地应力的测量(侯林锋,2015)。如图2a所示, 目前在中国大约有40个YRY-4型四元件钻孔应变仪站点, 采样频率为每分钟1个数据点或每小时1个数据点(Qiu et al., 2013)。本次测量数据来源于安装在玉树台站的YRY-4型四元件钻孔应变仪。玉树台站(E: 97.02°, N: 33.01°, H:3 725 m)位于青海省玉树藏族自治州政府所在地结古镇, 该台址基岩为花岗岩(图1)。仪器探头置于深度为39.5 m钻孔中与孔壁耦合, 探头中有四个水平放置的元件, 相邻元件之间的夹角皆为45°, 可用来测量四个方向的孔径相对应变。用εi(i=1, 2, 3, 4)表示安装在钻孔中的四个元件及其测量值, 因主应变及其主方向与坐标系的选择无关(刘序俨等, 2014), 本文中选择元件ε2的方向作为Y轴, 与ε2成正交方向的元件ε4为X轴, 探头端面中心作为坐标原点O(图2b)。

图2 四元件钻孔应变仪的分布与YRY-4型钻孔应变仪测量元件图Fig.2 Distribution of four-element borehole strain gauges and diagram of measuring elements of the YRY-4 boreholestrain gauge

玉树台站四元件钻孔应变仪经安装耦合校准后, 自2008年1月3日开始正常运行至今, 因此可截取2010年4月14日玉树地震发生前后的原始数据进行分析。根据公式(1)计算测点最大主应变方向φ, 假定最大主应变方向与区域构造应力方向一致,则主应变方向的变化即为偏转角Δθ(Su et al.,2021)。本研究区采用的应力方向主要基于研究区附近的GPS速度场, 研究区内7个台站测得的GPS速度平均方向与水平轴(E-W)呈逆时针方向约10°夹角, 表明原位SH方向接近N80°E(Zheng et al.,2017)。

式中:θ1为测点最大主应变方向与Y轴间夹角, 绕Y轴逆时针为正;θ2为测量元件ε2的方位角, 即Y轴与正北方向N的夹角;φ为测点最大主应变的方位角(此处假设等同于测点的最大主应力方位角), Δθ为偏转角。

通过数据分析发现, 2010年4月13日玉树地震发生前, 应变随时间变化总体呈现下降趋势, 当地震发生后,ε3、ε4开始上升,ε1、ε2出现下降(图3a)。这可能与该区域最大主应力方向在ε3、ε4夹角之间,最小主应力方向在ε1、ε2之间有关。根据玉树台站实际监测数据计算得出, 在震前断裂局部最大主应力方向和区域最大主应力方向间的夹角偏转了28°左右, 玉树台站附近最大主应力方向先顺时针旋转,再逆时针旋转后基本保持恒定。玉树地震发生后,测点最大主应变方向与区域构造应力场最大主应力方向(N80°E)之间的夹角迅速减小, 偏转角发生逆时针旋转, 一段时间后, 偏转角逆时针旋转的变化率逐渐降低, 并逐步恢复至起始监测水平(图3b)。以上结果说明, 地震发生前, 断裂带附近局部主应力方向会发生明显偏转, 与区域构造应力场方向之间的夹角逐渐增大, 当地震发生后, 应力得到释放,局部应力场主应力方向逐步恢复到原来的状态。

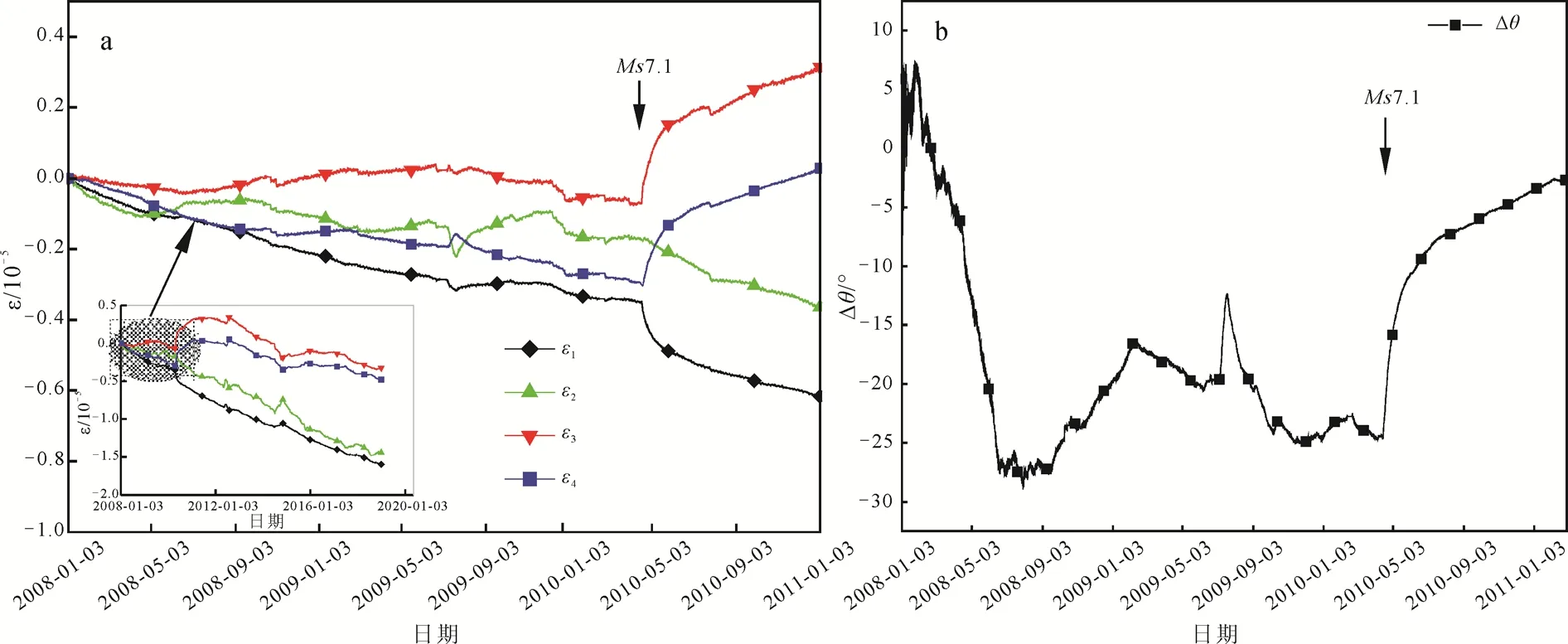
图3 玉树台站YRY-4型钻孔应变仪观测应变及最大主应变偏转角随时间的变化曲线Fig.3 Variation curve of observed strain and maximum principal strain deflection angle with time of the YRY-4 borehole strain gauge at the Yushu station

3 数值模拟

3.1 模型建立与参数确定

考虑图1所示甘孜—玉树断裂带的地理分布特征, 构建如图4所示的甘孜—玉树断裂二维几何模型, 利用PFC2D软件生成相应的数值模型, 模拟区域构造应力作用导致的甘孜—玉树断裂局部应力场的变化。模型长240 km, 宽200 km。刘超等(2010)根据波形资料反演获得玉树地震的发震断层走向为119°, 倾角为83°。在模型中, 按甘孜—玉树断裂实际出露的形迹确定断裂段在模型中的平面形态, 并将断裂简化为一定深度范围内产状直立的走向滑动断裂, 采用光滑节理模型(Smooth-joint Contact Model, SJM)模拟断裂段的力学效应, 将断裂段周边一定深度范围内的地质体简化为颗粒聚合体, 模拟断裂周边局部介质的变形及应力场变化。

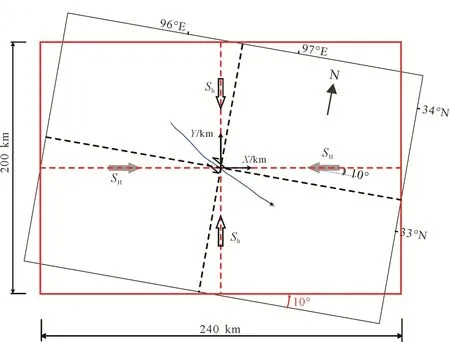
图4 甘孜—玉树断裂二维数值模型(几何模型)Fig.4 Two-dimensional numerical model of Ganzi-Yushu fault (geometric model)

为有效模拟区域构造应力作用导致的甘孜—玉树断裂段周边局部应力场变化, 需根据甘孜—玉树断裂的实际地质条件提炼确定甘孜—玉树断裂的二维数值模型参数。按照所建立的数值模型, 模型参数包括三个部分: 模型介质颗粒单元的几何和物理力学参数; 模型介质颗粒间接触的力学模型参数;断裂单元的几何形态参数和断裂两盘接触的力学模型参数。

3.1.1 模型介质颗粒单元参数

颗粒单元参数包括几何参数和物理力学参数两部分。二维模型介质颗粒单元设为圆形, 颗粒尺度大小的确定原则上要考虑模拟的精度和效率两个方面。从模拟精度考虑, 颗粒尺度越小越能细致地模拟介质的细微变化, 但是颗粒尺度过小会导致计算量过大; 从模拟效果看, 颗粒尺度会对颗粒分布和细观粘结强度产生影响, 颗粒尺度较大会使模型介质呈现出非均匀性和各向异性特征, 但是颗粒尺度过小有可能会有颗粒单元穿过模型边界, 进而影响模拟效果。模拟实践中采用模型尺度L与颗粒半径R的比值控制颗粒尺度的大小。研究表明, 当模型尺度L与颗粒半径R之比小于下限(L/R)min=125时, 模拟效果会受到显著影响(赵国彦等, 2012; 杨家琦, 2018)。根据上述原则, 考虑所建模型尺度和断裂局部应力场模拟效果的要求, 颗粒单元的半径R设定在350～550 m之间, 模型尺度与颗粒半径的比值(L/R)大约在363～686之间, 远大于有效模拟对应的模型尺度与颗粒半径比的下限值(L/R)min, 因此,本文所设定的颗粒尺度对模拟效果的影响可以忽略不计。

组成模型介质的颗粒设为均匀各向同性弹性介质, 主要考虑颗粒单元的弹性变形和极端情况时的受压破坏, 因此, 颗粒介质的物理力学参数主要包括颗粒介质密度、弹性模量、泊松比等。甘孜—玉树断裂数值模型参数的具体赋值情况见表1。

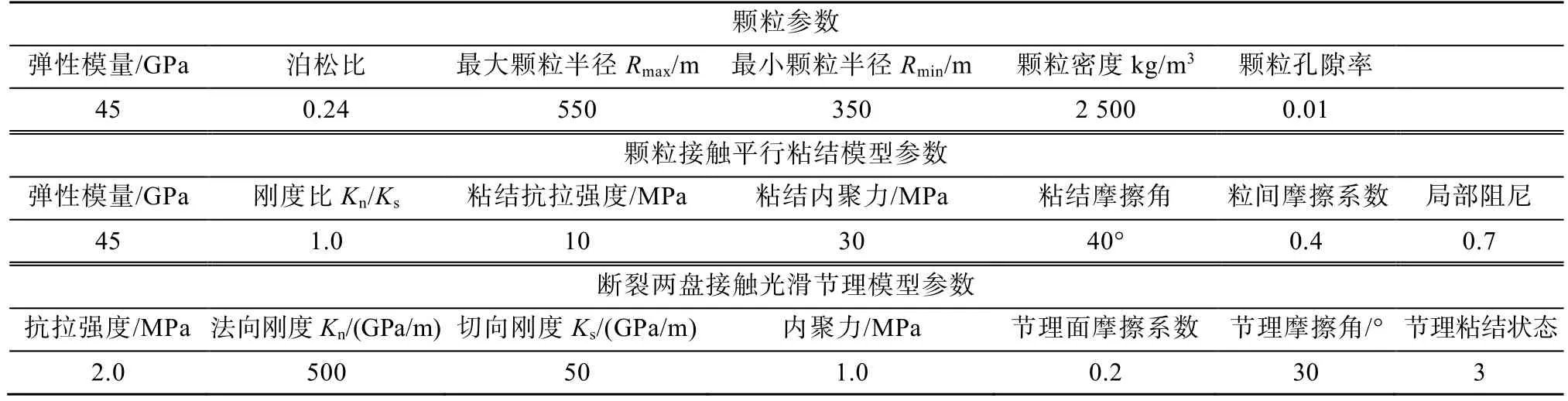
表1 甘孜—玉树断裂数值模型参数Table 1 Parameters of the numerical model of the Ganzi-Yushu fault

3.1.2 颗粒单元之间接触的力学模型及其参数

在PFC数值模型中, 颗粒单元之间接触本构关系采用平行粘结模型(Bonded-Particle Model,BPM), BPM是指相互接触的颗粒在有限范围内产生力学行为, 且颗粒之间既能承受拉压力和摩擦力,又可以承受力矩(Potyondy et al., 2004; 石崇等,2018)。颗粒单元之间接触的平行粘结模型包括法向及切向弹簧、摩擦阻尼器和摩擦滑块。据此, 描述颗粒单元粘结模型力学性质的参数主要有颗粒间接触的法向刚度(Kn)和切向刚度(Ks)、法向阻尼(法向粘滞系数ηn)和切向阻尼(切向粘滞系数ηs)。颗粒接触力学本构模型的参数也包括颗粒单元接触变形涉及到的颗粒单元自身材料的弹性模量(E)和泊松比(ν)。颗粒单元粒间接触的平行粘结模型参数的赋值见表1。

3.1.3 断裂几何参数和断裂两盘接触的力学模型参数

为研究甘孜—玉树断裂段在构造应力作用下走滑错动派生的断裂局部应力场, 二维模型考虑2 km深处的断裂走滑运动。为使数值模型中所构建的断裂模型尽可能真实地反映甘孜—玉树断裂段的几何形态, 将甘孜—玉树断裂形迹线沿走向自NW向SE依次划分为13个近于平直的线段, 断裂各分段的几何参数列于表2中。

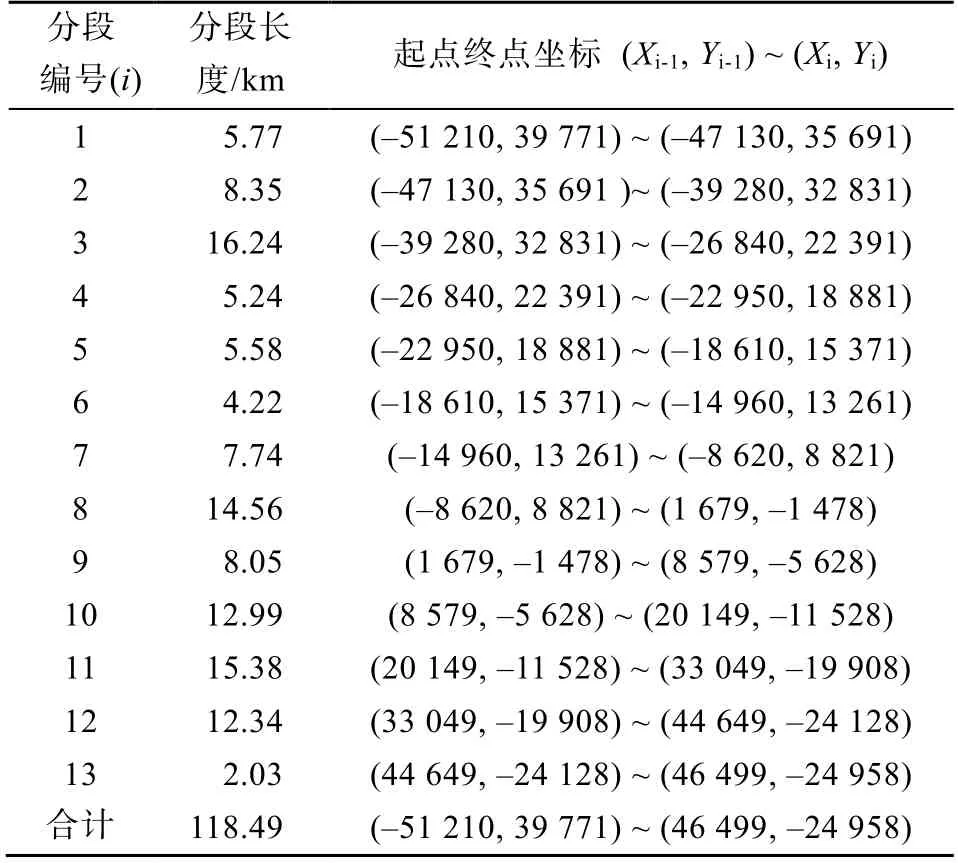
表2 甘孜—玉树走滑断裂带分段几何参数Table 2 Sectional geometric parameters of Ganzi-Yushu strike-slip fault zone

所建立的甘孜—玉树断裂数值模型中断裂两盘接触的力学模型采用光滑节理模型(SJM)。SJM假定断裂面光滑, 断裂面的抗剪切强度由断裂两盘在一定法向压力作用下的接触摩擦形成, 可分为静摩擦强度τ0和动摩擦强度τs, 分别对应静摩擦系数µ0和动摩擦系数µs。构造作用在断裂面上产生的剪应力小于断裂面发生错动的强度时, 断裂两盘运动会牵动断面附近两盘介质发生弹性变形, 断裂面所受剪力与断裂两盘变形位移之间的比例系数即为切向刚度Ks, 类似地,所受法向力与断裂两盘法向变形位移之间的比例系数为法向刚度Kn。甘孜—玉树断裂数值模型中断裂的光滑节理模型参数具体赋值也列于表1中。

颗粒单元、颗粒接触模型参数以及断裂模型参数确定后, 即可构建生成数值模型。如图5所示,首先随机生成一个半径在350～550 m之间的小尺寸区域块, 然后由其组装成赋有66 420个颗粒的不含节理面的完整模型试样, 并根据花岗岩物理力学性质的经验值对颗粒赋予细观参数, 最后以“geometry”形式将SJM置于组装后赋予BPM接触的完整模型中构建裂隙, “geometry”两侧颗粒的BPM接触被SJM接触取代, 相邻颗粒能够沿着节理面发生平滑的相对滑动而不受颗粒接触方位的影响, 通过不断伺服加载调整模型细观参数, 使数值模拟宏观参数符合经验值, 从而实现模型的细观参数标定(表1), 最终生成模拟研究采用的离散元数值模型。

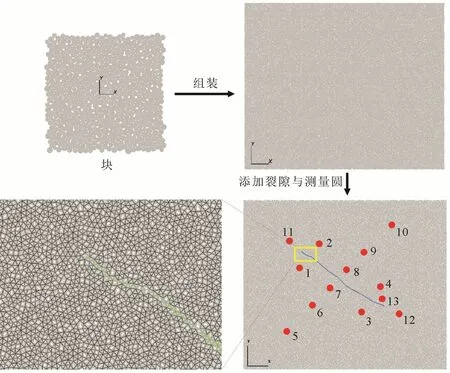
图5 甘孜—玉树断裂数值模型颗粒元介质及断裂建模示意图Fig.5 Schematic diagram of particle element medium and fracture modeling of numerical model of Ganzi-Yushu fault

3.2 模拟工况及测量圆布置

3.2.1 模拟工况

将甘孜—玉树断裂所处的区域构造应力场转化为甘孜—玉树断裂数值模型边界荷载, 展开区域构造应力作用导致的断裂局部应力场数值模拟, 揭示断裂两盘地质体中局部应力的发展过程和空间分布。通过比较断裂局部应力场相对于区域构造应力场的变化, 筛选能够表征断裂活动程度的关键参数,譬如, 局部应力场最大主应力方向相对于区域构造应力场最大主应力方向的偏转。考察关键参数随构造应力作用的变化过程及其与断裂活动程度变化的对应关系, 确定关键参数对应断裂发震临界状态对应的参数阈值, 对断裂发震危险性评价具有重要意义。

甘孜—玉树断裂二维离散元数值模型生成后,需确定数值模型的加载方案, 才能展开甘孜—玉树断裂局部应力场变化的数值模拟。首先考察甘孜—玉树断裂所处的区域构造应力场情况。研究表明,地应力场中的中间主应力σ2方向近似为垂向, 而最大主应力σ1和最小主应力σ3基本在水平面内, 分别记为SH和Sh。如式(2)所示, 区域构造应力场两个正交的水平主应力分量的量值随深度Z(m)的增加而增大, 但在不同的深度上用应力解除法和水压致裂法等进行应力测量的最大主应力的方向随深度的变化不大(Haimson, 1978; 李方全等, 1982; 廖椿庭等,1983)。

式中: 应力分量SH、Sh的单位为MPa。

可见, 浅部的地应力测量结果能够反应区域构造应力场的方向特征。根据公式(2), 杨树新(2013)通过对中国陆域地壳应力场分布特征的研究发现,青藏高原2 km处水平最大主应力SH约为64 MPa,水平最小主应力Sh约为38 MPa, 水平最大主应力方向为N80°E。

根据上述甘孜—玉树断裂带区域构造应力场的研究成果, 取断裂带区域构造应力场的最大水平主应力SH(大小64 MPa, 方向N80°E)和最小主应力Sh(大小38 MPa, 方向N10°W)作为对甘孜—玉树断裂数值模型的施加荷载(图4)。由于建模区域边框相对于经纬坐标系的旋转存在10°偏差, 在模型中X轴与加载最大主应力SH平行(N80°E), 与加载最小主应力Sh垂直, 与X轴平行的模型边界为最小主应力Sh加载边界;Y轴与加载最小主应力Sh方向平行(N10°W), 与加载最大主应力SH方向垂直, 与Y轴平行的模型边界为最大主应力SH加载边界, 以便在模型中产生的剪切力与实际工况相符。

3.2.2 测量圆布置

如图5所示, 为研究断裂沿线局部主应力的空间变化规律, 在模型断裂两个端部与断裂对称各设置了2个测量圆(NW端测点1、2, SE端测点3、4),在断裂两端延长线上各设置了1个测量圆(NW端测点11, SE端测点12), 在断层中部垂直于断裂走向对称设置了6个测量圆(SW盘测点5～7, NE盘测点8～10), 此外, 在对应实际玉树台站钻孔应变仪安装井位置上布置了1个测量圆(测点13)。上述模型监测点的位置坐标列于表3中。

表3 测量圆位置几何参数Table 3 Geometric parameters of measuring circle position

利用数值模型上布置的这些测量圆, 可以获得模型加载过程中测点处模型介质的应力(σx,σy,τxy)。

4 玉树地震震前断裂局部应力场的演化规律

在数值模型上布置的监测点可以获得数值模型加载过程中监测点(测量圆)处每一时步的应力分量σx、σy、τxy, 将这些应力分量带入公式(3), 即可求出监测点处断裂局部应力场最大主应力方向相对于加载最大主应力方向的偏转角度。

式中:θ为局部应力场最大主应力方向与模型观测坐标系中X轴的夹角, 由于X轴方向就是最大加载应力SH的作用方向, 因此, 这个角度就是局部应力场最大主应力方向与最大加载应力作用方向之间的偏转角, 即θ=Δθ。

模拟结果显示, 断裂破坏前测量圆13的Δθ随时步逐渐减小, 局部主应力发生逆时针旋转, Δθ从加载初期到断裂破坏前的变化幅度达15°左右, 预示断裂带积累了一定的应变能。在160 000步左右Δθ突然开始增大, 局部最大主应力方向旋转得到恢复, 这可能是由于断裂附近颗粒受到的应力大于平行黏结模型强度时, 颗粒间的平行黏结接触发生破坏所致(图6)。这与阿拉善左旗5.8级地震震前巴彦浩特盆地的最大主应力方向发生大幅度偏转, 震后最大主应力方向与区域构造应力场方向趋于一致的结论相吻合(李娟等, 2020)。同时, 数值模拟结果与玉树台站四元件钻孔应变仪现场实测的局部主应力方向的变化趋势基本一致, 说明此模型可用于断裂局部应力场方向变化的模拟。

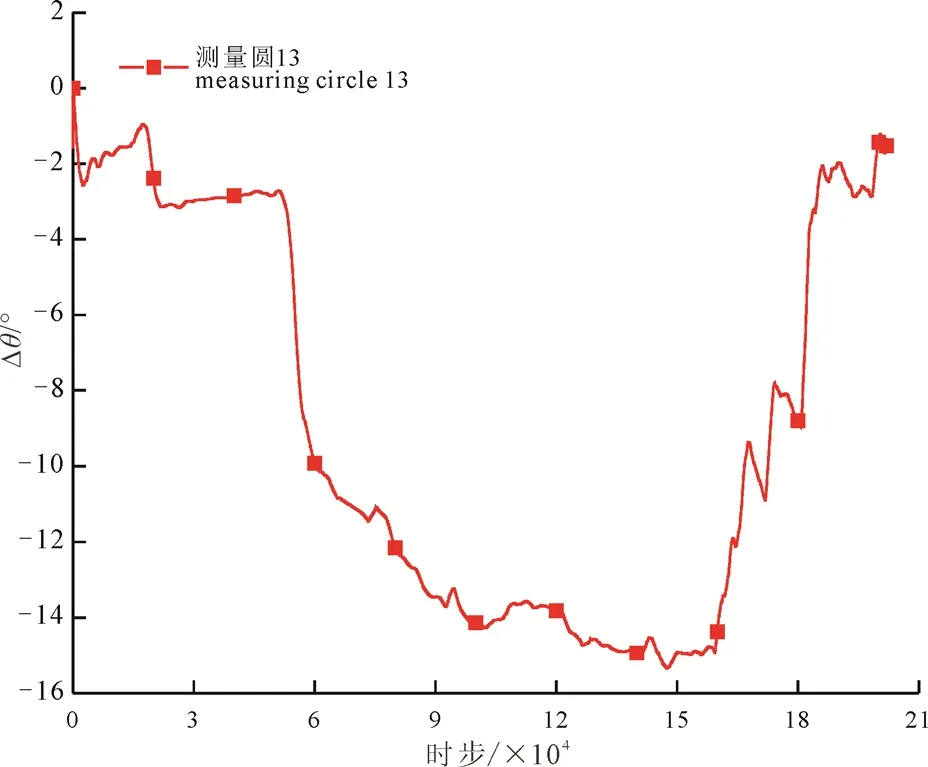
图6 模拟玉树台站位置测量圆偏转角随时步的变化曲线Fig.6 Change curve of simulated Yushu station position measurement circle for deflection angle at any time step

如图7所示, 在加载的初始阶段, 模型中颗粒左下角先受到挤压, 颗粒逐渐向模型中部位移(图7a), 随着水平向荷载的不断增大, 颗粒位移方向在断裂接触面处发生偏转(图7b), 随着断裂接触面的荷载逐渐增大, 断裂两端伴随着裂纹的出现, 断裂面两侧的颗粒位移方向朝着相反方向位移的角度增大(图7c), 在加载基本结束时, 断裂两端出现大量裂纹, 两侧颗粒位移发生反向相对运动(图7d)。

图7 不同阶段颗粒的位移云图Fig.7 Particle displacement nephogram at different stages

如图8所示, 模型主要是以张破坏为主。加载初期主要是在预制构造断裂处出现了剪裂纹(图8a);随着荷载的增加, 预制断裂两侧和模型边界开始出现张裂纹(图8b); 当断裂两端的裂纹扩展到一定程度后, 裂纹不仅继续沿着节理走向扩展, 而且在最小主应力方向出现裂纹并继续扩展(图8c); 随着加载的进行, 裂纹不仅在数量上进一步增加, 且沿着最小主应力方向进一步扩展, 直至构造断裂两端裂纹形成贯通(图8d)。

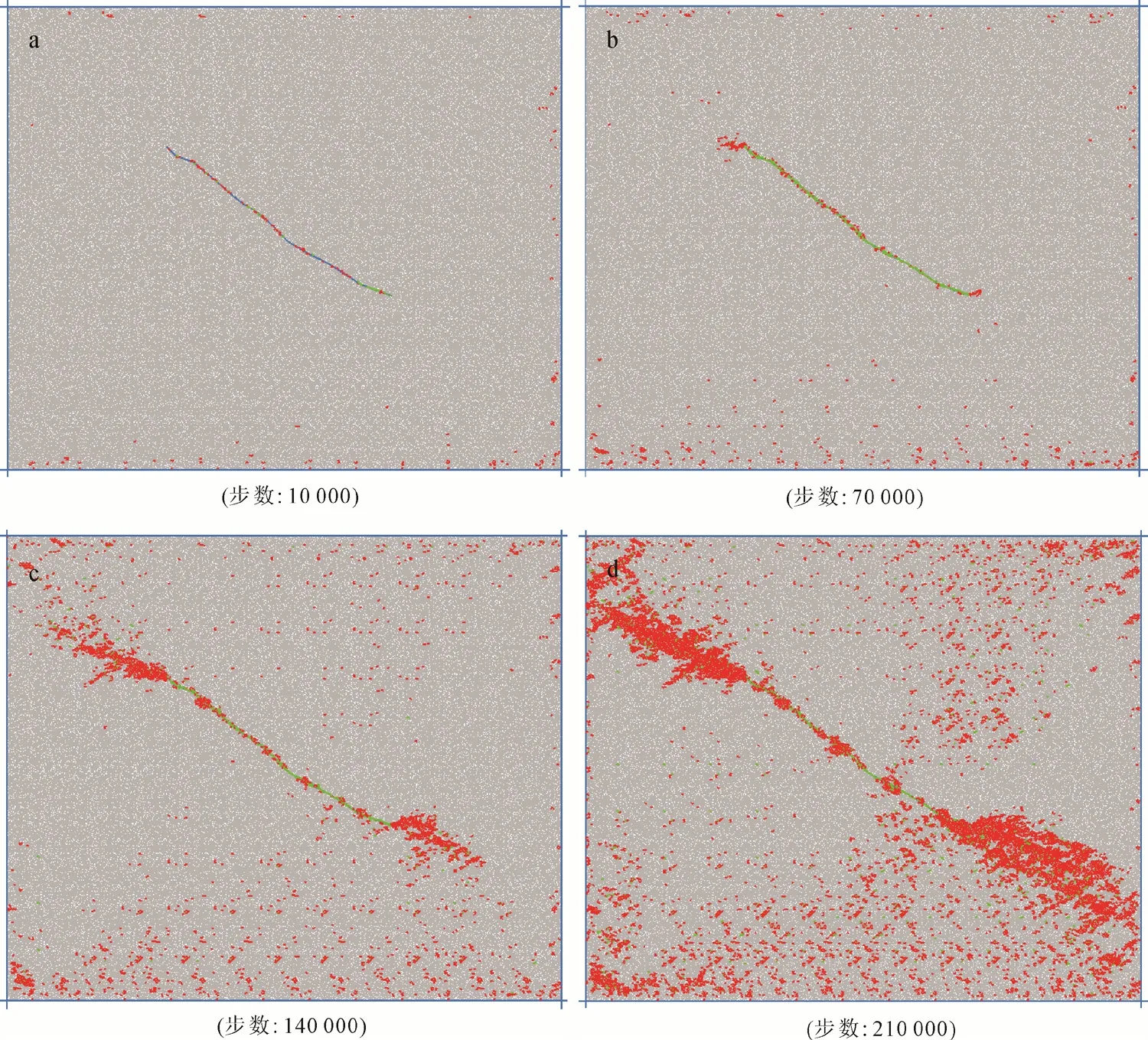
图8 数值模型破坏裂纹图Fig.8 Crack diagram of numerical model failure

为研究加载过程中指定区域应力方向的时空变化规律, 选择了四个时间节点, 即初始加载阶段、裂纹萌生阶段、裂纹发育阶段以及裂纹贯通阶段。在加载初始阶段, 应力由模型四周向中心传递并在断裂接触面处形成应力集中区(图9a); 在裂纹萌生阶段, 随着拉裂纹数量的增多, 断裂接触面的应力集中度逐渐提高(图9b); 随着加载的不断进行, 在模型中部应力集中度加强的同时, 断裂两侧形成了不同的压应力区和拉应力区(图9c); 当裂纹数量大量增多并产生贯通时, 除断裂周围外, 整个模型区域平均最大主应力随空间分布相对均匀, 拉应力集中区的范围逐渐扩大, 压应力集中区的范围逐渐减小,拉伸应力和压缩应力区域的集中度不断提高, 且模型中部出现了应力降现象(图9d)。这与张勇等(2010)对玉树地震断层面和板内地震的应力降反演结果基本一致。从应力云图可以看出, 最大主应力集中区位于模型中部, 这与玉树地震震中所在位置高度契合。以上结果说明, 在整个模型加载过程中, 区域构造应力场的最大主应力随空间分布相对均匀, 随时间平稳变化, 而断裂局部应力场的变化较复杂。

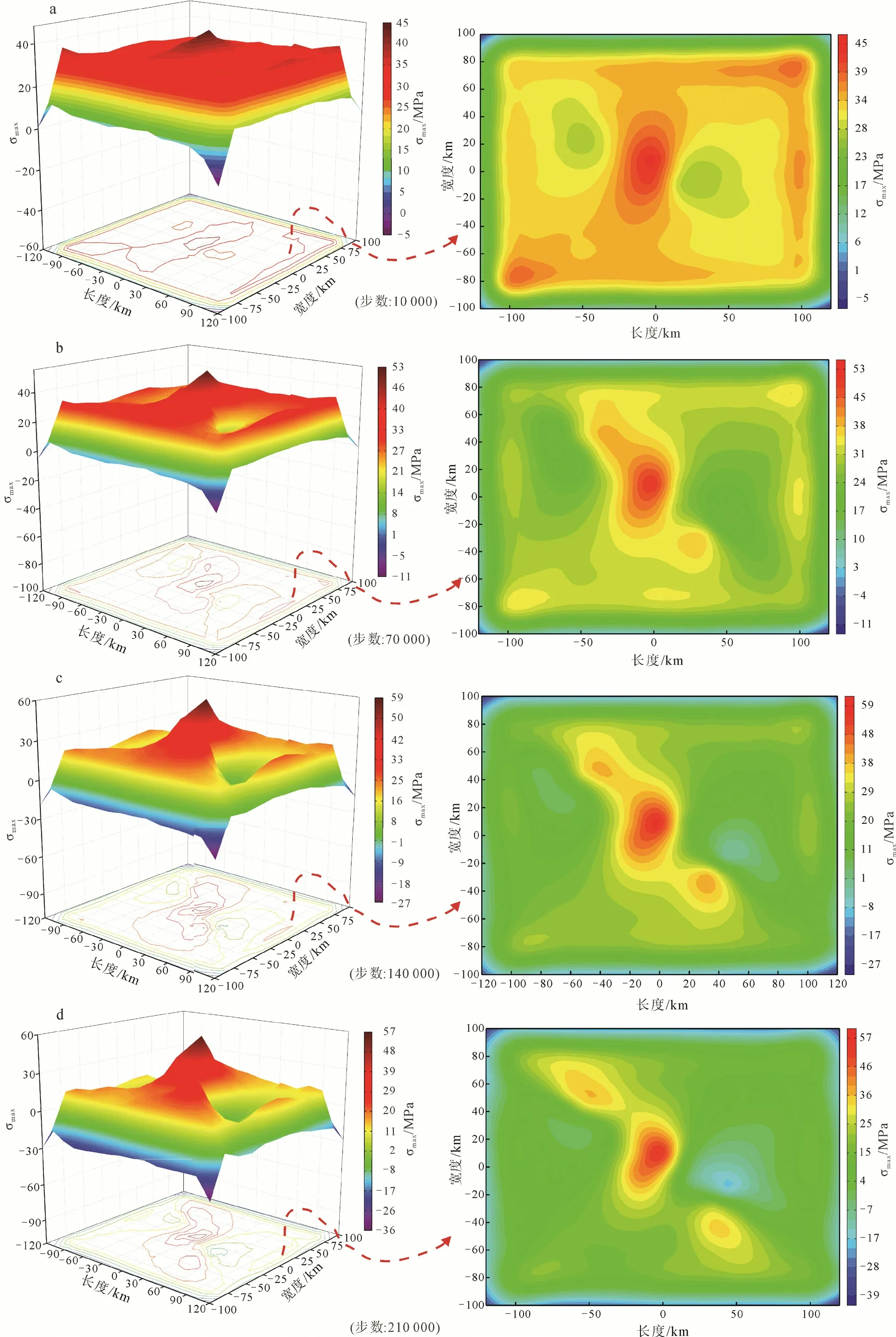
图9 颗粒应力云图Fig.9 Particle stress nephogram

如图10所示, 位于拉应力区的测量圆1、4的偏转角随加载时步的变化趋势基本一致, 在47 000步左右Δθ逐渐减小, 局部最大主应力SH逆时针偏转, 由于破裂的发生, 测量圆1和测量圆4的Δθ分别从110 000步和160 000步左右逐步增大, 向反方向旋转; 位于压应力区的测量圆2、3的偏转角随时步的变化趋势基本一致, 在47 000步左右开始Δθ逐步增大, 局部最大主应力SH顺时针旋转, 在160 000步左右处产生破裂, 偏转幅度明显增大(图10a)。位于断裂两端的测量圆11、12的Δθ随加载时间的增加逐步增大, 在160 000步左右处开始突然向反方向旋转, 预示破裂在此刻产生(图10b)。由此说明, 模型并非属于理想弹性体, 不同区域的应变能积累程度不同, 且随着加载时间的推移而扩大,破裂并非在同一时刻发生, 具有明显的时空效应。

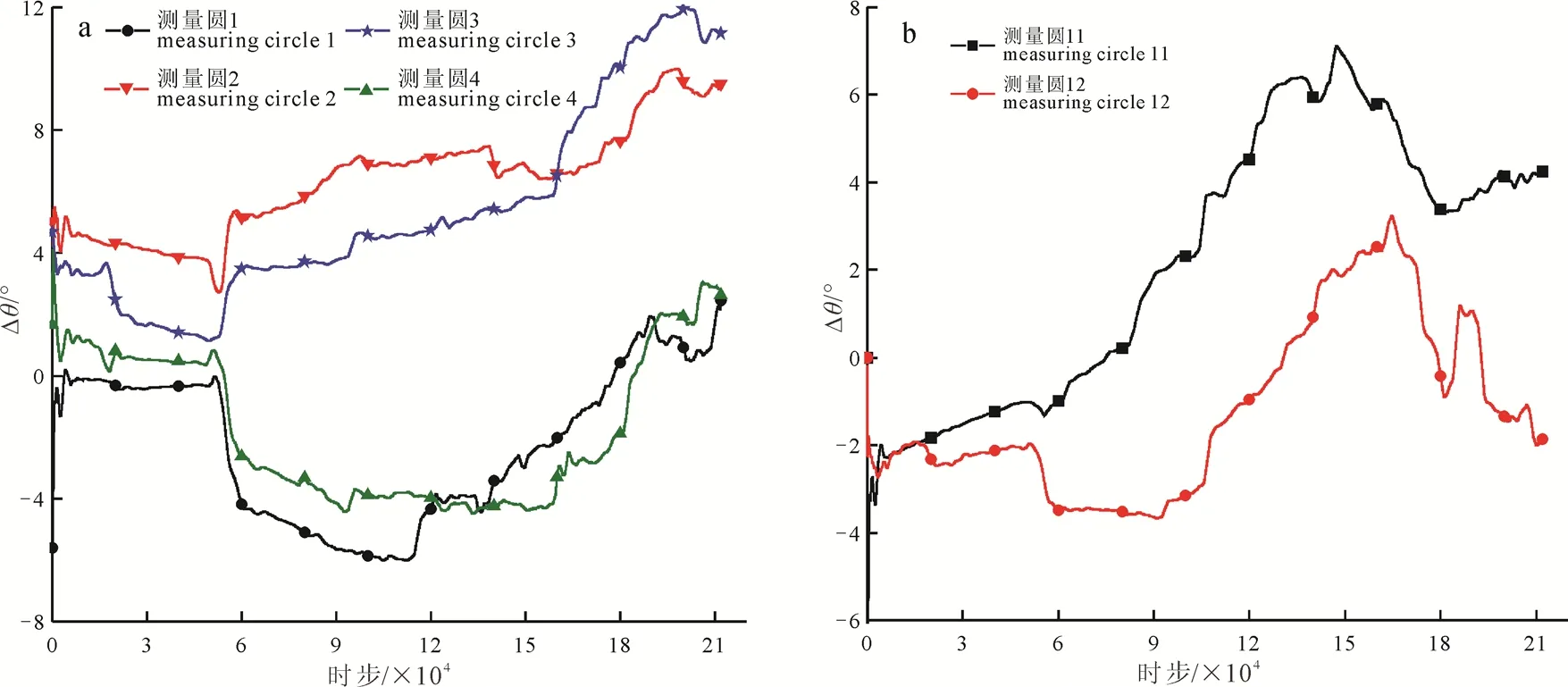
图10 不同区域测量圆的偏转角随时步的变化曲线Fig.10 Variation curve of deflection angle of circle measured in different areas at any time step

如图11所示, 垂直于断裂剖面线两侧6个测量圆的变化趋势与拉压应力区相比较缓和。与断裂相距最远的测量圆5和10的局部主应力方向基本保持不变, 靠近断裂处的测量圆7和8的局部主应力方向偏转幅度最大, 达22°左右, 处于中间位置的测量圆6、9的局部主应力方向变化在两者之间(图11a),由此说明, 距离断裂越近, 局部主应力方向受到的扰动越明显, 而远离断裂的位置, 局部主应力方向受区域应力场控制, 其应力方向趋于应力加载方向。同侧靠近断裂测量圆的Δθmax比远离断裂测量圆的Δθmax大, 且断裂左侧的测量圆5、6相较于断裂右侧的测量圆9、10的Δθmax大, 说明断裂左侧区域应力场受到的扰动比右侧区域大(图11b)。这与Su et al.(2021)等对于Δθmax随着距离断裂处位置增加而减小的结论一致。

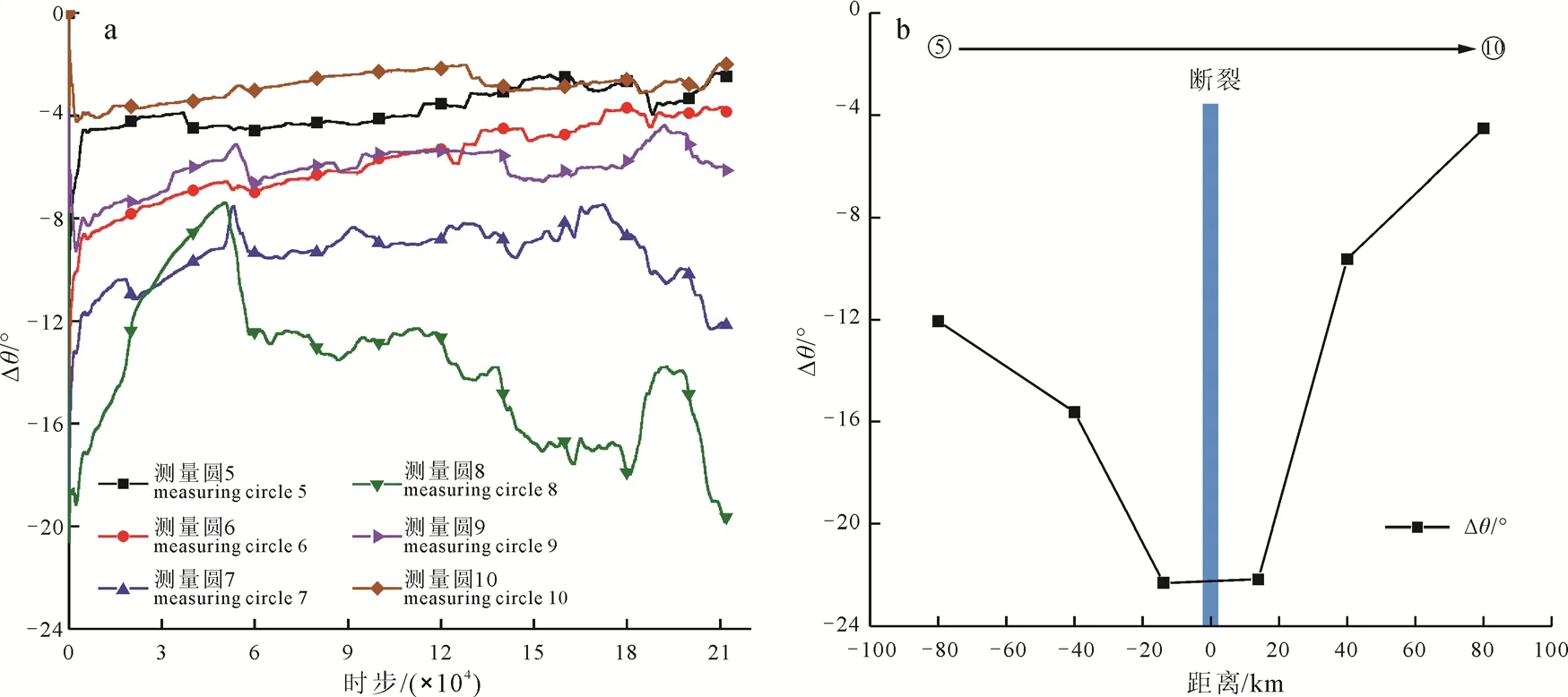
图11 垂直剖面线两侧偏转角的变化规律Fig.11 Variation of deflection angle on both sides of the vertical profile line

5 结论

本文基于平行黏结接触和光滑节理接触模型,建立了一种模拟走滑断裂局部应力场的颗粒流模型,用来分析甘孜—玉树断裂震前局部应力场方向的时空偏转特征, 得到如下主要结论:

(1)模拟玉树台站位置的局部主应力方向变化趋势与玉树台站YRY-4型四元件钻孔应变仪实测的局部主应力方向变化趋势基本一致, 表明在应力作用下构造断裂局部主应力方向会产生偏转, 直到构造断裂发生破裂后局部主应力方向开始逐步恢复并趋向于应力加载方向。

(2)在荷载作用下, 预制构造断裂处先产生剪裂纹, 后出现张裂纹, 随着裂纹数量进一步增加, 最终在构造断裂两端形成贯通, 模型整体以张破坏为主。断裂局部形成拉压应力区, 拉应力集中区的范围逐渐扩大, 压应力集中区的范围逐渐减小, 且拉压应力区的集中度不断提高。

(3)震前位于拉应力区和压应力区的局部最大主应力向相反方向旋转, 偏转角随时步的增加逐步增大, 不同区域的应力积累程度不同, 且随着加载时间的推移而扩大, 并在不同时刻发生破裂, 具有明显的时空效应。

(4)垂直于断裂剖面线上, Δθmax随着距离断裂位置的增加而减小, 距离构造断裂越近, 受到的扰动越明显, 且断裂两盘受到的扰动程度不同。

该研究只针对甘孜—玉树断裂带中玉树段展开研究, 未考虑断层的产状及复合断层等对断裂力学行为演变的影响, 在不断加载的过程中, 由于构造断裂走向的影响, 导致应力分布存在一些差异,在模型中部存在明显的应力集中区, 这一现象表明构造断裂的产状会对试样内部的应力分布产生显著影响。该模拟断裂破坏前的时间尺度虽与实际物理过程无法对应, 但是能较好地模拟断裂在缓慢错动过程中应力发生的时空偏转特征。在后期的研究中,将基于颗粒流进一步探索构造断裂局部应力场随其产状以及复合断裂的变化情况, 有助于全面把握研究区域应力的分布规律, 为断裂的活动性评价提供更多依据。

Acknowledgements:

This study was supported by the Fundamental Research Funds for the Central Universities (Nos.ZY20220319 and ZY20215113), National Natural Science Foundation of China (No.41807270).