2023年高考物理湖南卷第15题“椭圆摆模型”的研究

段石峰

(长沙市周南中学,湖南 长沙 410201)

湖南省近3年的新高考物理试题稳中有变,总体向好的方向发展,更加有利于拔尖创新人才选拔,符合新时代教育评价改革和教育强国建设的要求．2023年第15题的设计非常创新巧妙,摒弃了“重数学运算技巧,轻物理思维方法”的常规做法,让人眼前一亮、耳目一新．本文在对该试题深入解读的基础上,从试题溯源的“球槽模型”拓展为“椭圆摆模型”,以便在教学中强化模型建构的意识,促进科学思维能力的培养,从而提升学生的核心素养．

1 试题呈现

例题.(2023年高考湖南卷第15题)如图1所示,质量为M的匀质凹槽放在光滑水平地面上,凹槽内有一个半椭圆形的光滑轨道,椭圆的半长轴和半短轴分别为a和b,长轴水平,短轴竖直．质量为m的小球,初始时刻从椭圆轨道长轴的右端点由静止开始下滑．以初始时刻椭圆中心的位置为坐标原点,在竖直平面内建立固定于地面的直角坐标系xOy,椭圆长轴位于x轴上．整个过程凹槽不翻转,重力加速度为g．

图1 小球在凹槽内的运动

(1) 小球第1次运动到轨道最低点时,求凹槽的速度大小以及凹槽相对于初始时刻运动的距离;

(2) 在平面直角坐标系xOy中,求出小球运动的轨迹方程;

2 试题解读

2.1 第(1)问解读

第(1)问是通常涉及的特殊位置,还有“人船模型”的变形迁移．从知识的角度,考查动量和能量的综合应用;从能力的角度,考查理解能力和推理论证能力;从素养的角度,考查科学思维中的模型建构和科学推理要素．这两个小问题都与凹槽内轨道的具体形状无关．

解析:凹槽放在光滑的水平地面上不固定,小球释放后下滑时凹槽向右运动,系统在水平方向不受外力．设小球运动到最低点时相对于地面的速度为v1,凹槽的速度为v2,由系统的水平方向动量守恒可得

mv1=Mv2.

(1)

水平地面和凹槽内轨道均光滑,由系统的机械能守恒可得

(2)

联立式(1)(2)解得

(3)

从式(3)的结果来看,v1和v2与水平方向的长半轴a无关,与竖直方向的短半轴b有关．

由式(1)对时间微元求和可得水平位移关系

mx1=Mx2.

(4)

而且水平方向存在几何关系

x1+x2=a.

(5)

联立式(4)(5)解得

(6)

从式(6)的结果来看,x1和x2与水平方向的长半轴a有关,与竖直方向的短半轴b无关．

2.2 第(2)问解读

第(2)问是第(1)问的进阶,将特殊位置的确定量延伸到任意位置的变量,涉及到轨迹形状的变换,其实就是以静止释放点为定点,水平方向按一定的比例压缩,而竖直方向不变．这个问题与小球和凹槽之间是否光滑无关,与小球是否具有竖直方向的初速度也无关．

解析:设小球在坐标系xOy中的坐标为(x,y),则小球向左运动的水平位移为(a-x)．设凹槽向右运动的位移为x3,由式(4)可得

(7)

凹槽移动后的半椭圆形轨道方程为

(8)

小球始终在凹槽半椭圆形轨道上,式(8)即为小球运动的轨迹方程,联立式(7)(8)解得

(9)

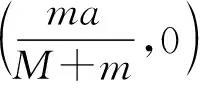
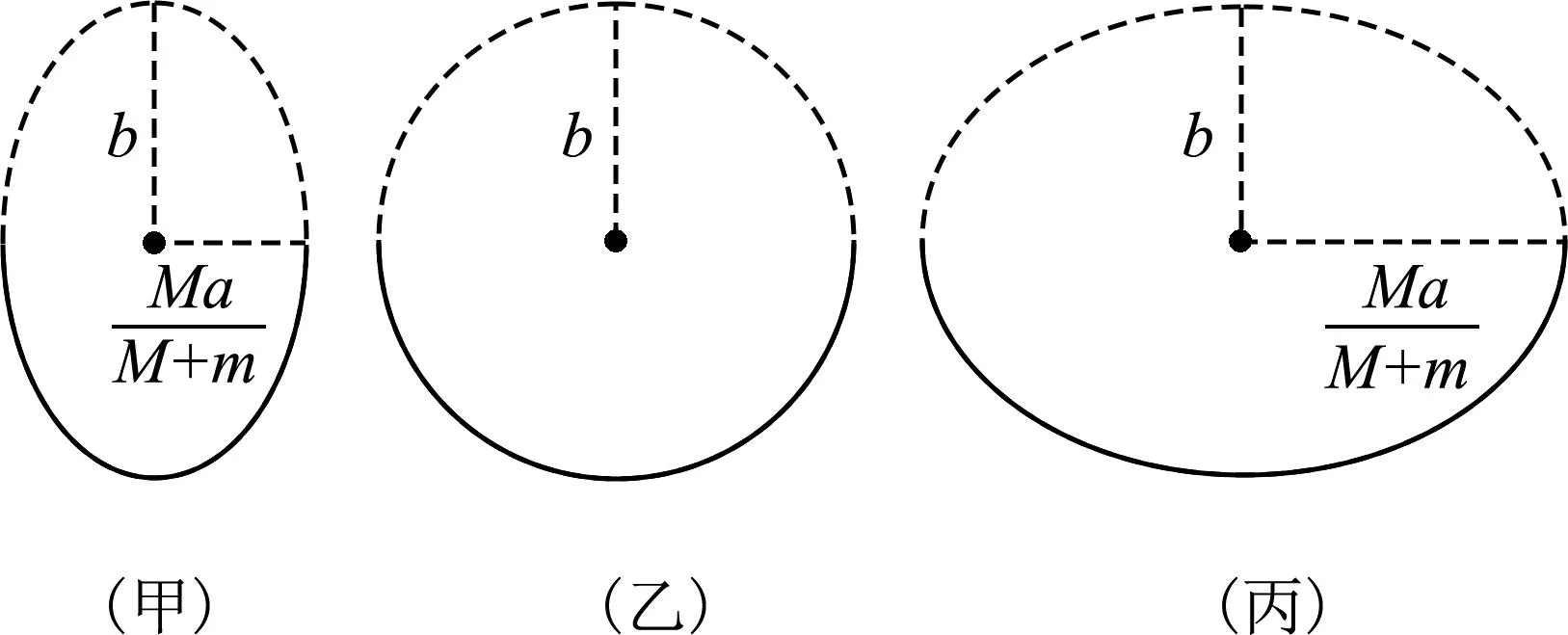
图2 小球运动轨迹

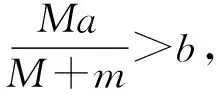
2.3 第(3)问解读

第(3)问是在给定质量比的条件下,求解特殊位置的状态量．虽然第(2)问用到了椭圆方程,对数学知识的要求较高,但由以上讨论可知,第(3)问通过设置槽球的质量比,恰巧可以将椭圆运动降解为圆周运动,从而降低对数学知识的要求,问题设计非常创新精妙．

方法1:简化为圆周运动确定速度方向.

[x-(a-b)]2+y2=b2,(y≤0).

(10)

由式(10)可知,在这种情况下小球的轨迹是以(a-b,0)为圆心,半径为b的半圆形．

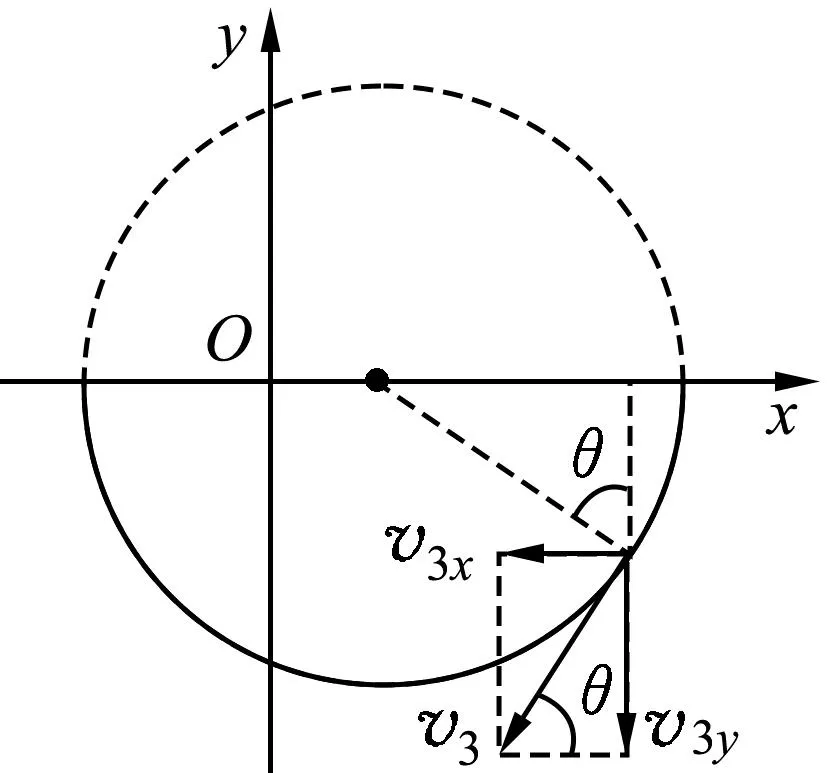
图3 小球速度分析

θ=60°.

(11)

由系统的水平方向动量守恒可得

mv3cosθ=Mv4.

(12)

由系统的机械能守恒可得

(13)

联立式(11)(12)(13)解得

(14)

从式(14)的结果来看,v3与水平方向的长半轴a和竖直方向的短半轴b均有关．从求解过程来看,关键是要确定小球的速度方向即可以迎刃而解．下面再给出两种方法得到式(11)的结果.

方法2:对椭圆方程求导确定速度方向.

将式(9)中的变量x和y分别对时间t求导可得

(15)

(16)

由式(16)同样可以确定小球速度与水平方向的夹角为

(17)

方法3:由椭圆切线斜率确定速度方向.

(18)

由式(9)确定y是x的隐函数,根据隐函数的求导法则可得

(19)

则以小球所在位置(x0,y0)为切点,代入式(19)可得运动轨迹的切线斜率为

(20)

(21)

方法点评:对比以上3种方法,方法1是高中范围内的常规方法,由于物理过程和轨迹方程都比较复杂,所给的质量比条件比较隐蔽,给学生造成不小的心理压力,但作为压轴题最后一问的精妙之笔,将“球槽模型”考到了极致,命题人的功力和手法可见一斑．方法2和方法3对于物理竞赛生更有优势,无须挖掘潜在条件中的半圆形轨迹形状,只要从一般的轨迹方程入手寻找速度关联即可,其中方法2的思维最直接,方法3需要求出切点的坐标和椭圆的切线斜率．

3 模型溯源

试题来源于物理竞赛题中的“球槽模型”,只是将通常的半圆形槽拓展为半椭圆形槽．原竞赛题大致为:如图4所示,质量为M的匀质凹槽放在光滑水平地面上,凹槽内有一个半圆形的光滑轨道,圆的半径为R．质量为m的小球(可视为质点),初始时刻从圆轨道的右端点由静止开始下滑．以初始时刻凹槽圆心的位置为坐标原点,在竖直平面内建立固定于地面的直角坐标系xOy,圆的直径位于x轴上,整个过程凹槽不翻转．求小球运动的轨迹方程．

图4 小球在半圆形凹槽中的运动

解析:小球在凹槽中运动的过程中,相对于凹槽做圆周运动,但相对于地面并不是圆周运动．设小球在坐标系xOy中的坐标为(x,y),则小球向左运动的水平位移为(R-x)．设凹槽向右运动的位移为x4,由式(4)可得

(22)

凹槽移动后的半圆形轨道方程为

(x-x4)2+y2=R2,(y≤0).

(23)

小球始终在凹槽半圆形轨道上,式(23)即为小球运动的轨迹方程,联立式(22)(23)解得

(24)

4 模型拓展

仔细考查可以发现,在上述“球槽模型”中并不限于特定的轨道约束,也可以改为轻绳或轻杆连接,变为如图5所示的“球环模型”,或如图6所示的“球车模型”等,它们的特点和实质相同．[1,2]从小球运动的轨迹形状来看,都可以称为“椭圆摆模型”,下面举例说明．

图5 球环模型

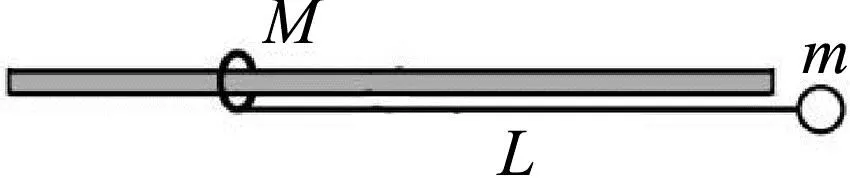
图6 球车模型

如图5所示,质量为M的圆环套在光滑固定的水平杆上,质量为m的小球用一根长为L的轻绳与圆环相连,小球和圆环均可视为质点．初始时刻轻绳与水平杆平行且处于拉直状态,圆环和小球均静止,现将小球由静止释放．以初始时刻圆环的位置为坐标原点,在竖直平面内建立固定于地面的直角坐标系xOy,轻绳水平拉直时位于x轴上．求小球运动的轨迹方程．

解析:在小球向下摆的过程中,相对于凹槽做圆周运动,但相对于地面并不是圆周运动．如图7所示,设小球在坐标系xOy中的坐标为(x,y),则小球向左运动的水平位移为(L-x)．设圆环向右运动的位移为x5,由式(4)可得

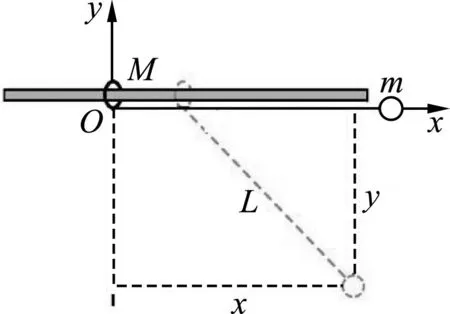
图7 小球运动分析

m(L-x)=Mx5,

(25)

由小球和圆环关联运动的约束条件可得

(x-x5)2+y2=L2,(y≤0).

(26)式(26)即为小球运动的轨迹方程,联立式(25)(26)解得

(27)

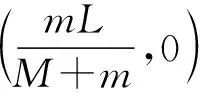
5 教学启示

从近些年全国各地的高考试题来看,物理竞赛题、大学物理和前沿科技的改编题不断地变相出现,特别是压轴题总能看到一些“影子”,这与新高考改革和高校选拔人才的要求是一脉相承的．因此在教学中,一方面要拒绝“题海战术”,减少重复低效的“机械刷题”行为,切实减轻学生负担;另一方面要强化模型建构意识,将题型归纳转变为模型建构,提升模型迁移能力,注重深度思维的培养,有效促进关键能力的提高,发展学生的物理核心素养．