非独立同分布场景下的联邦学习优化方法

宋华伟，李升起，万方杰，卫玉萍

（郑州大学网络空间安全学院，河南 郑州 450000）

0 引言

在互联网时代，全球数百亿的联网设备产生的数据呈指数级增长［1-2］。充分利用这些海量数据可以助力于建立更复杂、准确的神经网络模型［3］，提高神经网络模型的质量。然而，现实中的数据由于数据隐私、行业竞争等限制［4］，数据本身的整合存在巨大的阻碍，集中式训练的方式变得越来越不可行。

由于上述问题的出现，联邦学习（FL）得到了越来越多的关注［5］。联邦学习技术由谷歌于2016 年首次提出［6］，核心思想是在保护数据隐私的前提下，实现多方参与的训练，解决数据集中化和数据孤岛问题。联邦学习采用分布式的训练过程，客户端利用本地数据更新局部模型，无需上传本地数据，仅将更新后的局部模型参数上传到服务器，不断交互、更新执行，直到全局模型收敛或达到预定的训练轮数。联邦学习技术很好地平衡了大量数据、数据隐私与数据价值之间的矛盾。

但是，联邦学习拥有优势的同时也带来新的问题。联邦学习通常涉及大量客户端，这些参与方数据的独立同分布（IID）程度对模型训练的最终效果有重要的影响［7-8］。但在现实情况中，每个参与方的本地数据总是非独立同分布（Non-IID）的，例如：在医疗领域，不同的参与方可能拥有来自不同病人的医疗图像数据，数据在大小、颜色、对比度、亮度等方面均存在差异；综合性医院每种类型的数据可能都比较全面，而专科医院只有某一类的数据比较全面，且这一类数据的质量较高。因此，如何设计一个在数据Non-IID 下的联邦学习方法，实现更好的学习效果，对联邦学习的发展和应用具有重要的现实意义，同时也是本文研究的问题。

为了解决Non-IID 数据场景下模型准确率下降的问题，相关学者进行了一系列的研究。ZHAO等［9］的研究表明，在CIFAR-10 数据集中只需共享5%的数据子集就能够提高30%的准确率，但是共享数据可能会泄露数据隐私。LI等［10］给模型的目标函数加上一个限制项，用于限制局部模型和全局模型的差异，以此来减小数据异构带来的影响，然而，FedProx相较于FedAvg 提升 较为有限。WANG等［11］考虑了参与方可能在每轮需要执行不同数量的局部步骤，因此，为了确保全局更新没有偏差，在全局聚合之前对其每一方的局部更新进行归一化和缩放，消除目标不一致性，保持全局模型快速大幅度收敛。文献［12］采用集群学习方式将具有相似分布的参与方聚集到固定的簇中，并为不同簇训练不同的全局模型以适应其固有数据分布，但这种方式得到的全局模型泛化性能差。FedFa［13］将客户端模型的准确率和选中次数作为本地数据质量的衡量标准，并为每个客户端赋予相应的聚合权重。

另一个研究方向是将一些技术融入联邦学习，诸如多目标学习［14-15］、元学习［16］、持续学习［17］、对抗学习［18］、区块链［19-20］等技术被广泛应用于Non-IID 联邦学习场景中。其中一个很好的研究方向是将持续学习应用于联邦学习领域。SHOHAM等［21］基于联邦学习与持续学习的类比，将灾难性遗忘的解决方案应用于非独立同分布数据下联邦学习存在的局部模型漂移问题。FedLSD［22］侧重于本地更新学习到的知识，通过蒸馏获取全局模型的知识。这些方法减少了数据异质带来的影响，但是不同客户端数据分布不同，学习到的知识也存在差异，全局模型聚合时仍会存在差异的干扰。

基于上述研究成果不难发现，数据非独立同分布下的联邦学习优化方法可以从全局模型聚合和本地客户端更新两个角度加以改进。但大多数方法都是在一个角度进行优化，难免不会引发另一角度带来的影响，降低全局模型的质量。针对这种现象，本文提出了分层持续学习的联邦学习优化方法（FedMas）。在FedMas 中，将数据非独立同分布导致的全局模型准确率低的问题建模为持续学习任务。考虑一个极端的例子：假设有10 个参与方，每个参与方拥有MNIST 数据集的其中一类的全部数据，采用联邦平均算法［6］进行训练，每次全局模型聚合都会因权重发散导致准确率低，但如果用持续学习的灾难性遗忘的解决方案去训练，则可以融合不用任务的特征，提高全局模型的准确率。

FedMas 将参与方根据其数据分布特征划分逻辑层，单个层中的参与方的数据分布相似，避免随机抽取时由于数据分布不同导致权重发散、准确率降低的问题，推动全局模型训练更快地收敛。由于层间数据分布不同，为了学习不同数据分布的特征，本文采用持续学习算法-记忆感知突触算法［23］融合不同数据间的差异性。简言之，FedMas 算法通过聚类分层减少不同数据分布客户端聚合时的干扰，通过记忆感知突触算法持续学习有益的全局知识，以最大化提高全局模型的收敛速度和模型质量。

1 分层持续学习的联邦学习方法

1.1 问题描述

在联邦学习场景中，全局服务器和参与方通过网络连接，模型训练使用的训练数据是分散在各个边缘设备上的，通过迭代的全局聚合和更新来实现模型的训练。联邦学习的优化目标是最小化所有样本的平均损失，如式（1）所示：

Fk(w)代表了局部数据的分布信息，当所有的参与方都是独立同分布的时候，可以得到式（2）：

即当客户端上的数据与总体数据分布相同时，客户端上的预测损失应与全局的预测损失期望相同，通过多次同步后，其聚合后的全局模型能够逼近集中式训练的模型；而当数据不满足独立同分布假设时，模型拟合自身所持有的数据集，造成参数方向的分歧，并且随着同步的次数增多，分歧越来越大，在服务器端聚合时偏移全局最优解，如图1 所示。

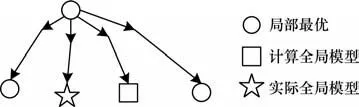
图1 Non-IID 数据训练时的模型偏移Fig.1 Model offset during Non-IID data training

在上述方法的基础上，本文提出了FedMas 方法。FedMas 将整个过程分为两个部分：按数据分布对客户端分层，以及对不同层进行知识融合。FedMas 的整体架构如图2 所示，算法描述见算法1。

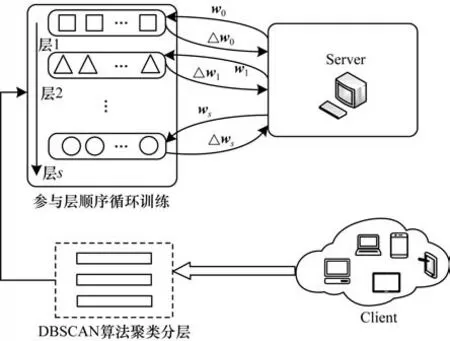
图2 FedMas 整体架构Fig.2 Overall architecture of FedMas

算法1FedMas

1.2 客户端分层

数据分布不同的客户端在聚合时会受到其他客户端学习知识的干扰。为了避免这个问题，本文将所有客户端进行了分层。文献［12］为每个层训练一个全局模型，这样做的后果是不能很好地利用联邦学习维持的大规模数据集的优势，数据量少的客户端容易过拟合，因此，本文对聚合的层进行了知识融合。分层的具体过程如下：

在服务器端初始化一个全局分类模型，并将全局模型广播至所有客户端对本地数据的样本进行e轮次的本地训练，每个客户端利用本地的数据集按式（3）进行参数更新：

其中：η是学习率；xi是客户端的数据样本；ℓ(w0；xi)为参数w0的损失函数的梯度。

训练结束后，客户端上传本地模型参数到服务器端。因为更新之前的模型参数相同，更新过程中只有数据不同，所以得到的新的模型参数仅仅包含了客户端的数据分布信息。采用DBSCAN 聚类［24］方法对收集到的模型参数进行聚类，将客户端划分到不同的层Tier 中，聚类分层后，每个层中客户端的数据分布相似（见算法1 中的第1～4 行）。

1.3 持续学习

如何融合不同层的知识是本文算法分层后要解决的关键问题，持续学习为解决这个问题提供了很好的思路。持续学习可以在学习后一个任务时不忘记前一个任务学习的知识，经过不断的发展已经取得不错的成果，其中记忆感知突触算法是一个成功的方法。同样作为基于正则化的方法，和弹性权值合并算法相比，记忆感知突触算法的重要性权重矩阵获取方式能够从无标签数据中学习，这个属性使得该方法能够应用在没有训练数据的场景下并且其占用的内存更小。因此，记忆感知突触算法更适合用于联邦学习场景。记忆感知突触算法通过计算网络模型中每个参数对于该任务的重要性，并沿用到训练后续的任务的方式，以保持对原数据集较好的分类性能。记忆感知突触算法损失函数如式（4）所示：

其中：Ln(w)为新任务（第n个任务）的损失函数损失函数；Ωij表示每个参数对于该任务的重要性；是由前n-1 个任务训练后得到的模型，同时也是用于训练第n个任务的初始模型的参数；λ为一个正则项的可调的超参数。

此外，式（4）中Ωij为重要性权重矩阵，原作者使用L2 范数的平分的偏导代替，具体如式（5）所示：

1.4 局部持续学习

本文将Non-IID 数据学习问题建模为持续学习任务，考虑到Non-IID 场景下聚合权重发散以及持续学习任务之间的顺序性，本文没有将每个边缘设备视为一个单独的学习“任务”，而是设计了FedMas，将具有相似原型的设备分组在一起，并将每组设备视为学习任务。

FedMas 算法需要执行C个通信轮次，在每个通信轮次内所有层按序参与训练，每个层训练时只随机抽取层内的一部分客户端，并采用加权聚合更新全局模型。在Tier 中第一次选取层训练时，因为全局模型为初始化参数，所以损失函数为交叉熵损失，不加入记忆感知突触算法项，损失函数如式（6）所示：

其中：n为训练集的样本大小；y为训练数据的标签向量；a为神经网络模型的输出向量。

从第2 次选择层训练开始直到训练结束，客户端接收到的模型来自上一层，模型在本层训练时参数的变动可能会覆盖神经网络在旧数据上所学的知识。为了缓解这个问题，本文在本地训练时引入记忆感知突触算法，通过尽量减少旧任务上重要参数的改变幅度，以期同时在不同任务上取得良好的效果。损失函数为交叉熵损失和记忆感知突触算法项的和，如式（4）所示。记忆感知突触算法的Ωij项一般是在旧数据集上进行计算，考虑到联邦学习的旧数据集在上层的多个客户端上，每个层的客户端数据分布类似，本文采用随机抽取一个客户端的方式更新Ωij，具体过程见算法1 中的第5～24 行。

FedMas 算法的主要思想是通过聚类分层减小层内权重分歧的影响，同时通过引入记忆感知突触算法聚合层间的知识，减小Non-IID 数据对全局目标函数的影响，提高训练质量。

2 实验结果及分析

2.1 数据集和模型

实验使用MNIST 和CIFAR-10 数据集，具体如下：

1）MNIST 数据集。MNIST 数据集有10 个不同类别的手写体数字（数字0～9），其中，训练集包含60 000 张图片和标签，测试集包含10 000 张图片和标签。在MNIST 数据集上使用由1 个卷积层、1 个最大池化层、3 个全连接层组成的神经网络模型。

2）CIFAR-10 数据集。CIFAR-10 数据集包含60 000 张32×32 像素的彩色图像，其中，训练集包含50 000 张图像，测试集包含10 000 张图像。CIFAR-10数据集图像共有10 个类，分别为飞机、汽车、鸟类、狗等，该数据集更复杂，学习的难度更大。在CIFAR-10 数据集上使用由2 个卷积层、2 个平均池化层和2 个全连接层组成的卷积神经网络模型。

2.2 实验设置

为了体现FedMas 算法在数据异质环境下的特点和性能，将其与目前表现较好的联邦学习算法FedProx［10］、Scaffold［25］和FedCurv［21］进行对 比，实 验结果将在2.4 节中讨论。FedProx 算法基于FedAvg改进了局部目标，引入了一个附加的近端项，用于限制局部模型和全局模型的差异，FedProx 的超参数mu 按照原文选择0.2。Scaffold 算法引入了控制变量纠正Non-IID 数据局部训练时的漂移问题。FedCurv 和FedProx 很类似，只是把正则化项改为EWC 算法的正则化项，通过持续学习正则化项克服数据异构下联邦学习的灾难性遗忘，FedCurv 在原文中λ=2.0 时效果更好，因此，在本文中设定λ=2.0。对于FedMas 算法的超参数λ，如果设置得过小，则对局部更新没有影响；如果设置得过大，模型更新很慢，参考FedFMC［26］的设置方式，设为

为了更符合真实情况，本文通过狄利克雷分布来模拟不同客户端数据集标签倾斜的Non-IID 分布。根据狄利克雷分布划分而来的数据集分布情况受狄利克雷的参数α控制［27］：α越大，所得到的概率分布越逼近均匀分布，采样所生成的数据集越趋向于独立同分布；α越小，所得的概率分布越偏向于集中某一些点，数据集的偏斜越严重，所得数据集越近似Non-IID 数据集。本文分别在α=0.3和α=0.7 取值下对MNIST 和CIFAR-10 这两个数据集进行随机采样，产生Non-IID 程度不一致的数据集并随机分发给各个客户端进行实验，以此评估FedMas 在处理不同程度的Non-IID 数据时的表现。以MNIST 数据集为例，在不同的异构设置下，取前10 个客户端，其本地数据分布如图3 所示（彩色效果见《计算机工程》官网HTML 版）。

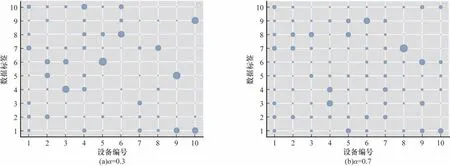
图3 MNIST 数据集在不同异构设置下前10 个客户端的数据分布图Fig.3 First ten clients' data distribution in MNIST dataset under different data heterogeneities

在本地训练中，使用的优化器中SGD 参数设置为：学习率0.01，本地训练轮次为5 轮，对比实验中MNIST 数据集 通信轮次为50 轮，CIFAR-10 数据集通信轮次为100 轮，客户端总数为100 个，每次以0.2的样本率对客户端进行随机抽样，样本输入维度为64，batch 大小设置为10。模拟实验在同一台具有NVIDIA RTX A5000 24 GB 的机器上进行。

2.3 消融实验

FedMas 整体可分为2 个部分：1）将数据分布相似的客户端划分到一个层；2）在本地客户端局部更新时加入记忆感知突触算法项。为了验证这种分层持续学习的联邦学习优化方法的有效性，对上述两个部分的有效性分别进行消融实验。为了更清晰地了解数据非独立同分布性质的干扰，采用MNIST 数据集进行实验，该数据集共有10 类，将每个类别的数据平均分给其中的10 个客户端，通信轮次为200 轮，其余实验相关参数设置不变，分别以FedAvg算法（FedAvg）、结合记忆感知突触算法项的FedAvg算法（FedAvgMas）、对客户端进行分层的FedAvg 算法（TFedAvg）和对客户端进行分层并结合记忆感知突触算法的FedAvg 算法（TFedAvgMas）进行实验，结果如图4 所示。

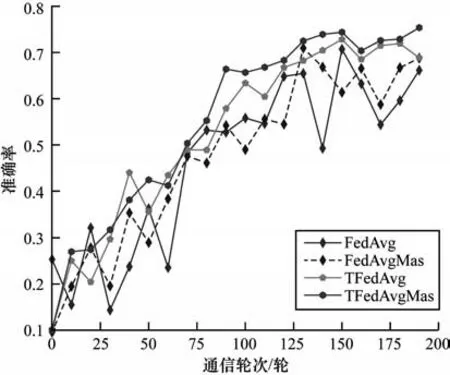
图4 分层和局部更新的有效性Fig.4 Effectiveness of hierarchical and local updates

1）分层策略的有效性。分层策略考虑了数据分布不同的客户端在聚合时会受到其他客户端学习知识的干扰。图4 中FedAvg 和FedAvgMas 没有分层，采用的是FedAvg 算法的随机挑选策略，TFedAvg 和TFedAvgMas 采用了客户端分层策略。可以看出：在MNIST 数据集下，采用客户端分层策略的TFedAvg和TFedAvgMas，其平均准确率比随机挑选的方案提升了近5 个百分点；在前80 轮通信过程中，4 种策略的平均准确率较为接近，但是TFedAvg 和TFedAvgMas 的提升过程更为平稳；在其他通信轮次，分层策略的平均准确率几乎全部优于随机挑选策略；此外，随机挑选策略相较于分层策略的训练曲线始终存在较大的波动。实验结果表明了分层策略在数据非独立同分布下的有效性，分层策略可以避免因随机挑选带来的全局模型聚合时多个客户端数据分布不同的相互干扰，且分层后每个轮次可以学习全部数据分布客户端的丰富知识，稳步提升全局模型的性能。

2）局部更新策略的有效性。在MNIST 数据集下，加入了记忆感知突触算法项策略的平均准确率较未加入的方案提高了1 个百分点；FedAvg 与FedAvgMas 以及TFedAvg 与TFedAvgMas 的对比结果表明，使用记忆感知突触算法项可以通过缓解局部模型训练时的灾难性遗忘进一步提升全局模型的性能。

2.4 对比实验效果

表1 展示了FedMas 和其他方法在不同Non-IID程度数据集上准确率比较的结果，其中加粗表示最优值。从实验结果来看：结合了持续学习算法的FedCurv 算法和FedMas 算法在不同的数据集以及数据异构情况下，比FedProx 算法和Scafflod 算法得到一个更好的全局模型；Scafflod 算法在特征分布更为复杂的CIFAR-10 数据集比FedProx 算法优势更明显；Non-IID 程度越高时，FedMas 算法的效果与其他算法准确率差距越大，这说明本文提出的算法能有效避免数据非独立同分布的干扰，充分学习不同数据分布之间的知识，获得更好的分类效果；当数据Non-IID 程度低时，FedMas 算法和其他算法效果差距减小，但持续学习算法的优势在于即便是在独立同分布的数据场景下使用，神经网络训练时仍能因其抗遗忘特性而提高模型的质量。因此，FedMas 在联邦学习中优势更加明显。

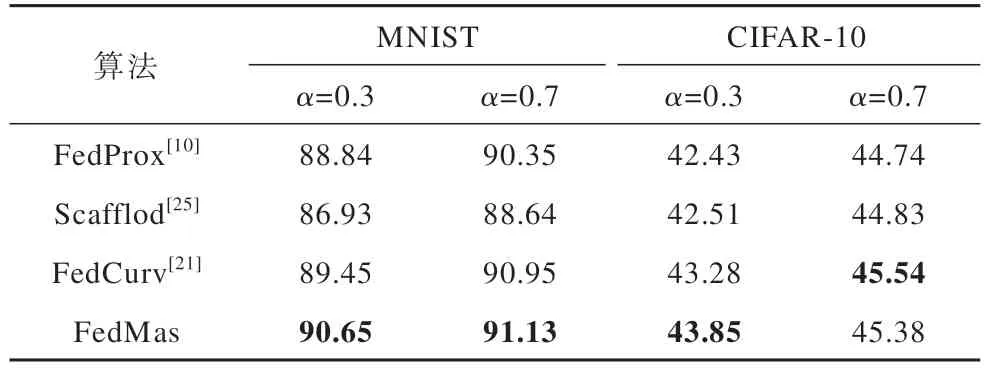
表1 不同Non-IID 程度下的准确率比较Table 1 Accuracy comparison under different Non-IID levels %

各算法在α=0.3 时准确率随训练轮次的变化趋势如图5、图6 所示，可以看出：本文提出的算法具有更快的收敛速度，最终准确率也最高，证明了提出模型的有效性；FedMas 算法每次局部更新时利用重要性权重矩阵限制了学习到知识的参数的更新程度，相较于其他算法每次变化更稳定，准确率更高；FedProx 算法和Scafflod 算法在学习的过程中波动较大，其中Scafflod 算法在MNIST 数据集上波动比较大，在CIFAR-10 数据集相对稳定，并且性能较好。

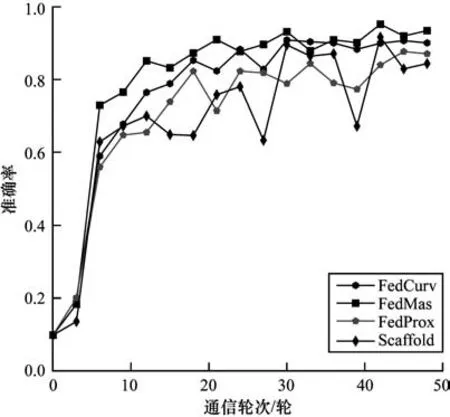
图5 α=0.3 时FedCurv、FedProx、Scaffold 和FedMas 在MNIST 数据集上的准确率Fig.5 The accuracy of FedCurv，FedProx，Scaffold and FedMas on the MNIST dataset when α=0.3

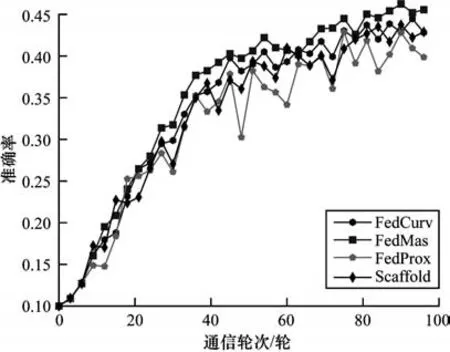
图6 α=0.3 时FedCurv、FedProx、Scaffold 和FedMas 在CIFAR-10 数据集上下的准确率Fig.6 The accuracy of FedCurv，FedProx，Scaffold and FedMas on the CIFAR-10 dataset when α=0.3

3 结束语

本文为非独立同分布场景下的联邦学习提供了一种新方法，它建立在全局聚合和局部更新的解决方案之上。该方法通过关注客户端的数据分布情况对其进行分层，将每个层建模为持续学习的任务，再对层进行抗遗忘的知识融合学习，得到最终的预测模型。在不同数据集上和其他模型的对比结果，证明了本文方法的有效性。本文方法架构考虑到真实场景中的客户端数据异质情况，因此具有一定的普适性，可应用在多客户端共同训练的场景下。在未来工作中，将关注因硬件设施导致的掉队设备给实验带来干扰，以及客户端设备异构的问题，设计性能更好的联邦学习算法。