基于粒子群优化算法的电弧增材制造焊道尺寸反向传播神经网络预测模型
刘浩民,杨洪才,刘 战,李子葳,孙俊华,张元彬
(1.山东建筑大学材料科学与工程学院,济南 250101;2.山东济容热工科技有限公司,济南 250199)
0 引 言
从20世纪80年代开始,增材制造技术迅猛发展,应用领域也愈加广阔。增材制造技术以计算机辅助设计/计算机辅助制造(CAD/CAM)为基础,采用逐层堆积的方式来进行零件成形[1]。金属材料增材制造技术根据热源类型的不同可分为激光增材制造、电子束增材制造、电弧增材制造等。激光增材制造技术和电子束增材制造技术由于设备运转维护成本较高,在制造大型复杂构件时有一定的局限性[2]。电弧增材制造材料利用率高,可实现多种材料混合制造以及大尺寸复杂构件低成本、高效快速近净成形,在成形过程中只需局部保护无需密封仓保护(部分金属除外)[3-5],并且采用电弧增材成形技术制造的金属构件化学成分均匀,组织致密,具有优良的力学性能[6]。
良好的焊道成形是电弧增材制造的基础。建立不同焊道尺寸预测模型,进而得到不同增材制造工艺参数下的焊道成形尺寸,是进行电弧增材制造的有效保障[7-8]。胡建文等[9]将送丝速度、焊接速度、焊接电压和喷嘴高度作为模型输入变量,将焊道熔宽和余高作为输出变量,比较了二次回归模型及神经网络模型的预测能力,结果表明后者的预测精度更高。黄无云等[10]对4-12-2结构的反向传播(BP)神经网络模型的权值进行了优化,结果表明优化模型可以准确预测单条焊道成形尺寸。王晓光等[11]研究发现,在电弧增材制造316L奥氏体不锈钢单道多层薄壁件的过程中,成形宽度随着焊接速度的减小而增大,侧面成形误差、沉积效率随着热输入增加分别呈先减后增、先增后减的变化趋势。CHUAIPHAN等[12]研究发现,在焊接电流为75 A、焊接速度为2.0~3.5 mm·s-1下电弧增材制造304不锈钢焊道的成形良好。SADA等[13]研究表明,将焊接电流、电弧电压、送丝速度作为输入变量,将焊道截面尺寸作为输出变量建立的焊道截面尺寸预测模型的可靠性系数大于80%,其中焊接电流对焊道截面尺寸的影响最为显著。SAFARI等[14]对粒子群优化(PSO)算法及遗传算法(GA)的性能进行比较发现,粒子群优化算法预测更快更有效,能在更少的迭代次数中得到目标值。虽然目前电弧增材制造技术得到了飞速发展,但仍然存在许多问题亟待解决,例如焊道成形尺寸预测、零件整体成形精度等。相较于传统BP神经网络权值的随机赋值,粒子群优化算法可以搜索到BP神经网络的最优权值,其搜索能力取决于其全局探索以及跳出局部最优的能力,这在很大程度上依赖于算法控制参数的选择。
为此,作者针对熔化极惰性气体保护(MIG)电弧增材制造316L不锈钢工艺,选取焊接电流、送丝速度、焊接速度及基板温度作为输入变量,焊道熔宽和余高作为输出变量,通过合理选择粒子群优化算法中的粒子惯性权重和学习因子,构建了PSO反向传播(PSO-BP)神经网络模型,并进行焊道尺寸预测和精度验证,以期为焊道尺寸的精准预测和零件的整体成形提供理论基础。
1 试验方法与结果
焊接材料为316L不锈钢焊丝(直径为1.2 mm),基板为304不锈钢板(尺寸为200 mm×200 mm×6 mm),化学成分(质量分数/%)见表1。基板表面经打磨、去污后,采用FANUC M-10iD型六轴焊接机器人、Pulse MIG-350RP型焊接电源搭建MIG电弧增材制造试验平台,焊枪与工作台保持垂直,焊枪喷嘴与基板间距为15 mm,焊接电流为110~170 A,焊接速度为2~6 mm·s-1,送丝速度为2.8~5.3 m·min-1,保护气体为高纯氩气(纯度为97.5%),流量为15 L·min-1;焊接电流、送丝速度、焊接速度及基板温度对焊道成形影响显著,因此选取这4个工艺参数为焊道尺寸BP神经网络模型的输入变量,焊道熔宽和余高作为输出变量。将焊接单条焊道前的基板实时温度作为焊接该条焊道的基板温度,在当前焊道焊接结束后采用红外线测温仪测定第一焊道焊接的起始温度。为了减少预热搬运过程中的热量损失,将室温下基板中的第一条焊道焊接过程作为基板预热的过程,不将该焊道纳入BP神经网络预测模型。

表1 304不锈钢板和316L不锈钢焊丝的化学成分Table 1 Chemical composition of 304 stainless steel plate and 316L stainless steel welding wire
电弧增材制造时电流大小和热输入有关,焊接速度和送丝速度会影响焊丝的熔覆效果,因此小电流采取较小的送丝速度及焊接速度,大电流采取较大的送丝速度和焊接速度。选取焊道形貌均匀的3个点,采用千分尺测量其对应熔宽及余高,精度为0.02 mm,取平均值。去除室温下基板的第一条焊道数据后94组工艺参数及其对应的焊道成形尺寸数据,随机选取70组数据作为训练集数据,剩余24组数据作为测试集数据用来测试BP神经网络模型的精度,部分数据如表2所示。
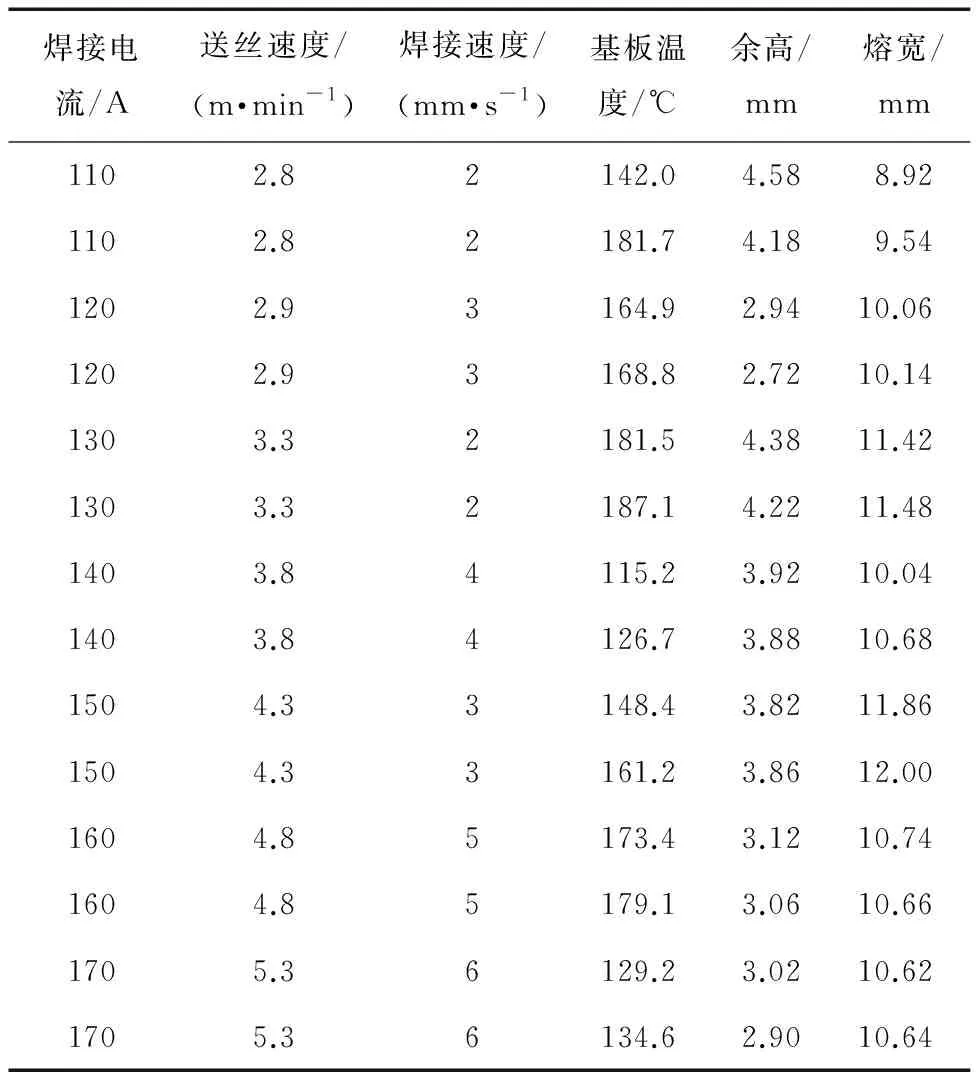
表2 BP神经网络模型部分工艺参数及其对应的焊道尺寸Table 2 Part process parameters and their corresponding weld size of BP neural network model
2 BP神经网络模型的建立
采用三层BP神经网络结构,如图1所示,输入层由焊接电流、焊接速度、送丝速度和基板温度4个神经元构成,输出层包括焊道熔宽和余高2个神经元,隐藏层神经元个数的经验公式[15]为
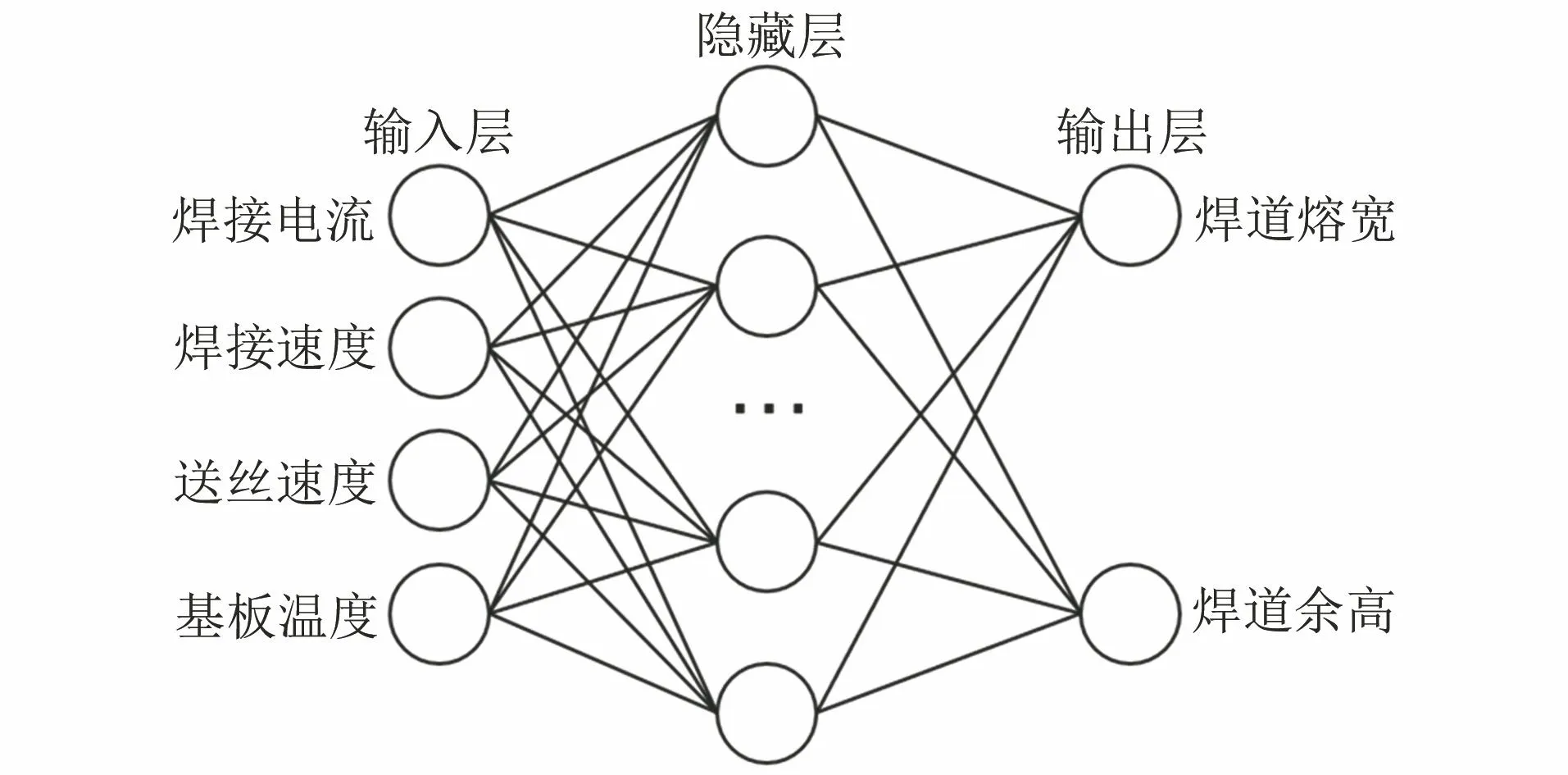
图1 BP神经网络模型结构Fig.1 BP neural network model structure
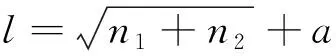
(1)
式中:l,n1,n2分别为隐藏层、输入层、输出层的神经元个数;a为1~10的常数。
根据式(1)可得隐藏层的神经元个数为3~12。隐藏层神经元个数会影响预测效果,通过比较不同隐藏层神经元个数下的网络性能(输出值与期望值之间的均方误差),得出预测模型最佳的隐藏层神经元个数为12,即该BP神经网络预测模型为4-12-2的结构。
BP神经网络每层之间均具有激活函数和连接权值,为了解决非线性模型问题,加入非线性因素,选择Sigmoid函数作为隐藏层激活函数,计算公式如下:
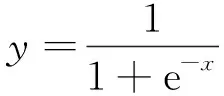
(2)
式中:x为隐藏层输入值,可以取任意实数;y为隐藏层输出值,取值范围在(0,1)。
在模型训练前,统一对样本使用Mapminmax函数进行归一化处理以减少个别样本对训练的影响,使数据在[-1, 1]的取值范围内。在输出数据之前,需要对其进行反归一化以确保输出值真实有效,该归一化函数为

(3)
式中:x为样本数据,是BP神经网络的输入数据或期望输出;xmax,xmin分别为所有样本数据中最大值与最小值;y为对x归一化处理后得到的数据;ymin,ymax为归一化参数,默认为-1和1。
3 粒子群优化算法优化权值
粒子群优化算法是一种进化计算技术,基本理念是通过个体之间的协作以及群体中的信息共享来寻求最优解。采用粒子群算法的迭代寻优找到最优权值,代替BP神经网络中的初始化权值,从而提高模型对焊道尺寸的预测精度,具体流程如图2所示。

图2 粒子群优化算法优化BP神经网络权值阈值流程Fig.2 Flow chart of optimizing BP neural network weight threshold by particle swarm optimization
3.1 随机初始化粒子群
定义粒子群优化算法时,需要粒子的位置X和初始化速率V,两者算法分别为
X=-5+10×rand(P,N)
(4)
V=2×rand(P,N)
(5)
式中:P为粒子群中粒子的数目;N为目标函数自变量个数。
3.2 计算粒子的适应度
粒子群优化算法中适应度函数的选择很重要,采用BP神经网络预测的输出值与期望值之间差值矩阵的模作为适应度函数,公式为
Err=norm(A-B,2)
(6)
式中:A为输出值矩阵;B为期望值矩阵。
3.3 粒子群更新
在未满足粒子群寻优的终止条件时,粒子群会进行一次次迭代,每次迭代后都会对当前粒子的速率Vi、位置Xi,存储个体最优pbesti和存储全局最优gbesti进行更新,更新公式为

(7)

(8)
式中:W为惯性权重,影响粒子继承上一次迭代速度的比重;C1,C2分别为个体学习因子和社会学习因子,均为常数;R1,R2为[0,1]间的随机数。
在粒子群优化迭代前期,粒子应当采取较大的惯性权重以便进行粒子全局搜索,确定范围;后期应采用较小的惯性权重,以便精确锁定全局最优的位置。惯性权重采用线性递减原则,从最大惯性权重Wmax逐渐递减至最小惯性权重Wmin,权重公式为

(9)
式中:k为当前迭代次数;nmax为最大迭代次数。
减小C1,可以加强粒子初期的全局搜索能力,避免在搜索初期出现粒子陷入局部范围;增大C2,可以避免搜索过程中粒子出现过早的局部收敛,加强粒子后期的局部搜索能力[16]。学习因子公式分别为
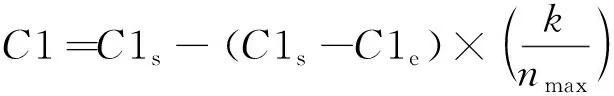
(10)
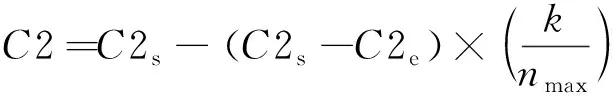
(11)
式中:C1s,C1e分别为C1的开始值和结束值;C2s,C2e分别为C2的开始值和结束值。
3.4 BP神经网络权值更新
连接权值关系到BP神经网络训练速率的快慢以及收敛速率,在基本的BP神经网络中权值是随机设定的,在网络训练的过程中沿着误差减小的方向不断进行调整。针对连接权值的随机性、不确定等缺点,采用PSO对其进行优化。为了记录粒子寻优轨迹,引入trace0公式,为
trace0=zeros(M+1,nmax)
(12)
式中:trace0为记录粒子寻优结果的轨迹;M为待优化变量个数。
在粒子群算法迭代寻优结束后,trace0的最后一列中保存了寻优结果。为了保存最终寻优结果,即BP神经网络更新后的权值,引入保存公式,为
bestX=trace0(1:end-1,end)
(13)
式中:bestX为寻优轨迹中保存的BP神经网络更新后的权值;end为trace0表格的最后一行或者列。
为了提高预测模型的准确性,在对粒子群优化算法参数进行多次调整后得到最优参数:粒子数量为100个,最大惯性权重为0.9,最小惯性权重为0.4,粒子学习因子C1s,C1e,C2s,C2e分别为2,1,1.5,2,粒子群最大迭代寻优次数为70次。
4 模型训练及精度验证
首先设置BP神经网络训练参数: 训练精度为0.001,学习率为0.01,最大训练次数为1 000次。由图3可见, 在迭代寻优次数为35次时,适应度曲线趋于平稳,适应度值为1.15,即寻找到经PSO优化后BP神经网络模型(PSO-BP神经网络模型)的最佳权值。选用均方根误差(RMSE)作为PSO-BP神经网络模型的评价标准,用以衡量预测值和期望值的偏差,计算公式为

图3 PSO-BP神经网络模型权值寻优过程的适应度曲线Fig.3 Fitness curve of PSO-BP neural network model weight optimization process
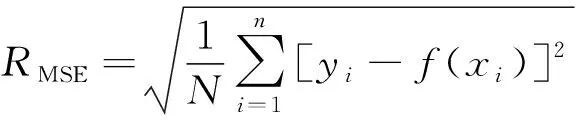
(14)
式中:yi为试验的期望值;f(xi)为PSO-BP神经网络模型输出的预测值;i为1~N之间的整数,N为样本个数。
由图4可见,BP神经网络模型的焊道熔宽预测相对误差分布散乱,虽然大部分样本相对误差很小,但有6个样本的相对误差较大,而PSO-BP神经网络模型对焊道熔宽和余高的预测相对误差分布集中并均较小,说明其预测值更加稳定更贴合期望值。

图4 不同神经网络模型的焊道尺寸预测值与期望值的相对误差Fig.4 Relative errors of predicted vodues weld bead size obtained by different neural network models and expected values: (a) weld width and (b) weld reinforcement
由表3可知,BP神经网络模型得到的焊道熔宽及余高预测值与期望值的均方根误差、相对误差均大于PSO-BP神经网络模型,PSO-BP神经网络模型除了个别样本的最大相对误差达到13.477%外,其他均维持在10%以内,集中在5%左右。综上所述,相较于BP神经网络模型,PSO-BP神经网络模型对焊道尺寸的预测精度更高更加稳定,可以应用到电弧增材制造中以提高成形件的精度。
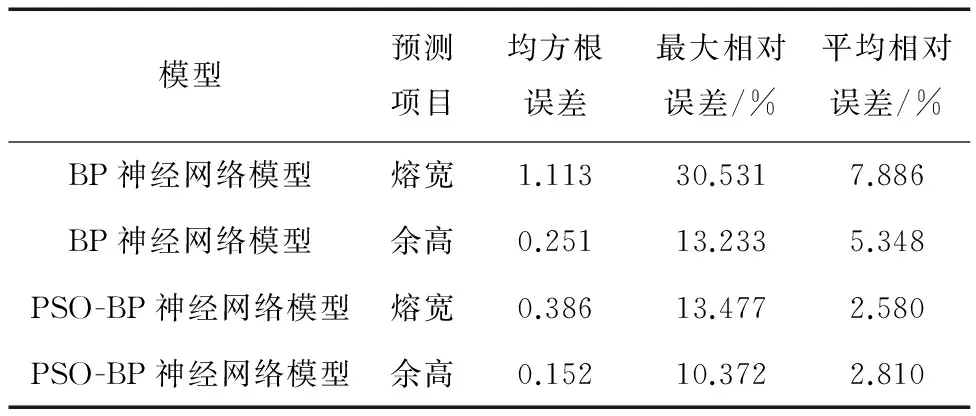
表3 不同神经网络模型对焊道尺寸的预测误差Table 3 Prediction error of weld bead size by different neural network models
5 结 论
(1) 针对熔化极惰性气体保护电弧增材制造316L不锈钢,选取焊接电流、送丝速度、焊接速度及基板温度作为输入变量,焊道熔宽和余高作为输出变量,选择粒子群优化算法(PSO)中的最优粒子惯性权重和学习因子,构建4-12-2结构PSO-BP神经网络模型。
(2) 采用PSO-BP神经网络模型预测的焊道熔宽与期望值的均方根误差、最大相对误差和平均相对误差分别为0.386,13.477%,2.580%,焊道余高的分别为0.152,10.372%,2.810%。相较于BP神经网络模型,PSO-BP神经网络模型对焊道尺寸预测精度高、效果好,稳定性强。

