一类抛物型方程初值与源项同时反演问题的唯一性与数值计算

阮周生，万广红，陈振兴

（东华理工大学理学院，南昌 330013）

0 引言

抛物型偏微分方程是一类被广泛用来刻画守恒现象的方程，在地下水污染的预防与治理、血液内部药物溶度扩散的预测、热场中温度分布的计算及传染病的预测与防护等实际问题中有重要的应用［1］。在利用抛物型偏微分方程描述具体现象时，往往系统中存在某些不明确或不易得到的信息，这些未知信息通常需要通过其他的附加信息来重构或反演，数学上将这类问题归结为抛物型微分方程反问题。抛物型微分方程初值反问题、源项反问题是2类典型的反问题，一直受到众多学者的关注，如文献［2－6］分别采用吉洪诺夫正则化、同伦分析方法、卷积正则化方法、截断正则化方法及拟边值正则化方法考虑了抛物型方程初值反问题；文献［7－9］分别采用基于变分伴随的梯度优化方法、算子半群方法及深度学习方法研究了抛物型方程仅与空间变量有关的源项反问题。针对初值与源项联合反演问题，文献［10－11］基于2个终止时刻的观测数据或一个终止时刻的观测数据附加边界上一段时域内的观测数据，分别采用拟逆法、最优化方法考虑了初值与源项同时反演问题。以上文献对初值反问题、源项反问题或同时反演问题的研究所附加的终止时刻观测数据为空间区域全局数据，从实际应用角度看，空间全局观测数据的获取往往比较困难，通常只能获得局部观测数据。最近，文献［12－13］从实际应用角度出发，基于稀疏观测数据，利用Laplace变换、解析延拓研究了一类抛物型方程逆时反问题和源项反问题的唯一性。文献［12］基于局部观测数据仅考虑了抛物型微分方程源项反问题，受文献［12］的启发，考虑如下抛物型方程同时反演问题：

同时反演问题考虑含局部区域3个不同时刻的观测数据gi（x），x∈Ωi⊂Ω，i＝1，2，3来同时反演源项f（x）与初值u0（x），即附加数据为：

式中：Ω0为Ω的子域，Ti，i＝1，2，3为3个不同的观测时刻，满足：T1＜T2＜T3。

1 同时反演问题的唯一性

由于－Δ为一致椭圆型算子，故存在可数的特征值，不失一般性，记为，满足λ1≤λ2≤…。记φi（x）为相应的规范特征函数，即有－Δφi＝λiφi（x），i＝1，2，…。下面先证明基于2点终止时刻的局部观测数据同时反演问题的非唯一性。

1.1 局部区域2个观测时刻附加数据下同时反演问题的非唯一性

利用特征函数展开法，式（1）的级数形式解可表示为：

式中：u0，i＝＜u0（x），φi（x）＞，fi＝＜f（x），φi（x）＞为相应初值和源项的傅里叶系数，i＝1，2，…，符号＜·，·＞代表函数内积。显然有

构造如下辅助问题：

同理可得上述问题（5）的解为：

故，当g1（x）＝g2（x）＝0时，有

1.2 含局部区域3个观测时刻附加数据下同时反演问题的唯一性

下面给出基于局部区域3个观测时刻数据下同时反演问题的唯一性结论。

定理1设，则局部观测数据gi（x）＝u（x，Ti）∈H2（Ωi）∩H1（Ωi），i＝1，2，3，x∈Ωi，且T2－T1≠T3－T2，可以唯一的决定初值u0（x）与源项f（x）。

证明利用特征函数展开法，同理有

在辅助问题（5）中，取初值v（x，0）＝v0，2（x），则问题的解：

比较知，对任意的x∈Ω0，有v2（x，T2）＝g2（x）－g3（x）。从而知g2（x）－g3（x）在Ω0内解析，由解析延拓有

分析知，若g1（x）＝g2（x）＝g3（x）＝0，x∈Ωi，则有

2 反演算法

定理得证。

利用叠加原理，问题（1）可以分解为下面2个子问题：

显然有u（x，t）＝u1（x，t）＋u2（x，t）。定义子问题（11）与（12）的解算子为K1，K2，即：u1（x，t）＝K1［u0］（x，t），u2（x，t）＝K2［f］（x，t）。

显然有

采取有限元插值逼近技术考虑同时反演问题的反演算法，首先对空间求解域Ω进行剖分，d＝1时，取步长为h进行等距剖分，d＝2时，对Ω进行正则三角形分割，设分割所得域为Th，对应的内部节点集为。定义Vh为在剖分域Th上分片连续的有限元函数空间，即

考虑到与齐次边界的相容性，有u0｜∂Ω ＝f｜∂Ω ＝0。利用有限元插值，初值u0（x）和源项f（x）可以近似地表示为ψi（x）为线性有限元基函数，定义为：，其中u0，i＝u0（pi），fi＝f（pi），

因此，同时反演初值u0（x）与源项f（x）的问题近似转化为求2（N＋1）维实向量F＝［u0，0，…，u0，N，f0，…，fN］T的问题。

基于叠加原理，式（13）可以近似为：

在子问题（11）和子问题（12）中分别令u0（x）＝ψi（x），f（x）＝ψi（x），i＝0，1，…，N，利用有限元并行求解，得到K1［ψi］（x，Tk），K2［ψi］（x，Tk），i＝0，1，…，N，k＝1，2，3在区间Ωk上的数值解行向量，分别记为记gk分为gk（x），k＝1，2，3在Ωk内对应节点处的离散行向量。记应的离散方程组：则得到近似方程（14）对

你5岁时开始学象棋,还记得2015年参加南京市“金陵杯”象棋比赛吗？那次高手如云，且你年龄上也不占优势，最痛苦的是第一局你竟然输了。你有点失落，爸爸跟你说：“朗朗没事，只要下出自己应有的水平就行了！坚持就是胜利。”听了爸爸的话，你卸下包袱，过五关，斩六将，一路厮杀，超常发挥，结果获得了第二名的好成绩。站在领奖台上，你无比感慨,也记住了爸爸的话：坚持就是胜利！

考虑到反问题的不适定性，计算时采取下面Tikhonov正则化方法求解方程组（16），即

正则化参数α采用Morozov偏差准则来选取，即取正则化参数α满足其中τ为稍大于3的正常数。

综上所述，可以归结同时反演问题的反演算法，如算法1所示。

算法1反演算法

步骤1给定不同观测时刻的观测数据），k＝1，2，3，x∈Ω0，得到Gδ；

步骤2并行计算2N＋2个定解问题，得到向量组，＝0，1，…，N，k＝1，2，3，进而得到系数矩阵；

步骤3选取初始正则化参数α0及常数r∈（0，1），利用几何级数下降法αk＝选取满足偏差准则的后验正则化参数α*；

步骤4将后验正则化参数α*代入离散正则化方程组（17），求得正则化解向量，进而求得初值与源项的正则化解。

3 数值实验

3.1 实验装配

数值计算只考虑d＝1，2的情形。d＝1时，＝［0，1］，d＝2时时等距剖分为100个区间单元，d＝2时三角一致剖分为440个三角单元。观察数据是精确的数据（通过解析解或利用精确初值与源项通过数值求解正问题获得），ξi为在［－1，1］上服从均匀分布的随机变量。离散观测矩阵利用时间方向向后有限差分、空间方向有限元离散格式进行计算，其中时间取等距步长；当正问题不具有精确解时，观测数据通过采取时间方向向后有限差分、空间方向有限元离散格式求解正问题的途径来得到，其中时间离散步长当d＝1时，Ω0分别取定为以下3种情形：；当d＝2时，Ω0分别取定为以下2种情形：④

3.2 数值算例

例1d＝1，精确初值与源项分别取u0（x）＝πsin（πx）＋0.1sin（2πx），f（x）＝π2sin（πx），定解问题（1）有精确解u（x，t）＝0.1e－4π2tsin（2πx）＋（1＋（π－1）e－π2t）sin（πx）。

例2d＝2，设精确初值与源项分别取，定解问题（1）不存在精确解。

例1与例2的反演结果见表1。

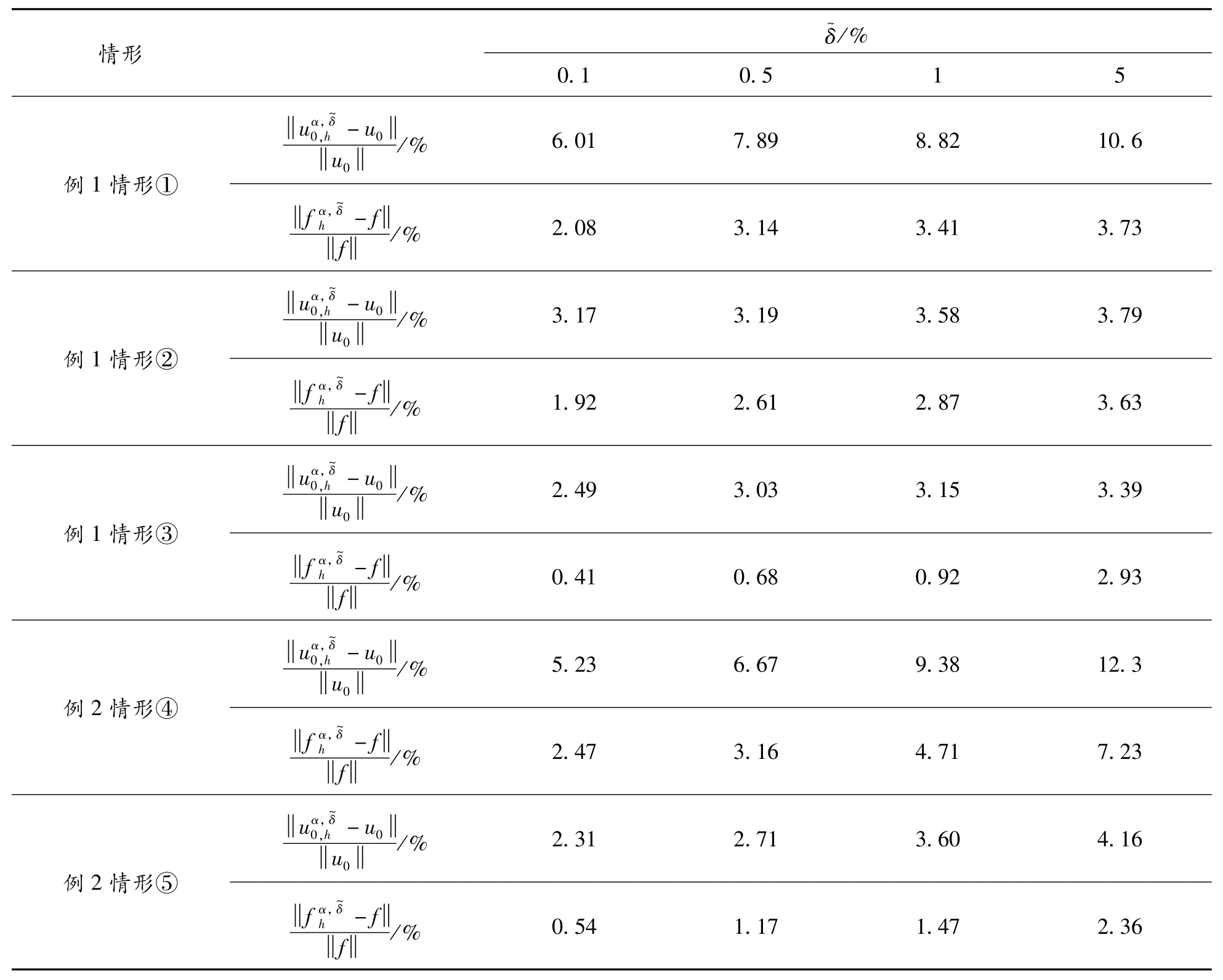
表1 不同观测噪声水平下反演解的相对误差

从表1及图1—图4计算结果可以看出，反演解随着噪声水平的逐渐减小越来越逼近精确解，显示算法具有良好的稳定性与收敛性，且从表1可以看出，观测区域较大时反演的结果整体比观测区域较小时反演的结果要好，导致的原因是在相同数量的观测数据下，大观测区域下观测数据反馈的信息比小观测区域下观测数据反馈的信息更全面，同样从表1可观察出源项反演的效果比初值反演的效果整体稍好，这也符合抛物型方程源项反问题的不适定性弱于逆时反问题的不适定性这一事实。

图1 例1精确初值曲线（a）及情形③不同噪声水平下反演初值对应的误差曲线（b）

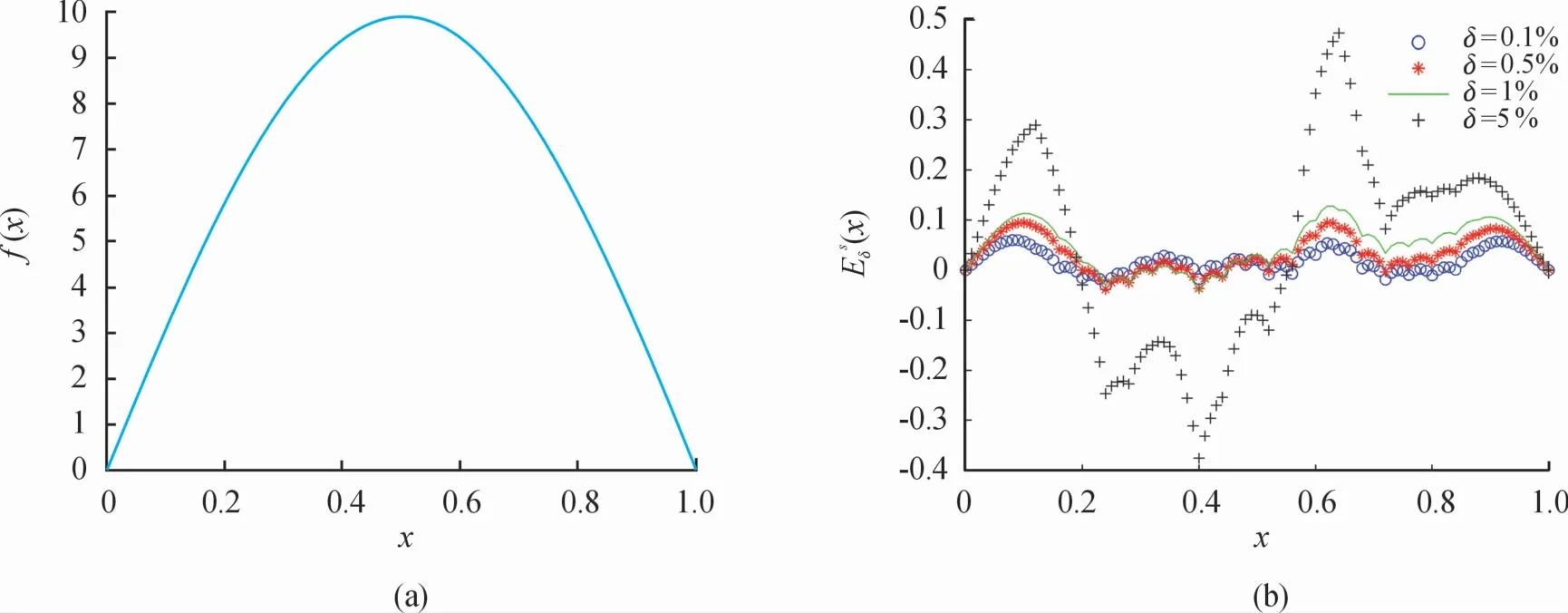
图2 例1精确源项曲线（a）及情形③不同噪声水平下反演源项对应的误差曲线（b）

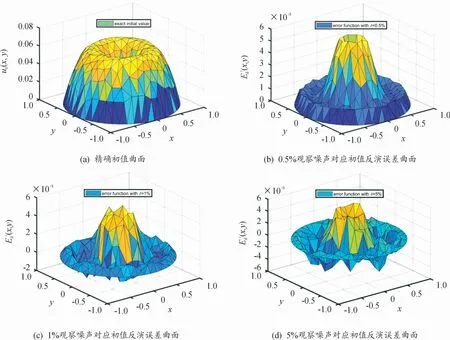
图3 例2精确初值曲面（a）及情形⑤时不同噪声水平下反演初值对应的误差曲面（b）、（c）、（d）

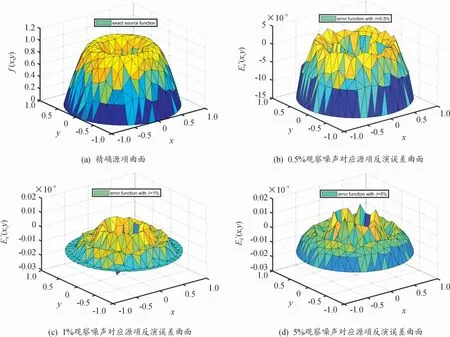
图4 例2精确源项曲面（a）及情形⑤时不同噪声水平下反演源项对应的误差曲面（b）、（c）、（d）

4 结论

基于特征函数展开法和抛物型方程解的解析延拓理论，建立了基于空间局部观测数据的一类抛物型方程源项与初值同时反演问题的唯一性理论，且借助于有限元插值方法及叠加原理，设计了易于并行的反演算法，并通过数值算例说明了反演算法的稳定性与收敛性。考虑的是基于局部观测数据的整数阶抛物型方程初值与源项同时反演问题，后续将考虑基于局部观测数据的分数阶抛物型方程初值与源项同时反演问题及其深度学习反演算法。