双膜量子点表面热流密度场测量技术

王一笑，张丹，涂茂萍，周文博，赵冰超

（1 西安交通大学能源与动力工程学院，陕西 西安 710049；2 华北水利水电大学能源与动力工程学院，河南 郑州 450045）

表面热流密度场测量在热力设施[1-2]、燃料电池[3-4]、旋转叶片[5-6]的传热性能评估等工业领域与相变传热过程[7-8]、高超音速风洞试验[9-10]等科学研究领域广泛存在。现有热流密度场测试技术按照测量原理的不同可以分为基于温度梯度测量的热电堆式热流计、基于热量平衡测量的水卡量热计以及基于半无限大体假设测量的薄膜热电偶热流计[11]。但是传感器体积大、布置复杂、系统惯性大等缺陷使得上述测量方式分辨率低、响应慢、成本高，而基于量子点测温的热流密度场测试技术成为突破上述瓶颈的有效途径之一。

量子点（quantum dots，QDs）是一种粒径约为10nm 的可发光半导体纳米材料，因具有发光稳定性强、光致荧光寿命长等优势被广泛应用于太阳能光热利用[12]、生物示踪[13]、图像增强[14]等领域。此外，量子点受激后会发出荧光，该光致荧光的峰值波长、峰值强度和半峰全宽等光谱参数均随量子点温度变化[15]，该现象被称为量子点光致荧光光谱（photoluminescence spectroscopy，PL）的温变效应。基于此效应，量子点亦可用于表面温度场的测量。闫海珍等[16]研究了CdSe/ZnS量子点的温变特性，结果指出在298～373K 范围内，光致荧光强度随温度的增大呈线性降低。陈中师等[17]设计了基于CdSe/ZnS核壳量子点薄膜光致荧光光谱温变特性的温度传感器，并得出在303～433K 温度范围内，随着温度的升高，CdSe/ZnS 核壳量子点的光致荧光光谱的自参考峰值强度线性减小，峰值波长线性增大。耿琰等[18]用发射波长分别为540nm和610nm的两种CdSe/ZnS 量子点制成双粒度的反射式荧光温度传感器，证明量子点的峰值波长可以作为温度测量时的参考量，平均灵敏度能够达到0.55nm/K。严金华等[19]利用PbSe 量子点开发了温度传感器，其灵敏度可达0.67nm/K。闫柯等[20]根据CdTe 量子点峰值波长的温变效应测量了轴承内圈温度，并与热电偶测量结果进行了比较，其绝对误差小于1K。本文作者课题组[21-23]利用量子点的温变效应设计了兼具加热与测温功能的试片，研究了固着液滴蒸发过程中底层温度场的演变。

可以看出，现有研究主要围绕温度场的测量展开，而根据量子点光致荧光光谱温变效应实现表面热流密度场的测量未见报道。于是，本研究提出在垂直热流方向上设置双层平行量子点薄膜，同时测量温度场，根据Fourier 导热定律计算得到热流密度场。据此设计了热流密度场测量试片及相应的实验系统，对测量试片进行了标定，分析了其反演结果的可靠性，并对测量效果开展了评价。

1 实验系统

1.1 量子点

选取图1所示的两种水溶性CdTe/CdS/ZnS量子点。该量子点均为图2所示核壳型结构。图3对比了两种量子点的吸收和光致荧光光谱，可以看出：①该量子点材料的吸收波段宽，最佳吸收波段为≤400nm的紫外光波段；②两种量子点材料的光致荧光光谱峰值波长分别为600nm和680nm。因此，实验中选择紫外光源激发，量子点发射出红色与橙色的光致荧光如图1(b)所示。

图1 CdTe/CdS/ZnS量子点溶液实物图

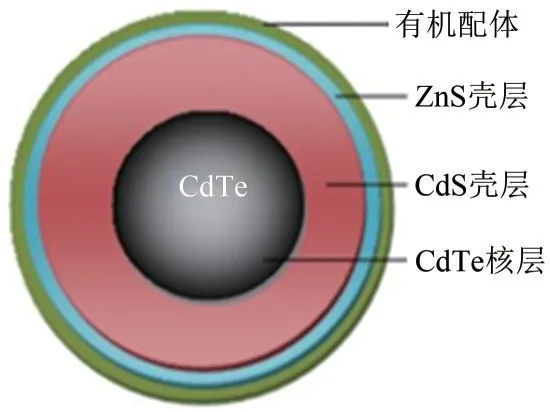
图2 水溶性CdTe/CdS/ZnS量子点结构

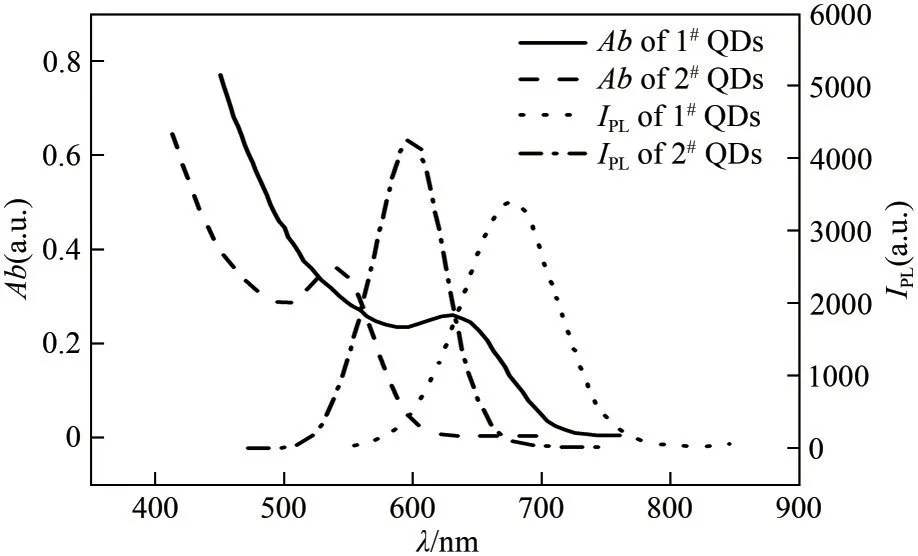
图3 CdTe/CdS/ZnS量子点的吸收和光致荧光光谱图

1.2 测量试片的结构

为实现利用量子点测量表面热流密度场，本研究设计了双膜量子点试片如图4所示。该试片为多片层结构，从下到上依次如下。

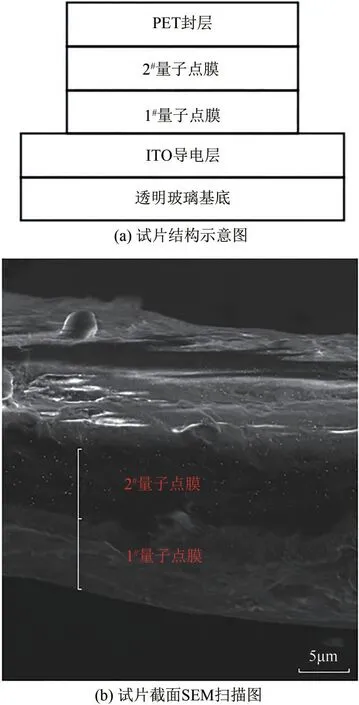
图4 双膜量子点试片结构图

（1）透明玻璃基底。该基底为试片提供强度支撑，同时满足激发光与光致荧光的透射。

（2）ITO（indium tin oxide，即氧化铟锡）导电层。该层通电后可实现试片的表面加热，用于后续实验中固着液滴的加热。

（3）1号量子点膜。其主要功能是测量所在位置的温度场。

（4）2号量子点膜。其主要功能是测量所在位置的温度场。

（5）PET封层。其主要功能是遮光。避免环境光对量子点的光致荧光的测量造成干扰。

1.3 热流密度场测试系统

热流密度场测试系统如图5所示。该系统包括光路测量系统和加热系统。光路测量系统主要包括双膜量子点试片、1#和2#两台CCD（charge coupled device）相机以及紫外（ultraviolet，UV）光源。其中，1#和2#CCD 相机分别在镜头前装有与1#和2#量子点光致荧光谱段对应的带通滤光片，其作用是使1#和2#量子点的光致荧光能分别透过该滤光片后被对应编号的CCD 相机采集。加热系统主要包括稳压电源、PID（proportional integral derivative）温度控制器、电热铜柱、铜电极等。系统部件参数见表1。该实验系统设计有标定、测量两种工作模式。温度控制器与电热铜柱用于标定模式下试片的标定；铜电极用于测量模式下为试片ITO层供电。此外，实验系统还包括数据采集系统和图像处理系统。

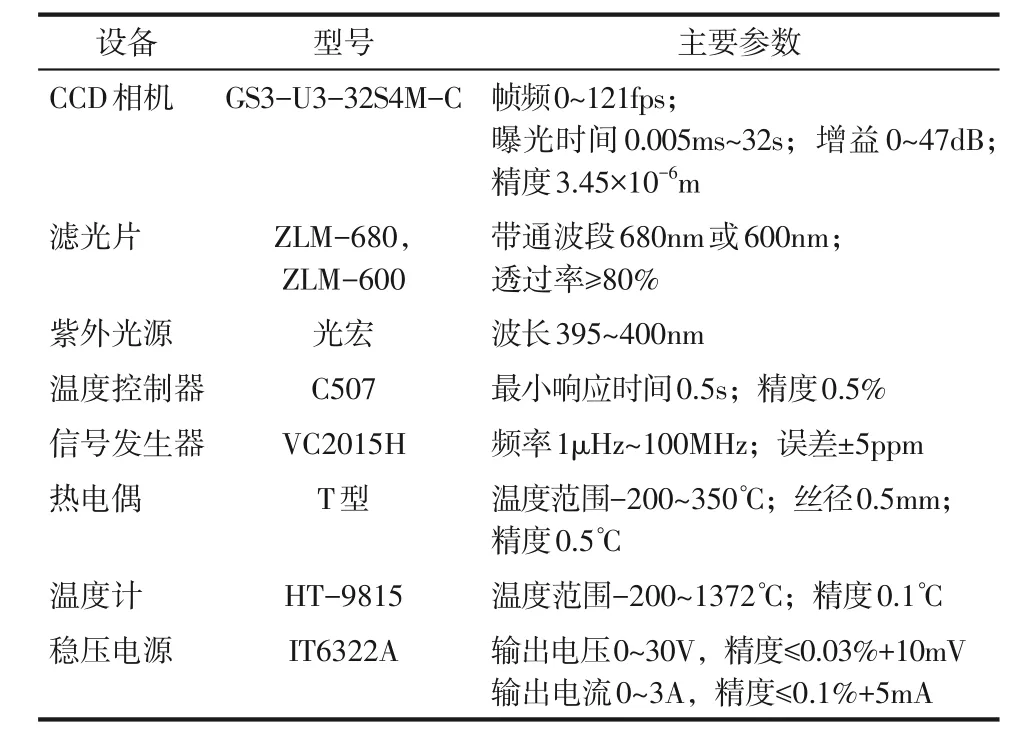
表1 系统部件参数

图5 热流密度场测试系统

本系统实验流程主要如下。

（1）标定。本研究采用稳态导热标定的方法对双膜量子点试片进行温度场标定，温度场标定实验系统如图5(a)所示。通过PID 温度控制器控制电热铜柱加热试片，在试片表面制造不同温度的均匀温度场，待1#和2#量子点膜之间达到热平衡后，使用两台CCD 相机分别拍摄并记录两层量子点膜的光致荧光强度场，建立两组图片中每个像素点光致荧光强度与温度的映射关系。

（2）测量。本研究选取固着液滴蒸发过程中底层温度场为测量对象，测量实验系统如图5(b)所示。将试片中的ITO导电层与外接稳压电源的铜电极相连，给ITO层通电后加热试片表面。然后将液滴滴加至试片表面，在液滴受热蒸发的同时，使用1#和2#两台CCD相机实时采集两层量子点膜的光致荧光强度场。

（3）反演。根据表面温度场的标定实验结果，将测量得到的1#和2#两层量子点膜的光致荧光强度场反演为对应的表面温度场。在此基础上，根据Fourier 导热定律进一步计算出垂直试片表面方向上的热流密度场。

2 实验结果分析

2.1 温度场标定

温度场标定的目的是获取图片中的每个像素点光强与温度的对应关系。为了定性展示该标定结果，选取试片有效测量区域如图6(a)所示，将该区域划分为NE、SE、NW、SW、C 这5 个分区，1#和2#量子点膜在每个区域内的平均光致荧光强度随温度的变化如图6(b)和(c)所示。可以看出，在本研究实验范围内，1#和2#量子点膜的平均光致荧光强度随温度的升高呈现线性下降趋势。

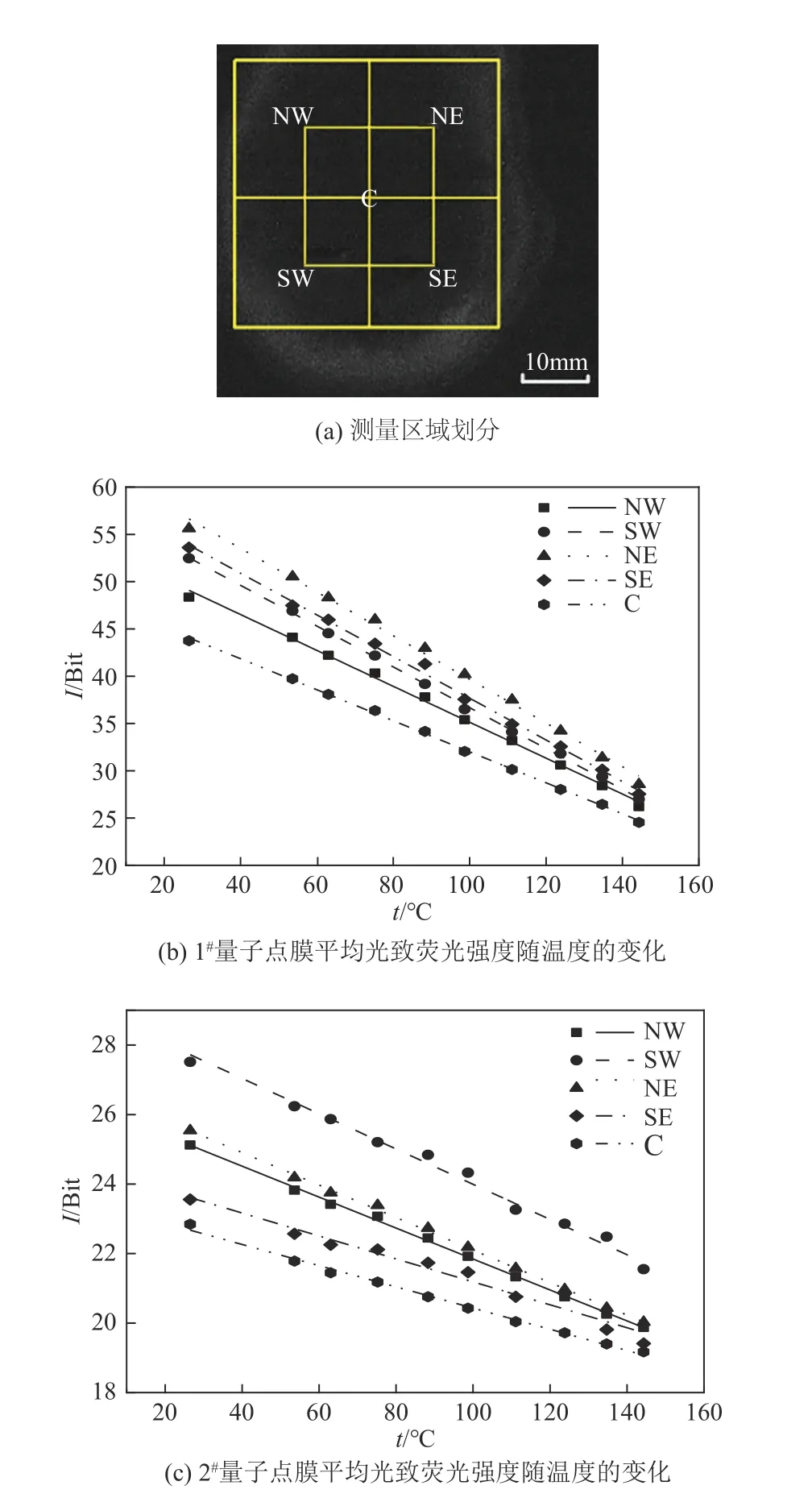
图6 试片温度标定结果

基于上述实验结果，通过最小二乘法可以建立温度场（t）与光致荧光强度场（I）的映射关系，如式(1)所示。以标定图片中10×10 像素区域为例，选区如图7(a)所示，对该区域内像素点依次编号如图7(b)所示，对每个像素点进行标定后得到的标定矩阵如图7(c)和(d)所示。

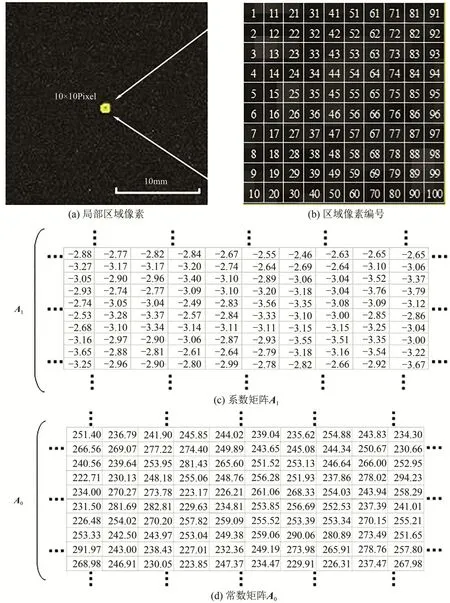
图7 像素点标定矩阵示意图

2.2 反演结果可靠性分析

根据得到的像素点标定矩阵，可以实现对标定过程中试片表面温度场的反演。如图8所示，反演结果能还原标定过程中试片表面的均匀温度场，图中标尺的不同颜色表示不同温度，颜色越蓝表示温度越低，颜色越红表示温度越高。

图8 标定过程中试片表面温度场反演结果

现对上述温度场反演结果的可靠性展开分析，本研究采用反演误差和不确定度作为评价温度场反演结果可靠性的参数。反演误差等于标定点上的反演温度与标定温度的绝对误差。测量区域内，平均反演精度如式(2)。

图9展示了全场平均反演绝对误差随标定温度的变化。根据图9可以看出：试片的温度绝对不确定度随标定温度升高没有明显变化规律；在测试温度范围内，反演的绝对误差为0.003～4.055K。

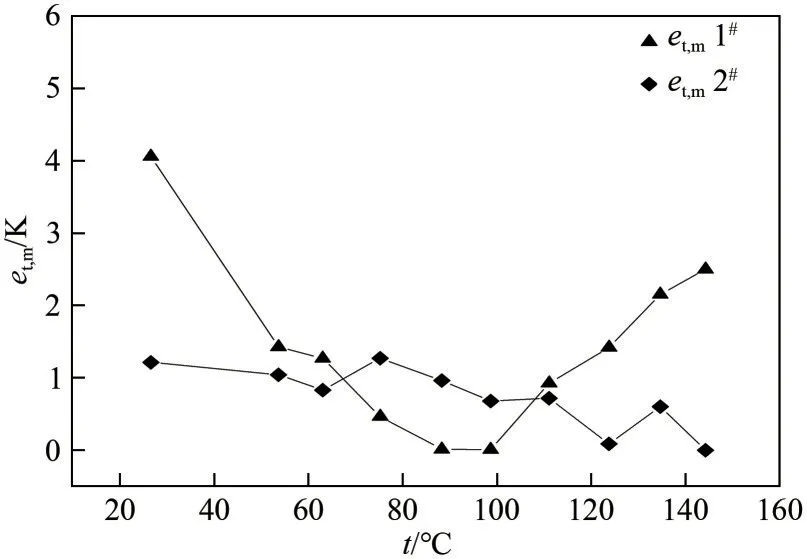
图9 温度场的反演误差

不确定度为被测量值不能被肯定的程度，是评价测量结果可靠性的重要参数。像素点的每个标定温度都有一个与之对应的整数型光强值，如图10所示，对应关系呈阶梯型，因此可以将各像素点的温度值与光强值刻度化。在本测量方法中光强值的最小刻度为1Bit，绝对不确定度为0.5Bit，通过比值计算，可得温度值的最小刻度及绝对不确定度。本研究测温方法是针对温度的场测量，由于每个像素点的温度-光强映射关系都不相同，导致不同像素点的温度绝对不确定度存在差异，故取其中的最大值作为评价测量结果可靠性的参数，如式(3)所示。

图10 不确定度计算方法示意图

现对试片测量区域内的温度不确定度进行计算，结果如图11 所示。结果表明：试片的温度绝对不确定度随标定温度升高没有明显变化规律；在测试温度范围内，试片的温度绝对不确定度为1.559～4.967K。

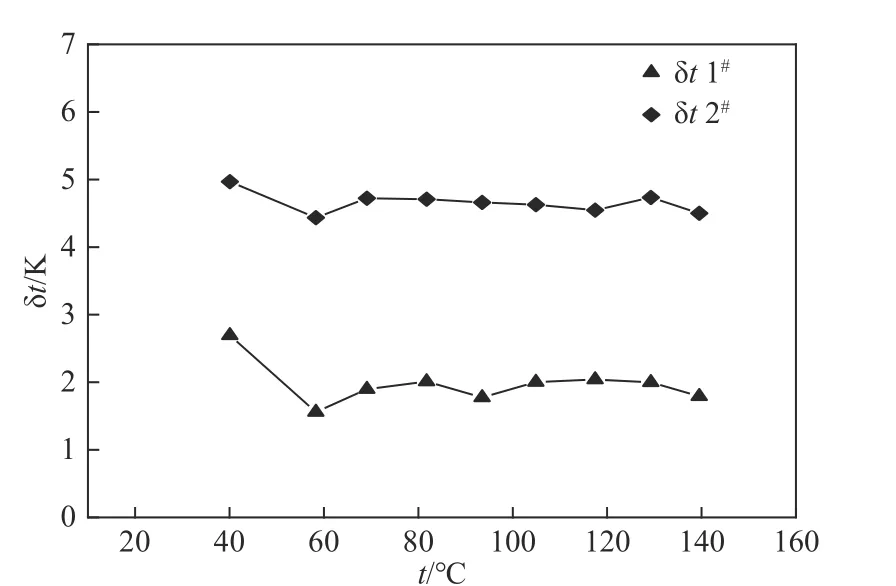
图11 不确定度测试结果

2.3 热流密度场测量效果分析

在温度场反演的基础上，可以根据式（4）计算出垂直方向上的热流密度场（q）。

通过稳压电源给试片中的ITO层施加30V电压，使试片表面充分加热，然后将室温下的纯水液滴滴加至试片表面，在液滴受热蒸发的同时实现对液滴底层热流密度场的测量，其测量反演结果如图12所示。

图12 液滴蒸发过程中底部热流密度场反演结果

根据以上反演结果，得到10s内纯水液滴受热蒸发过程中底层平均热流密度约为3.4×104W/m2。根据Moffat[24]所提出的Constant Odds Combination 方法，对本研究测量热流密度的不确定度进行分析。对于实验中可能涉及到大量的参数xi，通常将结果R写成式(5)形式，则R的不确定度计算式如式(6)所示，计算所得热流密度的不确定度为0.14。

现从空间分辨率和响应时间两个维度对本研究的测量效果进行分析。空间分辨率是指图像上能够区分的最小单元的尺寸，是评价传感器细节分辨性能的重要标准。考虑到底部相机与试片并非绝对垂直以及拍摄时相机的镜头畸变，单位像素在x、y方向上的空间分辨率可能不同。因此定义试片的空间分辨率为式(7)。

现对试片测量区域内的空间分辨率进行计算，如图13所示，被选中区域的图幅大小为530×510Pixel，实际大小为20.5mm×19.5mm，计算可得x轴和y轴方向的空间分辨率Zx和Zy分别为38.68μm/Pixel 和38.24μm/Pixel，结果表明本测量方法的空间分辨率可达30μm级。

图13 空间分辨率计算示例图

响应时间是衡量测试技术快速性的重要指标。任意测试技术在输入信号变化后输出结果的过程均可视为迟延与惯性环节的串联。如图14 所示，单位负阶跃信号斜率最大处的切线与横坐标轴交点τ1与τ2之差即为时间常数[25]。本研究定义响应时间为：测量系统从检测到温度变化到输出温度值与真实温度值偏差在5%内的时间，如式(8)所示。

τ5%s=-Tln 0.05 ≈3Tc(8)

式中，Tc=τ2-τ1。

热测量传感器的响应时间测试通常可以采用投入法[26]，即先将传感器置于一平衡初始温度下，然后快速投入不同温度的介质，以产生一阶跃输入，同时连续记录传感器的输出，并根据其输出数据计算时间常数。用投入法产生的温度阶跃，既可以是正阶跃，也可以是负阶跃。本研究即采用投入法原理对试片的响应时间进行测试，先将试片表面加热至较高的平衡温度，再向试片表面滴加纯水液滴。当温度为室温的纯水液滴接触高温试片时，接触面温度会迅速降低，相当于给试片输入了温度负阶跃。如图15所示，(a)为液滴落于试片表面过程图，可以看出液滴从开始下滴到完全落于试片表面耗时0.7s。这0.7s 内两层量子点膜对应的温度场变化分别如图15(b)和(c)所示，可以看出在这0.7s 内两层量子点膜的温度场变化并不明显，这是由于液滴未完全滴落以及试片本身的延迟响应所导致的。待液滴已完全滴落且被加热后，以此时两层量子点膜的温度场反演结果作为参考，确定液滴下落后的所在区域，在其中划分出编号1～5的5块分区，如图15(d)和(e)所示。分别对两层量子点膜上述分区位置内像素点的反演温度取均值，然后得出各分区平均温度随时间的变化关系，如图15(f)和(g)所示，进一步根据式(8)计算出该试片两层量子点膜的温度响应时间分别为3.42～4.32s和4.20～5.28s。结果表明本测量方法的响应时间为秒级。

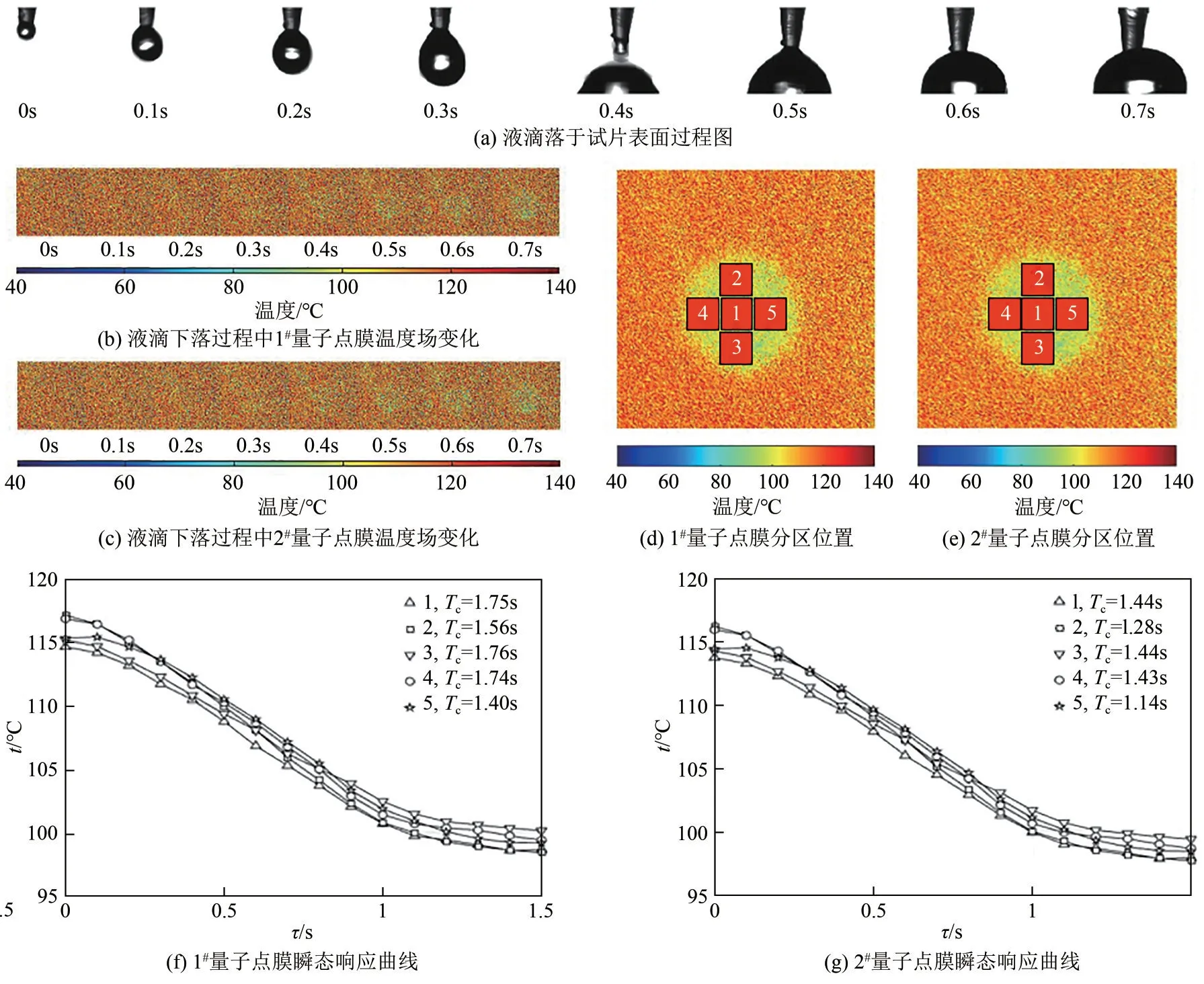
图15 响应时间处理结果

3 结论

本研究基于量子点光致荧光光谱的温变效应，开展了量子点表面热流密度场测量的实验研究，主要结论如下。

（1）为利用量子点光致荧光光谱的温变效应实现表面热流密度场的测量，本研究设计并制作了双膜量子点试片，结构从下到上依次为透明玻璃基底、ITO 导电层、两层量子点膜、PET 封层。并搭建了量子点热流密度场测量实验系统，其中主要包括光路测量系统和加热系统，可实现对试片的标定以及表面热流密度场的测量。

（2）对双膜量子点试片的温度场标定实验结果表明，在本研究实验范围内，量子点膜的平均光致荧光强度随温度的升高呈现线性下降趋势。反演结果表明在本研究实验范围内，温度场反演误差为0.003～4.055K，不确定度为1.559～4.967K，验证了本研究测量方法的可靠性。

（3）在温度场反演的基础上，根据Fourier 导热定律对蒸发过程中液滴底层热流密度场进行了反演，测得在本研究实验条件下10s内液滴受热蒸发过程中底层平均热流密度约为3.4×104W/m2。根据Moffat提出的Constant Odds Combination方法计算所得热流密度的不确定度为0.14。针对热流密度场反演结果的空间分辨率和响应时间进行了分析，结果表明本研究测量方法的空间分辨率可达30μm 级，响应时间为秒级，实现了对表面热流密度场的高分辨率、低延迟测量。

本研究可为集成式量子点热流密度传感器的设计和制作提供参考。基于本研究测量方法分辨率高、延迟低的优势，在某些传统测量方法难以开展的测试环境中，如针对高速旋转叶片、高超音速飞行器表面、微纳米元件等对象的传热性能测试，本研究拥有广阔的应用空间。

符号说明

A1，A0——分别为对像素点进行温度场标定后得到的系数矩阵和常数矩阵

Ab——吸收光谱强度

et,m——反演温度绝对误差，K

I——平均光致荧光强度，Bit

I——光致荧光强度场，Bit

Iclb——试片光致荧光强度场，Bit

Iclb,i,Iclb,i-1——分别为试片光致荧光强度场中变量，Bit

IPL——光致荧光光谱强度

k——热导率，W/(m·K)

q——热流密度场，W/m2

Tc——时间常数，s

t——温度，℃

t——温度场，℃

t1,t2——分别为两层量子点膜各自对应的温度场，℃

tclb——标定温度，K

tclb——标定温度场，K

tclb,i,tclb,i-1——分别为标定温度场中变量，K

Δx——厚度，m

ΔZr——实际距离，m

ΔZp——像素距离，Pixel

δt——单位光强值下温度绝对不确定度，K

λ——光谱波长，nm

τs——响应时间，s

τ1,τ2——分别为单位负阶跃信号斜率最大处切线与时间横轴的两个交点，s

下角标

max —— 最大值

x——x轴方向

y——y轴方向