西南小流域洪峰流量估算
李宁,张志兰,符素华,于秀娟,黄嵩
(1.北京师范大学地理科学学部,北京 100875;2.重庆市水土保持监测总站,重庆 401147)
洪峰流量可以表征径流搬运泥沙的能力[1],是修正土壤流失方程MUSLE[2]的重要参数。同时洪峰流量也是流域内建设堤坝、桥涵、水库等水利工程设施的重要参考因子。在全球变暖背景下,洪涝灾害、水土流失等问题日益加剧[3-9],分析水土流失影响因子,评估水土流失、洪涝灾害,提供预警显得尤为重要,洪峰流量是广泛应用水土评估模型SWAT 模型[10]的重要参数,是评估洪涝灾害不可缺少的重要参量,准确预测洪峰流量不仅是为科学决策提供可靠的数据支持,更是保护人民生命财产安全的需要。
计算洪峰流量的方法很多,如推理公式法、经验公式法、水文模型法等[11-14]。推理公式是基于暴雨形成洪水的基本原理推求设计洪水的方法,英、美国家称之为合理化公式[14],严格按照理论建立公式计算比较复杂,不适于实践应用推广。经验公式法[12]是通过数理统计得出的洪峰流量与其他相关变量的函数表达式,因其简单实用,多用于生产实践。目前针对中、大尺度流域建立的洪峰流量方程较多,但是适用于小流域的洪峰流量方程却很少,数据精度和可靠性是在小流域内建立洪峰流量模型的难点。一是建模型对数据精度要求高,二是小流域水文资料缺失、可靠性差[11,14]。小流域是我国进行水土流失综合治理、设计水土保持措施的基本单元,小流域土壤侵蚀特征及其影响因素也是当今全球研究热点之一[15-18],因此建立小流域尺度上的洪峰流量经验公式具有重要实践应用价值和迫切的现实需要。
1851年,Chow[19]的文章中基于径流系数、降雨强度和流域面积提出了第一个预测洪峰流量的方程式;1868年O′Connell[20]建立了洪峰流量与流域面积的指数方程;1977年,Williams等[2]以径流为自变量,建立了洪峰流量与径流之间的公式;1984年,蔡冠雄等[21]以福建省为实例,选择流域平均时段雨深、时段长、流域面积3个因素建立了洪峰流量经验公式;2008年,Fu等[22]基于中国黄土高原山西、陕西和甘肃24个流域399 次降雨事件数据检验并改进了CREAMS模型在黄土高原上的洪峰流量方程,该方程的自变量有流域面积(A),径流深和降雨量(P),但是没有考虑雨强因子;2017年,Liu等[23]基于陕西省5个径流小区和5个小流域的数据验证了洪峰流量方程在小流域尺度的适用性,采用量纲分析法和回归分析方法建立了两个新方程,方程中考虑的影响因素包括径流深(R)、降雨量(P)、最大30 min雨强和坡度(S)。2022年Shi等[24]应用黄土高原45个流域1 720次降雨事件数据,引入降雨强度和土壤水分因子,基于CREAMS模型改进了洪峰流量公式。
目前,中国估算小流域洪峰流量的研究区域主要集中在北方,如北京市、陕西省、山西省、甘肃省等[25]研究较多,而用于中国南方地区计算洪峰流量的经验公式较少。因此本研究以重庆万州刘家沟小流域为例,综合考虑水文气象特征,研究降雨量、径流深对洪峰流量的影响,初步验证Fu等[22]所建洪峰流量方程在西南地区的适用性,并基于此建立适用于重庆小流域的洪峰流量方程,为重庆地区乃至中国西南地区相似流域计算洪峰流量、制定水土保持措施、设计防洪工程项目、评价土壤与水资源、预防和评估洪涝灾害风险等提供科学依据。
1 材料与方法
1.1 研究区域与数据
本研究收集了重庆万州刘家沟小流域2013—2021年9 a共215次降雨径流数据。研究小流域控制站位于三峡库区腹心的重庆市万州区天城镇万河村,出口处地理坐标为东经108°21′45″,北纬30°53′45″。流域面积1.64 km2,流域形状系数0.43,主河道长3.10 km,平均坡降20%,坡度为15°~25°的陡坡和坡度为25°~35°的急陡坡占比95%以上,最大设计流量18.9 m3/s。刘家沟流域属典型的亚热带湿润季风气候,多年平均降雨量1 201.5 mm,年内降雨分配不均,降雨事件集中在5—9月,年际变化较大;多年平均气温17.8℃,极端最高、最低气温分别为42.1,3.7℃;多年平均相对湿度82%;多年平均日照时数1 295.3 h;无霜期349 d。流域内土壤以黄壤和棕紫色砂壤土为主,平均土层厚度20 cm,流域平均输沙模数99.78 t/(km2·a),土壤侵蚀模数2 826 t/(km2·a),流域综合治理度42%。流域内耕地占比约50%,园地和林地各占20%左右,还有少量牧草地及其他用地。天然植被以松、杉、柏等为主,主要分布在流域上游,林草覆盖率达到70%。人工植被以经果林为主,主要有油桐、桑树、柑桔、梨、板栗、杜仲等(图1)。
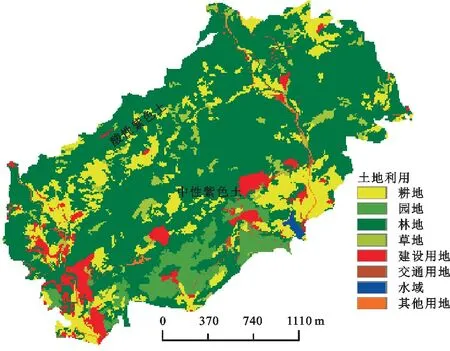
图1 刘家沟小流域土地利用类型Fig.1 Land use types of Liujiagou small watershed
1.2 研究方法
2008年,Fu等[22]基于中国黄土高原24个流域399次降雨事件检验并改进了CREAMS模型,以流域面积、径流深和降雨量为自变量,采用非线性回归的方法,建立了适用于中国黄土高原的洪峰流量方程。本文将使用研究区降雨径流数据探索公式(1)在研究区预测洪峰流量的可行性。
式中:Qp为洪峰流量(m3/s);A为流域面积(km2);R为径流深(mm);P为降雨量(mm)。
本研究以重庆万州刘家沟小流域为例,基于2013—2021年215次降雨事件,在SPSS 24.0软件中对洪峰流量、降雨量、平均雨强、最大30 min雨强、径流深、径流系数进行皮尔逊相关分析,以此了解研究流域的径流与洪峰流量特点。其中,为了消除流域面积对洪峰流量的影响,本研究采用洪峰流量模数的概念,洪峰流量模数定义为洪峰流量与流域面积的比值。
本研究基于流域215次降雨事件,校准验证Fu等[22]建立的洪峰流量方程。首先将所有数据根据洪峰流量从大到小排列,按规律抽出1/5的数据作为第二组验证数据,包括43组数据,其余4/5包括172组数据为第一组用于模型参数率定。之后使用软件SPSS 24.0采用非线性回归的方法建立洪峰流量方程。本文将对比两个模型在研究区对洪峰流量预测的准确性。本文使用Nash等[26]提出的模型有效系数来评估预测数据和实测数据之间的拟合优度。定义为:
式中:Ef为模型有效系数;Qobs为实测数据;Qcal为预测值;为实测数据的平均值。Ef取值范围为-∞~1;当Ef为1时,表示拟合值与测量值一致,拟合效果非常好;当Ef为0时,表示平均测量值和预测值是等效的。当Ef为负值时,表明拟合效果非常差。
2 结果与分析
2.1 径流特点及影响因素
次降雨的径流深变化范围是0.10~161.74 mm(图2),径流持续时间较长,均大于990 min,最大达到了17 678 min。径流深集中分布在0.10~10.00 mm,累计频率为60.47%;有少部分降雨事件径流深达到120 mm 以上,一方面由于降雨量较大,另一方面是因为前期有降雨使土壤前期含水量较大。研究区降雨时间比较集中,土壤含水量从饱和降到不饱和需要时间较长,这就导致连续降雨时,时间靠后的降雨事件产流量大,径流深较大。径流系数范围是0.003~0.91(图2)。径流系数小于0.5的累计频率高达83%,其中在0.0~0.1分布最集中,累计频率为25%。径流系数普遍较小,说明研究区的降雨以入渗为主,少部分形成地上径流。图2中可以看出径流系数存在比较大的情况,有3次降雨径流系数大于0.8,分别是2013年11月23日径流系数为0.91,2017年10月2日径流系数为0.82,2017年10月16日径流系数为0.81。这几天降雨之前曾有过降雨事件,使得这几天土壤前期含水量较大,土壤接近饱和状态,导致雨水入渗量少,大部分降雨用于产流,因此这几场降雨径流系数较大。在0.01置信度水平下,径流深与最大30 min雨强(I30)和降雨量呈显著正相关,与平均雨强显著不相关(表1)。因此在研究区内,对径流深影响较大的因素是降雨量和I30,降雨量和I30越大,径流深越大,产流越多。径流深与降雨量相关系数更大,说明径流深受降雨量影响更大。径流系数与平均雨强和I30的相关系数,均未通过显著性检验,说明平均雨强和I30对径流系数没有明显影响。径流系数与降雨量的相关系数为0.364,二者呈显著正相关,这说明径流系数会随着降雨量增多而变大。在Fu等[22]研究的黄土高原丘陵沟壑区,径流系数与所有降雨特征值均呈显著正相关(p=0.01),其中降雨强度与径流系数的相关性更好,最大30 min雨强与径流系数相关系数最大,降雨量与径流系数的相关系数最小[27]。这与本研究区结果相反,本研究区的降雨量与径流系数相关系数最大,降雨强度对径流系数的影响反而更小。

表1 径流深、径流系数影响因素分析Table 1 Effect factor analysis of runoff depth and runoff coefficient
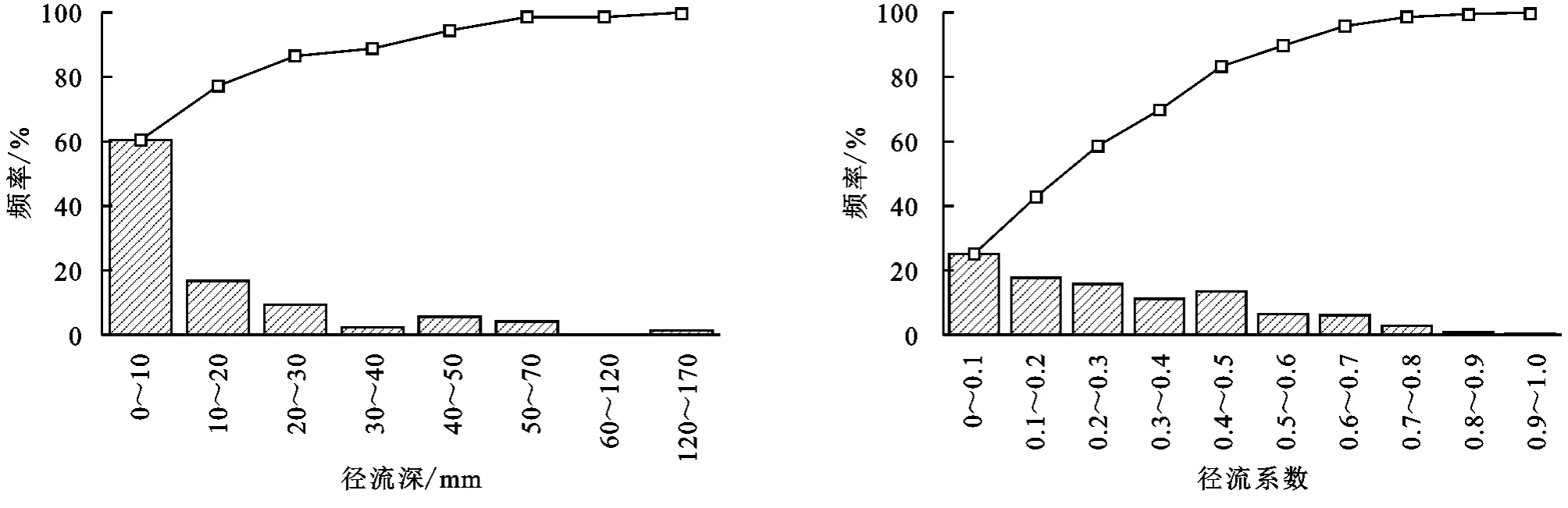
图2 径流深、径流系数频率Fig.2 Runoff depth and runoff coefficient frequency
2.2 洪峰流量特点及影响因素
研究区2013—2021年洪峰流量范围是0.001~11.010 m3/s,洪峰模数范围是0.000 6~6.71 m3/(s·km2)。流域内洪水以单峰和双峰为主,少数以多峰形式呈现。较高的洪峰流量多发生在6—9月份。洪峰流量集中在0.00~0.500 m3/s,分布占比67%。洪峰模数主要集中在0.00~0.50 m3/(s·km2),占比74%(图3)。在0.01置信度水平下,降雨参数中降雨量和I30与洪峰流量呈显著正相关,其中降雨量与洪峰流量的相关性更强,相关系数为0.684,而平均雨强与洪峰流量的相关系数在统计上不显著。径流参数中径流深和径流系数与洪峰流量的相关系数均表现显著正相关(表2)。随着最大30 min雨强、降雨量、径流深、径流系数几个因素变化,洪峰流量也会同方向变化,其中降雨量和径流深对洪峰流量的影响更大。Liu等[23]研究表明,黄土高原丘陵沟壑区的洪峰流量比本研究区要大得多,黄土高原的洪峰流量与径流深、降雨量和最大30 min降雨强度显著正相关,最大30 min雨强与洪峰流量的相关系数最大。本研究区与Fu等[22]研究的黄土高原相比,洪峰流量和径流深、降雨量的关系有相似性,均呈显著正相关;同时也有区别,在本研究区,降雨量与洪峰流量的相关性更强,而在黄土高原,最大30 min雨强与洪峰流量的相关性更强。这些相似点是本文将Fu等[22]所建立的洪峰流量模型应用于重庆地区的前提,不同点则可能引起两地区洪峰流量模型出现差异,为基于该模型建立新洪峰流量模型提供依据。

表2 洪峰流量影响因素分析Table 2 Effect factor analysis of peak flow rates
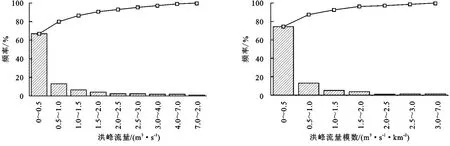
图3 洪峰流量、洪峰流量模数频率Fig.3 Peak flow rates and peak flow modulus frequency
2.3 模型校准与验证
图4是根据Fu等[22]公式(1)预测的洪峰流量与实际洪峰流量做出的对比图,点全部分布在1∶1比例线的上方,说明方程远远高估了洪峰流量,模型有效系数为-196.45,方程预测效果不好,因此,公式(1)不适用于重庆小流域洪峰流量的计算。但是,预测的洪峰流量与实际洪峰流量线性关系较为明显,这些结果表明,公式(1)中的变量是影响洪峰流量的重要参数,但该等式的系数或形式不适合预测重庆地区的洪峰流量。

图4 公式(1)预测洪峰流量与实际洪峰流量Fig.4 Measured versus predicted peak flow rates using equation(1)
首先保证方程(1)中自变量径流深(R)和降雨量(P)的指数形式不变,对洪峰流量Qp与Q'=A0.59R1.15A0.06P-0.72直接进行线性回归分析,结果得到Q'=A0.59R1.15A0.06P-0.72的系数为-2.27,通过显著性检验,说明因变量洪峰流量Qp与Q'之间存在线性关系。因此得到计算洪峰流量Qp的新方程:
虽然变异数显示因变量洪峰流量Qp与Q'之间存在显著的回归关系,但是模型的判定系数R2为0.061,说明能够被方程解释的数据部分占比较小,计算模型有效系数只有0.06,该模型解释效果不好,需要继续优化。
直接进行线性回归效果不理想,因此保持公式(1)的形式不变,使用非线性回归法重新拟合更优的指数参数。公式左右两边同时取底数为10的对数,根据公式(4)进行回归分析,得到方程(5),整理得到公式(6)。回归结果表示,A0.06·lgR系数a1为0.977,lgP的系数a2为0.3,系数均通过显著性检验。
变异数分析表明自变量与因变量之间存在显著的回归关系,模型判定系数R2=0.823,调整后R2=0.821,可知该模型解释效果较好。使用第一组数据模拟出的预测洪峰流量,与实际洪峰流量计算出的模型有效系数为0.51,使用第二组数据验证模型,计算模型有效系数为0.68,公式(6)模型有效系数相较于公式(3)有了明显提高。
在洪峰流量与其他因子的相关性分析中(表2),洪峰流量与I30显著相关,I30对洪峰流量影响较大,因此在模型中添加自变量I30。以洪峰流量为因变量,降雨量、径流深、I30作为自变量进行非线性回归,得到新方程:
模型判定系数R2为0.847,可知该模型解释效果较好。使用第一组数据模拟出洪峰流量,计算模型有效系数较高,为0.85。图5是根据结果做出的预测洪峰流量与实际洪峰流量散点图,点均匀紧凑地分布在1∶1比例线的两侧,说明预测洪峰流量与实际洪峰流量值十分接近,方程预测洪峰流量效果较好。

图5 公式(7)校准数据中预测洪峰流量与实际洪峰流量对比Fig.5 Measured versus formula(7)predicted-peak flow rates for the developmental data set
使用第二组数据验证模型,计算模型有效系数为0.82。图6是根据结果作出的预测洪峰流量与实际洪峰流量散点图,点均匀紧凑地分布在1∶1比例线的两侧,说明预测洪峰流量与实际洪峰流量值十分接近,再次验证公式(7)预测洪峰流量效果较好。
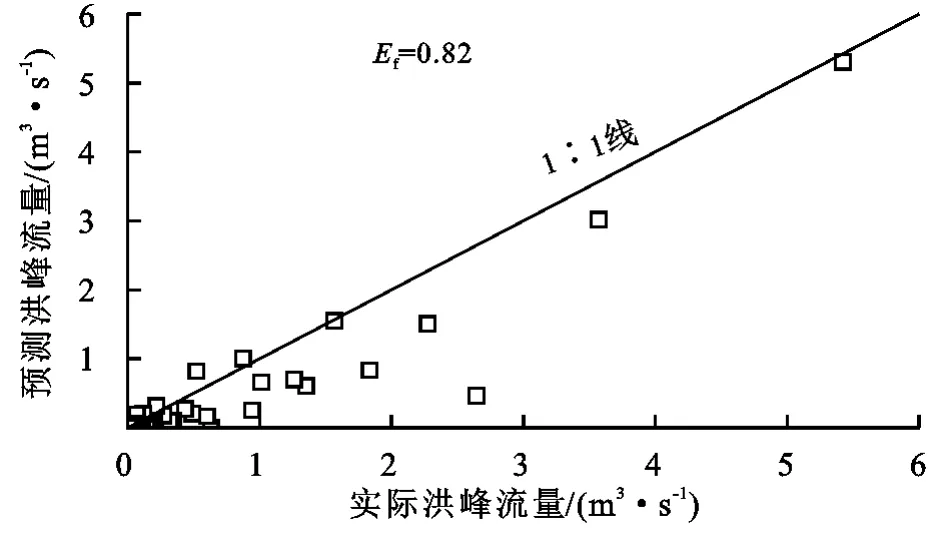
图6 公式(7)验证数据中预测洪峰流量与实际洪峰流量对比Fig.6 Measured versus formula(7)predicted-peak flow rates for the independent test data set
2.4 模型对比
基于Fu等[22]公式(1)调整参数后的公式(6)相较于公式(7)自变量里没有最大30 min雨强因子。其中图7和图8是根据公式(6)预测的洪峰流量与实际洪峰流量做出的对比图,可以明显看出,公式(6)高估了较小的洪峰流量,低估了较高的洪峰流量;公式(6)的模型有效系数分别为0.51,0.68。然而,从图5和图6可以看出式(7)预测的洪峰流量均与实际洪峰流量相近,模型有效系数分别为0.85,0.82,高于公式(6)的模型有效系数,公式(7)预测洪峰流量更为准确。

图7 公式(6)校准数据中预测洪峰流量与实际洪峰流量对比图Fig.7 Measured versus Formula(6)predicted-peak flow rates for the developmental data set
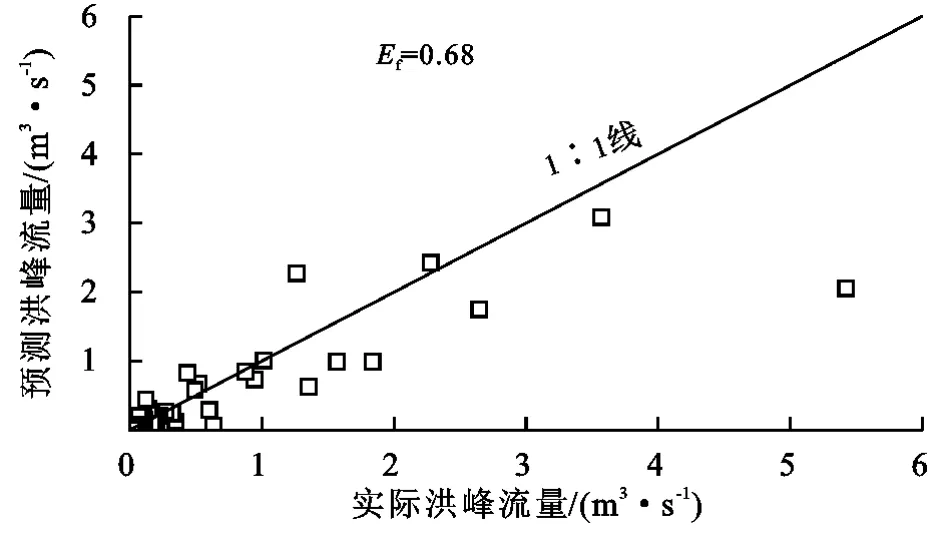
图8 公式(6)验证数据中预测洪峰流量与实际洪峰流量对比图Fig.8 Measured versus formula(6)predicted-peak flow rates for the independent test data set
公式(7)与Fu等[22]所建公式(1)相比有两点明显的改变,一是方程系数,公式(1)方程系数为6.69,公式(7)方程系数为0.006;二是公式(7)比公式(1)多考虑了最大30分钟雨强因子,本文研究区内洪峰流量与I30显著相关,在模型中加入I30使模型有效系数明显提高,这说明I30对于重地区的洪峰流量预测影响较大。本文研究区重庆位于中国湿润地区,Fu等[22]的研究区黄土高原位于半干旱、半湿润地区。对比两地区的洪峰流量,黄土高原普遍比重庆的洪峰流量大,因此本文新建方程系数较小合乎常理;黄土高原沟壑纵横,Fu等[22]所研究的区域80%以上坡度大于10°,土壤以黄土为主,本文研究区96%以上坡度大于15°,以壤土为主,地形起伏均较大;在降雨特征方面,黄土高原多为短期强降雨[27-28],而重庆地区的降雨持续时间长,雨强普遍较小;在产流特征方面,黄土高原通常为超渗产流,重庆地区多为蓄满产流,降雨量对于洪峰流量影响较大,而且重庆地区到了雨季,阴雨连绵不绝,长时间的降雨会使流域达到最大蓄水量,那么之后降雨便会几乎全部形成径流,洪峰流量也随之增大,降雨量和降雨时间对洪峰流量的形成都起到了重要作用,在方程中加入最大30 min雨强显著提高了模型有效系数。
3 结论
本文分析了重庆万州刘家沟小流域的径流与洪峰流量特点,并与黄土高原地区做了对比。在本研究范围内,径流深和降雨量、最大30 min雨强均呈显著正相关,降雨量对径流深和径流系数的影响最大。然而在黄土高原丘陵沟壑区,其降雨径流特征表现不同,最大30 min雨强与径流系数相关性更好,降雨量与径流系数的相关系数反而最小[27]。关于洪峰流量,本研究区的洪峰流量与降雨参数中降雨量和最大30 min雨强以及径流参数中径流深和径流系数有较好的相关关系,其中降雨量与洪峰流量的相关性更强。而在黄土高原区,却是最大30 min雨强与洪峰流量相关性更强。
本文使用重庆万州刘家沟小流域215次降雨事件的数据对Fu等[22]建立的洪峰流量方程进行校准,两者研究区地形特征相似,均为陡坡条件,但是降雨特征有较大差异,于是在新方程中引入最大30 min雨强作为新的自变量,建立了洪峰流量公式(7)。公式(7)自变量包括流域面积、降雨量、径流深和最大30 min雨强,该模型具有较高的模型有效系数,参数率定和模型验证的模型有效系数分别为0.85,0.82,能够较好地预测研究流域的洪峰流量。本文建立的公式是对现有的洪峰流量公式的补充,将有助于预测湿润地区相似流域条件下的洪峰流量,为水资源保护、水土保持研究、预防和评估洪涝灾害风险等提供帮助和参考。

