中国城市群财政科技投入绩效的时空演化研究

曾 鹏，魏 然，魏 旭

（广西民族大学a.民族学与社会学学院；b.经济学院；c.管理学院，南宁 530006）

0 引言

科技创新是实现中华民族伟大复兴的强大驱动力[1]。在我国的科技资源投入中，政府的财政科技投入是科技资源投入的重要来源，基于财政视角探究科技资源投入转化效率对我国科技发展具有长远意义。城市群作为城镇化的新型主体单元，在科技创新发展中承担着重要支撑作用，是科技创新的重要策源地[2]。探究和把握城市群财政科技投入绩效的时空演化格局有助于整体把握城市群科技发展现状，为制订城市群科技产业政策、推动科技产业高质量发展奠定理论基础。

财政科技投入绩效，为财政科技项目投入产出所取得的实际效果，是科技产业效率评价研究的一方面，着重研究财政配置资源的有效性[3]。当前关于科技产业投入绩效评价的研究较为丰富，国内较早可以追溯到袁嘉新（1992）[4]对测算科技进步的方法进行讨论；国外较早可以追溯到Frsund（1980）[5]对随机前沿生产函数及其与效率测度关系的分析。近年来，基于科技产业及绩效评价的研究方法，学者们较多使用DEA模型、SFA模型、StoNED模型、Tobit 模型、三阶段DEA 模型、DEA-Malmquist 指数模型等[6—8]。对于科技产业效率评价的研究而言，学者们较多集中于国别[9]、省域[10]和市域[11]等视角进行研究。当前以城市群为研究视域探究科技产业效率评价的学术研究较少，主要为单个城市群科技资源效率及绩效的评价研究，对中国城市群整体的科技产业效率评价研究较少[12]。

综上，本文建立三阶段DEA 模型静态评估城市群财政科技投入绩效；基于三阶段DEA 模型计算结果进行趋势面分析，探讨城市群财政科技投入绩效空间演化规律；引入Malmquist 指数，进一步研究城市群财政科技投入绩效在时间序列上的动态演化。

1 研究设计

1.1 研究范围

本文参照国务院、国家发展和改革委员会以及各省（直辖市、区）级政府批复印发的19 个城市群发展规划文件，确定中国的城市群分布状况，其中包含重点建设五大国家级城市群（长江三角洲、珠江三角洲、京津冀、长江中游、成渝），稳步建设八大区域级城市群（山东半岛、粤闽浙沿海①“十四五”规划纲要中，“海峡西岸城市群”的表述被“粤闽浙沿海城市群”所代替。、中原、关中平原、辽中南、哈长、北部湾、天山北坡），引导培育六大地区级城市群（滇中、黔中、晋中、兰西、呼包鄂榆、宁夏沿黄）的229 个城市。由于数据样本可能出现重叠，且部分城市数据缺失严重，因此将部分城市剔除，对剩余203个城市进行研究。

1.2 研究方法

1.2.1 三阶段DEA模型

本文采用三阶段DEA模型测算中国城市群的财政科技投入绩效。具体可分为如下三阶段：

第一阶段为传统DEA模型。通过使用传统DEA模型将中国城市群的203个城市看作基本决策单元DMU以测算财政科技投入绩效值，并进一步求得科技投入的松弛值，为第二阶段SFA回归估计奠定基础。由于现实科技投入生产中规模报酬是可变的，因此本文选取DEA-BBC 模型，并基于投入导向型测算决策单元的财政科技投入绩效。

其中，j=1,2,…,203 表示基本决策单元DMU，即城市群所辖城市；X和Y分别为科技投入和科技产出向量。θ为决策单元的有效值；ε为常量，表示非阿基米德无穷小；s-和s+表示科技投入松弛变量和科技产出松弛变量。若θ=1，s+=s-=0，则决策单元DEA有效，DMU财政科技投入绩效达到纯技术效率最佳和规模效率最佳。若θ=1，s+≠0，或s-≠0，则决策单元弱DEA有效。若θ=1，则决策单元非DEA有效，DMU财政科技投入绩效没有达到纯技术效率最佳和规模效率最佳。DEA-BBC模型的计算结果为综合技术效率（TE），可以通过纯技术效率（PTE）和规模效率（SE）对其进行分解，即TE=PTE*SE。

第二阶段为相似随机前沿模型。由于第一阶段DEA模型是选择投入导向型，因此仅对投入松弛变量进行SFA回归分解，分析第一阶段中的投入松弛变量与外生环境变量、随机误差项之间的关系，进而调整投入变量。首先构造类SFA回归函数：

SFA回归将所有决策单元调整到相同的外部环境中，消除环境因素和随机因素对效率测度的影响，得到能够直接反映管理水平的效率值，鉴于该模型使用较为成熟，不作详细展示。其具体调整公式如下：

第三阶段，将消除环境因素和随机误差因素的修正科技投入变量和原始科技产出变量导入DEA模型进行截面数据的逐年测算，进一步得到修正后的财政科技投入综合技术效率（TE）、纯技术效率（PTE）和规模效率（SE）。

1.2.2 DEA-Malmquist指数

三阶段DEA模型是对财政科技投入绩效进行静态分析，并不能具体反映全要素生产率随时间的变动趋势，Malmquist指数是一种用来衡量全要素生产率变化率的方法，因此本文选取Malmquist 指数对科技投入全要素生产率进行分析[13]。

设(Xt,Yt)和(Xt+1,Yt+1) 分别为t期和t+1 期的投入产出关系，生产率变化为由(Xt,Yt)向(Xt+1,Yt+1) 的变化。Dt(Xt,Yt)和Dt+1(Xt+1,Yt+1) 为规模报酬不变时的距离函数。基于t期和t+1期的全要素生产率指数M为：

若M＜1，则表明从t期至t+1 期，全要素生产率水平降低；若M＞1，则表明从t期至t+1 期，全要素生产率水平提高。对全要素生产率TFPch可进一步分解如下[14]：

其中，PEch为纯技术效率变化，TEch为技术变化，SEch为规模效率变化。

1.3 变量选取及预处理

本文基于三阶段DEA-Malmquist 模型测算中国城市群财政科技投入绩效，选取财政支出中科学技术支出和年末城镇科学研究、技术服务和地质勘查业从业人员作为科技投入变量，选取发明专利授权量、实用新型专利授权量、外观设计专利授权量和专利授权总量作为科技产出变量，并选取人均地区生产总值、第二产业产值占地区生产总值比重、财政支出中教育支出分别衡量经济水平、产业结构和教育支持等外部环境变量。

原始变量数据不能直接投入模型进行计算，需要对原始数据进行预处理使得数据模型计算更加精确合理。第一，由于各变量原始数据之间单位和数量级存在较大差异，为了简化计算，本文使用归一化对原始数据指标进行无量纲化处理，此时变量数据范围为0～1；第二，为了防止在SFA回归模型计算时出现系数过小的情况，对归一化后的数据范围扩充100倍，使得变量数据范围为0～100；第三，由于在DEA模型计算处理时变量不能出现零值，因此在每项变量数据后增加0.001对数据整体进行非负处理。最后，将经过三步数据处理后的变量投入DEA模型进行计算分析。

1.4 数据来源

本文用于中国城市群财政科技投入绩效计算的空间面板数据区间为2011—2021年，其中经济相关数据、科技产业相关数据均来自2012—2022年《中国城市统计年鉴》《中国科技统计年鉴》以及中国和各城市国民经济和社会发展统计公报；部分科技产业相关数据来自2012—2022年各省份统计年鉴；少数漏缺数据来自国家统计局官网及各省统计局官网；极个别数据缺失通过平滑处理进行补充。

2 城市群财政科技投入绩效的空间格局分析

2.1 三阶段DEA模型的结果分析

2.1.1 第一阶段传统DEA模型的结果分析

运用DEAP 2.1 软件测算中国城市群203 个城市2011—2021 年的综合技术效率（TE）、纯技术效率（PTE）、规模效率（SE）以及投入要素松弛变量，其中SE=TE/PTE。因受篇幅所限，本文仅将综合技术效率和纯技术效率结果作简单的描述性统计（见下页表1）。

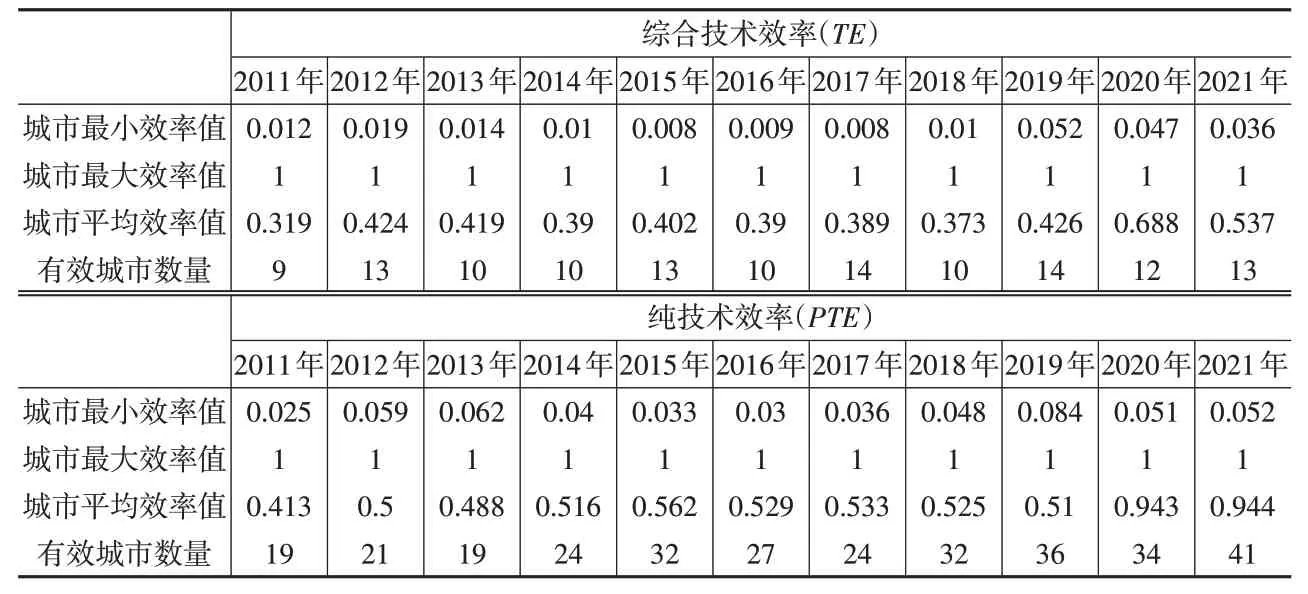
表1 城市群所辖城市财政科技投入绩效统计表（第一阶段）

由表1可知，在忽略外部环境和随机因素的影响下，中国城市群城市间财政科技投入综合技术效率和纯技术效率差异较大，历年TE的最小值和均值均远小于PTE。

通过对城市群203 个DMU（城市）2011—2021 年的财政科技投入综合技术效率（TE）和纯技术效率（PTE）进行加总平均得到19 个城市群各自的效率均值，并继而计算得出重点建设国家级、稳步建设区域级和引导培育地区级城市群以及城市群的总体效率均值并进行描述性统计分析（见表2）。

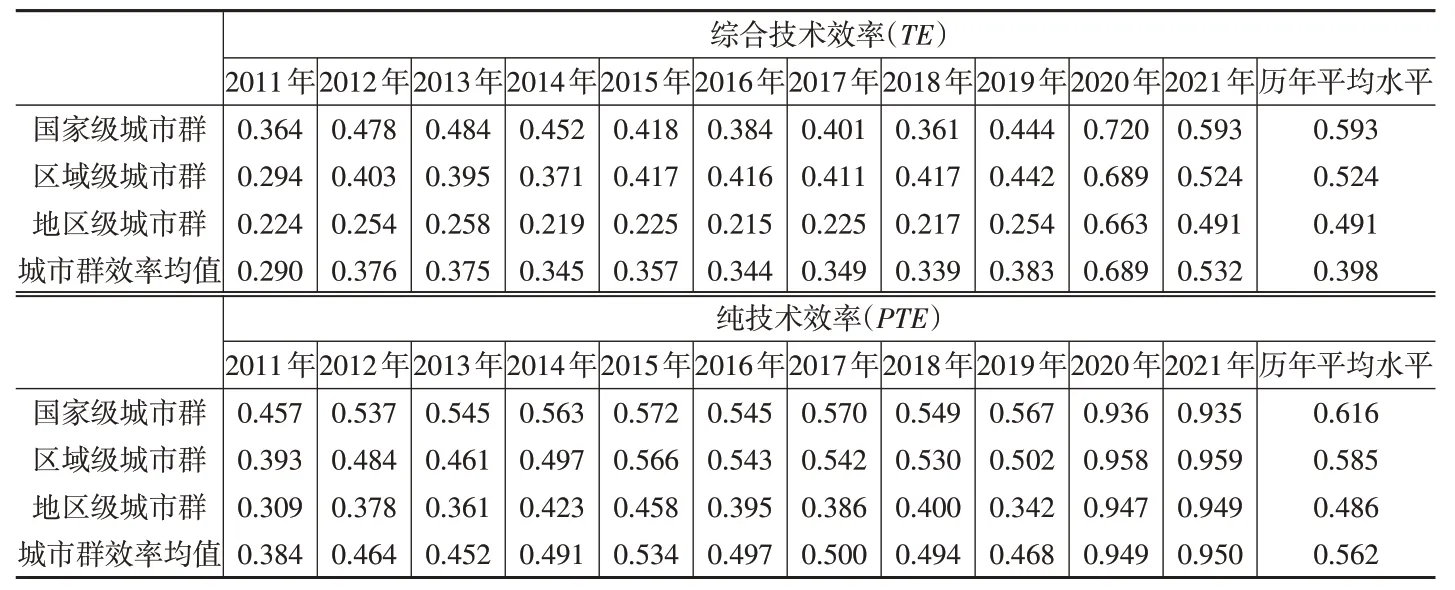
表2 城市群财政科技投入绩效演化

由表2可知，从财政科技投入综合技术效率（TE）整体水平来看，国家级城市群效率最高，区域级城市群次之，地区级城市群最末。从财政科技投入纯技术效率（PE）来看，同样，国家级城市群效率最高，区域级城市群次之，地区级城市群最末。

2.1.2 第二阶段SFA回归结果分析

将第一阶段DEA模型所求得的科学技术行业从业人员和科学技术支出的投入松弛变量作为被解释变量，以经济水平、产业结构和教育支持作为解释变量分析外部环境变量对投入松弛变量的影响，运用Frontier 4.1 软件建立SFA回归模型，结果如表3所示。

表3 第二阶段SFA回归结果

根据表3可知，第一阶段DEA财政科技投入绩效测算的两项投入松弛变量的单边误差似然比检验均通过显著性检验，拒绝原假设，表明SFA回归模型合理。且投入松弛变量的γ值均趋近于1，σ2、γ同样通过显著性检验，表明混合误差项中的管理无效率对投入松弛变量影响较大，而随机误差的影响较小[15]。

从经济水平、产业结构和教育支持各项外部环境变量来看，其估计系数均通过了显著性检验，说明环境因素对科技投入的松弛变量具有显著影响。由表3 可知，经济水平、教育支持和产业结构对投入松弛变量的估计系数为正，不利于财政科技投入绩效的提升。

为了消除外部环境变量和随机误差因素影响，需要对科技投入变量进行调整，重新进行财政科技投入绩效的测算，以增强结果的准确性、可信性。

2.1.3 第三阶段调整后的DEA模型实证结果分析

通过对2011—2021 年各科技投入变量进行调整，并利用DEAP 2.1 软件将其与原始产出变量合并，导入投入导向型DEA-BBC 模型进行逐年测算，得到剔除外部环境和随机误差因素的城市群财政科技投入绩效，即城市群财政科技投入综合技术效率（TE）、规模效率（SE）和纯技术效率（PTE），并将财政科技投入综合技术效率、纯技术效率作简单的描述性统计（见下页表4）。

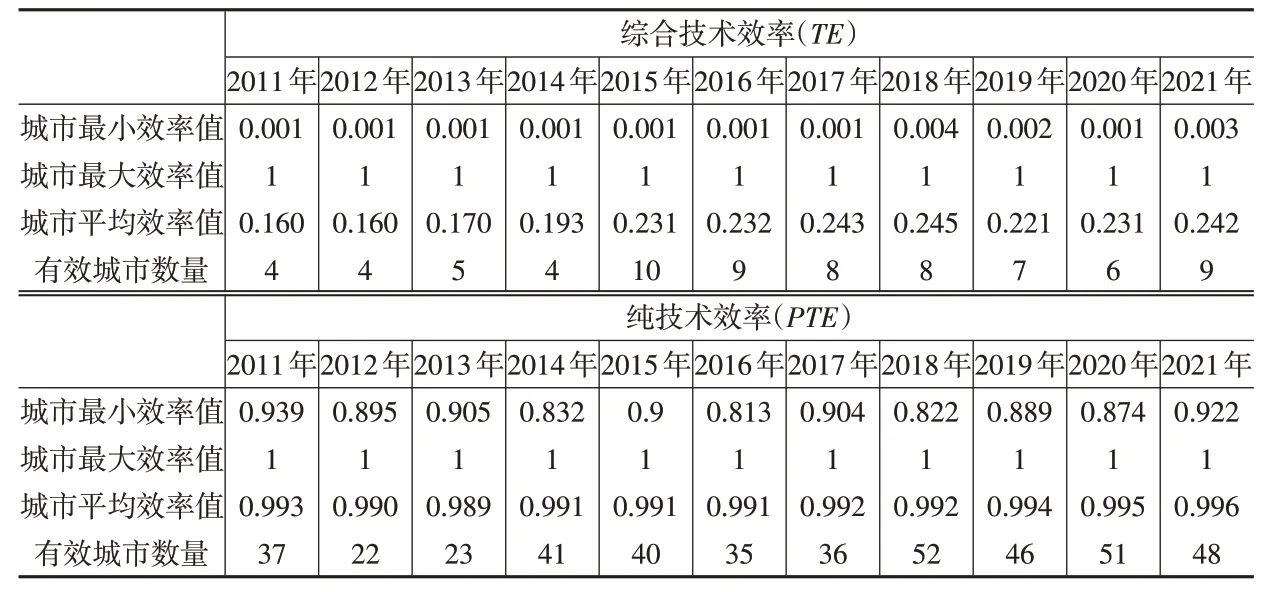
表4 城市群所辖城市财政科技投入绩效统计表（第三阶段）

由表4可知，调整科技投入变量后重新进行财政科技投入绩效运算，结果显示调整前后效率结果相差较多，其中纯技术效率（PTE）大幅增长，其203个DMU（城市）总体的平均效率水平趋近于1，接近效率前沿面；而203 个DMU（城市）总体的综合技术效率（TE）历年平均效率水平出现上升。综合技术效率处于效率前沿面上的有效城市数量在8 个左右，相对于调整前有所下降，第三阶段财政科技投入绩效均值在0.2左右，相较于第一阶段下降了0.2左右。第三阶段位于效率前沿面上的城市相较于第一阶段变动较大，各个年份处于效率前沿面上的城市有所变动，其中苏州市、深圳市在9 个年份中效率值全部为1，为效率最高的城市；宁波市曾于7个年份中效率值为1，北京市曾于5个年份中效率值为1；温州市、中山市曾于4个年份中效率值为1，这些城市在较多年份中位于效率前沿面上，是财政科技投入绩效水平较高的城市。

通过对调整后的城市群203 个DMU（城市）2011—2021年的财政科技投入综合技术效率（TE）和纯技术效率（PTE）进行加总平均，得出19 个城市群各自的效率均值，并继而计算得出国家级、区域级和地区级城市群以及中国城市群总体的效率均值（见表5）。

表5 城市群财政科技投入纯技术效率（三阶段）

2.2 空间趋势面分析

为了进一步探究我国城市群财政科技投入绩效空间演化规律，使用ArcGIS10.2 分别绘制2014 年、2016 年、2018 年和2020 年的中国城市群财政科技投入综合技术效率的空间演化趋势图（见图1）。

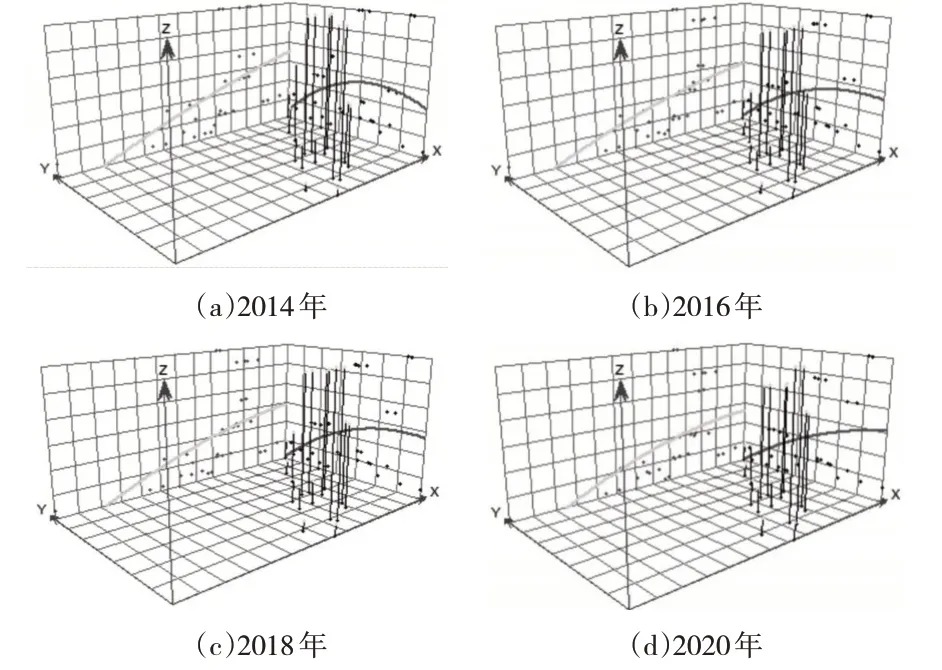
图1 空间趋势面分析图

由表5 可知，在经过调整投入变量后，纯技术效率相较于调整前有了大幅提升，各个城市群的效率均值均在0.9 以上，接近效率前沿面，但不同城市群间差异较小，不同年份间变动较少，因此将财政科技投入综合技术效率作为静态的城市群财政科技投入绩效进行空间格局分析。

由表6 可知，城市群财政科技投入平均效率值为0.176，其中高于平均效率水平的城市群有6 个，低于平均效率水平城市群有13 个，表明我国城市群间财政科技投入绩效差距较大。将城市群历年综合技术效率值加总平均并进行排名后可以发现，国家级城市群财政科技投入综合技术效率水平最高，效率得分均值为0.325，且效率提升最为强劲；区域级城市群财政科技投入综合技术效率水平略低于国家级城市群，效率得分均值为0.153；地区级城市群财政科技投入综合技术效率水平最低，效率得分均值为0.067，与国家级、区域级城市群存在较大差距，效率提升也最缓慢。城市群财政科技投入综合技术高效率区域由国家级城市群逐步向周边的区域级城市群和地区级城市群扩散，印证了当前中国城市群发展规划、发展定位的合理性。

图1中，X轴和Y轴分别指向东方和北方，ZOX 面上的趋势线和ZOY面上的趋势线分别代表了财政科技投入综合技术效率在东西、南北方向上的投影。可以看出，城市群财政科技投入综合技术效率在东西方向上呈现“东高西低”的空间分布特征，在南北方向上呈现“南高北低”的空间分布特征。

3 城市群财政科技投入绩效的时间动态演化分析

为了进一步研究城市群财政科技投入绩效在时间序列上的动态演化，运用Malmquist指数对剔除了外部环境和随机因素的投入变量与原始产出变量进行测算，并进一步对2011—2021 年中国城市群财政科技投入全要素生产率（TFP）进行分解以及动态演化分析，由于篇幅所限，仅将203 个DMU（城市）全要素生产率进行加总平均得到中国城市群财政科技投入全要素生产率演化情况，结果见表7。

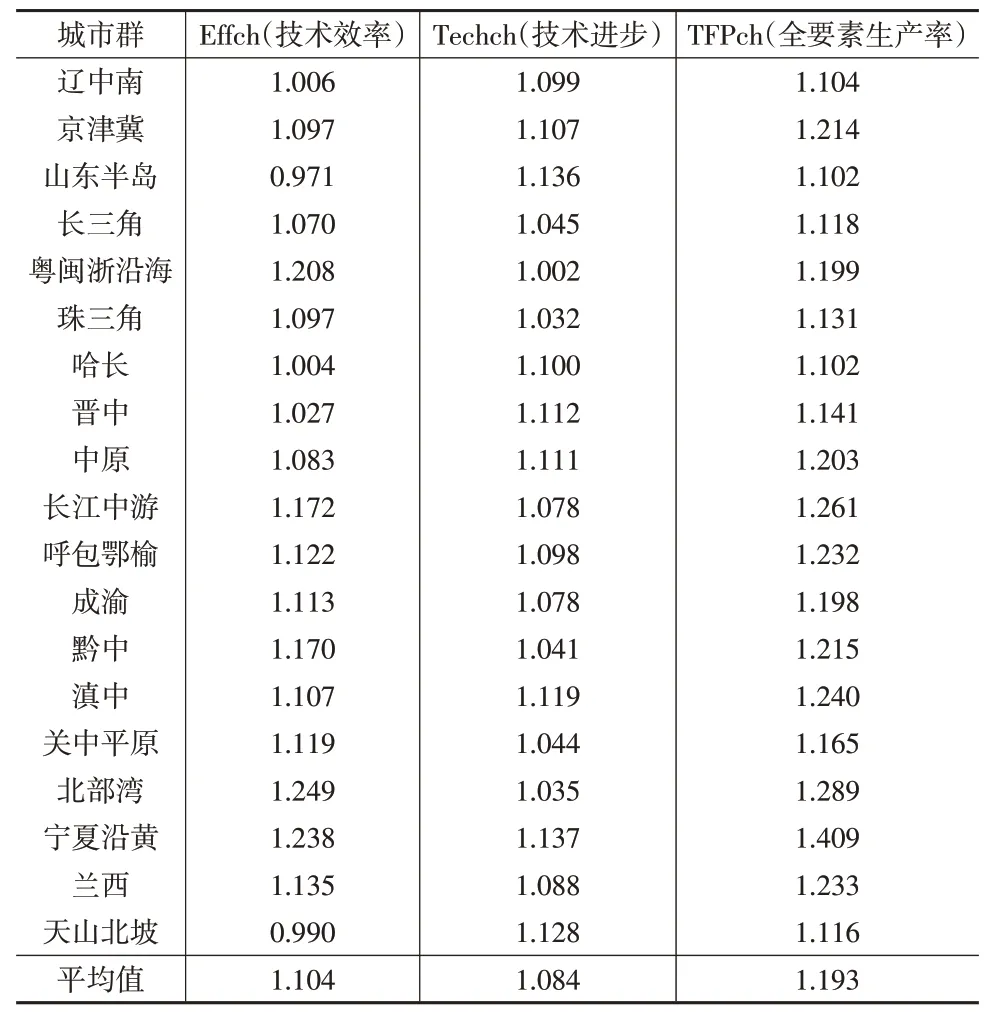
表7 城市群财政科技投入Malmquist指数及分解

由表7可知，财政科技投入全要素生产率（TFP）、技术效率变化指数（Effch）和技术进步指数（Techch）均为正数，均有不同程度的提升，其中城市群财政科技投入TFP的增长主要是源于技术效率带来的促进作用，技术进步虽然存在，但对TFP增长贡献不如技术效率进步作用大。其中宁夏沿黄城市群的年均全要素生产率最高，为1.409，代表其财政科技投入绩效提升最为迅猛，山东半岛和哈长城市群的年均全要素生产率最低，为1.102，提升较为缓慢。城市群的年平均全要素生产率为1.193，表明城市群总体的财政科技投入绩效年平均增长率为19.3%。

由表8 可知，从2011—2021 年城市群所辖城市的财政科技投入Malmquist 指数分解可知，历年城市总体的财政科技投入的技术效率变化、规模效率变化和全要素生产率变化均为上升态势，而技术进步变化和纯技术效率变化在部分年份呈现下降态势。

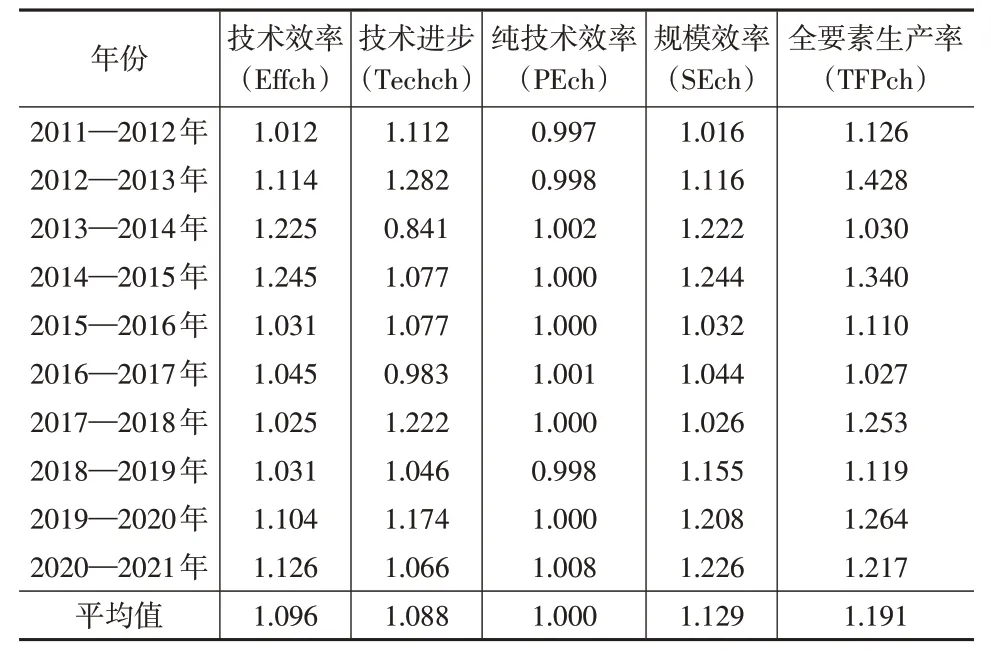
表8 城市群所辖城市财政科技投入Malmquist指数及分解

4 结论

本文以2011—2021年中国19个城市群内所辖城市为研究样本，构建三阶段DEA-Malmquist 模型，探究了中国城市群财政科技投入绩效的时空演化规律。得出以下结论：（1）中国城市群财政科技投入综合技术高效率区域由国家级城市群逐步向周边的区域级城市群和地区级城市群扩散，印证了中国城市群发展规划、发展定位的合理性。（2）中国城市群财政科技投入综合技术效率呈现“东高西低”“南高北低”的空间分布特征。（3）中国城市群总体的财政科技投入的技术效率变化、规模效率变化和全要素生产率变化均为上升态势，而技术进步变化和纯技术效率进步变化在部分年份呈现下降态势。