基于CNN-LSTM 的车辆悬挂系统故障识别方法研究

梁君海，李智强，葛 天，郑志伟

（1.中车成都机车车辆有限公司 技术中心，成都 610511；2.西南交通大学 轨道交通运载系统全国重点实验室，成都 610031）

高速铁路车辆（简称：车辆）运行在复杂多变的线路环境下，其行驶速度的提高伴随着激扰频带的加宽，使其悬挂系统的负担越来越大。随着车辆在轨运行时间的增长，其悬挂系统中的一些部件（螺旋弹簧、减振器、空气弹簧等）会产生一定程度的性能衰退，诱发诸如螺旋弹簧细微开裂、减振器轻微漏油/漏液、空气弹簧轻度漏气等早期故障，给行车安全带来潜在的危险[1]。因此，为保障车辆安全、稳定、可靠地运行，有必要对车辆悬挂系统早期故障进行及时诊断。

已有学者针对车辆悬挂系统故障对车辆动力学性能的影响进行了大量研究，研究结果表明，车辆悬挂系统早期故障的影响程度有限，人为进行故障判别较为困难[2-4]。此外，由于车辆悬挂系统模型的非线性，无法直接将故障类型与动力学性能表现联系起来，因此，有学者通过提取车辆动力学性能参数特征来进行悬挂系统故障识别。苏宇婷等人[5]通过提取车体加速度信号时频域特征，结合流形学习特征降维，成功实现了抗蛇行减振器故障、悬挂系统空气弹簧失气和横向减振器故障的识别；李晓[6]使用SIMPACK 平台建立高速列车动力学模型，提取仿真得到的构架加速度信号的信息熵、信息㶲等特征，结合支持向量机（SVM，Support Vector Machine）训练得到了故障识别及定位模型，实现了对空气弹簧、横向减振器等转向架关键部件的故障识别及定位；李昌喜[7]使用参数优化变分模态分解对转向架关键部件的故障振动信号进行预处理，提取最优分量的多尺度样本熵特征，构成特征向量，结合SVM 实现了转向架关键部件故障识别；为弥补单通道输入故障特征有限的不足，刘佳龙[8]采用多通道特征向量作为输入，结合参数优化SVM，实现了高速列车转向架的故障诊断。

虽有不少学者结合人工智能提出较有效的车辆悬挂系统故障诊断模型，但是由于这些方法大多采用基于特征工程的数据驱动模型，较依赖专家知识。为此，本文提出一种结合卷积神经网络（CNN，Convolutional Neural Network）和长短时记忆（LSTM，Long Short Term Memory）模型的车辆悬挂系统故障识别方法，在不依赖人工经验的情况下实现端到端的智能故障识别。

1 相关技术

1.1 CNN

CNN 是一种具有卷积结构的深度神经网络，它的基本结构包括输入层、卷积层、池化层、全连接层与输出层[9]。CNN 中的数据处理主要分为过滤阶段和分类阶段。数据过滤阶段由卷积层和池化层完成，这一阶段的目的是特征学习和提取；数据分类阶段由全连接层完成，这一阶段的目的是数据对应类别判定。分类阶段的全连接层与输出层通常采用Softmax 函数，用于计算多分类问题的概率输出。

1.2 LSTM 模型

LSTM 模型的基础结构是循环神经网络（RNN，Recurrent Neural Network）模型，可解决RNN 模型的长依赖问题[10]。由于时序数据的增多，RNN 模型无法有效利用之前时刻的历史信息，导致发生梯度消失与梯度爆炸，即当网络层数增加、时间序列数据距离增大时，后面神经单元对前面神经单元的感知能力降低，导致遗忘前面信息的问题，无法有效利用历史信息。在RNN 的基础上，LSTM 模型通过增加新的记忆单元c，解决RNN 模型存在的梯度消失与梯度爆炸问题，提高模型可靠性，同时，LSTM模型具有反馈结构，可在历史信息中挖掘数据的特征，擅于处理时序数据的预测问题。

LSTM 模型由多个存储块组成，每个存储块都有遗忘门、输入门和输出门。所谓的“门”结构是一个全连接神经网络，使用Sigmoid 函数作为激活函数，并输出0 到1 之间的值。可将存储块作为一个细胞，LSTM 模型依赖于这些“门”，允许输入特征在每个时刻选择性地影响细胞状态，从而实现对当前时刻神经网络输出的控制。具体来讲，遗忘门决定细胞状态中哪些信息应该被删除，哪些信息应该被保留；输入门的作用是向细胞状态加入新内容；输出门的作用是从当前的细胞状态中选择有用信息并将其显示为输出。传统的LSTM 模型的反向传播思路和RNN 模型的反向传播思路一致，均采用梯度下降法对网络参数进行更新，主要步骤是对所有参数基于损失函数的偏导数进行计算。

2 车辆悬挂系统故障识别方法

2.1 CNN-LSTM 模型

本文针对车辆悬挂系统的故障振动信号，设计一种CNN-LSTM 模型，其模型架构如图1 所示，具体参数设定如表1 所示。该模型将CNN 和LSTM 模型结合成一个统一的网络结构，使之兼具CNN 和LSTM 模型的优势；利用3 层卷积和1 层池化结构来提取数据的空间特征，再采用1 层LSTM 模型提取数据的时间特征；采用全连接层对CNN 和LSTM 模型提取的局部时空特征进行全局学习；最后利用Softmax 激活函数实现对不同故障的分类识别。

表1 CNN-LSTM 模型参数设定

图1 CNN-LSTM 模型架构

2.2 方法流程

车辆悬挂系统故障识别模型的具体流程如下。

（1）数据采集：建立车辆-轨道耦合动力学数值仿真模型，并基于该动力学模型模拟不同工况下车辆悬挂系统故障，获取大量的悬挂元件故障数据。

（2）数据标准化：考虑到输入数据来自车辆的不同部件，应对数据进行标准化，将原始振动加速度信号进行标准差标准化，计算公式为

式（1）中，xi是原始序列的i个数据点；yi是经过标准化转换后的新序列的数据点；是原始序列的平均值；s是原始序列的标准差；n是原始序列的采样点数。经标准化后的新序列的平均值为0，标准差为1。

（3）模型训练：通过数据采集获取的故障数据，训练CNN-LSTM 模型，采用准确率（Accuracy）作为评价指标来考察模型的精度，计算公式为

式（2）中，f(xk) 是模型的预测值；yk是模型的真实值；I是判定预测值是否等于真实值的函数，若相等则函数值为1，否则为0。

（4）预测评估：将标准化后的一维仿真振动信号输入到训练好的CNN-LSTM 模型中，实现对车辆悬挂系统故障类型的识别，并用于指导车辆运行和维护。

3 试验搭建与结果分析

3.1 数据采集

基于SIMPACK 平台，建立CRH2 型动车组的车辆-轨道耦合动力学模型，根据研究目的对其进行适当简化，将车体、构架、轮对等均视为刚体，忽略各部件的弹性变形，同时不考虑车辆牵引和制动2 种运行工况。CRH2 型动车组的车辆-轨道耦合动力学模型，如图2 所示，由1 个车体、2 个构架、4个轮对、8 个轴箱，共计15 个刚体组成。振动加速度计安装位置，如图3 所示，前、后构架均设置1 个加速度计，收集构架横向和垂向加速度信号；分别在1 位轴和4 位轴每个轴箱处设置1 个加速度计，收集轴箱横向和垂向加速度信号；在车体的前、后心盘处各设置一个加速度计，收集车体的三向加速度信号。

图2 CRH2 型动车组的车辆-轨道耦合动力学模型

图3 加速度计安装位置及设置

仿真试验共设置3 种类型的车辆悬挂系统故障，分别为钢弹簧断裂、减振器漏油及空气弹簧失气。其中，钢弹簧为一系悬挂系统的元件之一，当弹簧外圈断裂时，由弹簧内圈提供承载作用；减振器包括一系垂向减振器、二系垂向减振器及二系横向减振器，当减振器漏油时，其阻尼接近完全失效；空气弹簧是二系悬挂系统的元件之一，当空气弹簧失气时，应急橡胶堆提供承载。因本文研究的是车辆悬挂系统早期故障诊断，因此，仿真时钢弹簧断裂故障程度设置为0.5，减振器故障设置为0.01。

3.2 试验搭建

训练数据来源于车辆轴箱、构架和车体上安装的加速度计收集到的振动加速度信号，采样频率为300 Hz。此外，基于车辆-轨道耦合动力学模型分别模拟在150 km/h、200 km/h 和250 km/h 等3 种不同恒定速度下的运行，仿真时间历程始终为50 s。将不同工况条件下每1 s 的时间序列作为一个训练样本，并按照8∶2 划分为训练数据集和测试数据集。使用交叉熵损失函数和Softmax 分类器，超参数设置为：学习率为0.001，随机失活率为0.2。

3.3 试验结果分析

3.3.1 同一速度等级下车辆悬挂系统故障识别

在200 km/h 速度等级下对车辆悬挂系统进行3类试验。试验1：一系悬挂系统垂向故障训练识别，包括健康、钢弹簧故障和一系垂向减振器故障等3种状态；试验2：二系垂向悬挂系统故障训练识别，包括健康、空气弹簧故障和二系垂向减振器故障等3 种状态；试验3：二系悬挂系统横向故障训练识别，包括健康、空气弹簧故障和二系横向减振器故障等3 种状态。以上3 类实验中，每类实验每种状态都包含160 个训练样本和30 个测试样本，训练样本数量共计480 个，测试样本数量共计90 个。

3 类试验的分类准确率和损失函数如图4 和图5所示。经过250 次迭代计算后，试验1 的故障识别准确率为73%，训练损失值为0.816；试验2 的故障识别准确率为84%，训练损失为0.709；试验3 的故障识别准确率明显提高，为98%，损失值也降至0.561。实验结果表明，本文的故障识别方法在同一速度等级下具有较高的准确率，能够有效地进行车辆悬挂系统故障诊断。其中，二系悬挂系统的故障识别准确率高于一系悬挂系统，造成这一现象的原因，主要是由于一系悬挂系统受力更加复杂，当一系悬挂系统发生故障时，故障信号更易被淹没。另外，车辆悬挂系统横向故障的识别准确率远高于垂向故障，主要原因在于横向故障时，对车辆构架横向振动影响较大，引起的信号波动更为明显。

图4 准确率变化曲线

图5 损失函数变化曲线

3.3.2 不同速度等级下车辆悬挂系统故障识别

为进一步验证所提模型在不同速度等级下的有效性，考虑3 种速度等级，进行以下实验。

试验4：在150 km/h、200 km/h、250 km/h 速度等级下进行一系悬挂系统垂向故障训练识别，分别选取健康、钢弹簧故障和一系垂向减振器故障等3种状态；试验5：在150 km/h、200 km/h、250 km/h速度等级下进行二系悬挂系统垂向故障训练识别，分别选取健康、空气弹簧故障和二系垂向减振器故障等3 种状态；试验6：在150 km/h、200 km/h、250 km/h 速度等级下进行二系悬挂系统横向故障训练识别，分别选取健康、空气弹簧故障和二系横向减振器故障等3 种状态。以上3 类试验，由于考虑了3 种速度等级的情况，每类试验每种状态都包含160 个训练样本和30 个测试样本，训练样本数量共计1 440 个，测试样本数量共计270 个。

3 类试验的分类准确率和损失函数如图6、图7所示，经过250 次迭代计算后，在不同速度等级下，试验4 的故障识别准确率为76%，训练损失为0.784；试验5 的故障识别准确率为87%，训练损失为0.665；试验6 的故障识别准确率为99%，损失值为0.575。试验结果表明，本文的故障识别方法针对不同速度等级下的车辆悬挂系统故障识别仍保持较高的准确率，具有良好的鲁棒性。

图6 准确率变化曲线

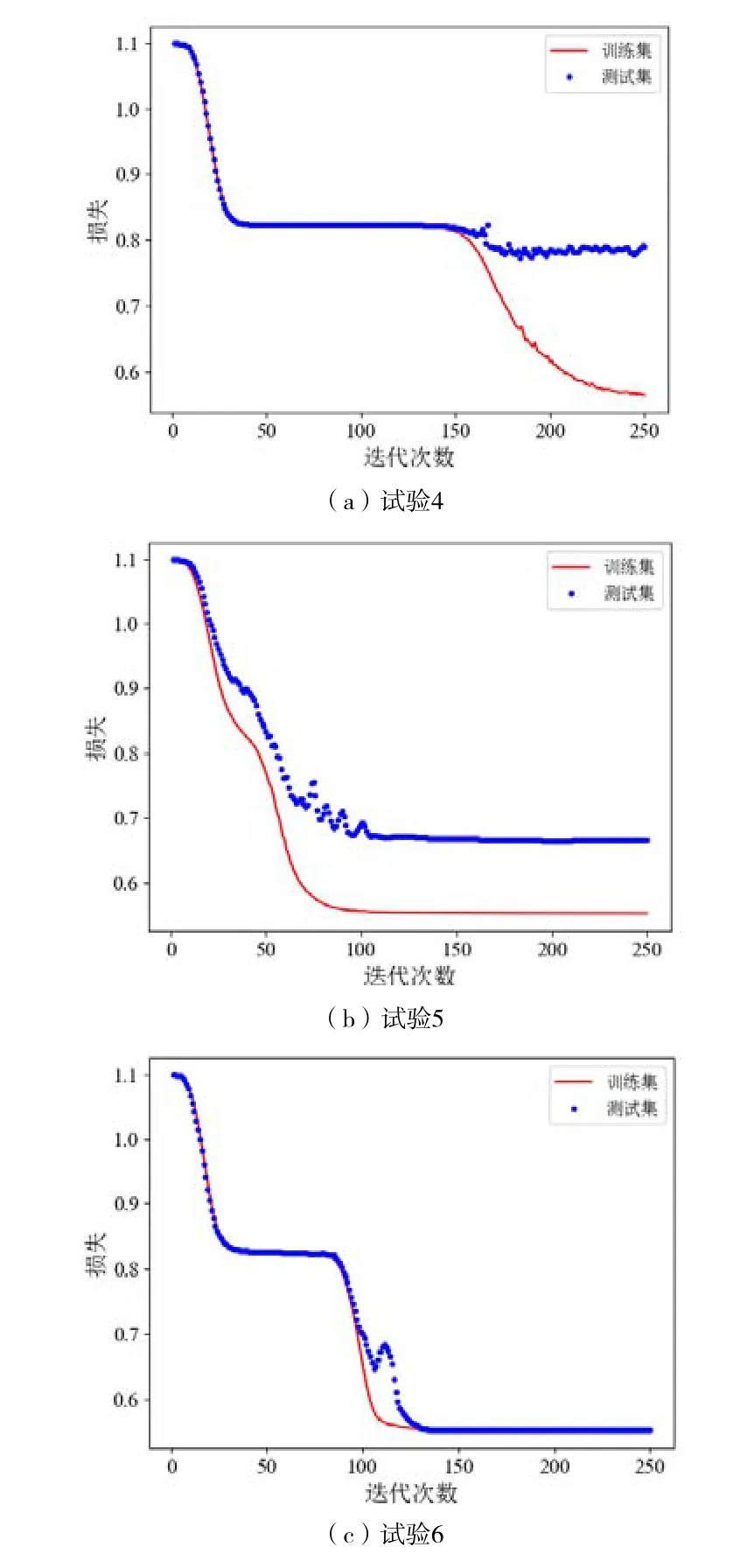
图7 损失函数变化曲线

综上，相对于传统的主流方法，本文提出的方法基于原始数据驱动，不需要通过人工经验对数据进行特征提取，在简化诊断流程的基础上，仍能够保持较高的故障识别率，为车辆悬挂系统智能故障诊断的研究提供新的思路。

4 结束语

本文在建立了车辆-轨道耦合动力学模型的基础上，利用仿真数据提出了基于CNN-LSTM 模型的车辆悬挂系统故障识别方法，结合了CNN 和LSTM 模型的优势，能够提取原始振动信号中的故障特征，有效减少人工特征提取过程中带来的不确定性。通过试验得出以下结论：

（1）在同一速度等级下，本文方法可直接从原始振动信号中识别故障类型，且准确率较高；

（2）在不同速度等级下，本文方法仍能保证较高的准确率，具有良好的鲁棒性。

（3）由于一系悬挂系统受力较复杂，二系悬挂系统的故障识别准确率一般高于一系悬挂系统。