基于混合粒子群算法的圆柱型电磁铁优化设计
王晨皓,林何,盛晓超
(1.西安工程大学机电工程学院,陕西西安 710048;2.西安工程大学西安市现代智能纺织装备重点实验室,陕西西安 710048)
0 前言
电磁铁是磁悬浮系统中的关键部件,大至磁悬浮列车,小到磁悬浮轴承,其性能高低直接决定了整个系统的性能[1-2]。在一个控制系统中,电磁铁的响应速度不够快,或者是产生的电磁力不满足要求,都会使整个系统的性能下降[3-4],同时被吸引物所受到的电磁力是影响系统动态响应的重要因素[5]。因此,对电磁铁的性能进行研究非常有必要。
鉴于电磁铁在悬浮系统中的重要性,许多学者对其结构和特性进行了研究,用以满足技术的发展需要:ABBOTT、OSTING[6]通过优化无芯电磁铁限制其设计空间达到最佳总体设计;胡经文等[7]研究了基于磁源重构的本安型电磁铁,优化后的电磁铁动态性能明显提升;董润鹏等[8]采用的优化算法使优化后的电磁铁完成目标行程所需电流更小;DING等[9]提出一种新的电磁模块结构设计,以解决磁饱和问题;蔡胜年等[10]基于物理原型计算并采用Ansoft和AMESim仿真软件,提高了所设计比例电磁阀的动态特性和稳态精度;HWANG等[11]提出一种采用平行铁芯结构的多极电磁铁的设计概念,扩大了电磁铁适用领域;郭东军等[12]设计一种磁力大、行程长的双线圈电磁铁,在ANSYS Electronics Desktop的2D模块中进行仿真分析,得到电磁铁自身结构参数对电磁力的影响。上述研究大部分都是研究电磁铁各部分参数单独对电磁力的影响,鲜有通过磁路对电磁铁各参数间相互作用影响电磁力的研究,而且目前已有的研究大多都是针对工程中常用的电磁铁比如电磁阀电磁铁、比例电磁铁等的研究,而像应用于磁悬浮系统中的圆柱型电磁铁研究较少。
研究针对磁悬浮系统中小型电磁铁,描述该类电磁铁的结构和工作原理,首先采用高斯计实测电磁铁特定位置的磁感应强度值,再通过有限元仿真方法得到相同位置下的磁感应强度,对比两组数据说明有限元仿真的准确性。其次通过仿真找到电磁铁电磁力及磁感应强度与结构参数的对应关系,采用简化数学模型的计算值与仿真值作对比,验证数学模型的准确性,并分析圆柱型电磁铁磁路,建立了电磁铁磁阻力模型。最后提出一种改进的多目标优化方法,优化电磁铁设计时的结构参数,找出制约电磁铁磁阻力的因素,设计出合理的电磁铁模型,并通过仿真验证其综合性能。因此,在有尺寸制约的条件下找出电磁线圈各个条件间的最优解成为作者的首要目标。
1 电磁铁结构及磁路分析
1.1 电磁铁结构
电磁铁主要由骨架、铁芯和线圈组成。根据铁芯的结构可将电磁铁分为E型、尖端型、圆柱型、I型、C型等多种形式[13]。其中圆柱型、E型、I型、尖端型主要产生竖直方向的磁场,E型、I型尖端型电磁铁磁力线闭合在空气中。而圆柱型电磁铁磁力线闭合在物体内部,加之在设计电磁铁时选用的都是导磁性良好的材料,圆柱型电磁铁在相同的电流下有更好的磁感应强度,在磁悬浮系统中有更广泛的应用。
1.2 磁路分析
将电磁力作为优化目标首先要分析易对电磁力造成影响的参数,磁路长度、磁极面积、空气漏磁通以及铁芯材料的磁滞特性都是影响电磁力的重要因素。其中,分析磁路能更好地建立电磁铁数学模型,对理解电磁铁工作原理也有益处。磁路长度采用平均磁路法分析,取电磁铁和气隙的几何中心进行计算,此次仿真采用的是DT4电工纯铁,它具有良好的导磁性,在一定范围内铁芯处的磁感应强度B与磁场强度H呈线性关系。
高磁导率的铁磁性材料有良好的导磁性[14],形成的磁力线更密集,磁通(主磁通和漏磁通)经过的闭合路径叫做磁路。根据物体材料特性的差异可以把磁路细分成几段,使每段都有相等的截面积和相同的磁介质。假设在这样的磁路中磁场强度各处都相等,且其方向与磁路经过的方向一致时,在任何横向截面上,磁通都是均匀分布的[15],当线圈中通入电流时,便形成一定的磁势。在该磁势的作用下,沿着电磁铁铁芯、工作气隙形成一个类似电路的磁通回路,在此回路中的为主磁通,产生电磁力;还有部分为空气漏磁通,一部分是过磁极面积形成的回路,一部分是在空气中形成的回路,相较于主磁路磁通较小。文中优化设计后期服务于磁悬浮系统,可通过控制方法弥补忽略的空气漏磁通,故不做详细研究。根据上述分析得出圆柱型电磁铁的等效磁路,如图1所示。

图1 圆柱型电磁铁等效磁路
图中:R1为圆柱型电磁铁磁阻;R2为被吸引物体磁阻;Rs为空气中漏磁阻;Rδ为气隙磁阻。
根据基尔霍夫第二定理有:
NI=φR
(1)
式中:N为线圈匝数;I为线圈电流;φ为主磁通;R为磁阻。则圆柱型电磁铁的磁路公式为
NI=φ(R1+R2+Rs+Rδ)
(2)
磁阻的计算公式为
(3)
式中:L为磁路长度;μ为物体的磁导率;S为磁路面积。文中磁路主磁通有如下表达:
(4)
式中:S1为圆柱电磁铁的磁极面积;S2为被吸物体的磁极面积;Sδ为气隙截面面积。
1.3 电磁铁磁场分析
电磁铁的磁场集中在铁芯、气隙及磁路闭合的区域。为简化计算,假设铁芯的磁导率为固定值且工作时不考虑材料的磁滞效应和涡流效应,不考虑电感对磁场的影响,且磁场分布稳定。仿真参数设置:励磁线圈匝数为1 000匝,通电电流为1 A,励磁线圈为QZ-2/1300.35,铁芯采用DT4型电工纯铁。建立三维模型进行磁感应强度仿真计算,同时采用高斯数字特斯拉计测量该电磁铁在z轴方向上产生的磁感应强度Bz,将测试结果与仿真值进行对比,建模计算结果和实验吻合良好,证明仿真计算的准确性。图2所示为线下购买的电磁铁实测和仿真结果对比。

图2 所购电磁铁实测和仿真结果对比
1.4 电磁铁结构分析
由于电磁铁使用的特殊性,其设计尺寸都存在一定的取值范围,且铁芯过大会导致线圈匝数减少,磁力减小;匝数过多会导致磁饱和,还要保证内外环面积相等的设计原则,故设定铁芯半径Rn取值范围为1~14 mm。铁芯半径确定以后根据磁路定理磁极面积相等得到圆柱型电磁铁内环半径,根据内外环半径差即磁轭厚度C得到顶部高度hd,已知窗口宽度bk,线圈匝数N的计算公式为
(5)
式中:bk为窗口宽度,mm;hk为窗口高度,mm;fk为线圈填充系数;d为漆包线直径,mm。根据漆包线规格及参数,当铜导线直径d标称为0.35 mm,线圈填充系数fk=0.646。线圈电磁铁各参数如图3所示。

图3 内外部结构尺寸
2 电磁铁优化设计
2.1 优化目标
稳定和快速响应是评价电磁线圈性能的关键指标。根据磁悬浮稳定悬浮的特点,在物体悬浮初始,需要电磁线圈提供较大的电磁力迅速达到指定位置,又需要电磁线圈提供能够使物体稳定悬浮的电磁力。优化内部结构参数,通过提高电磁力提高系统的运行效率,所以优化目的是在相同的电流激励下,使优化后的电磁铁产生的力满足使用要求。同时,受磁悬浮系统中结构尺寸的限制,外部结构尺寸不能无限加大,因此,优化重点就是在有尺寸制约的条件下找出电磁线圈各个条件间的最优解。
2.2 磁力模型
电磁力不是一个理想的稳定数值,影响电磁力的主要参数很多,通常通过假设对电磁力的计算进行简化,忽略气隙中的磁漏和空气中的磁漏。根据麦克斯韦电磁力方程,电磁力F可表示为
(6)
其中:
(7)
式中:F为电磁吸力,N;Bδ为气隙磁感应强度,T;φδ为主磁通,Wb;S为磁极表面总面积,m2;μ0为空气磁导率,值为4π×10-7H/m。
则文中的优化表示为
(8)
3 电磁铁仿真分析
ANSYS Maxwell是一款主流的电磁仿真软件,在设计和分析马达、传感器、变压器和其他相关电磁场的电气设备中可靠度很好,特别适用于在研制初期降低生产成本。其中Maxwell3D可以有效地分析结构中不受时间影响的静磁场,并且可以应用于恒定的激励源,如永磁体、电流、电压以及各种外部模拟的复杂输入,从而精确地计算出电磁力、损耗、电感等相关参数,利用Maxwell的电磁场求解器可以加快设计时间,提高精准度,实现对结构的有效控制。
3.1 仿真相关参数设置
在Maxwell中建立三维模型,其中铁芯为电工纯铁(DT4),磁化曲线如图4所示,铜线电导率为系统默认,空气相对磁导率为1,空气域为三维模型的5倍,内网格为3 mm,外网格为5 mm,迭代次数为8次,误差小于10%,激励源为电流源。

图4 铁芯材料B-H曲线
3.2 仿真结果及分析
电磁铁的静态特性由其本身的结构决定,通过控制变量的方法对其中某一个参数进行仿真得到其对磁感应强度的影响,仿真结果如图5—8所示。
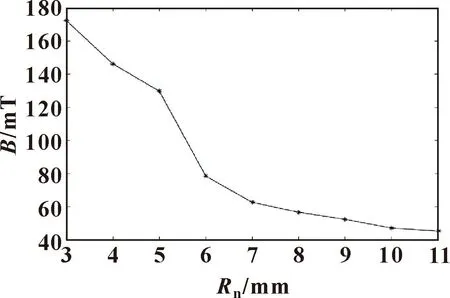
图5 铁芯半径与磁感应强度关系
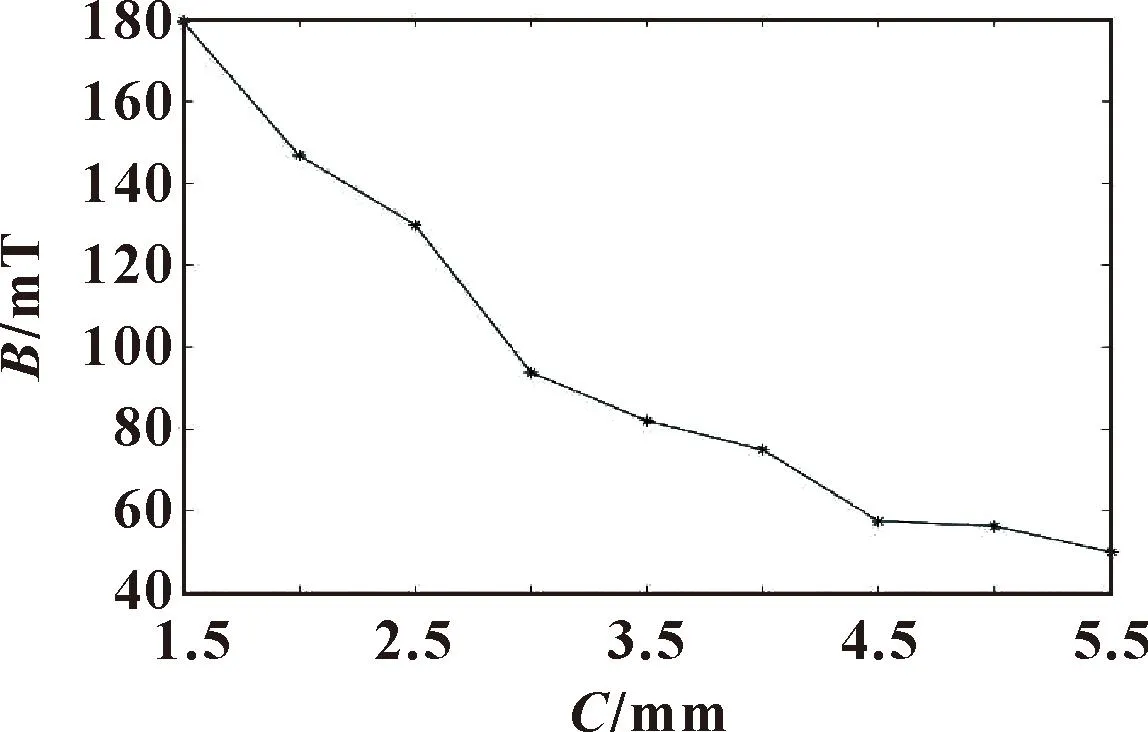
图6 磁轭厚度与磁感应强度关系

图7 顶部高度与磁感应强度关系

图8 窗口高度与磁感应强度关系
图5—8分别为铁芯半径Rn、磁轭厚度C、顶部高度hd、窗口高度hk与磁感应强度B的关系。在设计中,应在允许的情况下减小磁轭厚度,磁轭厚度越小,有效区域磁感应强度越大;线圈的绕制高度和绕制厚度对磁感应强度的影响较大,需要合理设计。同时铁芯的半径也应与线圈匹配,磁芯设计太粗,会使磁化难度增加,削弱磁感应强度,磁芯设计过细则造成磁芯达到饱和时磁感应强度仍然较小,铁芯自身的结构参数对其磁感应强度的变化都有着不小的影响。单一目标变化不能满足磁悬浮中磁感应强度以及磁力的需要,另外磁悬浮系统中整体系统要求电磁铁外部结构是有限的,单一结构参数的变化会导致其他结构参数的变动,最终影响磁感应强度变化,影响磁力,导致系统性能不满足要求。
4 电磁铁优化结果分析
文中提出的优化方法是基于粒子群改进的混合粒子群算法,该算法结合了遗传算法的“交叉(Crossover)”和“变异(Mutation)”操作。粒子群优化算法(Particle Swarm Optimization,PSO)是一种演化计算技术,该算法最初是受到鸟群不可预测的集群活动的启发,进而利用群体习性建立的一个算法模型[16]。
由于粒子群算法在面对优化问题中局部最优的欺骗性太强时,容易陷入局部最优解。对于已经陷入到局部最优的情况,一般是采取“跳出”或“重启”两种方法进行再次寻优,也就是在当前得到的最优基础上向其他方向搜索,或者忽略当前得到的最优解并在新的区域重新进行搜索。简而言之,避免陷入上述欺骗性太强的局部最优的方法就是随机,而“交叉”和“变异”的引入很好地增加了群体的随机性,在重新完成寻优之后的新粒子适应度值好于旧粒子时才更新粒子[17],即得到最优解。基于MATLAB与Maxwell的协同仿真流程如图9所示。

图9 MATLAB与Maxwell协同仿真流程
单一目标参数优化是选取有限个实验点进行计算分析,采用统计法找出目标参数与优化目标之间的函数关系,通过关系寻找最优点。但是该方法没有考虑其他参数对优化目标的影响,未能达到一个动态平衡,即各参数最优使电磁力和磁感应强度最大。
为了更好地对电磁铁结构进行参数优化,本文作者采用MATLAB与Maxwell协同仿真的方法,在各参数变化范围内对电磁力进行优化。针对多目标优化问题,通过权重系数转化为单目标问题进行处理,面向的主要问题是解决磁悬浮中力的速度与稳定性的问题,因此,将磁感应强度、窗口宽度等变量统一表述为以电磁力为目标的函数。将多目标转化为单目标后,在Maxwell中建立三维模型,其中铁芯为电工纯铁(DT4),磁化曲线如图4所示,铜线电导率为系统默认,空气相对磁导率为1,空气域为三维模型的5倍,内网格为3 mm,外网格为5 mm,迭代次数为8次,误差小于10%,再由混合粒子群的优化过程进行计算。其初始参数如表1所示,优化结果如表2所示。

表2 混合粒子群参数优化结果
对比混合粒子群优化算法得到的电磁力与单目标优化得到电磁力在不同悬浮气隙下的数值,绘制该模型在上述假定状态下计算值与仿真值对比曲线图和结果对比表,如表3所示。

表3 优化结果对比
可以看出:未考虑磁滞影响时,电磁力随着气隙的增大而减小;对电磁铁进行单目标优化时,优化后电磁力有明显提升;相同激励条件下,采用混合粒子群算法得到的电磁力比单目标优化得到的电磁力综合提升20%,在不同悬浮气隙下,优化后的电磁铁电磁力均比单目标要好得多,达到了优化目的。
5 结论
本文作者提出磁悬浮系统中电磁铁的优化方案,采用了MATLAB与Maxwell协同的方式进行仿真分析,结果表明电磁铁铁芯以及各种内部结构参数与电磁力的关系。通过实验和仿真对比验证了有限元方法的准确性。通过分析电磁铁磁路,建立了电磁铁磁力的数学计算模型;以电磁力为优化目标,采用混合粒子群优化算法,得到最优参数,并用仿真验证了多目标优化设计电磁铁的合理性,计算结果与仿真结果吻合,综合性能最好,说明采用混合粒子群优化算法对该类模型进行多目标优化的方法是可行的。圆柱型电磁铁电磁力数学模型的建立,为进一步提高电磁铁在各类磁悬浮精密运动控制中的应用提供了参考,为其他类似多参数问题解决提供了优化思路。

