主动悬架自适应容错滑模控制研究

赵培通

（青岛大学机电工程学院，青岛 266071）

0 引言

车辆主动悬架一般由传感器、作动器、控制器及动力源组成[1]。由于车辆主动悬架可通过作动器产生的作动力降低路面输入激励对平顺性和操稳性的影响，因而受到广泛关注[2]。目前在主动悬架各元器件状态完好前提下的控制算法研究已相对成熟，但在车辆实际使用过程中，某些元器件由于长期使用或运行环境恶劣难免会出现故障[3]。作动器作为主动悬架的最核心部件，其是否存在故障会直接影响主动悬架系统的主要控制性能，因而研究主动悬架系统的作动器容错控制具有重要的理论价值和应用前景。

目前，主动悬架容错控制主要分为主动容错控制和被动容错控制[4]。杨柳青等以实现主动悬架容错控制为目标，设计了一种基于H2/H∞的最优控制器，解决了作动器故障等问题[5]。王荣蓉等考虑作动器故障，针对整车主动悬架设计一种考虑有限频率约束的H∞鲁棒容错控制器，提高了车辆的乘坐舒适性和操纵性[6]。文献[7]将执行器故障建模为由齐次马尔可夫链控制的随机变量，设计了一种H∞容错控制器。高振刚等针对作动器故障，提出了一种基于故障补偿思想的主动悬架容错控制算法，提高了车辆的控制可靠性[8]。寇发荣等以实现电磁混合悬架作动器主动容错控制功能为目的，采用未知输入观测器获取状态观测值对悬架进行故障诊断，同时采用LQG控制器对悬架系统进行力补偿，提高了主动悬架系统的鲁棒性[9]。孙晋伟等设计了主动悬架二阶滑模控制算法，较传统H∞算法更有效地提升了悬架系统的可靠性[10]。

在主动悬架作动器故障发生时，为了保障行驶过程中悬架系统的控制可靠性，本文提出了一种自适应容错滑模控制器，使其对故障不敏感。首先建立了1/4主动悬架系统模型与理想天棚参考模型，针对作动器失效后所产生的增益故障，搭建了作动器恒增益故障模型，在滑模控制算法的基础上，本文结合自适应控制理论设计了自适应容错滑模控制器，并通过仿真试验验证了所设计控制器的有效性。

1 悬架动力学模型

1.1 1/4主动悬架建模

车辆1/4模型描述了单个等效车轮的垂向运动，它可以简化为包含一个作动器和被动悬架组件的二自由度1/4 主动悬架模型（图1）。由于本文旨在分析悬架执行器故障后的垂向动力学性能，因而选用1/4主动悬架模型作为被控对象进行分析。由牛顿第二定律可知，可建立二自由度1/4 主动悬架的运动方程。

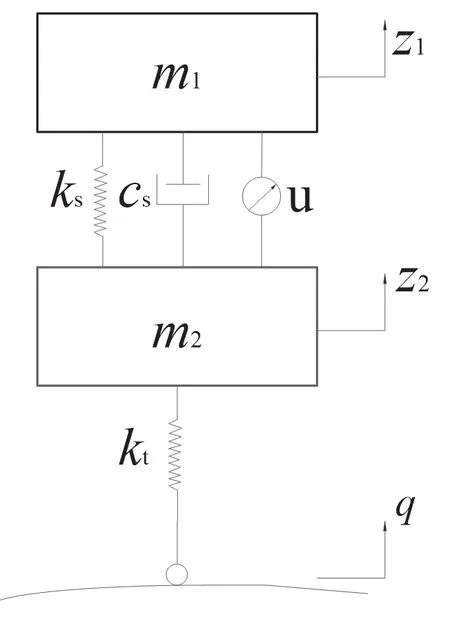
图1 二自由度主动悬架模型

式中：m1为簧上质量；m2为簧下质量；z1为簧上质量相对于平衡位置的位移；z2为簧上质量相对于平衡位置的位移；q为路面的激励位移；ks为悬架等效弹簧刚度；cs为等效阻尼系数；kt为轮胎的等效垂向刚度系数；u为作动器输出的补偿力。

分别定义状态变量x1=z1，。状态向量x=[x1x2x3x4]，系统的运动方程改写为状态空间表达式如下：

1.2 故障模型

在车辆主动悬架系统中，作动器产生主动力作用到悬架闭环系统中，但作动器可能会由于受到磨损或意外的障碍导致出现恒偏差、增益变化等不同的故障，致使作动器不能输出理想的控制力。为了便于对作动器故障进行分析，本文对故障描述进行简化，构建了作动器恒增益故障模型。作动器输出的实际控制力u计算如下：

式中：uc为作动器输出的理想控制力；σ为作动器的故障因子，0＜σ≤1。

当σ=1时表示作动器无故障；当0＜σ＜1时，表示作动器发生部分失效故障；σ=0时，表示作动器发生完全失效故障。

1.3 理想天棚参考模型

理想天棚控制假定车身与假想的天棚固连，实际情况下，在车辆运动过程中无法实现。但由于其优越的控制性能，通常被用作车辆悬架控制的动态参考模型。理想天棚参考模型如图2 所示，结合牛顿第二定律可得天棚参考模型的动力学方程为：

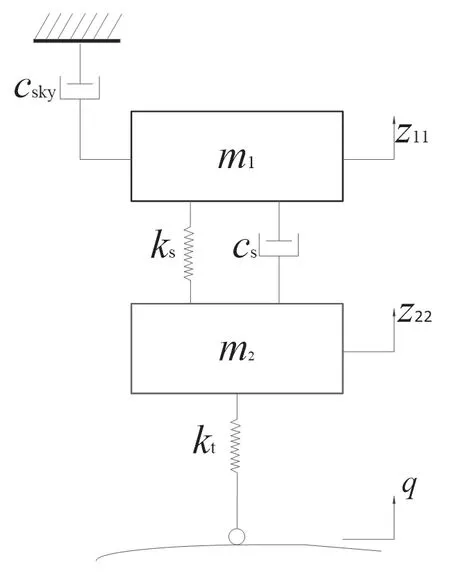
图2 理想天棚参考模型

式中：z11为理想天棚参考模型的簧上位移；z22为簧下位移；csky为天棚阻尼器阻尼系数。

而理想天棚参考模型中的簧上质量、簧下质量、等效弹簧刚度、等效阻尼器系数与车轮等效垂向刚度系数分别与1/4 主动悬架模型中相应参数相等。

2 自适应滑模容错控制器设计

将故障模型（3）带入式（2），则系统的状态空间表达式为：

本文选取理想天棚参考模型的簧上位移z11作为1/4主动悬架系统簧上质量垂向位移的理想值，定义簧上质量垂向位移的跟踪误差与簧上质量垂向速度的跟踪误差如公式（6）和公式（7）所示：

式中：e为垂向位移的跟踪误差；xd为簧上质量垂向位移的理想值，xd=z11；为簧上质量垂向速度的跟踪误差。

设计滑模面函数如公式（8）所示：

式中：c为控制参数，且c＞0。

那么其导数计算如下：

令δ=σ/m1，取p=1/δ，选取Lyapunov 函数为：

对V进行求导可得下式：

此时取：

式中：η为一个控制参数，η＞0；k是一个控制参数，k＞0；sgn(.)为符号函数，当s≥0时，sgn(s)=1；当s＜0时，sgn(s)=-1。

为防止抖振，控制器采用如公式（13）所示的饱和函数sat(s)替代sgn(s)，式中Δ为边界层。

此时

将公式（14）式带入公式（11）得：

设计控制率如下：

将公式（16）带入公式（15）得：

由公式（17）可得：

即

当t→∞时，由于V(∞)有界，则有界，根据Barbalat 引理知，当t→∞时，s→0，从而e→0 ，→0。

3 仿真验证分析

在Simulink 中搭建1/4 主动悬架系统仿真模型，选取的悬架系统参数如表1所示。选取B级随机路面作为路面激励进行仿真试验，最后选取跟踪理想天棚参考模型的传统滑模控制的仿真结果作为对照组进行分析。作动器故障因子的取值情况如下。

表1 1/4车辆悬架主要参数

表 2主动悬架加速度输出表

故障1：故障因子σ=1，作动器无故障；故障2：在t=4 s时，取故障因子σ=0.2，作动器之后产生0.2倍的恒增益故障。

3.1 随机路面仿真

本文选取B级路面模型作为路面激励，其时域表达式为：

式中：v为车速，取v=10 m/s；q(t)为路面不平度位移的数值，单位m；n1为空间截止频率，取n1=0.01；n0为标准空间频率,取n0=0.1；w(t)为系统噪声，选用高斯白噪声；Gq(n0)为路面不平度系数,取Gq(n0)=6.4×10-5m3。

图3为故障1时的滑模控制与自适应容错滑模控制跟踪，理想天棚参考模型的簧上位移响应曲线。由图3可知，在作动器无故障时，两种控制算法都能对理想天棚参考模型簧上位移实现较好的跟踪。

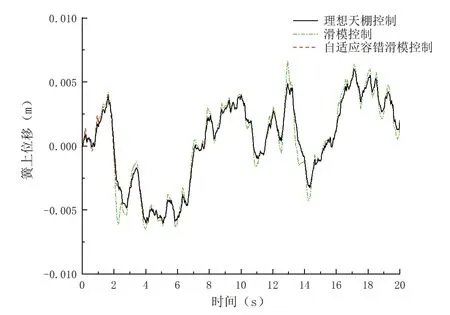
图3 故障1时的簧上位移响应曲线

图4 为故障2时两种控制器跟踪的簧上位移响应曲线。由图4 可知，在作动器故障发生后滑模控制器跟踪的簧上位移数值抖动剧烈，跟踪理想天棚参考模型效果较差；而自适应容错滑模控制器经过约2.5s后恢复至无故障时的跟踪效果，体现了较好的鲁棒性。

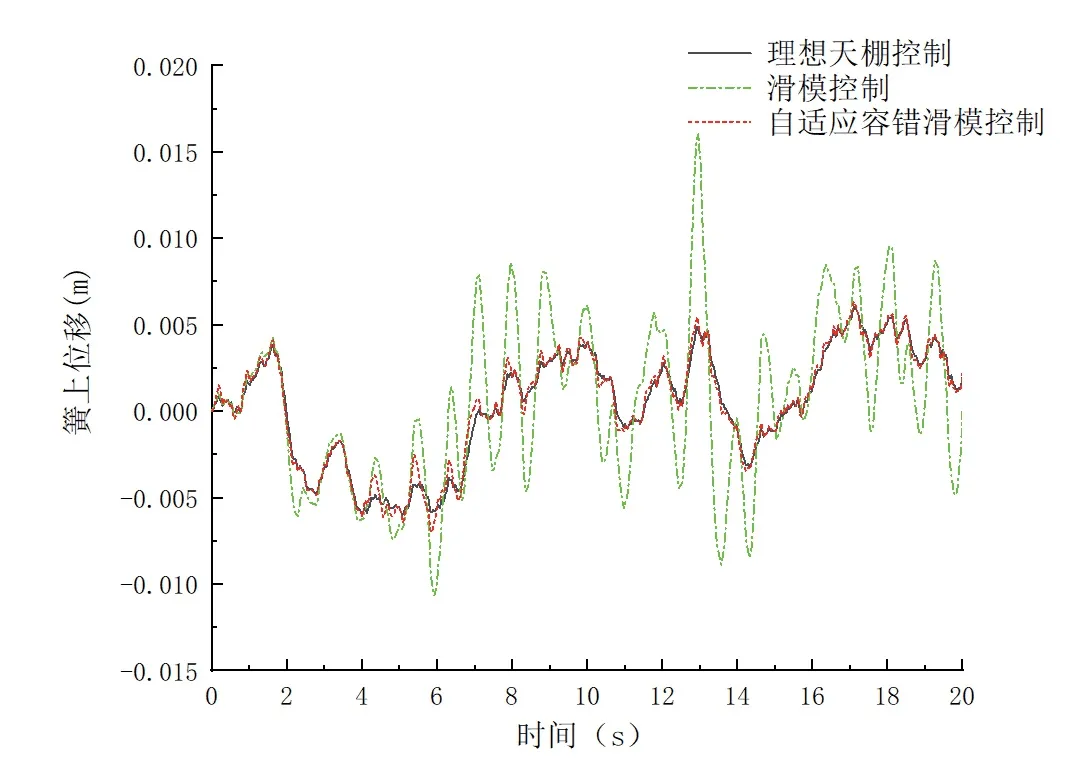
图4 故障2时的簧上位移响应曲线

图5为故障1时的车身垂向加速度响应曲线。由图5可知，两种控制算法控制下主动悬架车身垂向加速度响应曲线接近，因而在作动器无故障时两种控制算法控制效果大致相同。

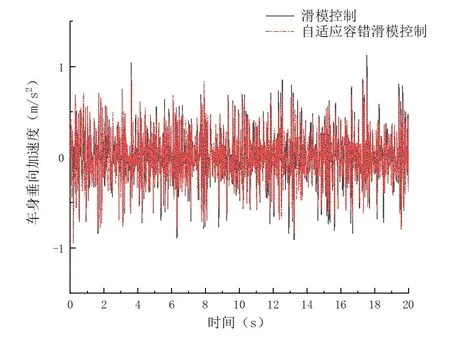
图5 故障1时的车身垂向加速度响应曲线

图6为故障2时的车身垂向加速度响应曲线。从图5中可以看出，在4s后作动器出现故障。相较于传统滑模控制，配置有自适应滑模容错控制器的主动悬架车身垂向加速度响应曲线幅值更小，鲁棒性能更好，提高了悬架系统的控制可靠性。

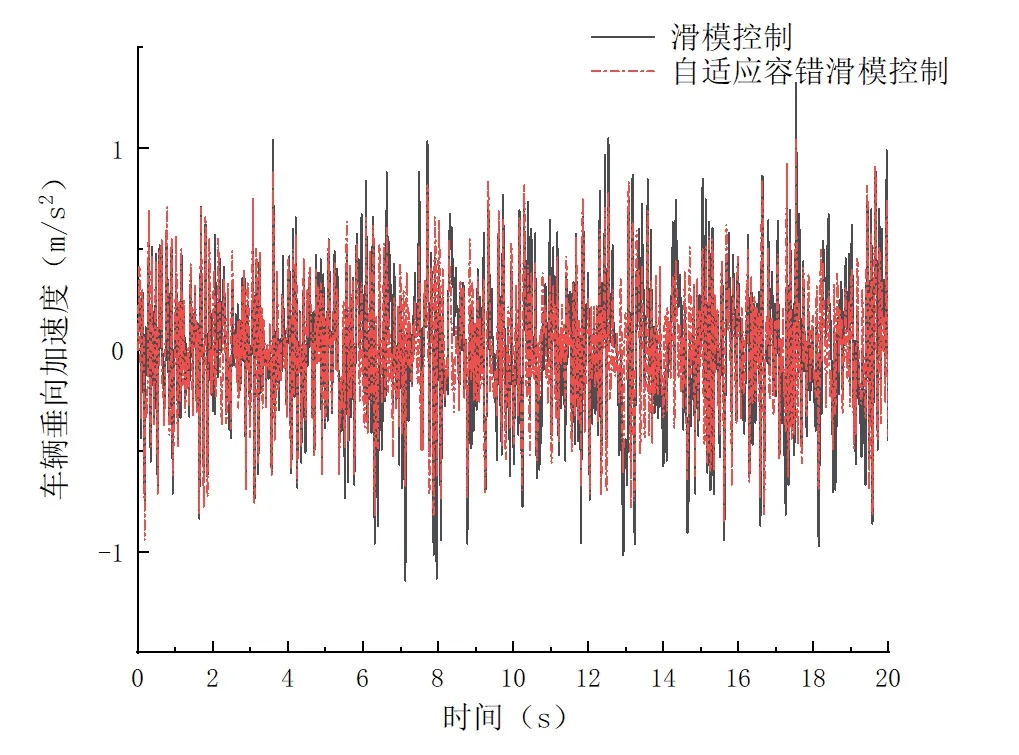
图6 故障2时的车身垂向加速度响应曲线

故障1与故障2情况下，主动悬架车身垂向加速度均方根值如表2所示。在故障1时，作动器无故障，两种控制算法控制下车辆垂向加速度均方根值相同；在故障2时，作动器发生故障时，配置有自适应容错滑模控制器的主动悬架相较于传统滑模控制，其车身垂向加速度均方值降低了11.1%，很好地改善了车辆乘坐舒适性，悬架系统鲁棒性能更好，验证了其容错性能的有效性。

4 结束语

本文以1/4主动悬架模型作为研究对象，针对主动悬架作动器故障对主动悬架系统控制可靠性的影响，设计了一种自适应容错滑模控制器，使主动悬架系统对作动器故障不敏感，提高了主动悬架系统的鲁棒性能。为了对所设计的控制器的有效性进行验证，在Simulink 中搭建了1/4主动悬架系统仿真模型，选取B级仿真路面激励进行了仿真验证。仿真研究结果表明，在作动器无故障时，所设计的控制器与跟踪理想天棚控制的滑模控制器控制效果大致相同。但在作动器发生故障后，对比传统滑模控制算法，所提出的自适应容错滑模控制器的鲁棒性能更好，有效地改善了车辆的乘坐舒适性和主动悬架系统的控制可靠性。