水轮发电机组机械故障的电气信号特征分析

顾 寅

（安徽省蚌埠闸工程管理处，安徽 蚌埠 233000）

转子失衡是转子系统中较为普遍的一类振动故障，传统的故障诊断方法通常采用振量值作为信号源，但其影响因素多，且不同测量点的幅值、幅值差异很大，致使分析结果可信度低，容易出现误判，而用电量作为信号源，则能很好地解决上述问题。

1 水轮发电机组转子振动故障原因分析

在水电站运行全过程中，其所监控的各类信号包含着机组运行状态的多种信息。如果单元出现故障，它所监控的信号也将发生改变。在此基础上，对发电机转子典型振动故障的产生机制进行了研究，并对故障产生的原因进行了分析，得到了相应的故障特征。通过深入研究转子振动故障的本质，能够更清晰地把握其发生及发展的整个过程，进而构建出更为合理的故障模型，为后续的理论研究与试验验证奠定理论基础。水轮发电机转子不平衡是转子振动故障中最常见的一种，现有的故障诊断信号来源多为振量值，因此，若将其作为信号源，能否实现。

1.1 电磁干扰引起的振动

发电机匝间短路是一种较为普遍的故障类型[1]。这直接关系到电动机的安全运行。定子线圈短时匝间短路，虽然不会对电动机的正常运转产生很小的影响，但是由于其特性并不明显，故在生产实践中往往被忽略。但是，长时间运行后，匝间短路可能导致转子绕组的一、二点接地。这种情况下，电机的大轴容易烧坏，转子的振动很大，而且转子容易被磁化。转子匝间短路时，气隙磁场会发生畸变，并联支路之间会出现高次谐波，严重影响发电机的正常运行，这会使绕组发热增大，进而影响到发电机的无功功率，造成机组振动，增加轴压，烧坏转子护环，最终导致筘座和大轮轴产生磁场，造成轴承瓦及大轴烧坏的严重事故。因此，准确地判定绕组中是否出现了匝间短路，并采取相应的措施，对解决这一问题具有一定的实际意义[2]。

转子在电磁谐振作用下，其振动幅度随有功、励磁电流增大或减小，且对负载变化十分敏感。但在额定速度下，激磁电流的增加或减少对振动的影响不大。在实际应用中，当发现谐振元件出现时，只能通过改变其结构，增大或减小其结构刚度，以避免其三阶谐波成分的影响。

1.2 机械原因引起的振动

若发电机转子的轴心位置与转轴有偏差，转子在离心力的影响下会发生受迫振动，称为不平衡。当转子中心位置的惯性主轴偏离转轴时，由于离心力的作用，转子会发生受迫的振动，也就是质量的不均衡[3]。转子失衡是发电机最常见的一种振动故障，其原因主要有：其发生率超过80%。近年来，国内外大型发电机制造厂对发电机转子的加工和装配精度以及电站设备的维修水平的不断提高，转子不均衡故障的数量在逐年下降。现在所有的电机厂都已经能在生产前对发电机转子进行快速均衡，一些发电厂也开始淘汰旧的动平衡机，改用更先进的移动动平衡机。即使这样，由于质量失衡而导致的机组振动依然是机组最大的问题。由于转子不平衡引起的转子振动的幅值及方向已有明确的规定，在实际应用中可采用动平衡的方法加以消除。除了质量不均衡外，还存在转子的热弯曲、转子内部存在可移动构件引起的不均衡等问题，这些非均衡的幅值和方向具有一定的可变性，在实际应用中很难用均衡方法加以消除。此外，由于机组密封片磨损过大，转子绕组出现了热膨胀，从而导致了转子的机械振动。

2 水轮发电机转子振动故障的电气信号特征分析

2.1 垂直振动量故障诊断有效性分析

让电机在50Hz 的情况下无负荷运转到额定工作状态[4]。然后，向平衡环施加42g 的失衡质量，对电动机的无负载电压进行测定，并对它进行快速傅里叶转换（FFT）分解。加工结束后，按相同程序添加不对称重量80g 和118g，测试空载电压，用FFT 分解。分析了负荷不对称对系统无功功率和频率的影响。研究发现，当转子频率为50Hz 时，在不添加不平衡量（零质量）的情况下，垂向幅值为0.02V；当不均衡重量42g 时，垂向幅度为0.05V；在不均衡重量80g 的情况下，垂向幅度为0.07V；当不平衡重量118g 被添加时，垂直幅度是0.10V。由此可以看出，当不对称质量增大时，电动机在空载时竖向振动量也随之增大。并对4 种非对称质量在25Hz、50Hz 情况下的垂向幅度进行了验证。

由图1 可以看出，在不添加不平衡量的情况下，电动机在不同频率下的竖向振动量是一致的。当频率为25Hz 时，纵向振动振幅随不平衡质量的增加而增加。在118g 不平衡量的情况下，马达在50Hz 频率下的竖直幅度是0.10V，25Hz 频率下的竖直幅度为0.14V。研究发现，当不平衡质量较大时，其自振频率较小，垂向振动较大，因此，利用竖向振量进行设备故障诊断具有可行性。

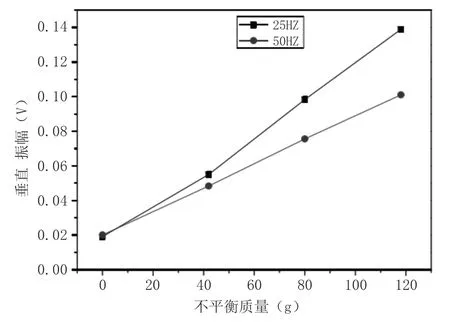
图1 垂直信号振幅随不平衡质量变化的特征曲线

2.2 水平振动量故障诊断有效性分析

机械发生故障时，除了垂直不正常的振动外，还会有水平方向的异常振动。测量横向振动量，以确保试验结果的准确性，其测试方法和上述一样，不再重复。测试结果显示，不加入不平衡度（不平衡度是0），当电动机的空载转矩为50Hz 时，其水平幅度为0.03V；当42g 的非均衡质量被添加后，其水平幅度是0.07V；添加80g 非均衡质量后，其横向幅度为0.11V；当添加118g 的非均衡质量时，其水平幅度为0.14V。从以上数据的变化规律可以看出，在50Hz 特性频率下，由于不对称质量的增多，其横向振动也随之加剧。在此基础上，对4 种不同的不平衡质量在25Hz 特征频段上的水平振幅进行了对比分析，得到了与实测数据一致的结果，结果如图2 所示[5]。

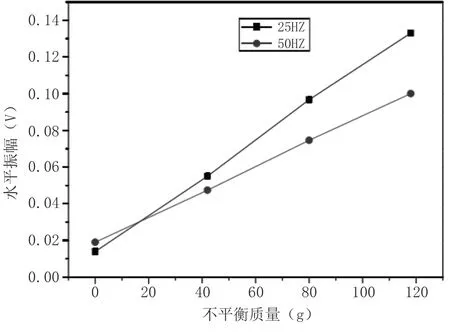
图2 水平信号振幅随不平衡质量变化的特征曲线

由图2 可知，当没有附加不平衡量的情况下，当电动机的转矩为50Hz 的时候，它的横向幅度比25Hz 时的小。然而，当不平衡量的质量越来越多时，在25Hz 左右的空载情况下，电动机的横向幅值就会迅速增大，并且在20g 不平衡量的情况下，其转矩已经超过了50Hz。当不平衡量最大（118 克）时，在50Hz 旋转频率下，空载运转马达的横向幅度为0.10V；而频率为25Hz 的电动机，其横向幅度只有0.14V。同时还表明，在高转速时，不对称质量越大，因此，用侧向振动量作为诊断发电机故障的方法具有一定的可行性。

2.3 空载电压电气量故障诊断有效性分析

通过对这两种类型的发电机的空载电压特性试验，证实了用振动量来诊断发电机的故障是可行的[6]。然后，进行发电机空载电压和电量测试，以实测电量特性为辅助，检查设备的机械故障。试验中，将电动机空载运转到额定工作状态，向平衡环中加入0g，42g，80g，118g 的不平衡量，并对其进行全谱分析。经过FFT 处理后，将振幅作为y 轴，不平衡量作为x 轴，得到同一频率下4 个不平衡质量的A 相振动幅度。例如，在没有添加不均质（不均质是0）的情况下，A 相的电压频率是100Hz，而电压幅度是0.48V；当添加42g 的不平衡质量时，得到0.53V 的电压幅度；在80g 的非平衡质量的情况下，电压幅度为0.55V；当添加118g的不平衡质量时，电压幅度是0.59V。从这些数据的变化规律可以看出，当电压和频率相等时，当不对称质量越大时，电压幅值越大。然后，用该方法测量了100Hz 时B、C 相电压幅值随4 种不均衡质量的变化，并将其横向比较，其结果显示在图3 中[7]。

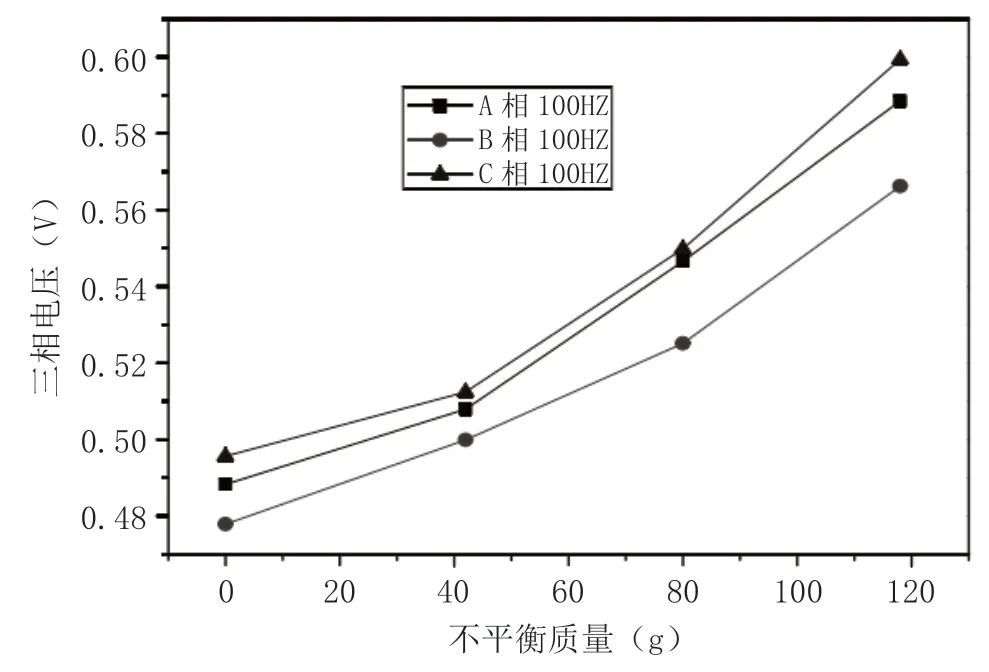
图3 不均衡质量改变时电压信号幅度的特性曲线

从图3 中我们可以得出以下两点：首先，100Hz 时，三相电压幅值随不对称品质的增大而呈同步变化；其次，当频率和不对称质量相等时，各个相的电压幅值存在一个规律，即C＞A＞B。同时，还说明了发电机空载电压和电量的谱特性可以用来判别机组的不对称故障[8]。

2.4 误差分析

为了排除随机误差，我们选择了三组的实验，剔除了有显著误差的实验数据。然后对剩余的数据求平均值，使实验结果的可信度得到很大的提高。此外，由于机组长时刻在非平衡状态下工作，很容易引发其它类型的故障，也有可能发生不均衡状态的叠加，因此，由测试得到的资料，仅能作定性的分析。本试验将发电机平放在地面上，并在发电机底部加装橡胶衬垫，以避免机组在工作过程中由于振动而发生偏移，但在实际试验中，仍发现发电机在非平衡状态下会出现较小的左右摇摆，从而造成测量结果的不稳定，因此所引起的试验误差并未计入试验结果。

2.5 不同频率下电气量频谱特征对比

理论分析认为，当不平衡质量为固定值时，当发电机发生不对称故障时，这种电机的无功功率具有二次频率特性，其大小与电机的参数有关。为检查在不同频率处多个非对称质量引起的电压幅值，用记号标出平衡环，将不同品质的不锈钢板依次放置。本文记录了82g 不均衡质量时的电功率频谱特征，见图4。

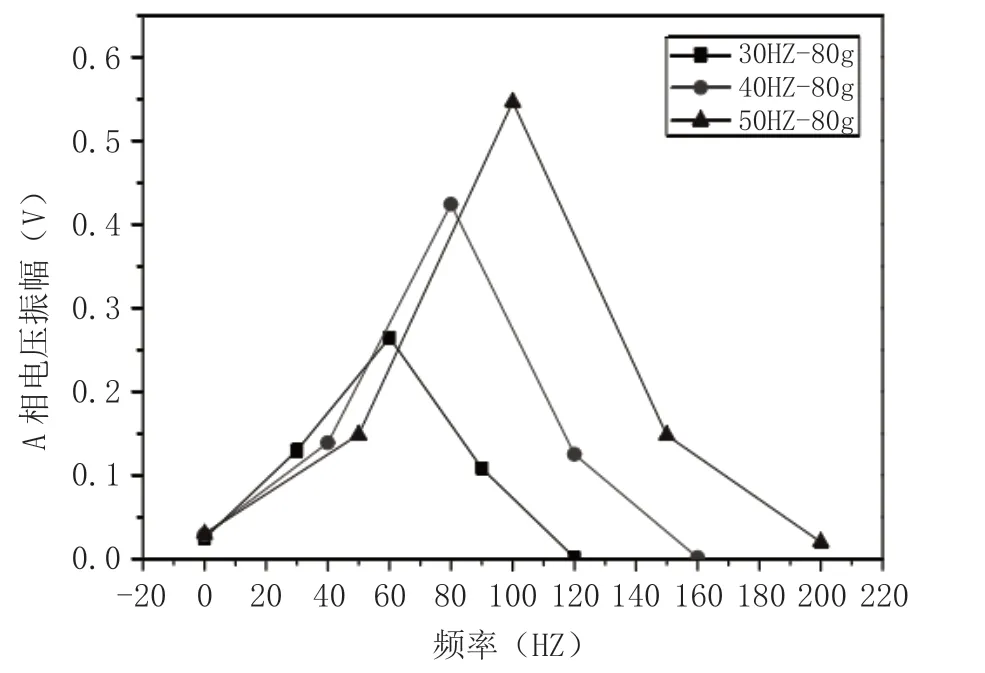
图4 82g 不平衡质量下的不同频率对比

3 结语

试验证明，利用振动幅值和通气量的谱特征能够识别出非对称的发电机转子不对称故障，这两个参数都随着非对称质量的增加而增加。结果表明：当电压频率恒定时，电压幅度随本征频率的升高而先增后减，该规律与本征频率为二倍、振幅与非对称成比例的理论推论相一致，为利用电气参数进行不平衡诊断提供了可能。