考虑双对数模型下非达西渗流的软土一维大应变固结分析

李兆帅,曹文贵,崔鹏陆,徐 赞,李慧鑫, 胡 闽

(湖南大学 土木工程学院,长沙 410082)

0 引 言

半对数模型曲线[1]是描述土体非线性压缩和渗透特性的曲线,同时它也是分析土体固结沉降最为经典的模型之一。但大量研究表明[2-3],对于发生较大应变的高压缩性软土而言,基于该模型描述的软土的非线性特性往往与试验结果存在较大的偏差。此外,土体固结还会受到非达西渗流[4-8]的影响。因此,建立同时考虑土体中的非达西渗流与大应变土体非线性压缩渗透模型来解决以上问题具有很重要的理论与实际意义。

近些年来,许多学者为寻求更适合描述大应变土体的非线性压缩渗透关系展开研究。Butterfieid[9]提出的双对数模型(lg(1+e)-lgσ′)(e为土颗粒孔隙比,σ′为有效应力),无论是对于发生小应变的软土还是大应变的软土,所展现出来的非线性压缩特性都能很好的与试验结果相契合。谢康和等[10]根据黏土非线性渗透特性试验总结出了软土指数形式的非线性渗透模型,弥补了土体发生较大应变时,经典半对数曲线不能很好描述软土非线性渗透特性的缺陷。李传勋等[11]则基于Butterfieid[9]、谢康和等[10]等提出的非线性压缩与渗透模型对高压缩性软土的一维非线性固结进行了分析,详细讨论了影响土体固结过程的因素,但其并未考虑非达西渗流对土体固结过程的影响。

事实上,在软土地基中,土体中渗流多属于非达西渗流。已有很多试验与研究表明软土中的渗流会偏离达西定律[4-8]。目前,考虑非达西渗流的软土一维非线性固结也已取得诸多进展。Zong等[12]在Slepickaf[6]提出的幂指数渗流模型基础上,修正了饱和黏土的一维固结理论, 并获得其有限差分数值解。李传勋等[13-15]基于Mesir等[1]提出的半对数关系引入非达西渗流,综合考虑了荷载作用、软土的结构性以及应力历史对土体固结的影响。但以上研究均在经典半对数关系,即e-lgσ′与e-lgkv(kv为土体渗透系数)关系的基础上展开的,对于发生大应变的软土不具有更广泛的适用性。

综上所述,本文在Butterfieid[9]、谢康和等[10]提出的lg(1+e)-lgσ′一维非线性压缩模型和lg(1+e)-lgkv渗透模型基础上,考虑非达西渗流对软土固结的影响,推导出了高压缩性软土的一维非线性大应变固结方程,并通过有限差分法对其求解。随后与解析解和试验数据进行对比,验证了本文解答的正确性,之后重点分析了不同土体参数对土体固结过程的影响。

1 固结方程的建立

地基固结模型简图如图1所示,H为软土层厚度,a表示软土层的竖向深度,顶面完全透水,底面完全不透水,并在初始有效应力σ′0作用下已完全固结,为简化地基沉降计算,不考虑饱和软土的流变特性。

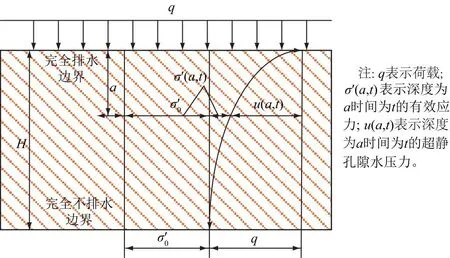
图1 地基固结模型

Butterfieid[9]、谢康和等[10]提出的非线性压缩模型和非线性渗透模型如下:

(1)

(2)

式中:e0为与初始有效应力σ′0相对应的孔隙比;kv、kv0分别为土体的渗透系数和初始渗透系数;Ic、Ik分别为双对数坐标系中土体的压缩指数和渗透指数,其中Ik=1/α,α为渗透模型参数。

根据土体体积压缩系数定义[16],由式(1)可得

(3)

由式(1)、式(2)可求得渗透系数表达式,即

(4)

基于非牛顿指数描述的非达西渗流表达式为[5]

(5)

式中:v为渗流速度;i为水力梯度;kv为渗透系数;i0为非牛顿指数,其物理意义为v-i曲线渐近线的截距。

大应变假定下一维固结的普遍连续方程为[16]

(6)

式(6)可进一步改写为

(7)

大应变假定下的水力坡降表达式为[16-17]

(8)

式中:e0为土体初始孔隙比;e为孔隙比;γw为水的重度;u为超静孔隙水压力。

根据有效应力原理,土的有效应力σ′为

σ′=σ′0+qu-u。

(9)

式中qu为加载荷载大小。

结合式(3)—式(5)、式(8)、式(9)代入式(7)可得考虑双对数模型与非达西渗流的软土一维大应变固结方程:

(10)

(11)

(12)

控制方程的求解条件表达为

(13)

2 固结方程的差分求解

引入如下无量纲参数:

将无量纲参数代入控制方程式(10)及求解条件式(13)中得

(14)

其中:

A=(S+Q-U)Ic+1;

(15)

B=(S+Q-U)-Icα;

(16)

C=(S+Q-U)Ic;

(17)

(18)

控制方程的求解条件应用无量纲变量表达为

(19)

本文的软土一维大应变固结方程式(14)很难求出其解析解,因此采用有限差分法对该固结方程进行求解。在Z-Tv平面划分差分网格,i和j分别表示空间节点和时间节点,i=0,1,2,…,n;j=0,1,2,…,k。i=0和i=n分别表示软土层顶部(a=0)和底部的位置(a=H),j=0和j=n表示初始时刻(Tv=0)和最终时刻。ΔZ表示空间步长,ΔTv表示时间步长,将式(14)差分可得

(20)

进一步整理化简可得

其中:

(22)

(24)

(25)

此时可进一步求得按孔压定义的平均固结度Upt如下

(26)

Tv时刻土层发生的沉降St为

(27)

可以得到

(28)

土层发生的最终沉降量S∞为

H{1-[(σ′0+qu)/σ′0]-Ic} 。

(29)

同理可求得按变形定义的平均固结度Ust为

Ust=St/S∞。

(30)

3 解答验证

为验证本文有限差分解法的正确性以及在工程上的可行性,将本文数值解与相关解析解和试验数据对比。

3.1 与解析解对比

通过与李传勋等[11]提出的解析解与本文利用差分法所得的数据进行对比,以验证本文差分数据的正确性。

李传勋等[11]基于达西渗流下将软土非线性大应变固结解析解分3种情况展开求解,因此需将非牛顿指数渗流退化为达西渗流(i0=0),并采用表1中给出的土体参数作为计算参数取值。

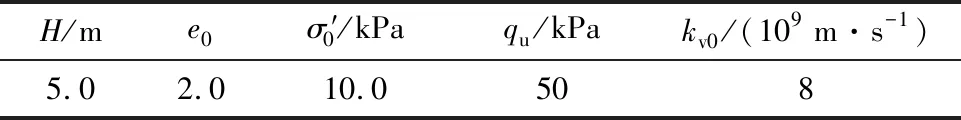
表1 文献[11]中的土体参数

为开展3种求解情况下对比分析,参数Ic与α取值如下:①为满足Ic(α-2)=1的情况,Ic=0.118,α=10.475;②为满足Ic(α-2)≠1且Ic(α-1)≠1的情况,Ic=0.095,α=11.5;③为满足Ic(α-1)=1的情况,Ic=0.125,α=9.0。将3种情况下Ic与α值代入公式,得到超静孔压随深度变化曲线和沉降随时间变化曲线,并与李传勋等[11]论文解析解对比,结果如图2和图3所示。从图中可以看出,取相同参数时,解析解与本文有限差分法所得出的数据完全吻合,从而验证了本文有限差分法的正确性。

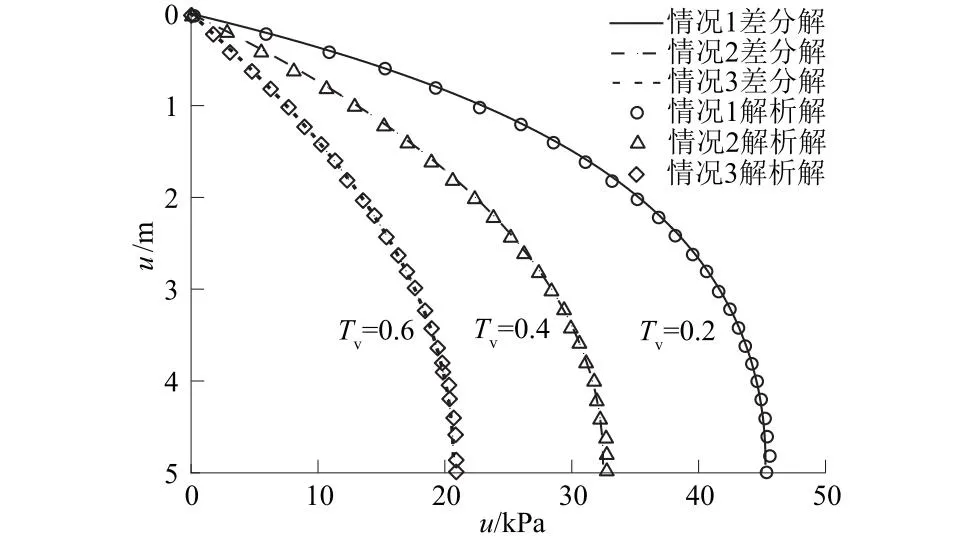
图2 3种情况下超静孔压的差分解与解析解对比

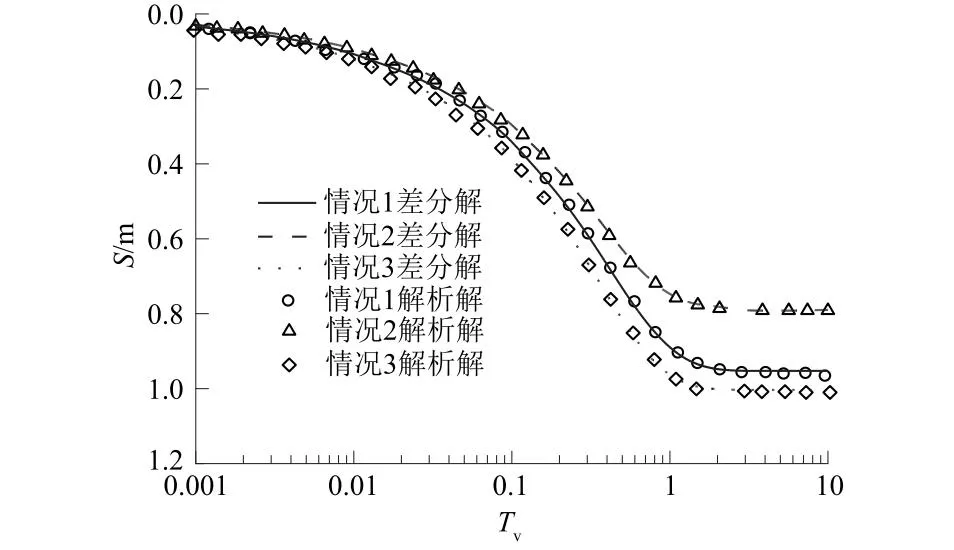
图3 本文解与李传勋解的沉降对比

3.2 与室内试验对比

为进一步验证本文所利用的有限差分解法的可行性,将本文理论计算得到数值解与张明[18]在试验中测得的数据进行对比。为保持跟室内试验一致,同样将非牛顿指数渗流退化为达西渗流(i0=0),在进行程序计算时参数选取也与室内试验土样数据一致。计算所采用的土工参数如表2所示。

表2 张明[18]试验的土体参数

室内试验的土壤样品为取自深圳前湾地区的吹填淤泥土,经过初步检测,该土壤样品的含水量与天然密度分别为109.42%和1.41 g/cm3,土颗粒的查对密度和初始孔隙比分别为2.68和2.98。张明[18]基于GDSCTS固结仪对吹填淤泥土进行固结渗透室内试验。试验排水条件为单面排水,加载方式为25 kPa至50 kPa的分级施加,每级加载均可视为前一级荷载稳定后的瞬时加载。计算土样在荷载qu=25 kPa下的沉降随时间变化曲线,其与室内试验得到的沉降曲线对比如图4所示。从图4可以看出,采用有限差分法在qu=25 kPa加载情况下计算出的数值解与室内试验实测的沉降值基本吻合,但通过试验实测的沉降值要略微小于采用有限差分方法计算得到的理论值。其原因可归结于在本文的地基固结模型假定中,上排水界面是完全渗水的,而下排水界面则是完全封闭的,但是在进行室内试验时因存在不可避免的系统误差等从而导致其上层和下层的排水条件并不能达到理论假定中的理想情况。尽管理论计算出的数值与试验结果上存在一定的差异,但是它的沉降变形随时间的变化趋势也表明了该方法在工程上应用的可行性。

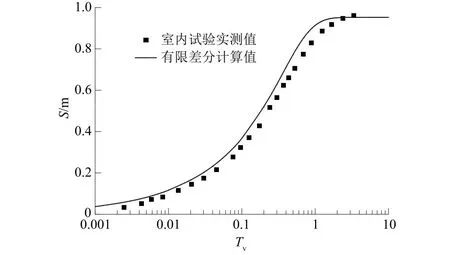
图4 差分解与试验实测的沉降与时间关系曲线对比

4 参数分析

基于以上验证结果的正确性,现以顶面透水及底面不透水地基模型为例,分析非达西参数i0、压缩指数Ic和渗透模型参数α以及荷载qu对土体固结过程的影响,所需计算参数如表1所示。

4.1 非牛顿指数i0对固结性状的影响

刘忠玉等[19]研究表明,与达西渗流相比,非达西渗流会对土体的固结有明显的滞后效应。而这种滞后效应与非牛顿指数i0有关。如图5所示,与达西渗流(i0= 0)相比,非牛顿指数渗流情况下底部超静孔隙水压力消散较慢,且其消散速度随i0的增大而减小;从图6可以看出与达西渗流(i0= 0)相比,非牛顿指数i0并不会改变软土层最终的沉降量,但却会影响达到最终沉降的时间,i0越大,其达到最终沉降值所需要的时间越长,在同一时刻土层的沉降就越小,该结论与刘忠玉等[19]的观点一致。

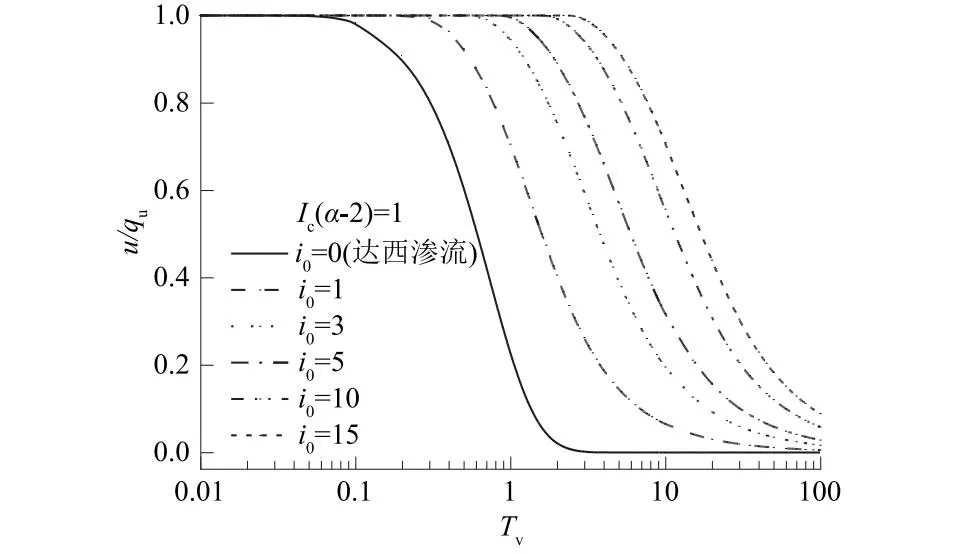
图5 不同 i0下底层超静孔隙水压力u关于Tv的关系曲线

图7描述了非牛顿指数i0对平均固结度Ust的影响,其随时间TV的变化趋势与李传勋论文一致。随着非牛顿指数i0的增大,非达西渗流情况下的Ust曲线会越加偏离达西渗流情况下的Ust曲线,具体表现为非牛顿指数i0越大,土体中超静孔隙水压力消散越慢,土体沉降速率越慢,其达到最终沉降所需的时间越长。同理Ic(α-2)≠1且Ic(α-1)≠1,Ic(α-1)=1这两种情况下规律与Ic(α-2)=1情况下类似,就不多做陈述。

图7 i0对平均固结度Ust的影响

4.2 参数Ic与α对固结性状的影响

采用表1中的土体参数,固定非达西参数i0=3.0,qu取值100 kPa,分别在Ic=0.1,α=9、12、15和α=12,Ic=0.075、0.1、0.125时讨论其对固结性状的影响。仇超等[20]的研究中表明,压缩指数Ic与渗透模型参数α都会影响到土的固结过程。图8为Ust与Upt随时间因子Tv的关系曲线。由图8可知,Ic=0.1时,平均固结度Ust(按变形定义)和平均固结度Upt(按孔压定义)都会随α的增大而减小,这表明α越大,渗透指数越小,软土的渗透性越弱,固结速率越慢;同理,在α=12时,Ust与Upt会随压缩指数Ic的增大而减小;图9为Ust与Upt的对比曲线,可发现在同一时刻下Ust要快于Upt,这表明土层变形的发展快于孔压的消散,该结论与谢康和等[21]阐述的观点一致。

图8 Ic和α对 Ust与 Upt的影响

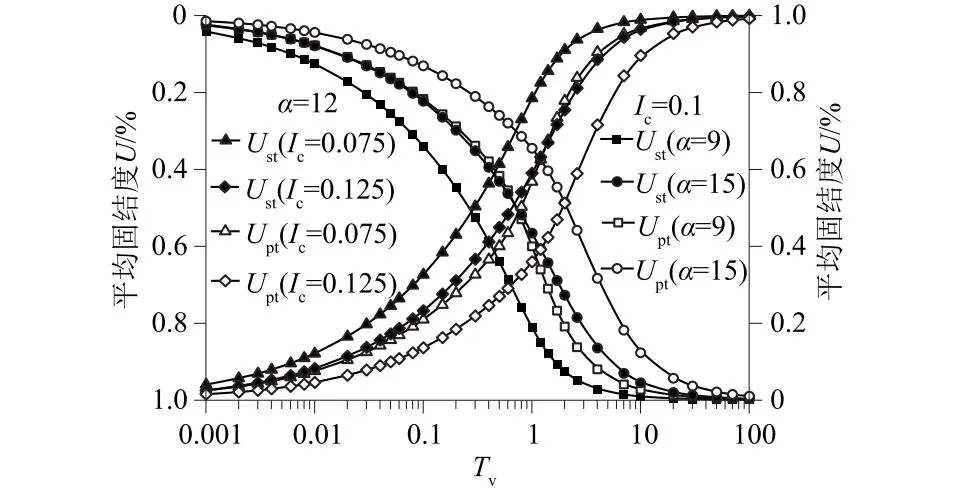
图9 不同 Ic和α下平均固结度与 Tv关系曲线

图10描述了Ic和α对底部超静孔隙水压力的影响。由图10可知,在同一时刻,α越大,薄土层底部超静孔隙水压力越大,这表明土层的渗透性越差,底部超静孔隙水压力消散越慢。同理,Ic越大,在同一时刻薄土层底部超静孔隙水压力越大,这表明土层的压缩模量越小,底部超静孔隙水压力消散越慢,固结的速率也就越慢。

图10 Ic和α对底部超静孔隙水压力的影响

4.3 外荷载qu对固结性状的影响

采用表1中的土体参数,固定非达西参数i0=3.0,参考前文非牛顿指数i0对固结性状的影响分析。图11表明,随着荷载qu的增大,土层的沉降就越大,土层中超静孔隙水压力消散越快。这表明荷载越大,孔隙水压消散速度越快,孔隙比减小量越大,故按孔压定义的平均固结度与按变形定义的平均固结度也就越大。此规律与刘忠玉等[19]的结论相一致,这也是达西定律下的太沙基一维固结理论所不能预测的。

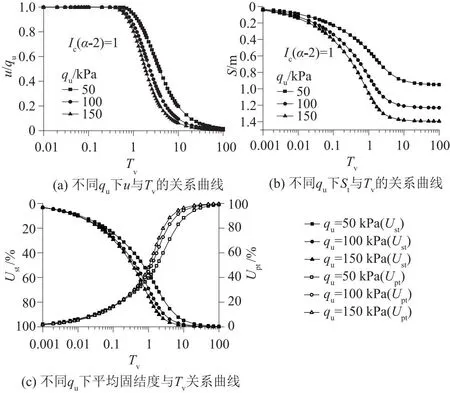
图11 外荷载qu对固结性状的影响

5 大小应变差分解对比分析

本章参考李传勋等[11]仅改变土体一维非线性固结几何假定而保证其他假定不变的做法,分析在双对数非线性关系下分别应用大小应变固结理论进行计算的差异。引用Pu等[22]算例进行分析:H=2 m,σ′0=1 kPa,e0=4.3,Ic=0.097,α=7.89。不同荷载取值见表3。

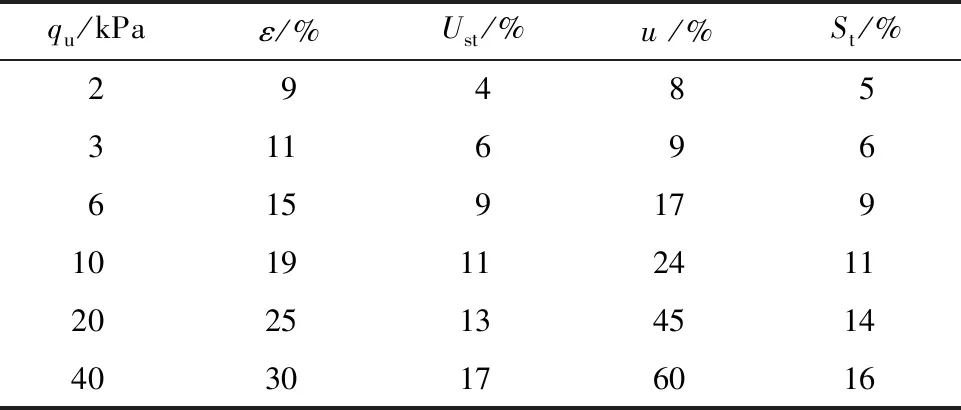
表3 大小应变下固结性状最大相对偏差

由图12和表3可知:当土体发生较小应变(ε<15%)[23-24]时,虽然在非牛顿指数渗流下大应变固结理论得到的土体固结速率要略快于小应变假定下的固结速率,但两者理论假定下计算得出反映其固结性状的各曲线都较为接近;但当土体发生较大的应变(ε≥15%)时,两者固结曲线就会出现较为的差异,且此差异会随着应变值的增大而不断扩大。由表3可以具体看出,当应变值为19%时,大小应变假定下计算的超静孔隙水压力最大偏差为24%,沉降的最大偏差为11%;而当应变值增大到25%时,超静孔隙水压力最大偏差为45%,沉降的最大偏差为14%;当应变值达到30%时,超静孔隙水压与沉降的最大偏差更是增大到了60%与16%。此外图12(c)表明,虽然大小应变不同假定会影响土层固结速率的计算差异,但并不会影响到最终的沉降量。

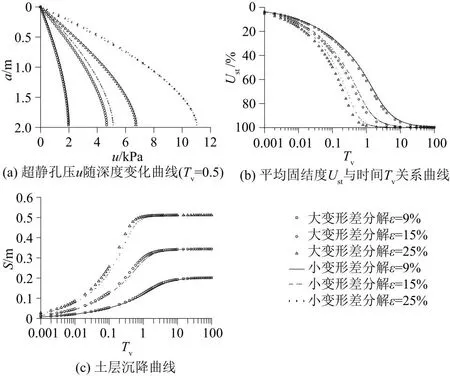
图12 大小应变差分解对比

因此可分析得出,当土层的应变较小(ε<15%)时,大小应变理论得出的数据差异并不大,此时采用小应变固结理论开展计算是可行的,但当土层的应变较大(ε≥15%)时,由于大小应变固结理论计算得到的数据存在较大的差异,在大应变固结理论下沉降固结速率较快。虽然大小应变不同假定下最终沉降值趋于一致,但是在未达到最终沉降的过程中,各时间节点下按大小应变计算得到的固结沉降曲线存在差异,对地基的沉降变形预测要求甚高的沿海地区的软土而言,固结沉降过程中的差异不容忽视。考虑实际工程不同于理论计算中的理想,工况也更加复杂,为安全起见建议采用大应变固结理论计算。

6 结 论

(1)土的非达西渗流对土的沉降过程有较大的影响,即非达西渗流参数i0越大,土中超静孔隙水压力消散越慢,土体固结速率越慢,达到最终沉降量所需的时间越长。

(2)Ic一定时,参数α越大,土层超静孔隙水压力消散速率和固结速率越慢;α一定时,参数Ic越大,土层超静孔隙水压力消散速率和固结速率越慢。这表明土体压缩模量越大、渗透性越好,土层底部静孔隙水压力消散速率和土层的固结速率越快。此外,在同一时刻下Ust要快于Upt,这表明土层变形的发展快于孔压的消散,故在实际工程中为安全起见建议采用Ust来预测土层的固结发展。

(3)外荷载qu越大,土层的沉降量就越大,底部超静孔隙水压力消散越快,土层的固结速率也越快。

(4)大、小应变固结性状的差异会随土层应变增大而不断扩大。当土层的应变较小时(ε<15%),两者的固结沉降与孔压曲线较为接近;当应变逐渐增大时,两者各曲线之间的差异被逐渐放大。因此当土层的应变较大时(ε≥15%),为安全起见建议采用大应变固结理论计算。此外,因几何假定不同,大应变固结理论计算的土层固结速率均快于小应变固结理论计算的固结速率,但两者并不会影响到最终的沉降量。