新型3PRPaR并联机器人的设计与多目标优化

张发海,李丽红,朱 磊

(1.江苏安全技术职业学院智能制造与应急装备学院, 江苏 徐州 221011)

(2.中国矿业大学材料与物理学院, 江苏 徐州 221116)

三平移并联机构具有操作空间大、动态性能好、制造成本低、无支链干涉等优点[1-2],广泛应用于装配、包装和食品加工等工业领域[3-4]。

近年来,越来越多的学者对这类机构进行了构型综合和结构优化。文献[5]设计了一种低耦合度三平移并联机构,根据单开链的奇异性分析方法得到奇异位形存在条件。文献[6]研究不同驱动类型的Delta并联机构,并建立刚度指标和综合灵巧度指标,研究结果表明,工作空间体积相同时,直线驱动型Delta并联机构相比转动驱动型Delta并联机构刚度性能更好,而转动驱动型Delta并联机构运动性能更为突出。文献[7]提出一种弱耦合2RRPaR+PPaP并联机器人机构。以上文献仅进行了工作空间性能的优化。文献[8]提出一种改进的Delta机构,通过性能对比分析表明改进的Delta机构运动性能较好。文献[9]研究一种具有较大操作空间、位置正解解析式、运动解耦特点的三平移并联机器人机构。文献[10]采用动平台支链的演化方法,提出一种末端铰接的空间三平移并联机构,并建立灵巧度和工作空间双目标优化模型,此文献仅考虑了灵巧度和工作空间的优化。

综上所述,目前大部分目标优化是单目标优化,多目标优化也仅涉及工作空间和灵巧度,而忽略了全域性能波动指标对机构运动的重要性。本文以三维移动并联机构为研究对象,研究了操作空间的形状和大小以及运动性能灵巧度、奇异性等特性。考虑全域性能波动指标对运动性能的影响,选择经典的NSGA-Ⅱ算法完成多目标参数优化,得到满足各项性能指标的Pareto解。

1 并联机构拓扑分析

1.1 机构结构设计

图1、2为3PRPaR并联机构结构简图、三维图,P表示移动副,R表示转动副,Pa表示由4个转动副互相平行且连接平行四边形机构。单开链结构为{(Pi)⊥(Ri1⊥P4R)⊥Ri2},i=1,2,3,其中Ri1∥Ri2。机构的主动副位移定义为(q1,q2,q3),移动副移动长度为L,平行四边形长边长为l1,动、静平台外接圆半径分别为r、R。

图1 3PRPaR并联机构结构简图

图2 3PRPaR并联机构三维图

1.2 方位特征集分析

动平台的运动输出特性可根据方位特征集理论计算得到[11]34-47,每条支链方位特征集(POC)Mbi为:

(1)

式中:t表示移动副,r表示转动。

机构的POC集Mpa(1-2-3)计算结果为:

(2)

1.3 自由度分析

自由度计算公式有很多,可参考文献[11]85-90方位特征集分析中的计算公式:

(3)

(4)

式中:F为自由度;m为机构运动副数;v为机构独立回路数目,v=m-n+1,其中n为机构运动副构件个数;fi为支链第i个运动副的自由度个数;ξLj为第j个回路的独立位移方程数;Mb(j+1)为第(j+1)条支链POC集。

1)分析第1条独立运动回路方程数,计算独立位移方程数ξL1:

(5)

2)分析第2条独立运动回路方程数ξL2:

(6)

式中:Mpa(1-2)为由支链1、2构成的方位特征集。

将独立位移方程数代入式(3)、(4)计算机构自由度F,得:

(7)

方位特征集分析以及自由度计算表明:经理论验证机构执行末端能够沿着空间x、y、z方向移动。

2 位置分析

2.1 位置逆解分析

在静平台A1A2A3中心O点建立静坐标系{O-xyz}。坐标原点O建立在外接圆的中心,其中x轴平行于直线A2A3,y轴经过OA1,z轴垂直于静平台平面。机构的运动学方程建立过程具体如下:

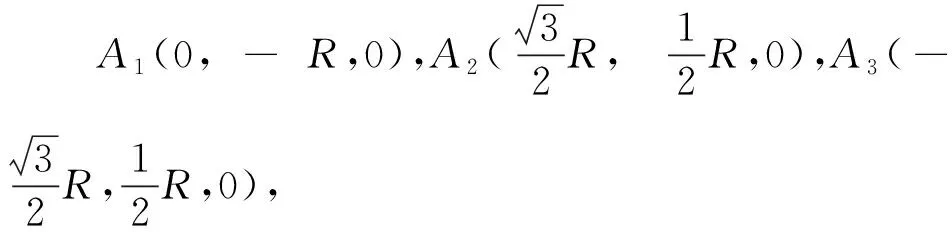
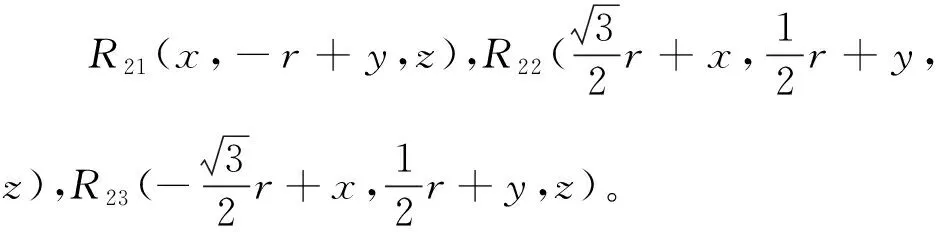
3)根据几何模型图(图3),可得:

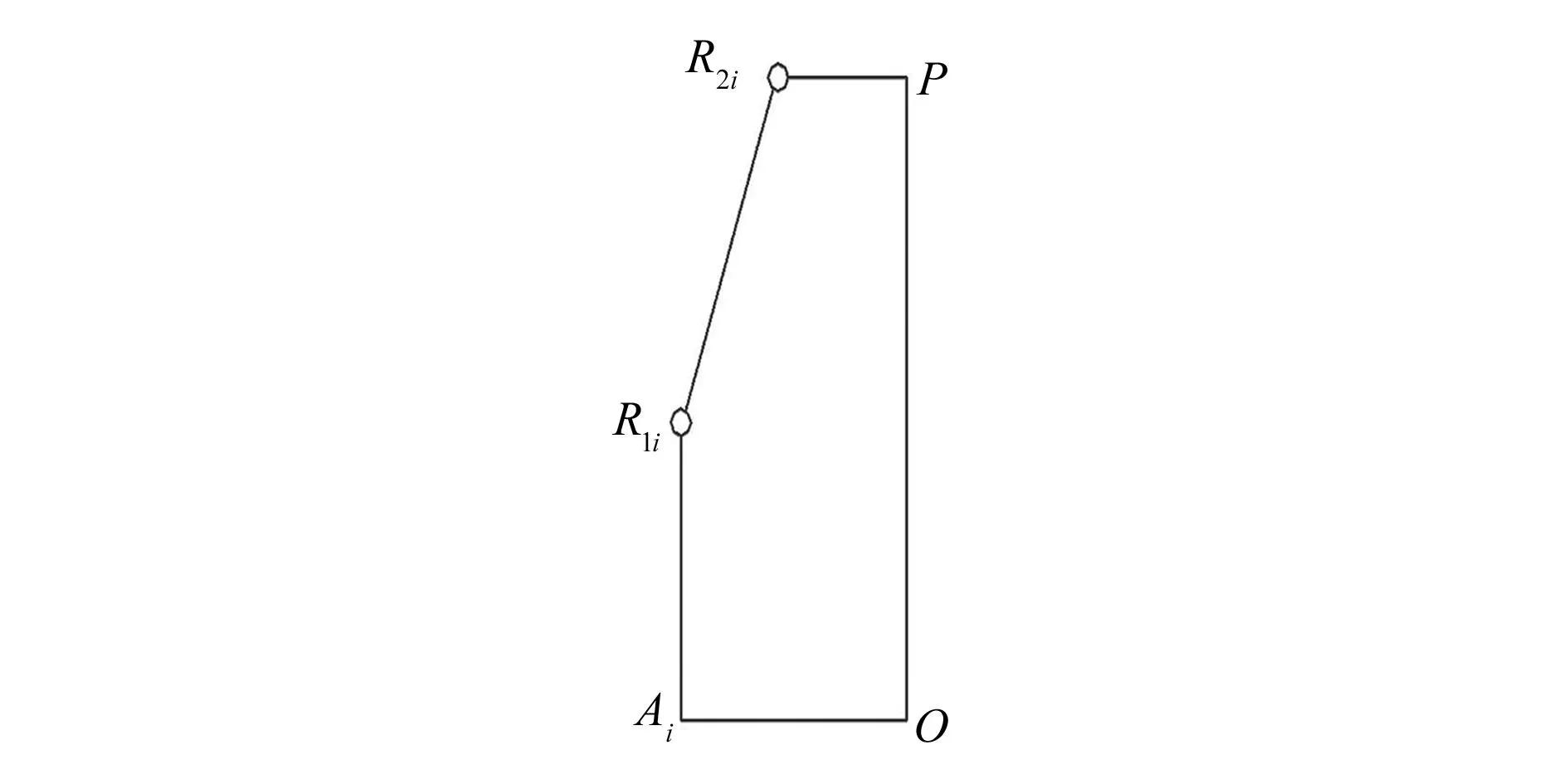
图3 几何模型图

R1iR2i=(OP+PR2i)-(OAi+AiR1i)

(8)

4)利用矢量法将R2i、R1i坐标点代入式(8)中,推导出机构运动方程模型:

(9)

将驱动副位移变量分离,得到逆解表达式:

(10)

2.2 驱动副运动性能仿真

设计平台的螺旋运动轨迹为:

(11)

式中:t为时间。

运动轨迹如图4(a)所示,参数取值为L=2 m、l1=0.8 m、r=1.2 m、R=1.5 m,通过机构仿真得到机构驱动副位移变化轨迹,如图4(b)所示。平台轨迹沿着等距螺旋线上升时,驱动副位移呈现不同相位的正弦上升趋势,具有连续和稳定的特点。

图4 螺旋运动轨迹和驱动副位移变化轨迹

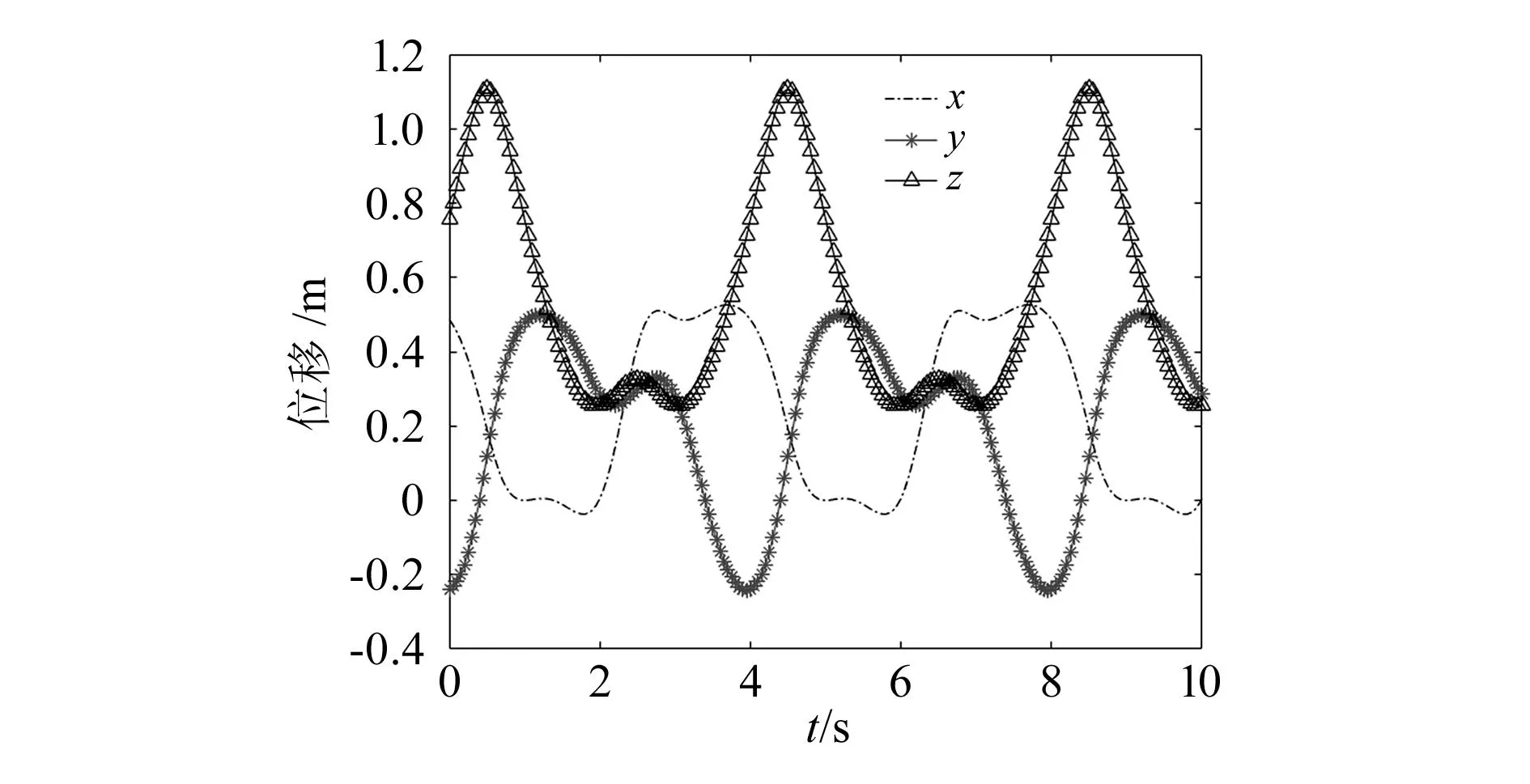
图5 动平台驱动轨迹

2.3 驱动副正解性能

采用2.2节的参数,未限定L值。

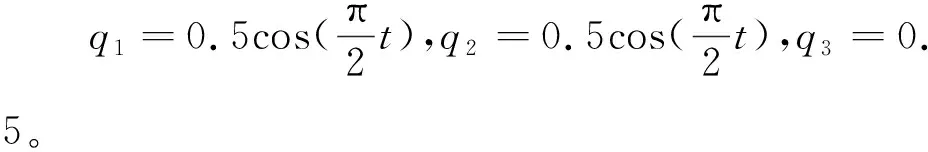
由此可以得到动平台在x、y、z轴方向上的驱动轨迹,如图 5 所示。可以发现动平台位置变化平稳,表明机构的传递性能优良,和2.2节中的分析结果一致。

3 奇异性分析

3.1 机构雅可比矩阵

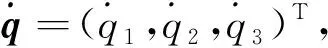
对式(9)分别求导和作分离变量处理,根据方程(12)计算得到逆雅可比矩阵Jx、正雅可比矩阵Jq。

(12)

(13)

3.2 逆解奇异性分析

机构逆解奇异条件为det(Jq)=0且det(JX)≠0。使得det(JX)=0的条件是:1)z=q1,支链1驱动副位移和动平台在同一高度。2)z=q2,支链2驱动副位移和动平台在同一高度。3)z=q3,支链3驱动副位移和动平台在同一高度。因此以上3种边界奇异应尽量避免。

3.3 正解奇异性分析

机构正解奇异条件为det(JX)=0且det(Jq)≠0。由det(JX)=0可得:

det(JX)=(q3-z)n3-(q2-z)n2-(q1-

z)n1=0

(14)

使得det(Jq)=0的条件是:1)q1=q2=q3=z,此时支链1、2、3的移动副的垂直高度和动平台高度末端完全一致。在这种情况下必然要求r+L=R,因此在设计机构时,可以控制r+L>R,这样就能完全远离这类奇异位形点。2)h=R-r=0,即动静平台的半径相同,此时平行四边形无法安装,为了避免这种奇异出现,应合理设置机构结构参数,使r+L>R。

4 机构的工作空间分析

工作空间是指机构执行末端的最大运动范围,可作为衡量机器人性能的评价指标[12]。基于数值法完成工作空间搜索,选择一组参数搜索工作空间边界,参数值分别为L=2 m、l1=0.8 m、r=1.2 m、R=1.5 m。

由图6可知:工作空间由3个相同的扇形构成,沿着xoy平面呈对称分布,边界光滑,无空洞分布情况。其三维图沿着xoz平面以及yoz平面的投影图形相同,都是半椭圆形。

图6 3PRPaR机构工作空间

5 并联机构运动灵巧性分析

灵巧度是评价并联机构运动灵活性的性能指标,本文以雅可比矩阵条件数倒数作为灵巧度指标,来分析机构运动过程中的灵巧性。仿真分析得到灵巧度性能图谱如图7所示。由图可知:机构在工作空间内的普遍不高,最大值为0.22,局部的灵巧度值为0,灵巧度分布不均匀。

图7 运动灵巧度分布

6 并联机构多目标优化

6.1 模型优化的建立

为了评价机构在整个可达工作空间内的运动灵巧性,行业内定义了衡量机构运动性能的全域性能指标,也称为全局灵巧度[13]。全域性能指标η仅能反映工作空间内运动性能的平均值,实际应用过程中,还要求运动性能稳定,不能波动太大,灵巧度在全域的分布更均匀。全域性能指标η和全域性能波动指标σ定义如下:

(15)

(16)

式中:w为可达工作空间体积,LCI为灵巧度。

工程应用中期望η和w尽可能大而σ尽可能小,现分别以全域性能指标F1、工作空间体积Vw和全域性能波动指标F2作为优化目标函数,多目标优化模型具体如下:

(17)

(18)

6.2 优化算法的选择

多目标优化采用经典的NSGA-Ⅱ优化算法,能够得到满足多目标的Pareto优化机构参数解集,通过机构参数解集获取实际需求参数值[14]。

优化曲面如图8所示。由图可知,全域性能指标和工作空间体积是背离的,当工作空间体积为5.8 m3时,全域性能指标和对应的全域性能波动指标均为0;当全域性能指标为0.20时,工作空间体积小,全域性能波动指标大。这表明同时获得较小的工作空间体积和较大的全域性能指标是不可能的,只能折中选取较为均衡的目标值。表1选取了6组Pareto优化参数,图9是相应参数下的灵巧度在空间的分布。

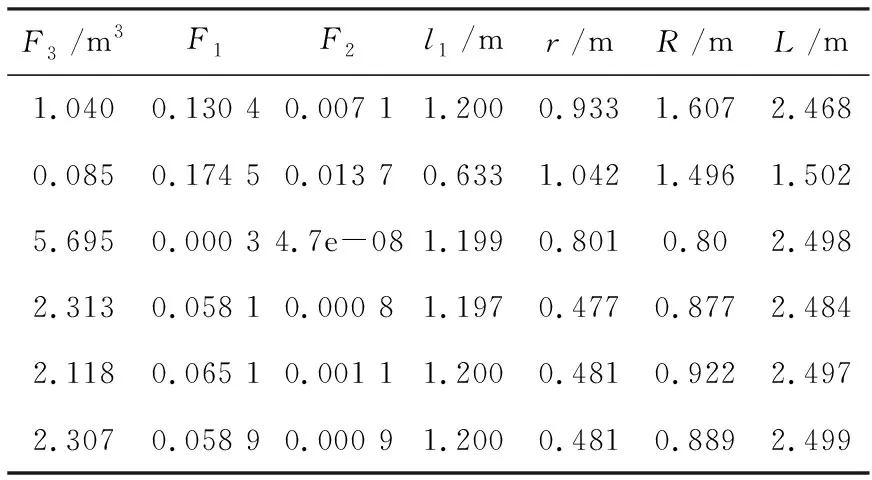
表1 并联机构优化前沿集的部分尺寸参数

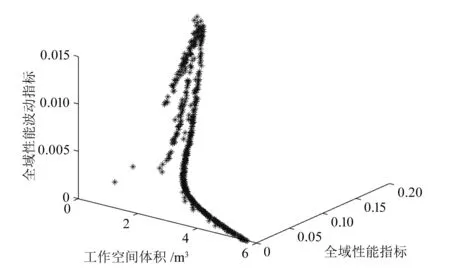
图8 Pareto前沿优化曲面

由图9可知,工作空间体积较小(第1组和第2组)时,其灵巧度沿y=0.2截面分为两部分,最大灵巧度靠近y=0.5和x=0的部分;工作空间体积较大(第3组～第6组)时,灵巧度被分割为4个区域,分割界面为y=±0.4、±0.5、±0.5和±1.0,分割面上的点存在奇异性且灵巧度为0;第3组和第6组的最大灵巧度和第1、2组相同。从实际应用出发,第3组参数虽工作空间较大,但灵巧度却很小,可不选取;第1组参数和第4、5、6组参数可以考虑使用,它们平衡了工作空间体积和灵巧度,其中第4组的全域性能波动指标值最低,因此第4组可作为较为理想的设计参数值。

6.3 优化后仿真验证

选择一组优化后的参数对并联机构三维建模,同时对其进行抓取工件的动态运动仿真,图10为机构抓取工件过程中的不同位置。由图可知,运动过程无跳变情况,运动平稳。仿真结果表明,机构的运动性能较好。

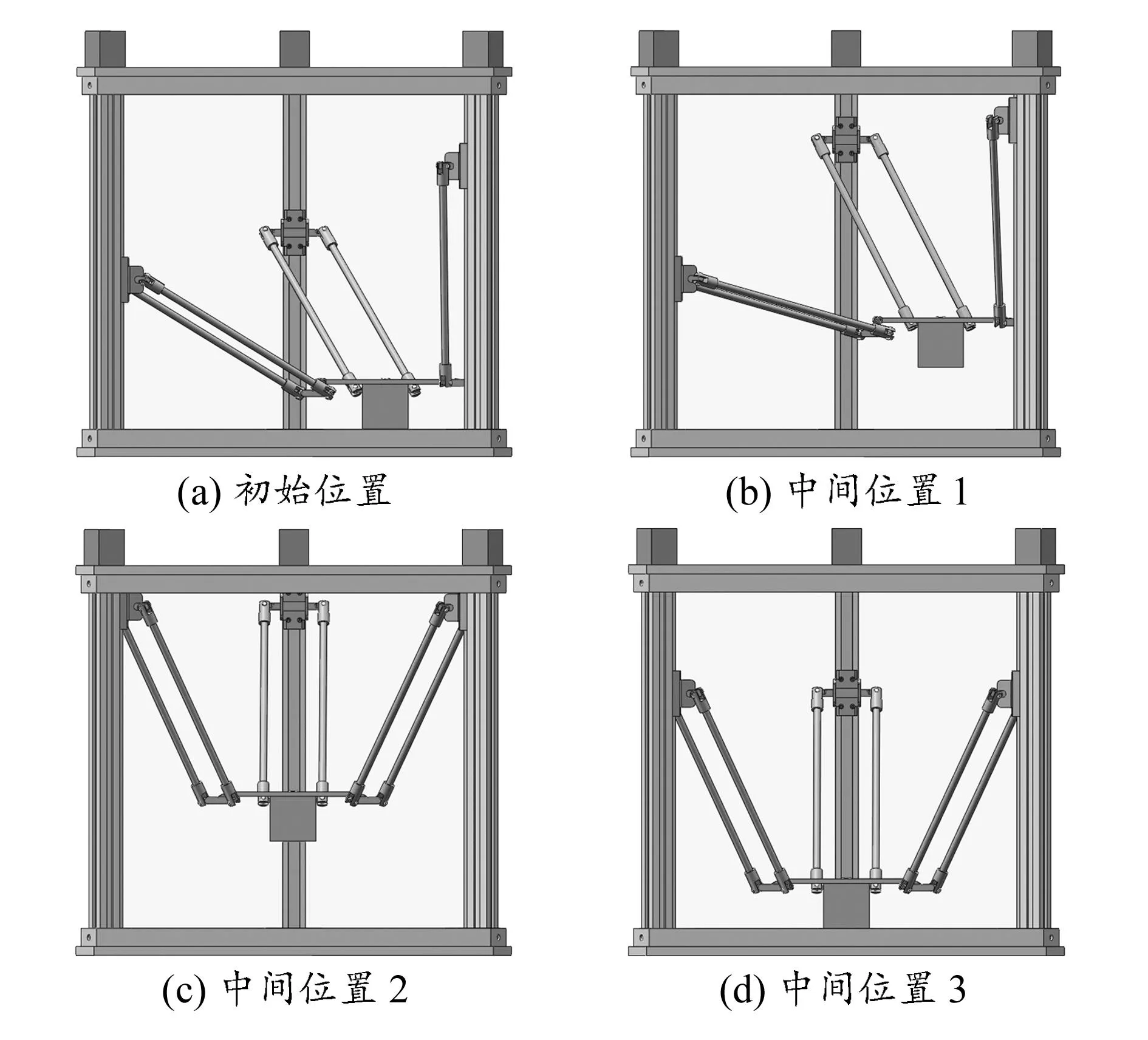
图10 动态仿真算例

7 结束语

本文构造了一种对称分布的新型3PRPaR并联机构,分析了机构的动平台执行末端运动特性,结果表明,机构能够沿着空间x、y、z方向运动,不存在转动的情况。

基于雅可比矩阵推导得到正解奇异性和逆解奇异性条件,要求支链1、 2、3的移动副的垂直高度和动平台避免在同一高度,且主动副避免运动到极限位置,另外结构参数要求r+L>R。

通过NSGA-Ⅱ多目标优化算法优化,结果表明:工作空间体积和全域性能指标是背离的,而全域性能指标较大时,全域性能波动指标也较大。