网格尺寸效应对蜂窝空腹楼盖静力性能的影响
彭斯宁,杨晓华,何嘉杰,张泽良,刘宇杰
(湖南工业大学 土木工程学院,湖南 株洲 412007)
0 引言
空间结构[1]是形态呈三维立体状态,在载荷作用下具有三维传力特性[2],即表现为三维空间工作[3]的形态。空腹夹层板[4]是马克俭教授团队自主提出并创新研制成功的一种新型空间结构,这种结构具E-mail:464644503@qq.com有良好的受力性能,并被广泛运用于实际工程[5]中,理论分析也得到了充分验证。正六边形蜂窝型空腹夹层板[6]是马克俭教授提出的新型结构类型,它是由肋梁围成正六边形的蜂窝状造型单元,该结构不仅安全度较高,变形较小,而且造型独特,结构美观。李莉等[7]通过对比各结构类型楼盖研究得出,不同结构类型楼盖板跨中挠度基本相同,但内力传递方式不同,正六边形蜂窝型空腹夹层板楼盖空腹率较高,蜂窝型空腹夹层板楼盖结构自重和钢筋用量都是最小的。才琪等[8]采用子空间迭代法计算六边形蜂窝型钢筋砼空腹夹层板楼盖的基频和各阶振型,发现高跨比、空腹率和密柱截面边长对空腹夹层板楼盖基频的影响程度都大于5%,属于主要因素。徐金涛等[9]对上、下肋对蜂窝形钢筋混凝土空腹夹层板挠度的影响进行了分析,研究结果表明上、下肋刚度越大,蜂窝形钢筋混凝土空腹夹层板的挠度就越小。晁亚茹等[10]通过对蜂窝型钢网格楼盖进行了参数化动力分析,分析了剪力键宽度、钢空腹桁架高度、表层楼盖板和上、下弦梁对结构自振特性的影响。
通过上述分析可知,现有的正六边形蜂窝型空腹夹层板楼盖结构研究较为完善[11],但是关于混凝土结构部分[12-13]和钢结构部分[14-15]对于空腹夹层板楼盖的整体刚度影响尚未进行深入研究;另外,网格尺寸对蜂窝型空腹夹层板楼盖受力性能影响方面的研究并不深入。因此,本文拟采用有限元分析方法,通过对比分析,研究不同网格尺寸对楼盖承载力的影响,并分析混凝土结构以及钢结构对于楼盖整体刚度的影响,以期为该结构的工程实际应用提供参考依据。
1 基本模型
1.1 工程概况
正六边形蜂窝型空腹楼盖通常使用的剪力键形式有Y 字形、三角形和圆环形等形状,其中三角形与圆环形剪力键构造如图1所示。
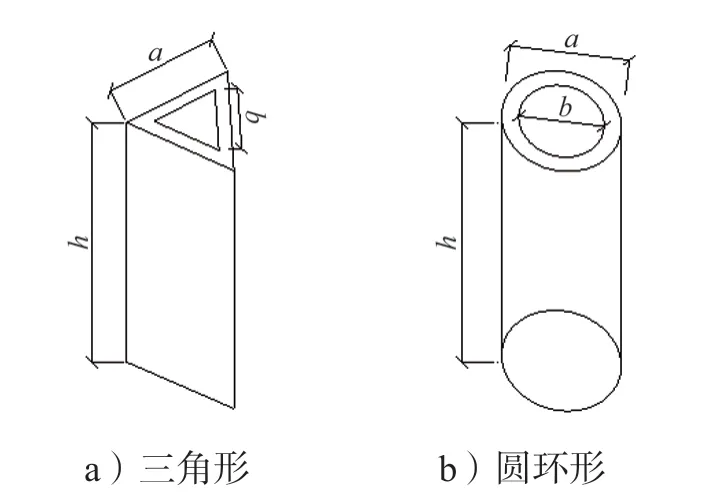
图1 三角形与圆环形剪力键构造图Fig.1 Diagram of triangular shear bond and torus shear bond construction
而Y 字形剪力键相较于其他形式的剪力键,其与空腹梁上、下翼缘接触面较大,三向抗弯刚度较大,更符合正六边形蜂窝楼盖三向传力的特点,能有效改善剪力键与肋梁连接处的应力分布,减少应力集中,提升空腹夹层板楼盖的整体刚度。
正六边形钢-混凝土空腹夹层板楼盖分为上下两部分,其中上部为混凝土板,下部由上、下肋钢结构梁组成,上、下肋均为T 型截面;剪力键为Y 字形截面钢,截面尺寸厚度与上、下肋T 型截面腹板厚度一致。上、下肋钢结构由剪力键连接,Y 字形剪力键构造如图2所示。
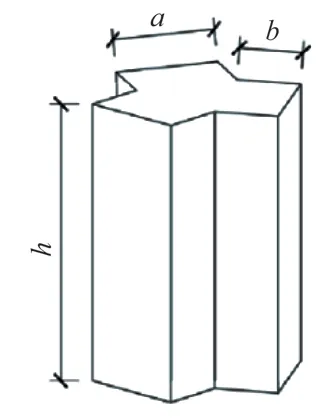
图2 Y 字形剪力键构造示意图Fig.2 Y-shaped shear key construction diagram
空腹夹层板楼盖结构剖面图如图3所示。
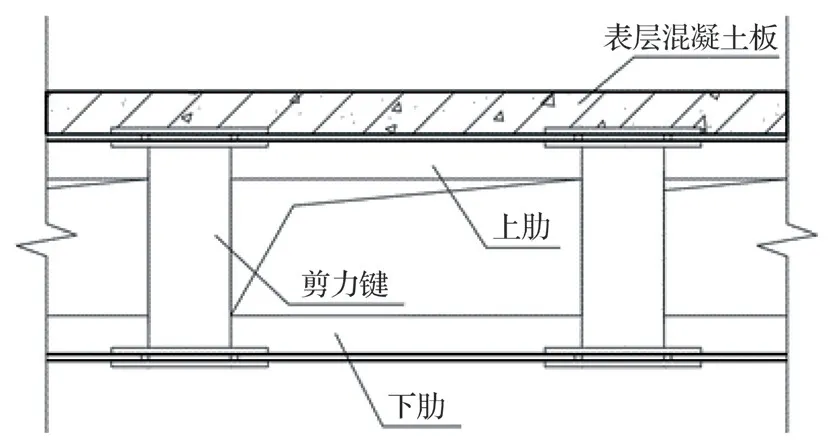
图3 空腹夹层板楼盖结构剖面图Fig.3 Structural profile of hollow sandwich floor
在有限元分析中,为了体现混凝土表层板以及钢结构对于楼盖整体刚度的贡献,对混凝土表层板采用SOLID65 单元,上、下肋梁及剪力键均采用SOLID185 单元,具体的构件参数及截面尺寸见表1。
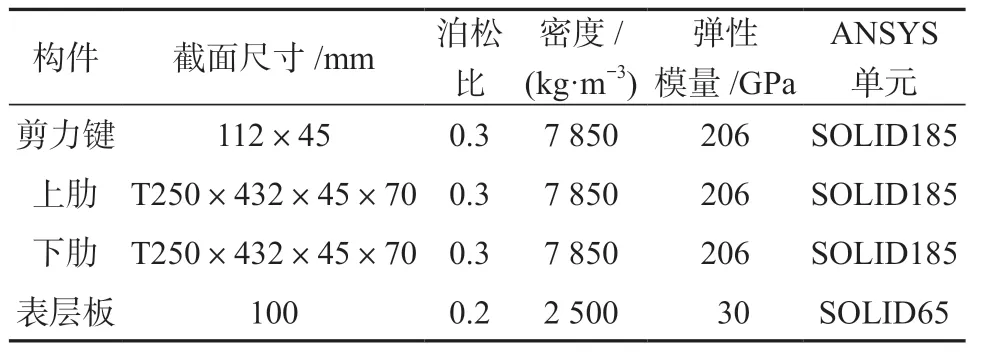
表1 各构件参数及单元选用Table 1 Parameters and unit selection of each component
为了有效研究正六边形蜂窝型空腹夹层板楼盖的网格尺寸效应,使其在受到竖向均布荷载作用时,分析不同网格尺寸对应挠度曲线状态以及受力性能,本研究中建立了跨度在30 m 左右的矩形楼盖,楼盖网格采用边长为1.0~4.5 m 的正六边形,使在仅受网格尺寸长度与跨度之比改变而其余条件均一致的情况下,建立了8 组正六边形蜂窝型空腹夹层板楼盖对照模型,以进行对照分析。其平面布置跨度尺寸见表2。为进一步深入研究网格尺寸大小对楼盖承载力的影响,每组楼盖网格分别建立一组网格尺寸相同的对照组-正交正放正方形钢-混凝土空腹楼盖的对比模型。
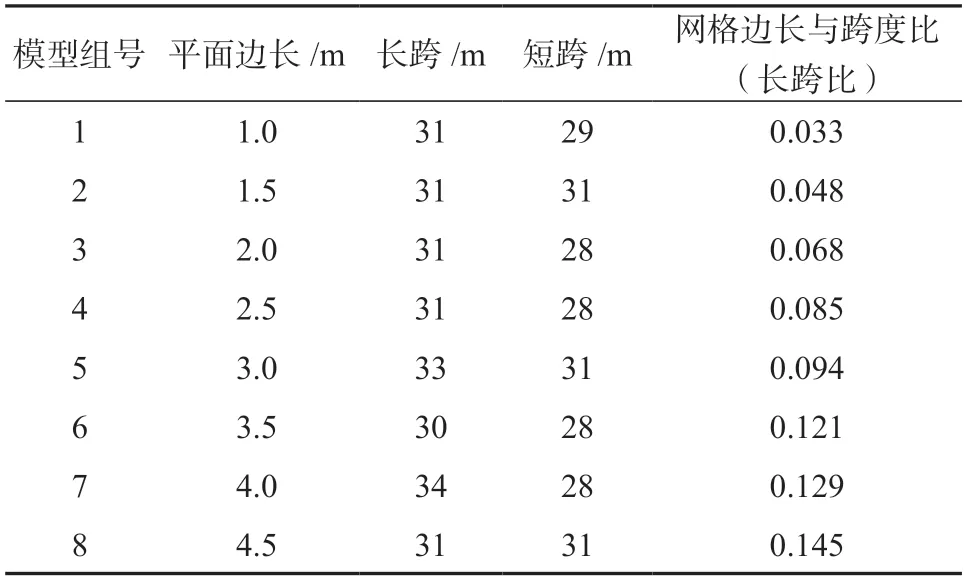
表2 平面布置跨度尺寸表Table 2 Plane layout span dimension table
以六边形网格边长为3.5 m,即长跨比为0.121的模型为例,构建如图4所示的平面布置图(图中尺寸单位为mm),其长跨为30.31 m,短跨为28.00 m,网格边长为3.5 m,材料参数以及截面尺寸详见表1,图4 为对照正交正放网格模型的平面布置图。对每组特定的模型,仅改变其长跨比,通过观察楼盖的整体位移,研究其静力变化以及网格尺寸效应。
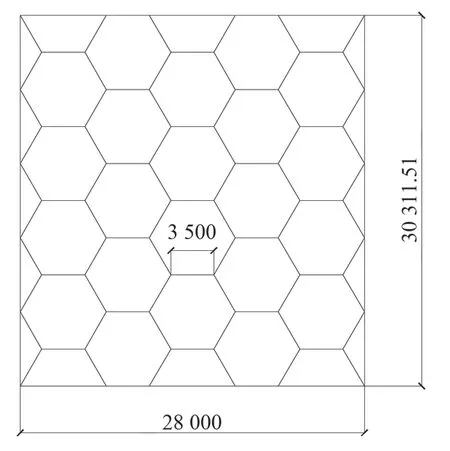
图4 第6 组模型平面布置图Fig.4 Layout plan for group 6 model
1.2 对照模型
空腹夹层板楼盖的结构形式与大部分楼盖的结构形式有明显区别,为了进一步研究尺寸效应如何影响正六边形蜂窝型空腹夹层板结构的整体刚度,以及正六边形蜂窝型网格形式的尺寸效应与其他不同网格形式尺寸效应的差别,对照正六边形蜂窝型网格,建立了一个正交正放网格结构模型进行对比分析。通过对不同网格形式的尺寸效应进行对比,以对空腹夹层板结构的网格尺寸效应有更深层次的理解。对每组特定的模型,仅改变长跨比,通过观察楼盖的整体位移,研究其静力变化以及网格尺寸效应。如图5为对应正六边形网格第6 组结构模型网格尺寸大小而建立的对照正交正放网格结构模型的平面布置图。

图5 第6 组对比模型平面布置图Fig.5 Comparison model layout plan for group 6
2 有限元分析
2.1 模型建立
根据分析要求建立有限元结构分析模型,结构模型的构件参数和单元的选用如表1所示。
对于有限元结构分析,钢结构上肋T形截面钢梁、下肋T 形截面钢梁和Y 字形剪力键采用SOLID185六面体实体单元进行网格划分,正六边形蜂窝型网格上、下肋钢梁划分为4 个单元,与上、下肋钢梁连接的剪力键高度为800 mm,划分为5 个单元。剪力键和上、下肋梁的连接网格划分如图6所示。整个空腹夹层板结构上、下肋梁均划分为348 个单元,剪力键划分为66 个单元,正六边形蜂窝型空腹夹层板的钢结构部分总共划分为678 个有限单元。有限元分析模型中钢结构部分网格划分情况如图6所示
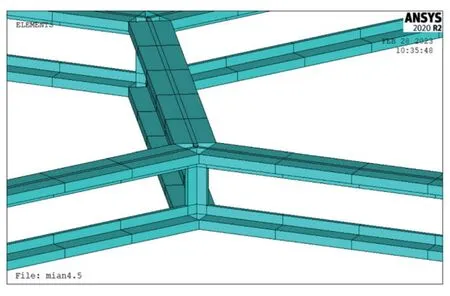
图6 钢结构空腹夹层梁的网格划分图Fig.6 Steel structure fasting sandwich beam meshing
混凝土表层板的网格划分采用SOLID65 实体单元,六边形网格区域以板中点为节点向六边形角点连线将其均匀划分成4 面体网格单元,对于楼盖边界以及混凝土表层板与下部分钢结构连接处的网格划分进行适当加密。建立的正六边形网格整体有限元结构模型网格划分如图7所示。

图7 正六边形网格整体有限元结构模型的网格划分Fig.7 Regular hexagon mesh finite element structure model meshing
作为对比,建立了同等网格尺寸大小的正交正放网格空腹夹层板有限元结构分析模型,该模型有限单元的选取和网格划分方法同正六边形空腹夹层板楼盖,建立的正交正放网格空腹夹层板楼盖有限元结构模型网格划分如图8所示。

图8 正交正放网格有限元结构模型的网格划分Fig.8 Orthogonal orthostatic mesh finite element structure model meshing
2.2 静力分析
在有限元分析结构中,考虑到实际工程中的工作情况,为正六边形蜂窝型空腹夹层板结构添加四边简支约束,即在有限元分析时对楼盖底部周边所有节点均施加X、Y、Z轴3 个方向位移为0 的边界条件。
结构分析过程中,对楼板面施加均布压力荷载,恒载按3.5 kN/m2输入,活荷载按2.0 kN/m2输入。并考虑结构自重,根据《建筑结构可靠性设计统一标准》GB 50068—2018,准永久组合:1.0DL+0.5LL;基本组合 1.3DL+1.5LL(DL 代表恒载,LL 代表活荷载)。分别计算结构的应力和变形,提取相应结果。通过有限元分析得到正六边形蜂窝型空腹夹层板结构在四周简支情况下的竖向位移云图(如图9所示)和应力应变。
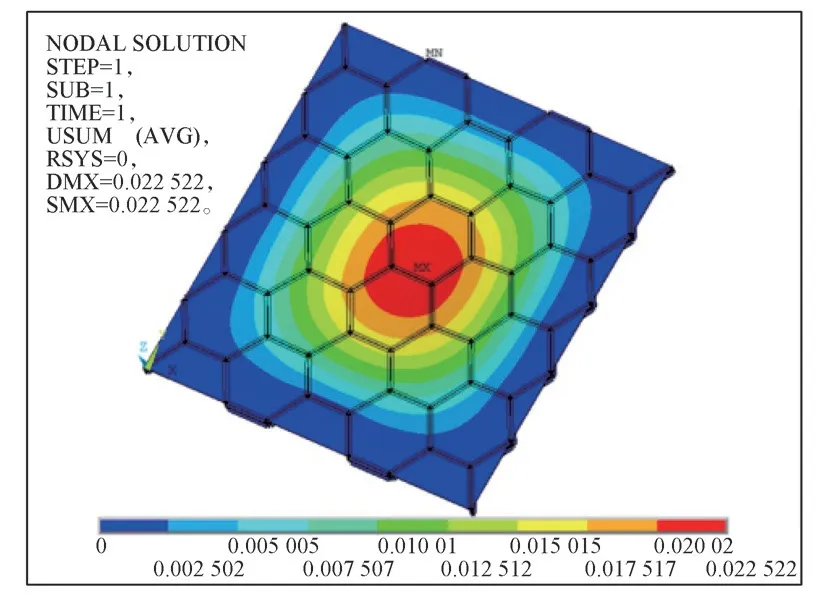
图9 四边简支正六边形蜂窝空腹夹层板楼盖竖向位移云图Fig.9 Vertical displacement cloud map of four-sided simply supported regular hexagonal honeycomb hollow sandwich slab floor
由图9所示结构有限元分析结果可知,正六边形蜂窝型空腹夹层板的竖向位移分布与实心板在同样条件下的竖向位移分布类似,说明计算结果基本合理,实际模型的中心最大位移为22.52 mm,支座最小位移为0 mm,最大挠度与跨度的比值为1/1 332,满足《混凝土结构设计规范》 GB 50010—2010 规定1/300 的限值,说明正六边形蜂窝型空腹夹层板整体抗弯刚度大,具有很好的承载能力。
2.3 正六边形模型网格尺寸对整体位移的影响
每一组对比模型中,依据选取不同网格尺寸建立有限元分析结构模型,计算不同网格尺寸正六边形蜂窝型空腹夹层板楼盖在竖向荷载作用下的竖向位移,从而找出网格尺寸对于正六边形蜂窝型空腹夹层板楼盖整体刚度的影响,不同网格尺寸模型的最大挠度如表3所示。
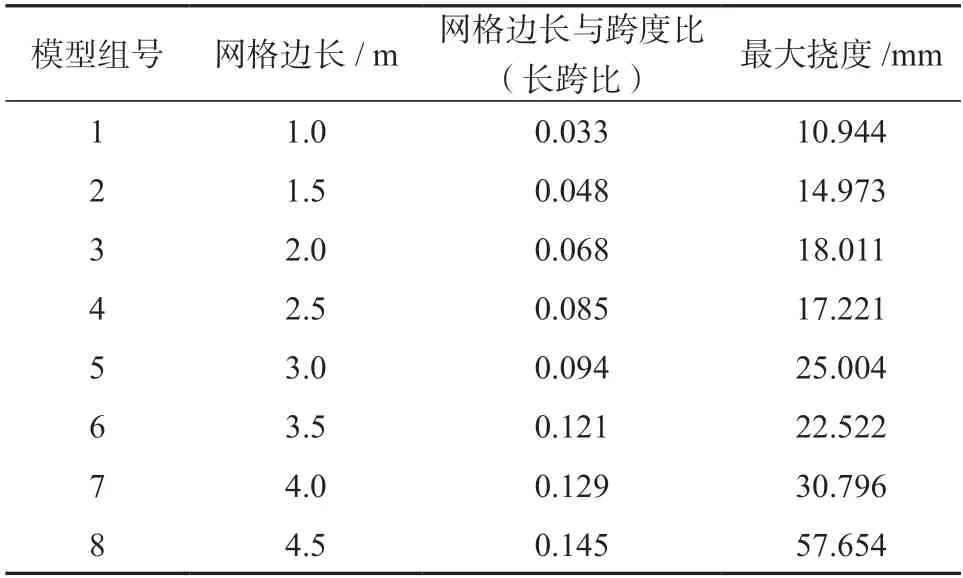
表3 正六边形蜂窝型空腹夹层板最大挠度与网格尺寸对应值Table 3 Maximum deflection and corresponding grid size of the hexagonal honeycomb fasting sandwich plate
由表3 可得,正六边形网格蜂窝楼盖在当网格边长为1 m 时,即网格边长与跨度比为0.033 时,结构的跨中最大挠度为10.944 mm,挠度与跨度的比值为1/2 741;当网格边长为4.5 m 时,即网格边长与跨度比为0.145 时,结构的跨中最大挠度为57.654 mm,挠度与跨度的比值为1/538。二者之间跨中最大挠度的比值接近5.4 倍,可以看出,随着网格尺寸与跨度之比的增加,正六边形网格空腹夹层板楼盖整体刚度随之减少,在不改变竖向荷载的情况下,楼盖跨中最大挠度会逐渐增加。
2.4 正交正放模型网格尺寸对整体位移的影响
每一组正交正放网格对比模型的网格尺寸和跨度与对应正六边形蜂窝型网格尺寸相同,依据选取不同网格尺寸建立有限元分析结构模型,计算不同网格尺寸正交正放网格空腹夹层板楼盖在竖向荷载作用下的竖向位移,从而找出网格尺寸对于正交正放网格空腹夹层板楼盖整体刚度的影响,不同组模型的最大挠度如表4所示。
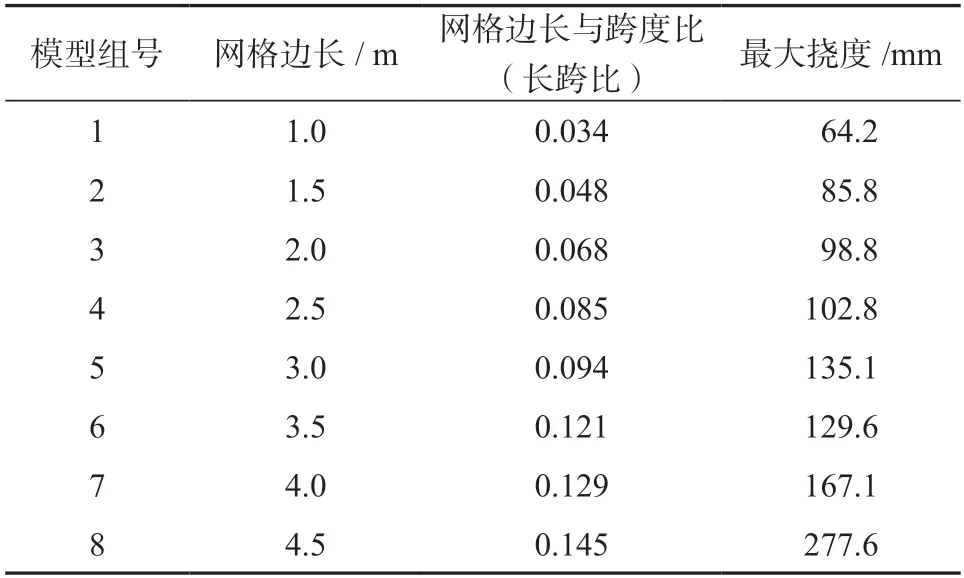
表4 正交正放网格空腹夹层板最大挠度与网格尺寸对应值Table 4 Maximum deflection and corresponding value of grid size of the orthogonal grid fasting sandwich plate
2.5 正六边形网格与正交正放网格尺寸效应对比分析
为了对比分析正六边形网格蜂窝型空腹夹层板楼盖和正交正放网格空腹夹层板楼盖的网格尺寸效应,以及研究在不同网格形式下网格尺寸效应对于空腹夹层板楼盖整体抗弯刚度的影响,对正六边形网格蜂窝型空腹夹层板和正交正放网格空腹夹层板跨中最大挠度与长跨比变化关系进行拟合对比分析,得到的最大挠度-长跨比变化关系曲线如图10所示。
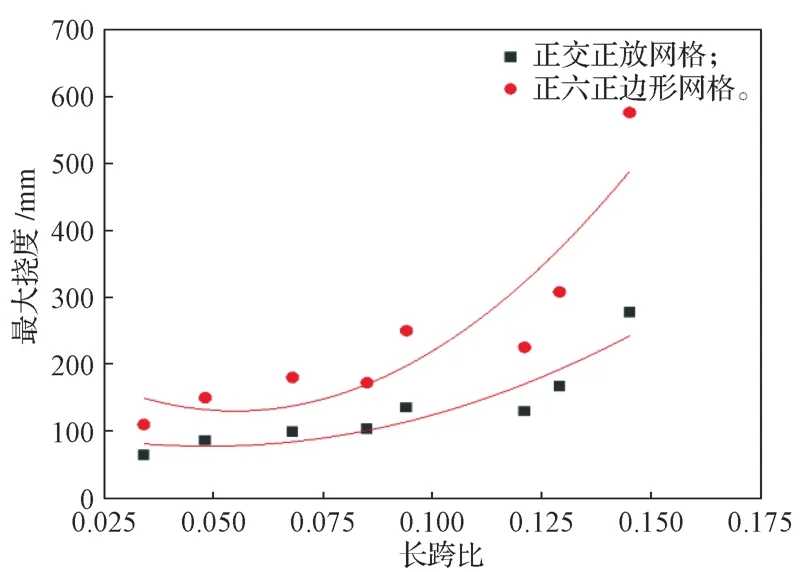
图10 不同网格形式下长跨比与最大挠度关系曲线Fig.10 Curves of the relationship between the maximum deflection of different mesh forms and the length span ratio
正六边形网格蜂窝楼盖每组模型在仅改变长跨比的情况下,施加相同的荷载,得到对应的最大位移,并以最大挠度为纵坐标、长跨比为横坐标,进行数据分析。随着长跨比增加,在自重以及固定面荷载的作用下,楼盖的最大挠度不断增加,由此可以说明,网格尺寸大小可以影响楼盖的整体抗弯刚度;长跨比越大,楼盖刚度越小。由表3、表4 和图10 可得,正六边形网格蜂窝楼盖在其他条件不变的情况下,当长跨比为0.033~0.068 时,楼盖跨中挠度缓慢增加;当长跨比继续提升至0.068~0.125 时,跨中最大挠度略有提高但整体保持水平变化趋势;但当长跨比超过0.125 后,楼盖跨中最大挠度迅速增加。
当长跨比较小时,即网格尺寸较密时,楼盖的整体刚度主要来源于下部的钢结构,混凝土表层板对于整体的受力影响较小,但由于单位面积内钢结构的密度较大,因此楼盖整体的刚度表现出色;而当长跨比进一步增加,钢-混凝土共同作用的能力得到充分发挥,此时空腹夹层板的整体刚度主要来源于钢-混凝土共同作用,此时能充分发挥正六边形蜂窝型空腹夹层板楼盖的结构优点;但随着长跨比超过一定范围后,单位面积内网格密度下降,钢-混凝土共同作用效果下降,此时楼盖的整体刚度主要由混凝土表层板提供,楼盖整体刚度迅速下降,跨中最大挠度迅速提升。
正交正放网格空腹夹层板网格边长与楼盖跨中挠度在一定程度上同样成正相关,但其变化关系曲线要明显比正六边形空腹夹层板的变化关系曲线平缓;说明正交正放网格空腹夹层板的网格尺寸效应要明显小于正六边形网格空腹夹层板,而其钢-混凝土共同作用的表现并没有正六边形蜂窝型空腹夹层板的表现充分,正六边形蜂窝型空腹夹层板楼盖的网格优势和三向受力的结构优点在网格尺寸效应上明显优于正交正放网格空腹夹层板楼盖。
通过拟合曲线对比图10 可以看出,两种网格布置的空腹夹层板楼盖最大挠度随着长跨比之间的变化趋势大致相同,但正交正放网格的变化幅度较正六边形网格的小。由此可以看出,对于网格尺寸相同的正交正放网格空腹夹层板,其尺寸效应要小于正六边形蜂窝型空腹夹层板,这是由于正交正放网格的空腹夹层板楼盖用钢量较正六边形网格空腹夹层板楼盖大,突出了正交正放网格空腹夹层板楼盖的钢结构在整体结构中的作用。
2.6 混凝土表层板厚度对网格尺寸效应的影响
混凝土表层板厚度对于空腹夹层板整体竖向刚度有较大的影响,随着混凝土表层板厚度增加,空腹夹层板的整体竖向刚度随之增加。为进一步研究不同网格尺寸下混凝土表层板厚度对正六边形蜂窝型空腹夹层板楼盖抗弯刚度的影响,基于建立的正六边形蜂窝型空腹夹层板楼盖的有限元分析模型,控制构件其它参数保持恒定,而仅改变混凝土表层板的厚度,研究混凝土表层板厚度对于正六边形空腹夹层板不同网格尺寸的影响。
分别取80,90,100,110,120 mm 建立5 组有限元分析模型组,每组模型中包含8 个不同网格尺寸的有限元分析结构模型,共建立了40 组有限元结构分析模型。分析得到的不同楼板厚度下楼盖跨中最大挠度如表5所示。以网格边长与跨度比为横坐标,空腹夹层板的跨中最大位移量作为纵坐标,将混凝土表层板厚度从80 mm 到120 mm 所得到的空腹夹层板的跨中最大竖向位移量相连接,得到如图11所示不同混凝土表层板厚度的正六边形空腹夹层板楼盖跨中最大挠度随网格边长与跨度比(长跨比)变化曲线。
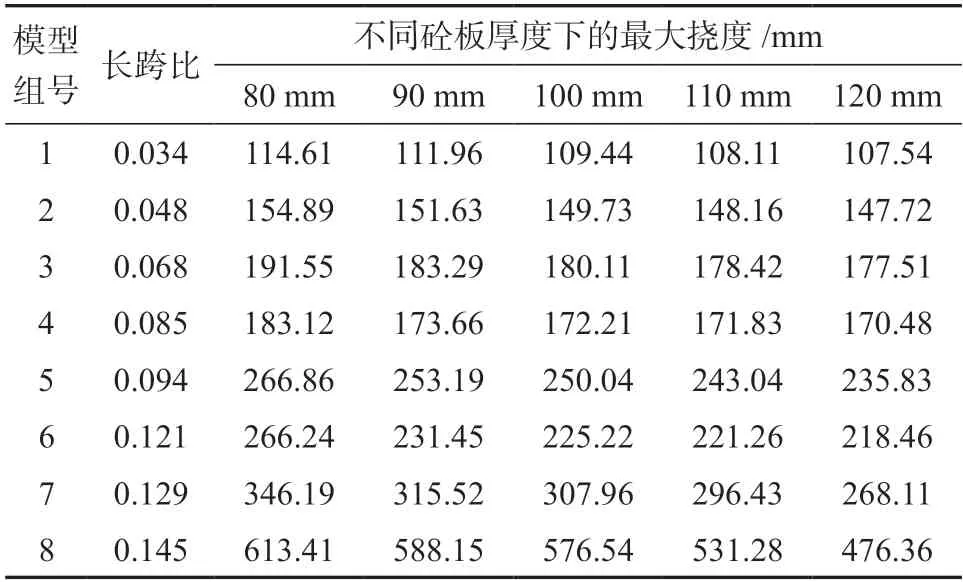
表5 不同混凝土表层板厚度下长跨比与最大挠度对应值Table 5 Corresponding values to the length span ratio and maximum deflection under different concrete surface slab thicknesses
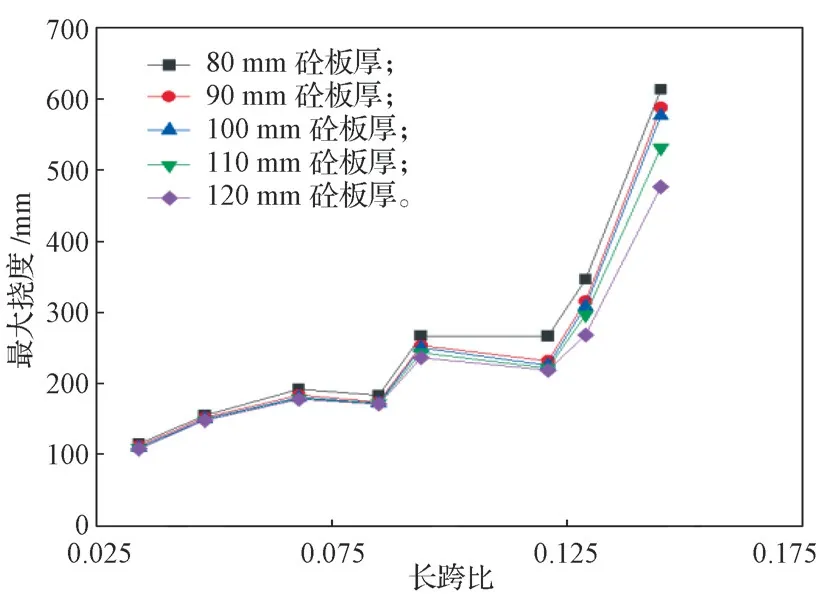
图11 不同混凝土表层板厚度下长跨比与最大挠度关系曲线Fig.11 Relationship curves of the length span ratio and maximum deflection under different concrete surface slab thicknesses
结合表5 和图11 可以得出,随着混凝土表层板厚度的增加,正六边形蜂窝型空腹夹层板楼盖跨中最大挠度值不断降低。当长跨比为0.033~0.068 时,正六边形蜂窝型空腹夹层板楼盖跨中最大挠度随混凝土表层板厚度增加而降低,而其最大挠度随网格尺寸增加的变化趋势基本保持一致,此时楼盖的整体刚度主要来源于下部的钢结构,混凝土表层板对于楼盖整体受力影响较小,此时,不同混凝土表层板板厚的跨中最大挠度也十分接近。
当长跨比处于0.068~0.125,混凝表层板板厚为80 mm 时,跨中最大挠度随着网格尺寸的增加速度要明显大于其他不同混凝土表层板板厚,随着混凝土表层板板厚的下降,混凝土表层板对于正六边形蜂窝型空腹夹层板楼盖整体受力影响也会降低,此时,随着网格边长与跨度之比的增加,钢-混凝土的共同作用会提前下降。
3 结论
本文对钢-混凝土正六边形蜂窝型空腹夹层楼盖正六边形不同网格尺寸下的抗弯刚度和网格尺寸效应进行了研究。不同尺寸的正六边形蜂窝结构会影响其力学性能,并将正六边形网格空腹夹层板楼盖的尺寸效应与正交正放网格空腹夹层板楼盖的尺寸效应进行对比分析,得出如下结论:
1)正六边形蜂窝型钢-混凝土空腹夹层楼盖结构的荷载传递、分配合理可靠,荷载三向传递,结构构件之间具有良好的协同性,楼盖整体刚度较大。
2)正六边形蜂窝型空腹夹层板网格边长与楼盖跨中挠度在一定程度上成正相关。在其他条件不变的情况下,当长跨比为0.033~0.068 时,楼盖跨中挠度缓慢增加;当长跨比为0.068~0.125 时,跨中最大挠度略有提高,但变化趋势基本接近水平;但当长跨比超过0.125 后,最大挠度迅速增加。在正六边形蜂窝型空腹夹层板长跨比较小时,即网格尺寸较密时,楼盖的整体刚度主要来源于下部的钢结构,混凝土表层板对于整体的受力影响较小;而当长跨比进一步增加,钢-混凝土的共同作用慢慢提高。
3)当混凝土表层板厚度在一定范围内,随着混凝土表层板厚度的增加,其网格尺寸效应减小,而当混凝土表层板厚度小于一定值时,其钢-混凝土的共同组合作用会被削弱。

