不定方程13x2-11y2=2和48y2-13z2=35的公解

朱文娜,牟全武

(西安工程大学理学院, 陕西 西安 710048)

0 引言

不定方程是数论研究的重要对象,为了研究实二次域的Gauss类数问题,人们需要求解一类特殊的二次不定方程—Pell方程。自20世纪40年代至今,关于两个Pell方程的公解问题已有大量研究(如文献[1-7]),这使得一些特殊的二元四次不定方程得到完全解决。从研究方法上看,除了综合运用递推序列及二次剩余等初等方法[8-9],还可以借助Gel’fond-Baker方法及Diophantus逼近等高等方法[10-11]。

设a1,a2,a3为正整数,且满足任意两数之积与1的和为完全平方数。关于不定方程组

(1)

的求解引起不少人的兴趣。1969年,Baker和Davenport[2]证明了当(a1,a2,a3)=(1,3,8)时,不定方程组(1)仅有正整数解(x,y,z)=(1,1,1),(11,19,31);1997年,陈志云[12]给出了当(a1,a2,a3)=(7,9,32)时不定方程组(1)的正整数解的上界;2008年,郑兆顺[13]给出了当(a1,a2,a3)=(9,11,40)时不定方程组(1)的正整数解的上界;2022年,李杨[14]给出了当(a1,a2,a3)=(8,10,36)时不定方程组(1)的正整数解的上界。2011年,贺腊荣[15]证明了当(a1,a2,a3)=(11,13,48)时不定方程组(1)的正整数解满足x<0.92×2418393,y<2418393,z<1.92×2418393。本研究的目的是改进文献[15]中的结果,利用Gel’fond-Baker方法及Diophantus逼近方法,我们证明了

定理1不定方程组

(2)

的全部解为(x,y,z)=(±1,±1,±1),(±551,±599,±1 151)。

1 预备工作

x2-Dy2=M

(3)

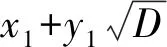
x2-Dy2=1

(4)

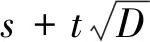
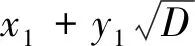
x1x2-Dy1y2≡0(mod|M|),x1y2-x2y1≡0(mod|M|)．

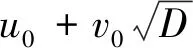
且方程(3)的属于结合类K的全部解可由

表出。

方程组(2)可化为

将13x与13z分别视作x,z,则只需求解方程组

(5)

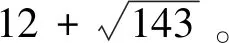
(6)

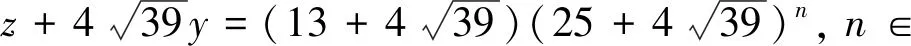
(7)

或

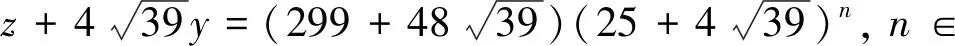
(8)

由以上分析,只需要分别考虑式(6)和式(7)同时成立或者式(6)和式(8)同时成立这两种情形。当m=0时,由式(6)得(x,y)=(13,1),代入方程组(5),得到(5)的一组正整数解(x,y,z)=(13,1,13);当m=1时,由式(6)得(x,y)=(299,25),代入方程组(5),无解;当m=2时,由式(6)得(x,y)=(7 163,599),代入方程组(5),得到式(5)的一组正整数解(x,y,z)=(7 163,599,14 963)。故当0≤m≤2时得到方程组(2)的两组正整数解(x,y,z)=(1,1,1),(551,599,1 151)。下文中将证明m≥3时,式(6)和式(7)不能同时成立,式(6)和式(8)亦不能同时成立,故此种情形下方程组(2)无解。我们采用反证法,仅对式(6)和式(7)同时成立的情形进行详细讨论,对式(6)和式(8)同时成立情形的讨论是完全类似的,故略去。

2 Gel’fond-Baker方法的应用

注意m≥3,n∈。为叙述方便,令

经计算知P>28 700,Q>1。根据式(6)及式(7)得

故P>Q且

(9)

由式(9)推出

即

(10)

用下述引理3证明若式(10)成立,则必有m<1027。

这里d=[(α1,α2,…αk):

引理3的证明见文献[17]第20页。

令

(11)

(12)

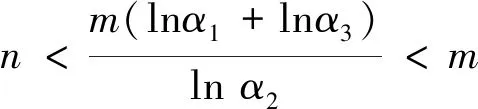
(13)

(14)

显然d=[(α1,α2,α3):]=[]=4。

容易验证代数数α1,α2,α3所满足的极小多项式分别是

这给出A1=24,A2=50,A3=813 120。又由式(13)得B=max{m,n,1}=m。根据引理3推出

-ln|Λ|<19210ln(24)ln(50)ln(813120)ln(m)

(15)

由式(14)及式(15)知

但当m≥1027时此不等式不成立,故必有m<1027。

3 Diophantus逼近方法的应用

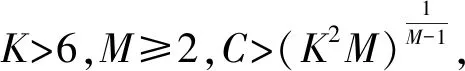
(16)

则不存在整数m,n同时满足

(17)

|mθ-n+β|

(18)

引理4的证明见文献[2]第133～134页。

令

这里α1,α2,α3由式(11)给出。由式(12)得 |mθ-n+β|<0.1C-m

(19)

设

θ0=0.812 019 300 234 695 763 189 497 317 209 119 603 268 924 900 197 531 476 104 505,

取p/q为θ0的渐近分数,q≤1031且q最接近1031。根据Dirichlet逼近定理得|qθ0-p|≤10-31。经计算知

注意

根据引理4,当26≤m<1027时式(19)不成立。故只需考虑3≤m≤25的情形。

θ有连分数的渐近分数序列

取q=117,p=95,φ=qθ-p。经计算知

|φ|=0.006 258 13…,‖qβ‖=0.475…

(20)

由式(19)得

|m(p+φ)-qn+qβ|<0.1qC-3<0.002.

故当3≤m≤25时,有

‖qβ‖=‖m(p+φ)-qn+qβ-mφ‖

≤‖m(p+φ)-qn+qβ‖+m‖φ‖

=|m(p+φ)-qn+qβ|+m|φ|

<0.002+25×0.007

=0.177,

这与式(20)矛盾。

综上讨论,m≥3时式(6)和式(7)不能同时成立,同理可证式(6)和式(8)也不能同时成立,故定理1得证。