已知波形信号的时差频差估计方法研究与性能分析

刘 严 朱 毅 张 源 郭福成

（国防科技大学电子科学学院，湖南长沙 410073）

1 引言

无源定位问题广泛存在于电子侦察、海上救援等领域，具有应用范围广、技术性强等特点。常用的无源定位方法包括测向交叉定位、多站时差定位等［1-4］。当观测站与辐射源之间存在相对运动时，不同观测站接收信号的载频会有所差异，为无源定位提供了可用的频率多普勒信息。基于多站信号时差、频差的无源定位方法具有较高的定位精度，得到了很多的关注和研究［5-10］。已有成果主要集中在基于时频差的无源定位方法研究、性能分析和快速算法研究等方面。

无论用于辐射源定位的侦察站数量是两个还是多个，对两两侦察站之间的时差和频差进行高精度估计都是时频差定位方法的基本步骤。目前最常用的双站时差频差估计方法是基于观测信号互模糊函数（Cross-Ambiguity Function，CAF）的方法［11-14］。该方法是极大似然方法的一种近似实现方式，在未知信号波形的情况下，可以得到逼近克拉美-罗界（Cramer-Rao Lower Bound，CRLB）的参数估计精度［12-13］。但是，对于不同的信号模型，时差频差估计精度的CRLB是有显著区别的。文献［15］对比了平稳随机信号、未知确定信号和已知信号等不同条件下的时差频差估计CRLB，结果表明信号波形先验信息有助于大幅提高时差频差估计精度。

在很多实际应用中，待定位电子目标所辐射的信号波形是先验已知的，例如对数字广播信号等民用目标的定位问题［16-19］。当已知波形的参考信号同时被多个运动接收站所截获时，会在观测信号中引入未知的幅度增益和时差、频差等因素，导致每个观测站侦收的信号都与原始参考信号之间存在差异。如何利用好参考信号波形的先验信息，并尽可能消除各种不确定性因素的影响，是针对已知波形信号实现时差频差估计和无源定位需要着重解决的问题。文献［8］基于信号波形先验已知的假设，推导了这种情况下时差频差估计的CRLB。但由于该成果侧重于比较电磁信号与水声信号时差频差估计问题的异同，对信号接收模型的描述有所简化，与实际应用场景存在一定偏差。

本文研究已知参考信号波形条件下的双站时差频差被动估计问题，提出相应的参数估计方法，并对参数估计精度的CRLB进行分析。该双站时频差估计方法可推广应用于多站系统，随后通过联合多组时差频差估计值实现对辐射源位置的估计。在侦察信号建模过程中，借鉴文献［15］中的模型对运动接收站的时延和频移效应进行描述，从而将时差、频差参数与参考信号波形分离开来，使得接收站观测信号与已知的参考信号波形信息之间的关系更加直观可用。另外，通过把未知时差、频差参数与信号波形解耦合，在所得到的CRLB表达式中，各种模型因素的影响也能够更具体地分析。

全文共分为六部分。第二部分对双站接收信号进行建模，第三部分提出已知波形信号时差频差估计方法，第四部分深入分析信号波形已知条件下时差、频差参数估计的CRLB，第五部分仿真验证新方法的性能，并与推导得到的CRLB进行对比，第六部分总结全文。

2 双站信号接收模型

假设一个电磁信号被两个侦察站同时截获，在观测时间内辐射源与观测站之间的相对位移可以忽略，同时假设观测过程中信道传播损耗、天线增益等参数保持恒定，则可以认为两个接收站的观测数据是在一个确定的几何构型条件下采集得到的。

两个接收站的观测数据分别为

其中s1和s2表示观测信号波形，u1和u2表示信号采集过程中混入的随机高斯噪声。记N表示信号的采样点数，则式（1）和式（2）中各向量均存在于复数空间CN×1中。

假设侦察信号的原始波形先验已知，记为s0，两个接收站与辐射源之间相对运动造成的时差和频差分别为td1和fd1、td2和fd2，两个侦察站接收信号之间的时差和频差分别为td=td2-td1和fd=fd2-fd1。在模型描述和算法提出过程中，为简化叙述，用时差和频差的变形形式τ=td/T和v=2πfdT分别代替原始时差、频差两个物理量，其中T表示信号采样间隔。为表述方便，直接将这两个参数描述为“时差”和“频差”。相应地，其他单站时差、频差变量也替换为对应的变形形式，即τ1=td1/T，v1=2πfd1T，τ2=td2/T，v2=2πfd2T。

假设入射信号带宽远小于载频，则可以采用群延迟形式近似表示两个接收站所采集的观测数据，即将原始信号波形从时域变换到频域之后进行相移，以描述信号时延的效果［15］，得到两个接收站上观测信号的具体形式为

其中a1和a2表示两个接收站的信号增益，ϕ1和ϕ2分别表示两个接收站在采集信号时的初始相位，Dv1=diag{exp(jv1l)}，l=[0，1，…，N-1]Τ，diag{·}表示将向量元素作为对角线元素所得到的矩阵，Dv2=diag{exp(jv2l)}，，上标(·)Τ和(·)H分别表示转置和共轭转置运算。当信号相对带宽较大时，信号带宽内不同频率分量之间由频移造成的相移会有所不同，导致式（3）和式（4）中的信号表示形式存在一定的偏差。但是，对于实际应用中的各种常见信号，其相对带宽大多数都比较小，该偏差也可以忽略，因此本文沿用了这种近似的表示方法。

3 时差频差估计方法

由式（1）和式（2）不难看出，在假设信号片段s0先验已知的情况下，观测数据服从高斯分布，分布函数中的未知变量集合为

其中，a0=[a1，a2]Τ，θ1=[ϕ1，τ1，v1]Τ，θ2=[ϕ2，τ2，v2]Τ。待估计参数的信息包含在向量θ2-θ1中。观测数据x的分布函数为：

其中，CN(α，β)表示均值为α、方差为β的复高斯分布，，Q1=Dv1FHDτ1F，Q2=Dv2FHDτ2F，σ2表示两个接收站上观测数据的噪声功率。本文假设两个接收站上的噪声功率相等，如果两者不相等，也可以遵循本文思路得到相应的时频差估计方法和性能分析结果。

由于两个接收站的观测噪声u1与u2相互独立，幅度a1与a2依赖于电磁信号到达两个接收站的距离和传播损耗等互不相关的因素，因此也相互独立。类似地，变量集θ1与θ2也相互独立。因此可将式（6）中的分布函数改写为：

即优化τ和v以最大化概率函数p(x1，x2|ξ0；s0)的问题可以分解为对τ1与v1、τ2与v2分别进行优化的两个子问题，实现过程为

由式（8）和式（9）分别估计两站时延、频移的过程相同，以式（8）为例，该似然函数的具体形式为

将式（3）中s1的表达式代入上式，得到τ1与v1的估计式为

上述单通道时延、频移估计过程采用了与互模糊函数类似的实现方式。同样地，第二个观测站的时延、频移的估计式为

在具体实现过程中，通过遍历{τ，v}的可能取值范围，得到式（12）和式（13）中互相关函数最大幅值对应的坐标即为，依据式（10）可以进一步估计得到双站时差频差估计值，经线性变换可最终获得时差频差估计值

上述方法通过估计两站观测信号相对于已知参考信号的时延、频移，并计算两者差分来估计双站时差、频差，其计算量主要集中在基于互模糊函数的两站时延、频移估计部分。仅考虑两次时延、频移估计过程的计算复杂度，以复数乘法次数统计新方法的计算量，并记时频差搜索估计过程中时差-频差二维网格点数目为K，得到新方法的计算复杂度对比情况如表1所示。

表1 新方法的计算复杂度Tab.1 Computational complexity of the new method

4 时差频差估计精度的CRLB分析

对参数估计精度的CRLB进行分析可以方便评估不同方法的优越性，并反映各种因素对参数估计性能的影响情况。然而，式（1）～式（4）给出的观测数据模型并没有建立观测数据与待估计时差频差参数之间的直接联系，给CRLB 分析造成了困难。本部分先对该信号模型进行改写，以建立直接依赖于双站时差频差的观测数据模型，随后基于该模型推导已知波形信号条件下的双站时差频差估计精度的CRLB，最后分析双站时差频差估计精度与对应的单站估计性能之间的关系。

4.1 依赖于双站时差频差的观测信号模型

为了方便对双站时差频差估计性能进行分析，有必要将双站时差和频差参数在观测信号模型中更直观地展现出来。为此，参考式（3）和式（4）的形式，建立双站接收信号之间的关联如下：

其中a=a2/a1表示两个接收站的相对信号增益，ϕ=ϕ2-ϕ1表示两个接收站在采集信号时的相对初始相位，

基于上述模型，将第二个接收站的观测数据由式（2）改写为

其中Q=DvFHDτF。在假设入射信号的相对带宽较小的情况下，双站时差频差之间满足QQ1≈Q2，因此式（15）与式（2）、式（4）给出的信号模型近似等价。

通过改写第二个接收站的信号形式，观测模型中的未知变量集合也随之发生了变化，新的变量集合为

其中，a=[a1，a]Τ，θ1=[ϕ1，τ1，v1]Τ，θ=[ϕ，τ，v]Τ。通过建立和利用第二个接收站信号与第一个接收站信号之间的联系，待估计参数τ和v更加直观地呈现在了观测数据模型中。

相应地，观测数据x的分布函数形式变化为：

4.2 时差频差估计精度的CRLB推导

依据式（6）得到观测数据x关于参数集ξ的Fisher信息矩阵Jξ为：

偏导数∂μ/∂ξ中的各个分块元素分别为：

其中，L=diag(l)，P1=Dv1FHLDτ1F，P=DvFHLDτF，0表示全0向量或矩阵，其维数可由上下文确定。

对上述表达式进行拼接，并通过数学计算得到

由式（22）可以看出，信号幅度参数a=[a1，a]Τ的估计精度与时差、频差和相位参数的估计精度之间相互独立。在式（18）和式（22）中，将信号幅度参数a当作冗余参数加以剔除，得到参数集对应的Fisher信息矩阵为：

进一步地，由矩阵求逆引理［20］，得到参数集θ的Fisher信息矩阵为：

对式（28）求逆，就可以得到参数集θ估计精度的CRLB 矩阵，其对角线元素分别表示ϕ、τ和v的估计值的均方误差下限，再经过线性变换，就可以得到两通道时差td和频差fd的CRLB。

综合式（24）～（28），将CRLB 表达式中与a1和a有关的变量抽出，可以得到CRLBθ与成反比，以及随a2单调减小的结论，表明两个通道接收信号的幅度越大，则时差、频差估计精度越高，这与参数估计性能的常识是吻合的。

4.3 与单通道参数估计性能的对比分析

在本文给出的双站时差频差估计方法中，首先利用参考信号波形先验信息估计两个观测站各自的信号时延和频移，然后依据式（10）对两通道参数估计值相减以得到双站时差和频差估计结果。相比而言，主动雷达的回波时延和频移估计可类比为已知波形条件下的单通道参数估计问题，也可看作是本文研究问题在a1=1 和θ1=[ϕ1，τ1，v1]Τ=0 条件下的简化情况。直观来看，双站时差、频差均未知时的信号模型中未知参数更多，比单通道时延、频移参数具有更强的不确定性，因此双站时频差估计精度比同等条件下雷达回波时延、频移估计精度会有所降低。以下借助定量分析证明这一结论。

由于观测数据x1和x2中的随机噪声相互独立，所以由式（8）和式（9）得到的两通道时延、频移估计值的估计误差之间也相互独立，因此

两通道时差和各自时延估计精度的CRLB对应于其估计方差的最小值，因此

类似地，两通道频差和各自频移估计精度的CRLB满足：

由于参数估计精度的CRLB均为正值，因此

经线性变换td=Tτ和fd=v/2πT之后，对时延、频移参数可得到相同结论。

上述结论也可以由上一小节给出的CRLB的定量分析结果得到。在假设a1=1 和θ1=[ϕ1，τ1，v1]Τ=0的条件下，通过与上一小节分析类似的过程，可以得到参数集θ=[ϕ，τ，v]Τ的Fisher信息矩阵为：

其中，s=a1ejϕ1Q1s0对应于该简化模型中的已知信号，简化后的Fisher信息矩阵表达式为

与已有成果一致。对该矩阵求逆，可以得到对应的参数估计精度CRLB为：

所得矩阵中各对角线元素即为参数集θ=[ϕ，τ，v]Τ中各元素估计精度的CRLB。

在第一个通道观测数据中引入相位ϕ1、时延td1和频移fd1等未知参数之后，对双通道时差、频差的估计性能可由式（28）计算获得。对该式求逆，得到参数集θ估计精度的CRLB矩阵为：

记M=C-1D(B-DΤC-1D)-1DΤC-1，显然该矩阵为正定矩阵。取e2=[0，1，0]Τ，e3=[0，0，1]Τ，则两种情况下对τ和v的估计精度的CRLB满足如下关系：

即相比于第二个通道的时延、频移参数估计结果，未知参数集θ1的引入降低了双通道信号时差和频差的估计精度。

类似地，如果在上两个小节的时差、频差估计性能分析过程中，保留未知参数集为ξ′=[a′Τ，θΤ2，θΤ]Τ，其中a′=[a2，a′]Τ，a′=a1/a2，θ2=[ϕ2，τ2，v2]Τ。则借助类似的分析，也可以证明双通道时差频差估计精度低于第一个通道的时延、频移参数估计精度。

5 仿真实验

本部分借助仿真实验验证论文所提出的时差频差估计方法的性能，以及已知信号波形条件下关于双站时频差估计性能的理论分析结果的正确性。仿真过程中通过改变观测站与辐射源之间的时差频差值、两通道接收信号的信噪比等参数来构造不同的场景，选取多次独立实验中得到的参数估计均方根误差作为性能评价指标，并在对应场景下比较了4 种时差频差精度，包括：①本文所提出的时差频差估计方法，估计值由式（10）最终给出；②基于互模糊函数（CAF）的传统方法［11-15］；③两通道累积误差，为两通道时延、频移值估计误差平方和的算术平方根，即，其 中M表 示统计仿真次数，上标(m)表示第m次仿真中对应参数的估计值，两通道的时差频差估计值分别由式（12）和式（13）给出；④时差频差估计精度的CRLB，通过对式（28）的Fisher信息矩阵求逆得到。

上述比较对象②中互模糊函数可看作一种近似最大似然方法，用于估计两站接收信号的时差频差，即

在具体实现过程中，通过遍历{τ，v}的可能取值范围，得到上式中互相关函数最大幅值对应的坐标即为，经线性变换可最终获得时差频差估计值

仿真实验中，假设两个观测站与辐射源之间的几何构型如图1所示，辐射源静止不动，两个观测站以不同速度沿水平方向高速运动，它们与辐射源之间的距离差异和相对径向速度差异造成了双站接收信号之间的时间差和频率差。假设入射信号采用BPSK 调制，信号带宽为200 kHz，信号持续时长为1.5 ms，信号原始波形先验已知，但该波形会在被两个观测站接收时因传播时延和多普勒频移等因素而产生变化。接收机采样率为1 MHz，每种场景下的统计仿真次数为500次。

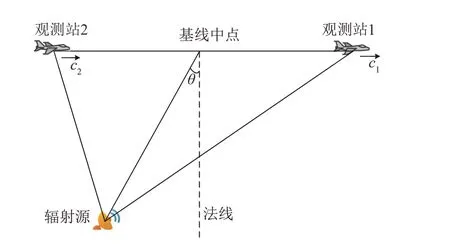
图1 观测站与辐射源的几何构型Fig.1 Geometric relationship between observation station and radiation source

首先，基于图1中描述的几何构型，进一步假设辐射源与两个观测站基线中点的斜距为15 km，两个观测站距离20 km，两个观测站分别以150 m/s 和250 m/s的速度沿水平方向运动，固定两个观测站接收信号的信噪比为-2 dB、时差和频差分别为7.12 μs和1 kHz，并假设两个观测站接收信号的信噪比相等且逐渐变化，得到不同方法的时差频差估计精度随信噪比的变化情况如图2所示。

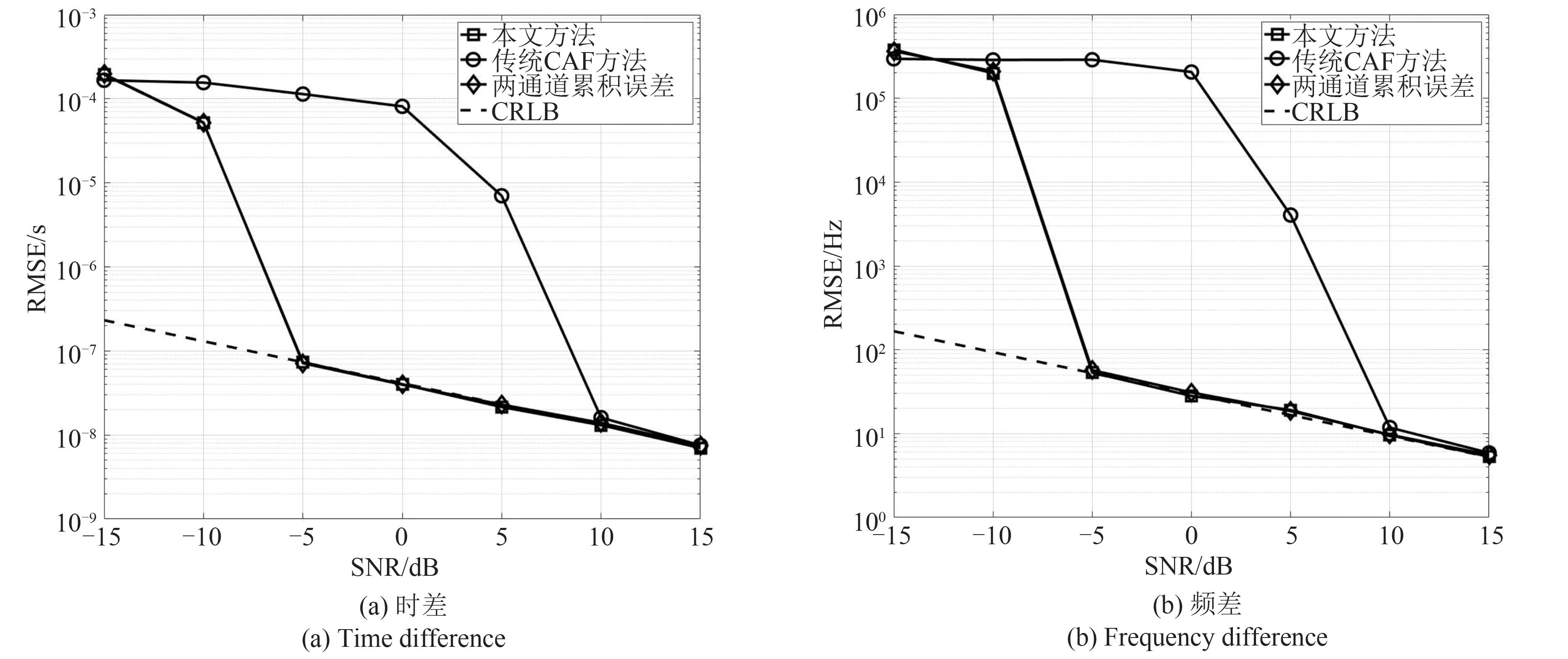
图2 两个观测站接收信号信噪比同步变化时的时差、频差估计精度Fig.2 Τime difference and frequency difference estimation accuracies when the signal-to-noise ratio of the signals received at two observation stations changes synchronously

图2 中的仿真结果表明，新方法借助对信号波形先验信息的利用，获得了显著优于传统CAF方法的时差频差估计精度。新方法在两个观测站接收信号低至-5 dB 时，就能够获得高精度的时差、频差估计结果，且随着信噪比的进一步升高，其参数估计性能与CRLB 十分吻合，且与两通道参数估计结果的累积误差基本一致，表明该方法是一种近似最优的估计方法，这些现象较好地验证了第四部分的理论分析结果。相比而言，传统CAF方法只有在信噪比升高至10 dB 左右时才能够实现对时差、频差的可靠估计，其信噪比适应能力与新方法相比有较大差距，这一差距说明了在时频差估计过程中对信号波形先验信息进行充分利用的重要性。

随后，在上一组仿真实验的基础上，固定第一个观测站接收信号的信噪比为0 dB，逐渐改变第二个观测站接收信号的信噪比，得到几种方法的时差、频差估计精度的变化情况如图3所示。

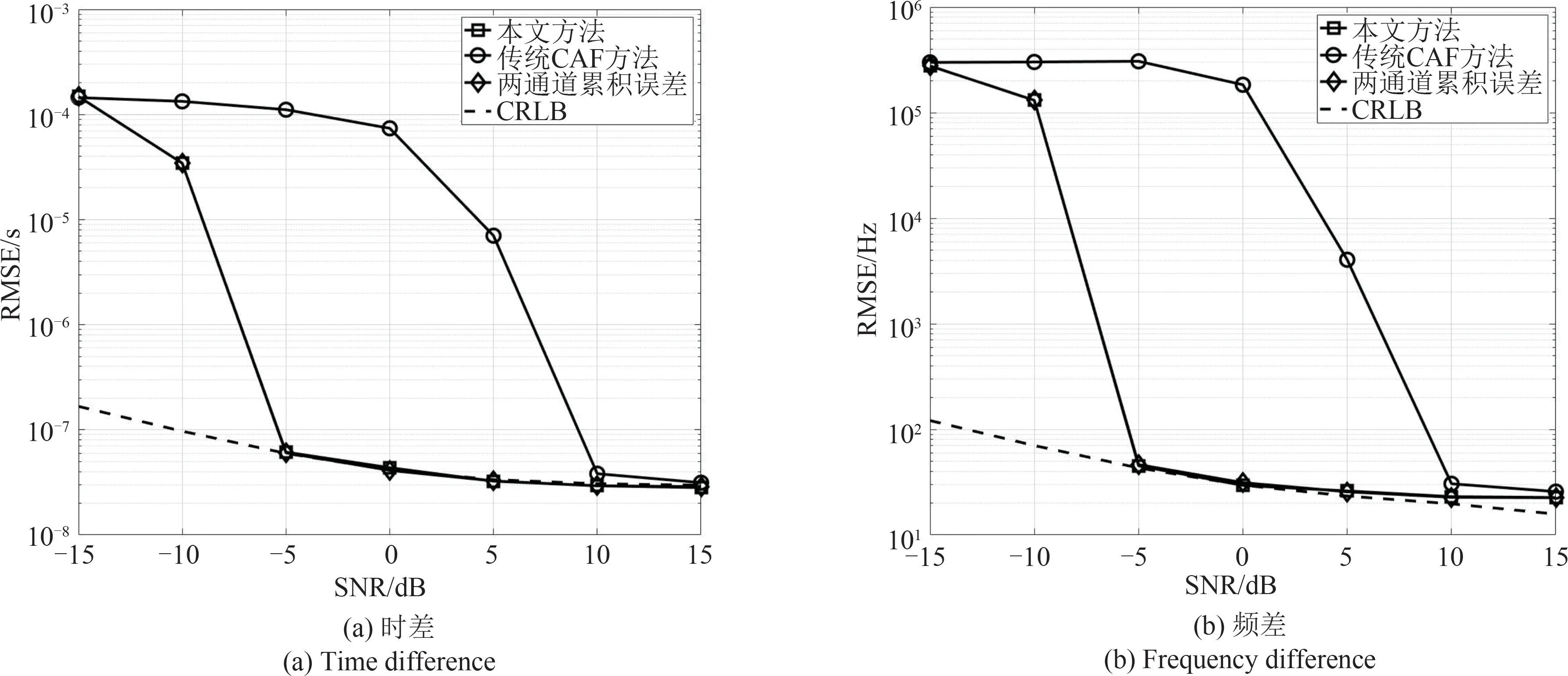
图3 单个观测站接收信号信噪比变化时的时差、频差估计精度Fig.3 Τime difference and frequency difference estimation accuracies when the signal-to-noise ratio of the signal received at a single observation station changes

图3中的仿真结果再次验证了新方法相比于传统CAF方法在信噪比适应能力方面的显著优势。与图2 中的结果类似，新方法和传统CAF 方法分别在第二个观测站的信噪比超过-5 dB和10 dB时达到收敛，新方法具有约15 dB的信噪比适应能力优势。进一步还可以看出，由于这一场景中两个观测站信噪比没有同步增大，图3和图2中的结果之间也存在一定区别。图3 中时频差估计精度的CRLB 和新方法的时频差估计均方根误差并没有随着第二个观测站接收信号的信噪比提高而呈对数线性规律减小，参数估计精度提高的速度更慢一些。对比式（28）中的Fisher信息矩阵和相应的CRLB表达式，尽管CRLBθ与单个观测站接收信号的功率成反比，但在单个观测站功率增大、另一个观测站功率保持不变的过程中，两个观测站的信号功率之比a2随之减小，给参数估计精度的提高带来了负面影响，最终减缓了参数估计精度的提高速度。当第二个观测站接收信号的信噪比超过0 dB 后，新方法的时频差估计精度与CRLB之间存在一定偏离，这也是由第一个观测站接收信号中较为显著的观测噪声造成的。

6 结论

本文针对观测站与辐射源之间存在相对运动的场景，充分利用信号波形先验信息提出了一种时差频差高精度估计方法，并理论推导了参数估计精度的CRLB，分析了时差频差估计精度与单通道时延、频移估计精度之间的关系。仿真实验结果表明，借助对信号波形先验信息的利用，新方法获得了比基于互模糊函数的传统时差频差估计方法更高的参数估计精度，以及对低信噪比等非理想信号环境的更强的适应能力。在所设定的信号环境中，新方法对低信噪比的适应能力比基于互模糊函数的传统方法增强了15 dB 左右。当新方法的参数估计性能达到收敛之后，其时差频差估计精度与CRLB非常吻合，且与两通道各自的时延、频移估计结果的累积误差一致，这些现象证明了本文理论分析结果的正确性。