基于室内试验水闸开度对水流特性影响分析
方晨蕾,葛晓伟,王 芳,董诗媛
(1.高邮市水利综合服务中心,江苏 高邮 225600;2.高邮市水利局临泽水利站,江苏 高邮 225600)
水闸是建在河道、渠道及水库、湖泊岸边具有挡水和泄水功能的低水头水工建筑物,对拦洪、挡潮、冲沙、取水或下游流量调节具有重要作用[1-3]。在水闸的水力参数设计中,流量设计十分重要,合理控制水闸开度不仅可以使水闸下游流量均匀分布,还可以防止两岸和河床的水土流失[4,5]。
孙海超[6]在理论上分析推导了起推水位偏差对水面线的影响范围,推算了闸下水位流量关系;迮振荣等[7]分析了影响平原河网地区感潮河段水闸下泄流量的成因,并通过成因分析研究了提高水闸流量控制方法;周全等[8]介绍了在线监测、水文水动力学模型、水力学及多元回归法过流公式3 种水闸流量计算方法,并计算了上海市浦东新区典型闸门流量过程;邢端生[9]以粤东某水闸为例,在分析流域产汇流特性基础上,分别用广东省综合单位法和平均排除法计算山区和平原面积的设计流量;孟健[10]以水闸不同启闭情况下的实测过闸流量为依据,结合水闸自身特性与水力学相关理论,探求可操作性的过闸流量推求方案;刘鹏等[11]对黄埔涌水闸正常和特殊设计工况过流流量进行了模型试验研究,分析了几种工况下闸门运行时开度与流量之间的关系。
本文通过水闸开度控制流量大小,采用Fluent数值模拟方法,引入能量耗散和流动阻力,分析对比了不同闸门开度下RNG k-ε、RNG k-ω 和RSM 湍流模型对流体速度分布和能量系数的影响,并通过室内水闸试验进行验证对比,研究结果可为相关工程提供参考。
1 室内试验装置
试验在国内某大学水力实验室水槽上进行,水槽为玻璃墙和钢底,尺寸为8 m×30 cm×50 cm(长×宽×深),水闸位于距离上游端4 m 处。流量由入口管上的闸门进行调节,通过放置在渠尾的V 形缺口堰进行测量。下游尾水深度由水槽尾部的闸门固定,有机玻璃门矩形门宽5 mm,采用精度为±0.5 mm的点式水位计测量水位。使用Nortek 的Vectrino 声学多普勒测速仪测量流速,输出采样频率为25 Hz,测量记录时间为40 s,通过分析平均瞬时数据计算湍流特性。试验装置,如图1所示。

图1 试验装置
2 数值模拟
2.1 计算方案
数值分析采用非稳态条件下雷诺平均Navier-Stockes 方程求解,可在70 s 的模拟时间内求出一个恒定的解,相比稳态计算,更具有时效性。计算时,采用SIMPLE 算法获得压力场,并采用PRESTO 框架将压力离散化,其他方程采用二阶离散格式,参数由Fluent Default 值给出。此外,湍流模型采用了3 种计算公式即RNG k-ε、RNG k-ω 和RSM,同时为了跟踪自由表面,使用了基于VOF 公式的流体体积模型。在整个计算域中,考虑了水和空气两相状态,流体的性质也被考虑在内,RANS 和连续性方程采用流体特性的体积分数平均值求解。
淹没流二维RANS模拟的域和边界条件,如图2所示。试验在淹没流中进行,总水头H0为0.3 m,闸门开度W为0.03~0.24 cm,下游水位h2为0.20~0.27 cm,相对闸门开度a=W/H0,淹没度s=h2/H0,x为闸门距离上下游的距离。

图2 淹没流二维RANS模拟的域和边界条件
2.2 数值网格
数值模型二维结构网格通过Gambit 生成,尺寸为6 m×0.4 m,闸门距离下游边界3 m 处为水平横坐标的原点。相对闸门开度a为0.1~0.8,创建了8 个不同的网格。网格在墙边界(底部和水闸)附近和自由表面区域被细化。构建网格是为了验证闸门到墙的无量纲距离在12<y+<250的范围内。
2.3 边界条件
边界条件和初始值,如图2 所示。水和空气在上游端以2 种速度条件分别注入,空气速度不敏感且等于零。假设水流速度呈指数分布,其公式为:
式中:U(y)为水流速度(m/s);γ为形状系数,根据从明渠中观察到的标准值取0.1;U0为进水口处的平均流速(m/s);y为水流垂直位置(m);h0为河道深度(m)。
第一次计算采用Garbrecht 流量方程确定流量和平均速度,以细化自由表面的网格,并在下游端固定静水压力出口。
3 结果分析
3.1 剖面速度分析
闸门小开口(a=0.2 和s=0.8,x=-5,-2,2,5,10)时的流速分布,如图3所示。
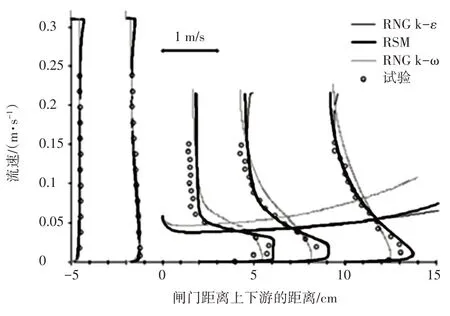
图3 闸门小开口时的流速分布
从图3可以看出,与室内试验结果对比,RSM 和RNG k-ε湍流模型能够很好地模拟出水流实际速度分布情况,而标准RNG k-ω 模型通常适用于射流模拟,在收缩射流上的模拟效果最差。
闸门大开口(a=0.7 和s=0.9,x=-1,-0.5,1,2,3)时的流速分布,如图4所示。
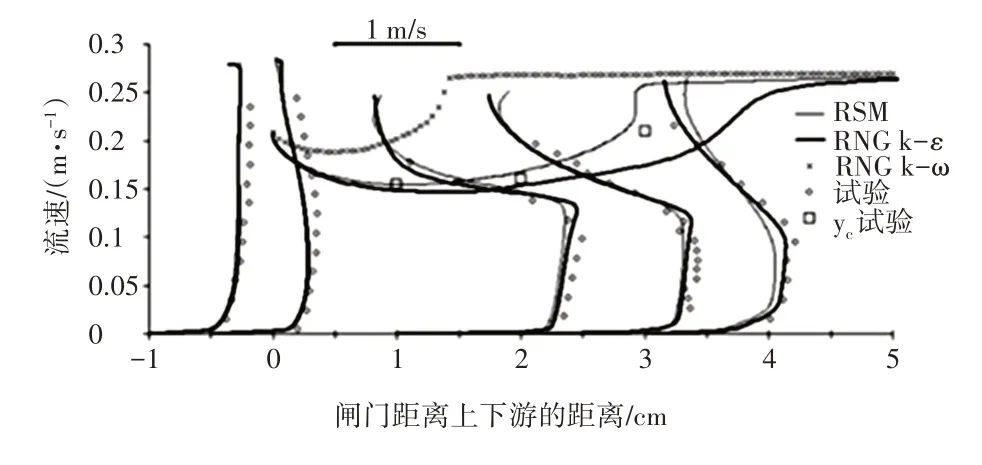
图4 闸门大开口时的流速分布
从图4 可以看出,在闸门大开度下,除闸门和收缩段之间存在射流外,所有RANS 模拟结果与试验一致。RSM 和RNG k-ε 湍流模型的结果非常相似,而RNG k-ω 模型计算出的结果与试验有很大偏差。在闸门上游,由于存在二维模拟未模拟出的再循环区,所以模拟出的纵向速度略低。模拟结果表明,靠近收缩截面的混合区域的流速略有增加,这与仅在x=1 处的试验相同,其误差可能是由于湍流模型和横向流速分布不均匀造成的。尽管如此,从试验和数值方法推导出的收缩系数非常接近,对于所有淹没比而言,小开口闸门的水流可以认为是射流,而大开口闸门下的流速分布在收缩断面中更不均匀。
3.2 能量修正系数分析
通过对流速的估计结果可以计算动能和动量系数。淹没条件s=0.9 时能量修正系数α变化规律,如图5所示。
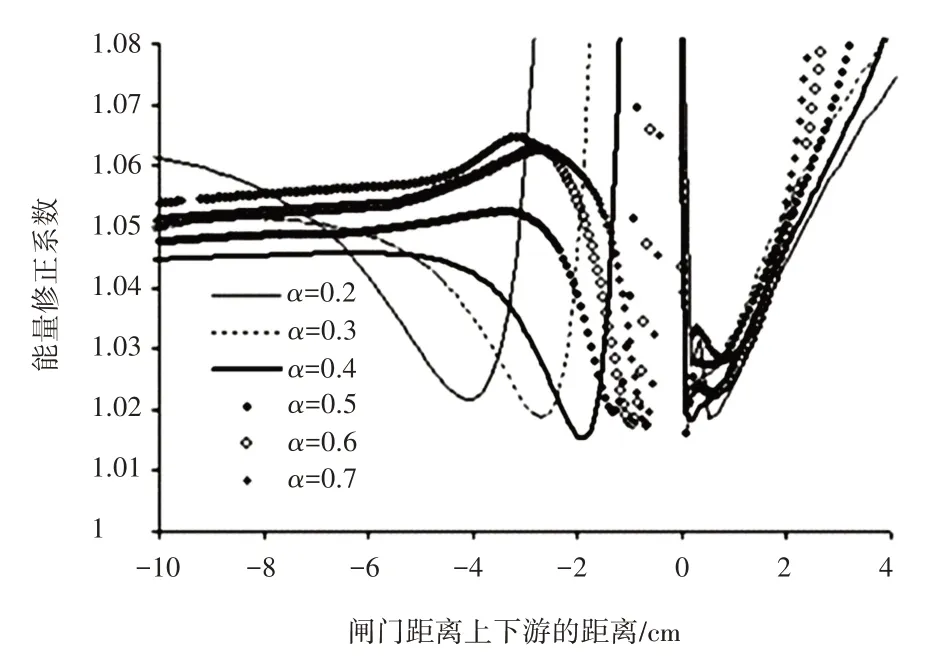
图5 s=0.9时能量修正系数α变化规律
从图5可以看出,α的最小值对应于纵向流速分布(边界层除外)最均匀处,同时与闸门开度有明显相关性,其大约为闸门开度的2~4倍。在下游部分,收缩段的α值在1.02~1.03,动量系数的平均值为1.02(闸门上游)和1.015(闸门下游)。上游水池和收缩段之间的水头损失约为总水头的1%,主要是由于边界层中的高流速梯度引起的。
4 结论
本文为分析不同水闸开度对水流特性的影响,采用Fluent 数值模拟方法,引入能量耗散和流动阻力,分析对比了不同闸门开度下RNG k-ε、RNG k-ω和RSM 湍流模型对流体速度分布和能量系数的影响,并通过室内水闸试验进行验证对比,结论如下。
(1)当闸门为小开口时,RSM 和RNG k-ε 湍流模型能够很好地模拟出水流实际速度分布情况,而标准RNG k-ω 模型通常适用于射流模拟,在收缩射流上的模拟效果最差。
(2)在闸门大开度下,除闸门和收缩段之间存在射流外,所有RANS 模拟结果与试验一致。RSM 和RNG k-ε 湍流模型的结果非常相似,而RNG k-ω 模型计算出的结果与试验有很大偏差。
(3)对于所有淹没比,小开口闸门的水流可以认为是射流,而大开口闸门下的流速分布在收缩断面中更不均匀。

