基于SOLO分类理论的新高考数学多选题的试题研究及建议

高 峰 戴晓娟

(宁夏师范学院数学与计算机科学学院,宁夏 固原 756000)

近年对于多选题的研究多为结构分析、解题研究等,很少根据思维层次来研究.鉴于此,本研究基于SOLO分类理论对新高考的多选题进行分析,旨在为教师教学提供参考.

1 研究设计

1.1 研究对象

本文选取2021、2022、2023年全国新高考Ⅰ和Ⅱ卷的多选题作为研究对象.

1.2 研究工具

SOLO意为“可观察的学习成果的结构”,是由澳大利亚心理学家比格斯和科利斯创建的一种描述个体在学习过程中的思维结构的框架.在此基础上形成的SOLO分类理论,是研究者根据个体的学习成果对其思维结构质性分类评价的理论[1].SOLO分类理论广泛应用于各个学科的研究,为教育教学研究带来新的视野[2].

1.3 层次水平划分

基于SOLO分类理论,针对高考多选题,编制SOLO层次划分.由于前结构思维的特征表现为思维逻辑混乱,难以理解题意,高考试题难以体现.故本文的层次划分不予以考虑.故将高考多选题的SOLO层次划分为单点结构(U)、多点结构(M)、关联结构(R)和拓展抽象结构(E).

2 研究结果及分析

确定试题的思维层次划分标准之后,对多选题进行划分,对可能会出现的矛盾或模糊的情况,做以下说明:

(1)若一题或某一选项存在一题多解,选择其中SOLO水平最低的那一水平;

(2)若使用排除法来解多选题,会影响水平层次的判断,故这里不考虑使用排除法来解题;

(3)介于两种结构中间的试题或选项,需综合考虑计算难度、背景熟悉程度等因素来判断层次水平[3-4].

2.1 分析举例

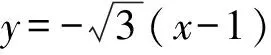
C.以MN为直径的圆与l相切

D.△OMN为等腰三角形

试题分析该试题以抛物线为情境,情景熟悉,考查对抛物线的知识点的掌握情况.选项A只需要掌握焦点与p的关系,故属于单点结构;选项B需要掌握求直线与抛物线的交点坐标和两点间距离公式,故属于多点结构;选项C需要掌握圆的知识以及直线与圆的位置关系,故属于多点结构;选项D需要掌握等腰三角形的定义以及两点间的距离公式,故属于多点结构.

例2(2023新高考Ⅱ卷12)在信道内传输0,1信号,信号的传输相互独立,发送0时,收到1的概率为α(0<α<1),收到0的概率为1-α;发送1时,收到0的概率为β(0<β<1),收到1的概率为1-β.考虑两种传输方案:单次传输和三次传输,单次传输是指每个信号只发送1次,三次传输是指每个信号重复发送3次,收到的信号需要译码,译码规则如下:单次传输时,收到的信号即为译码;三次传输时,收到的信号中出现次数多的即为译码(例如,若依次收到1,0,1,则译码为1)( ).

A.采用单次传输方案,若依次发送1,0,1,则依次收到1,0,1的概率为(1-α)(1-β)2

B.采用三次传输方案,若发送1,则依次收到1,0,1的概率为β(1-β)2

C.采用三次传输方案,若发送1,则译码为1的概率为β(1-β)2+(1-β)3

D.当0<α<0.5时,若发送0,则采用三次传输方案译码为0的概率大于采用单次传输方案译码为0的概率

试题分析该试题结合概率的知识,创设新颖且较为陌生的情境,考查对新定义的理解和应用.选项A需要理解单次传输的定义和不同情况的概率,故属于关联结构;选项B需要综合理解题目的全部内容,故属于关联结构;选项C需要综合理解并讨论译码为1时的不同情况,故属于拓展抽象结构;选项D需要深层次理解并比较不同传输方式下的概率,故属于拓展抽象结构.

2.2 试题多选题的SOLO思维层次的分析结果

根据划分标准确定多选题以及各选项的SOLO思维层次,得到如下结果,具体见表1、表2.

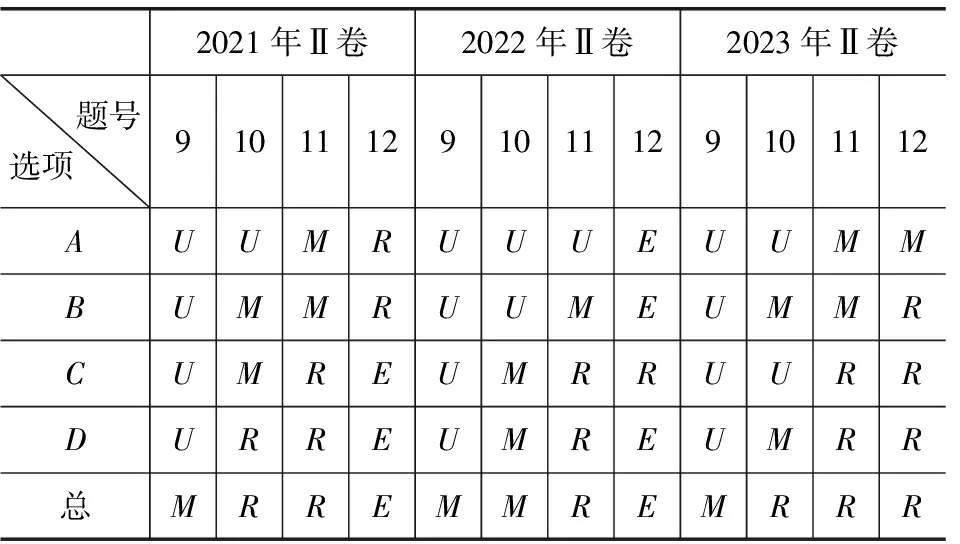
表1 2021-2023年全国新高考数学Ⅰ卷的多选题SOLO思维层次分布表

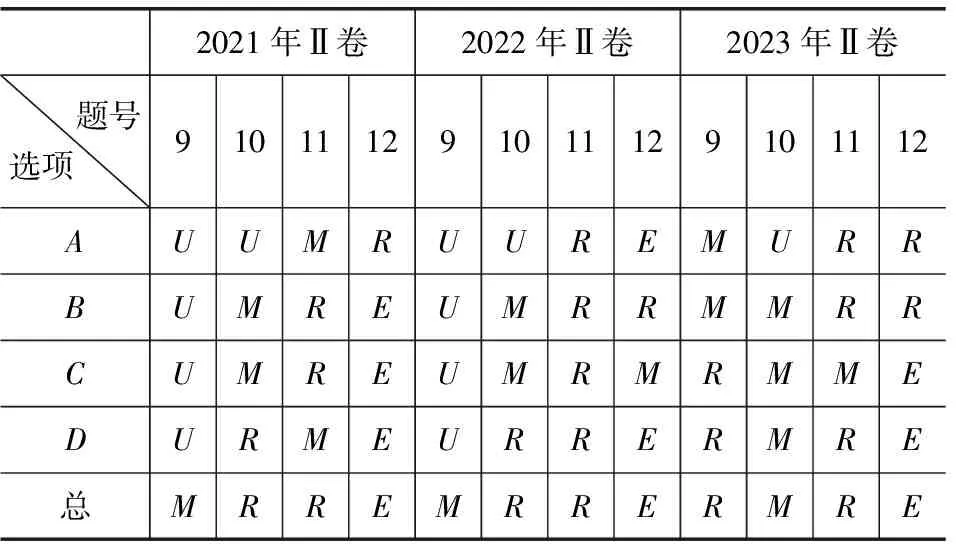
表2 2021-2023年全国新高考数学Ⅱ卷的多选题SOLO思维层次分布表

2.3 多选题整题的思维层次情况分析

整体来看,六套试卷的思维层次分布情况虽大体相似,但仍有差异.相似之处:除2023年Ⅰ卷,另五套试卷在多点结构、关联结构、拓展抽象结构上均有题目,并且随题号的增大,题目的思维层次水平也逐渐提高.9题多为多点结构,10和11题多为关联结构,12题以拓展抽象结构为主.

2021年Ⅰ卷和2021、2022、2023年Ⅱ卷思维层次相当,两道关联结构层次的题目,多点和拓展抽象结构各一道;2022年Ⅰ卷前两题为多点结构,关联和拓展抽象结构各一题;2023年Ⅰ卷有一道多点结构,三道关联结构,更强调基础知识和能力的考查,缺少拓展抽象结构层次,对更高思维层次的考查在其他题型中应该会加以补充.

2.4 选项的思维层次分布情况分析

六套试题多选题的各选项的思维层次分布情况与题号的大小联系紧密,随着题号的增大,思维层次较高的选项占比增加.第9题的选项多为单点结构,保证对基础知识的考查;第10题以单点和多点结构为主,偶有关联结构;第11题以多点和关联结构为主;第12题以关联和拓展抽象结构为主.当一道题有不同层次水平的选项时,层次水平基本按照选项的顺序递增.层次分布与给分规则相结合,让各个层次的学生在各个题上都有发挥空间.

除2023年Ⅰ卷以外,多选题的16个选项在四个层次上均有分布,但占比不同.六套试卷的较低水平选项,即单点结构和多点结构,共计占所有选项的一半左右,且Ⅰ卷相较Ⅱ卷比例更高,更注重基础题型和知识点的考查.在关联结构方面,六套试卷的占比差别较大;拓展抽象结构的选项数量差别不大,除2023年Ⅰ卷外,多为2个或3个,反映出多选题中较难选项数量较少且稳定.

3 思考与建议

3.1 注重多选题SOLO思维层次分布的全面性和均衡性

部分试卷的多选题中缺失存在某一思维层次,例如2023年Ⅰ卷多选题缺少拓展抽象结构层次的试题;或者层次分布有失衡现象,例如2022年Ⅰ卷的多点结构的选项占比较大.为使多选题的结构更优化合理,各种思维层次的题目和选项应尽可能涵盖且合理分配份额,以发挥多选题的作用效果.

3.2 关注高阶思维试题或选项的命制

根据统计,试卷对拓展抽象水平的考查比例均较低,对学生高水平思维的关注度需有待提高.因此,Ⅱ卷继续保持对思维层次的考查,Ⅰ卷可适度增设更具度和广度的题目和选项.

3.3 对高中多选题教学的建议

3.3.1构建认知结构体系

教师和学生应注重理解知识之间的联系性,构建知识结构体系,这是解决关联和拓展抽象结构的基石.为辅助思维上知识体系的构建,可以利用思维导图、思维图谱等[5],形成和强化知识的关联点和拓展点,形成整体思想.

3.3.2发展创新意识与能力

多选题的12题以拓展抽象结构为主,情景新颖、真实且复杂,这不仅提升试题结构层次,而且也给学生带来了题目阅读量大、新信息多的挑战.学生需要面对陌生问题,联系旧知,大胆猜想和探索的思维和能力.因此教师需要提升自身的数学和教学素养,更好地在课堂教学和解题训练中培养学生的创新精神[6].

3.3.3关注差异,因材施教

多选题以其丰富的结构水平兼顾了多层次思维的考查,更加关注个体差异,强调以人为本的理念.教学中,教师要充分考虑和兼顾不同思维水平学生的“最近发展区”,课堂提问和作业布置要体现梯度性和层次感,既能激发数学学习的热情、搭建基础性知识体系,又能启发和锻炼思维的灵活性和开放性.

4 结束语

SOLO分类理论能够对多选题及选项进行分层研究,分析学生思维的深度和广度,为教学提供理论研究的依据,有利于多选题的教学研究和命制研究.