一题多想 培养高中学生的发散性思维

姚 新

(黑河市第一中学,黑龙江 黑河 164300)

教师不仅要关注做题的结果,更要关注做题的过程,关注发散性思维的发展过程.一题多想能提升学生多方面的能力,如数学建模能力、独立思考能力、提出问题的能力以及实践探索的能力.

1 引导学生思考有没有新的问题

对于高中数学学习而言,教师不仅要关注学生回答问题的能力,同时也要关注学生提出问题的能力.当学生在解决一道题设定的问题之后,教师不要让学生转战另外一道题,而是要让他们思考,能不能基于原题的条件与刚揭示的结论去发现新的问题.这其实就是培养学生的发散性思维,让他们从原先的问题出发去思考新的问题.

以下面这题为例,如图1所示,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC⊥BC,AC=BC=2,CC1=3,点D、E分别在棱AA1和棱CC1上,且AD=1,CE=2,M为棱A1B1的中点.求证:C1M⊥B1D.

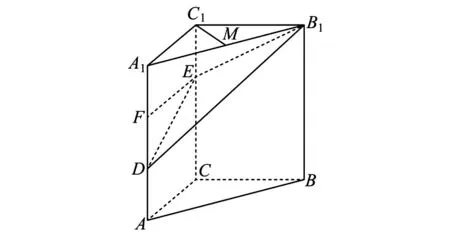
图1 三棱柱ABC-A1B1C1

对于这题,学生可正面思考,只要证明出C1M⊥平面AA1B1B,即可证得C1M⊥B1D.在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,则BB1⊥平面A1B1C1.因为C1M⊂平面A1B1C1,则C1M⊥BB1.因为AC=BC,∴A1C1=B1C1,∵M为A1B1的中点,∴C1M⊥A1B1.又因为BB1∩A1B1=B1,∴C1M⊥平面AA1B1B.又∵B1D⊂平面AA1B1B,∴C1M⊥B1D.

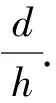
培养学生发散性思维的前提是将学生视为课堂的主体,要给他们更多思考的时间与空间.当学生思考有没有新的问题时,自然要跳出固定思维模式,尝试去从不同的角度看待问题,发散性思维的火花就会不断迸发.

2 引导学生思考有没有新的解法

大多时候,教师设置的题目只有唯一的解,这其实容易桎梏学生的思维.教师可改变出题的方式,多给学生一些开放性题,学生做完一道题后,教师可问他们能不能想到新的解法,以激励他们运用不同的知识点,解决相同的问题,以让他们的思维从一个领域发散到另外一个领域.

在教学中,教师激励学生对同一问题采用不同的解法,这能提升学生的发散性思维,培养他们多元化的思考方式,进一步拓展学生的思维发展空间.促使他们在学习中更加主动、积极地探索和发现问题的答案[1].

3 引导学上思考有没有类似题目

教师要提升学生综合运用知识的能力,就需要引发学生在完成解题任务后还要思考相关的问题,以形成一定的知识脉络,以在发散思维中形成结构化认知.

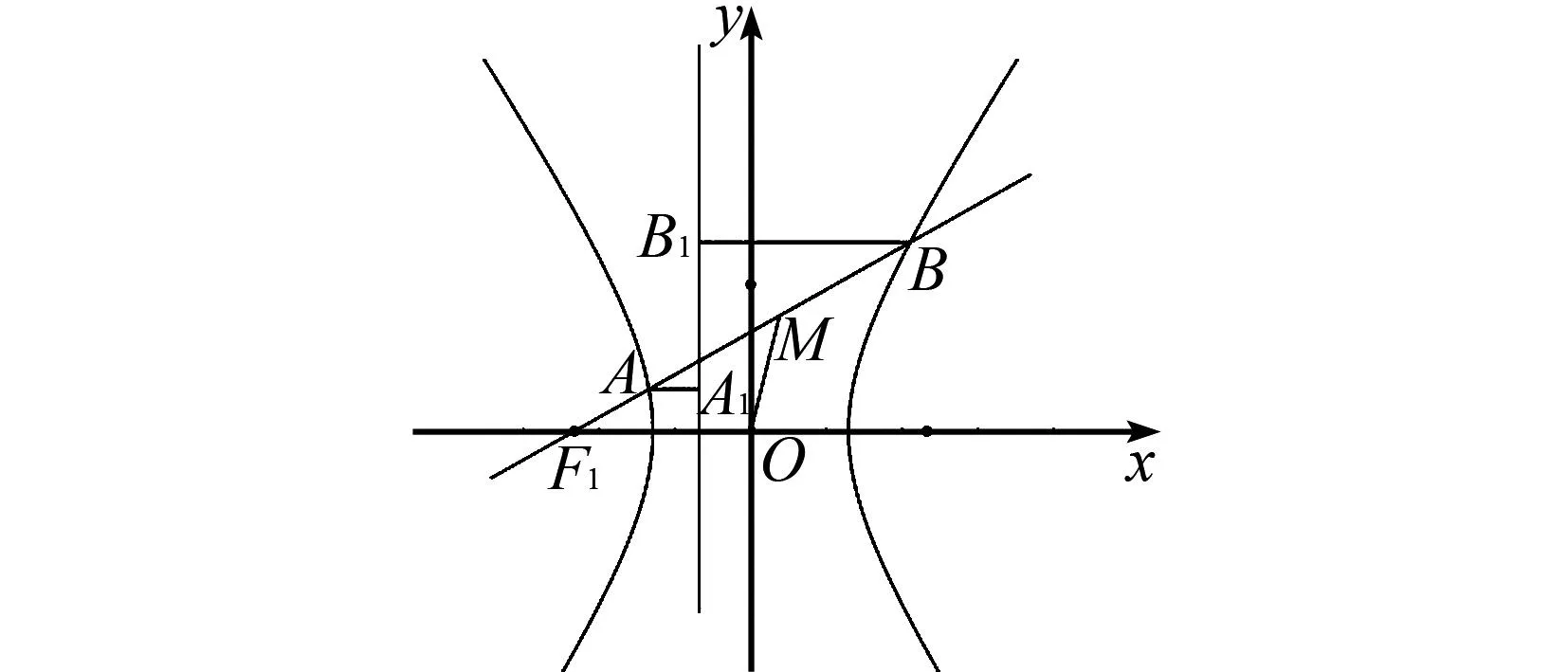
图2 双曲线

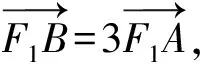
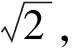
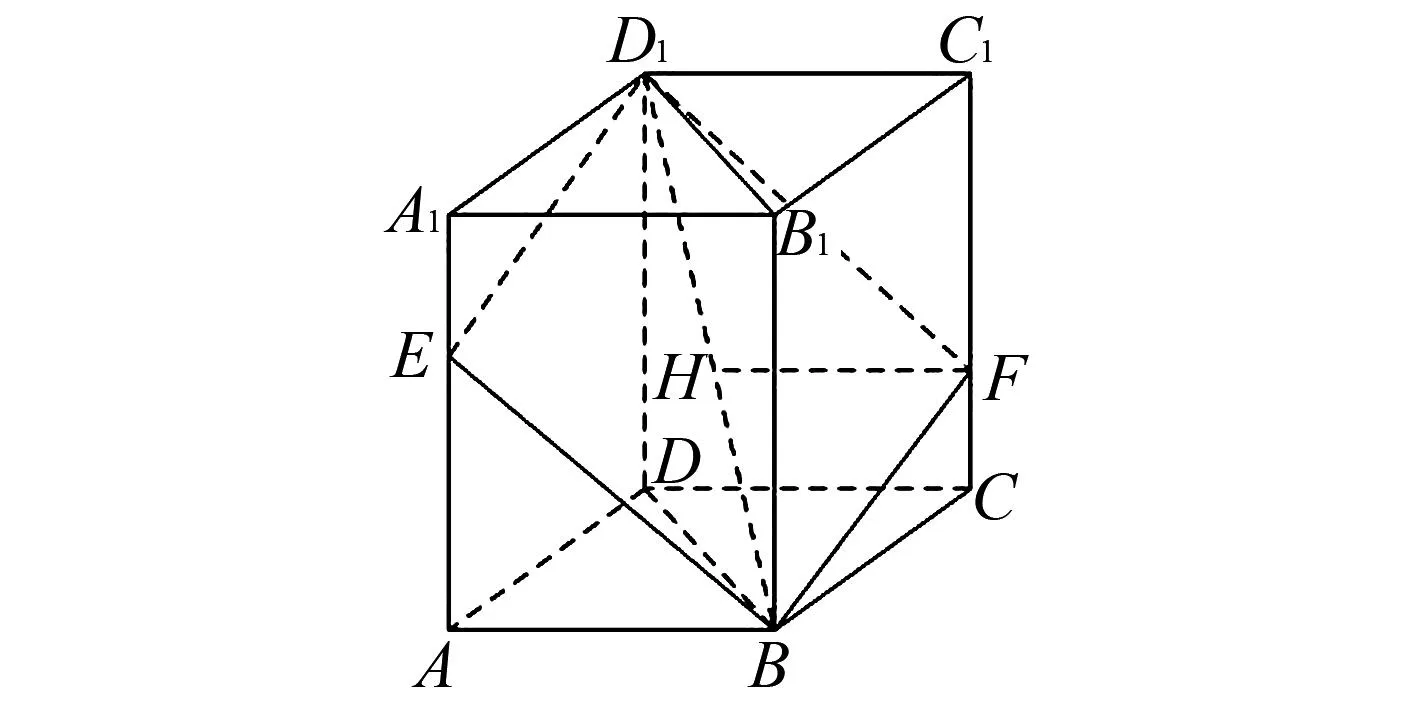
图3 长方体ABCD-A1B1C1D1

学生先是借助刚才解题的经验,根据题目画出图形,再运用数形结合的方式解题.

4 引导学生反思相关的错题经历

教师在培养学生的发散性思维时,既需要他们结合现学的认知,也需要他们融入之前所学的内容;既需要他们考虑当下的解决问题的方案,也需要他们思考过去的错题经历.

以下面这题为例,羽毛球运动是一项全民喜爱的体育运动,标准的羽毛球由16根羽毛固定在球托上,测得每根羽毛在球托之外的长为7 cm,球托之外由羽毛围成的部分可看成一个圆台的侧面,测得顶端所围成圆的直径是6 cm,底部所围成圆的直径是2 cm,据此可估算得球托之外羽毛所在的曲面的展开图的圆心角为多少?

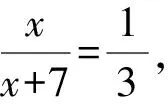
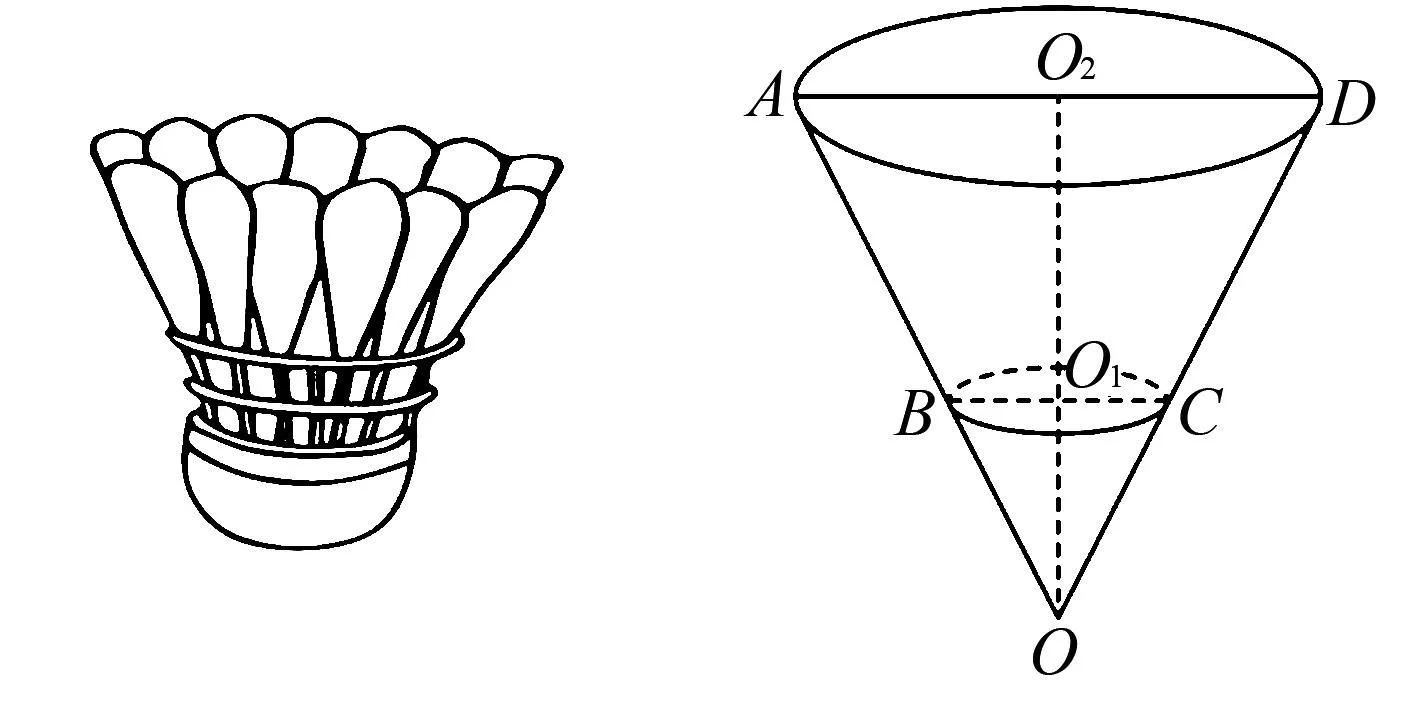
图4 标准羽毛球示意图

引导学生反思相关的错题经历是一种培养学生发散性思维的重要方法.通过这样的引导,教师可以帮助学生更好地反思自己的学习经历和错误,并从中总结经验教训,形成更加全面、深刻的知识体系和发散性思维方式.

5 结束语

在一题多想的过程中,教师需要引导学生从不同的角度来考虑问题,从而提高思维的灵活性和创造性.