基于新高考的数学教学策略探究

王阿娟

(安徽省亳州市利辛县利辛高级中学,安徽 亳州 236708)

在新课程改革的背景下,高考数学卷中的试题也出现了新的变化.一方面加强了对基础知识的考查,另一方面在命题趋势上发生了转变.对于学生的解题能力提出了更高的要求,数学教学的方式和思路也要随之变化.

1 梳理高考考点,分析数学命题趋势

在高中备考过程中,高考发挥着导向性的作用,教师必须明确高考考点,才能有效地确立备考的内容与目标,引导学生了解高考命题的特点和趋势,并提前做好练习和准备,提升教学的效果.从近年的高考数学试卷内容来看,“文化育人”的趋势越来越明显,许多题目都会以历史文化、民俗文化、科技文化为背景[1].

例1(2020·新高考Ⅰ卷)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( ).

图1 例1题图

A.20° B.40° C.50° D.90°

这类问题有着一定的文化内涵,文化信息与数量关系相互交融,对学生的数学阅读理解能力提出了较高的要求.在讲解这道题目的时候,教师可先向学生介绍日晷的结构与作用,然后引导他们画出截面图,根据面的平行性质和线面垂直定理判断截线的关系,根据点A的纬度,计算出晷针与点A处水平面形成的角,即40°.这道题目的运算过程并不复杂,但有些学生不知道什么是日晷,在解题中产生了错误.由此可见,高中数学教师不仅要教授给学生数学知识,还要加强文化素养层面的教育,在日常教学中渗透文化知识,拓展学生的学习视野.

2 把握知识关联,培养综合解题能力

在新高考改革的背景下,数学命题向着综合性的方向发展,一道题目可能同时涉及多个单元的知识点,对于学生的综合思维能力与知识应用能力提出了较高的要求.因此,高中数学教师不能将各个单元看作独立的部分,而是要打破单元之间的界限,让学生能够将所学的知识整合起来,加强对学生综合解题能力的培养.

例如在复习《充分条件、必要条件的判定》的时候,教师可设计如下题目:

例2(2021·全国甲卷)等比数列{an}的公比为q,前n项和为Sn.设甲:q>0,乙:{Sn}是递增数列,则( ).

A.甲是乙的充分条件但不是必要条件

B.甲是乙的必要条件但不是充分条件

C.甲是乙的充要条件

D.甲既不是乙的充分条件也不是乙的必要条件

通过这道题目的教学,既能够深化学生对充分条件、必要条件概念的认识,也能够帮助学生温习关于数列的知识点,锻炼学生综合分析与解决问题的能力.

3 复习概念原理,奠定数学知识基础

新高考十分注重对基础知识的考查,包括基本的数学概念、性质以及通项公式等,相关试题的难度并不高,学生只要牢固地掌握关于数列的基础知识,即可得出正确答案.数学概念是数学课程的基础部分,如果学生对概念理解不清,就很难掌握相关的公式、发展和定律,更无法解决实际的问题.有些学生对数学概念的内涵与外延认知不清,结果在做题时出现了错误.在复习备考的时候,许多教师比较重视对学生解题能力的训练,对基础知识的重视程度不高,结果导致学生对数学概念、原理的理解不到位,在解题过程中出现了一些简单的错误,导致丢分.因此,高中数学教师在备考过程中,要及时引导学生复习基本概念,帮助他们奠定知识基础[2].

例3 (2021·甲卷)已知数列{an}的各项均为正数,记Sn为{an}的前n项和,从下面①②③中选取两个作为条件,证明另外一个成立．

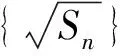
注:若选择不同的组合分别解答,则按第一个解答计分．

该类型的题目在高考试卷和模拟试卷中都比较常见,问题的本质是对等差或等比数列性质的证明,通常需要与运用相应的通项公式来解答,有时还会涉及变换公式.许多题目还可以采用二元一次方程的方式进行解答.此外,还有一些高考题目要求学生证明数列成等差或等比关系,这类题目一般可以运用数列的定义进行判断和作答,或者也可以运用等差中项、前n项和等方式解答.

4 解析高考题型,教授答题技巧方法

高考数学试卷包括选择题、填空题、解答题等多种题型,演变出来的题目也比较复杂,对于学生的思维能力要求较高.学生要在整体分析题干的基础上,理解题目的类型与本质,然后选择最为恰当的方式求解.数学教师要对高考数学试卷中的题型进行归纳分析,从中总结不同的解题技巧,对题目进行分类,并指导学生掌握多元化的解题方法,使他们能够根据具体的问题,运用恰当的方式进行作答[3].

以填空题为例,填空题介于选择题与解答题之间,是一种只写结果、不写过程的客观性试题,多以定量型的问题出现.教师可教授给学生多种解答填空题的方法,让学生根据具体的题目,选择最恰当的方式来作答.

一是直接法,根据题目给出的条件,结合相关的数学公式、原理等,通过推理和计算直接得出结果,这是解答填空题最简便、最常用的方法.

二是数形结合法,数形结合是解题中常用的思想方法之一,教师可让学生通过画图的方式,将题目中的数量关系直观地呈现出来.

例4若圆x2+y2=r2(r>0)上恒有4个点到直线l:x-y-2=0的距离为1,则实数r的取值范围是____.

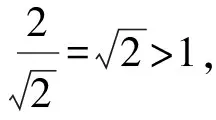
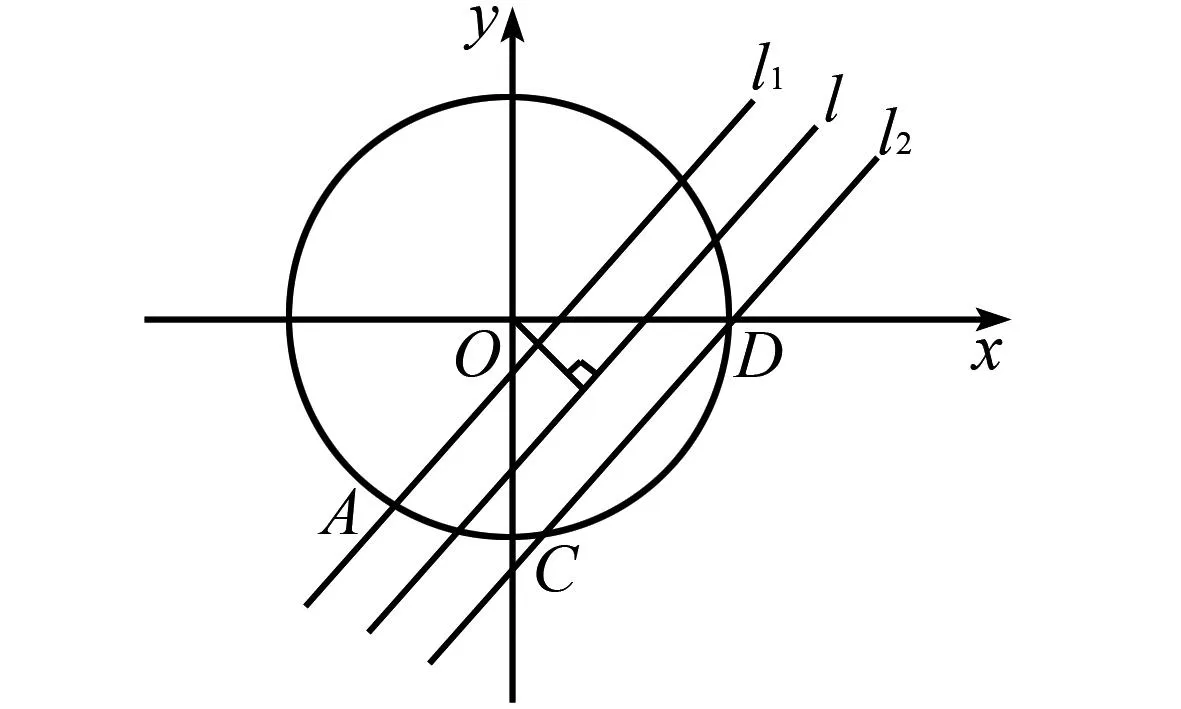
图2 例2题解析示意图

此外,构造法、等价转化法也是解答填空题时常用的方法.教师可通过例题讲解、专题分析等方式,引导学生深入理解一类题型的特点,掌握对应的解答方法和技巧,从而提升学生解答题目的效率和正确率.

5 抓好习题训练,总结数学解题思路

习题训练是高中数学教学的重要环节,也是提升学生解题能力的有效途径.教师可以通过组织专题训练活动的方式,锻炼学生对所学知识的应用公能力,使他们在解答实际问题的过程中,加深对所学知识的理解.要注意的是,习题训练与题海战术并不相同.在传统的高中数学教学中,有些教师会布置大量的习题,让学生进行重复、机械式的练习,教学效果不够理想,反而导致学生产生了很大的学习压力.在专题训练活动中,教师要注重习题的质量而非数量,可围绕高考考点选择一些具有代表性的题目,指导学生进行思考与解答,做到“精讲精练”,力求通过一两道典型习题,让学生掌握这类题目的解题思路.

以数列求和问题为例,一些比较简单的题目可以直接运用等比、等差数列公式进行求和,但在高考试卷当中,数列求和类题目大多都需要运用特定的技巧和方法.

(1)证明:数列{bn}是等差数列;

(2)求{an}的通项公式．

这道题综合性就非常强,需要学生深刻理解数列的递推关系.数学教师首先要做好基础性的习题训练,让学生理解并能够熟练运用公式法求和.然后再教授给学生一些其他的数列求和方法,如错位相减法、拆项求和法等.引导学生学习这些方法的定义,开展习题训练活动,巩固学生对各种求和方法的应用能力.

6 运用错题资源,不断提升答题水平

在数学学习过程中,犯错是难免的.有些学生对错误存在不当的认知,一旦发现自己出错就感到紧张、焦虑、恐惧,想要逃避自己的错误.高中数学教师要引导学生树立正确的学习观念,让他们正确地看待错误、面对错误,把错误当成自己不断进步的解题.错题反映了学生在知识基础、解题习惯、逻辑思维等方面的漏洞与不足,是宝贵的教学资源,教师要将学生在日常测验、作业中的错误资源整合起来,针对学生的错误进行深入分析与讲解,帮助学生查漏补缺,完善数学知识结构[4].

有些教师仅针对错题本身进行讲解,没有深入挖掘学生出错的原因,以至于学生对自己的错误没有形成深刻的认识,在后续的作业、测验中仍会出现相似的错误.因此,高中数学教师不仅要为学生提供正确答案,还要引导学生分析错因,找出错题背后蕴含的知识点.

7 结束语

高中数学教师要紧跟新高考的发展步伐,了解高考的新动向、新趋势,分析新高考对于学生发展的要求.据此确定教学的目标和策略,引导学生构建完善的数学知识体系,促进学生思维能力、问题解决能力等多方面的发展,为学生未来的学习与发展奠定坚实的基础.