核心素养视角下高中数学建模的教学实践研究

杨晓芳

(常州市北郊高级中学,江苏 常州 213000)

数学建模是沟通现实世界与数学领域的重要桥梁,更是高中阶段重要的教学内容之一,它能够启迪学生解决问题的思路,使学生实现从“盲目无知”到“自我认知”的转变.高中阶段要重视数学建模教学内容,结合实际的考情、教情与学情,发展学生的数学核心素养,落实数学建模育人目标[1].

1 激发兴趣,结合生活调动学生建模意愿

皮亚杰曾说过:“所有智力方面的工作都要依赖于兴趣.”数学建模与生活紧密相连,这更有利于激发学生学习数学的兴趣,为学生认知数学建模、学习数学建模增强引导与提供动力.数学概念高度抽象,不便于学生理解,课堂相对就显得枯燥,即便是高中生,其课堂学习的注意力也很难保持长时间集中.因此,教师要梳理数学概念中的变量关系,结合学生的实际生活,再联系学生的当前的认知水平,将实际生活变成数学问题抛给学生,引导帮助学生运用课堂所学的数学知识,建立模型去解决身边的实际问题.边学习,边建模,边应用,在问题解决的过程中感受数学的独特魅力与学习意义,激发学生“我想学”的兴趣与“我要学”的意愿,让学生在兴趣的带动下始终保持数学学习的主动性与积极性.

如,现在一些农商为了增加蔬菜的产量,让蔬菜有个好看的外观,都会打很多的药物助力蔬菜生长,即使多次清洗,仍会有药物残留.我们要如何用一定量的水去清洗蔬菜,才能安心食用呢?笔者将这一问题抛出后,学生七嘴八舌地发表意见,有的说要清洗两次,有的说要清洗不少于三次.笔者引领学生建立数学模型去分析问题,解决问题.

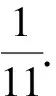
2 立足教材,精选案例启迪学生建模思想

“数学建模”是数学学科核心素养之一,在高中教材中主要有两方面的作用.一方面,是用函数模型来反映现实中的常见问题[2];另一方面,是通过数学模型创设情境,引导新的教学内容.课本教材中的案例存在普遍的共性问题,就是被精心加工过,优化了条件与过程,重点放在各个变量之间的逻辑关系,结构良好,数学性强.但弱化了真实情境的假设,偏离了学生实际生活,生活性弱,学生体验感不强.

与此同时,发展学生核心素养的教学与启迪学生思想的教学并没有本质上的区别.如,现实生活中“1”并不存在,我们需要假借生活真切存在的事物,一斤水,一筐蔬菜等才会感知“1”的存在.因此,数学建模也要有迹可循,结合具体事情的具体问题引导学生,才会让学生感受到抽象的数学概念.因此,在学生初学数学建模时,教师要精选生活案例,立足考情、教情与学情,按着建模的基本步骤,引导学生认识数学建模、学习数学建模,让学生感受数学建模在现实世界的重要意义,鼓舞学生学习与应用数学建模的动力,帮助学生知识迁移,建立起严谨的数学思维逻辑.

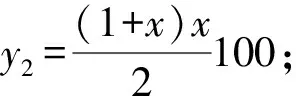
笔者通过背景分析、模型分析、建立模型、解决问题四个步骤,将生活问题转化为数学模型,呈现了用数学符号与语言解决生活问题的全部过程,让学生真切感受到数学模型在生活中的重要性.

3 分门别类,数学模型分类形成系统认知

孔子曰:“学而不思则罔.”任何知识的学习,都是在大量的吸收后进行归纳与总结,找到知识一般性的规律,进而了解知识的本质特征,加快知识学习的速度与实际应用迁移能力.因此,在高中数学模型教学中,教师要帮助与引导学生能够对各类数学模型进行有效的分类,掌握数学模型的一般性规律.以建模的思维去思考问题,以建模的能力去解决问题,使学生的数学建模能力得到切实的提高.

高中教学中的数学模型涵盖面较浅,依照模型所使用的数学工具来分,大致可以分为:函数模型、几何模型、复数模型、三角模型等.由于高中数学模型是优化后较为理想的模型,与实际中的数学建模还存在一定的差异性,因此,教师在教学中除了教授学生构造数学模型去解决实际生活问题外,还应该引导学生利用数学建模的思想,来解决理论性的“纯”数学问题.一方面,提高学生的解题能力,使学生的数学成绩有一个质的飞跃;另一方面,让学生熟知数学建模的一般性过程,使学生逐渐形成数学建模的表达能力、应用能力、逻辑能力及数学与生活的连接能力,真切将数学知识应用到生活之中,用建模思维去解决生活中遇到的各类难题,使学生的数学核心素养得以发展[3].

上述问题就是“纯”数学问题,学生通过建立数学模型,能够使复杂的问题浅显化,启迪解题思路,从而解决问题.而这些就需要学生在脑海中有完善的数学知识结构,知道这个问题属于哪一类,用哪一种方式去解决.这是学生熟知各类数学模型后,将不同概念、性质的知识在脑海中产生联结,举一反三、触类旁通的结果.因此,教师在教学中,帮助与引导学生对数学模型进行分类是十分有必要,也是十分重要的教学内容.这能够使学生在遇到问题后,明确解决问题的方法与手段,也能够使学生将各种数学知识融会贯通,熟练掌握与使用,即让学生用建模去解决问题,也使学生具备建模化的思维逻辑.

4 多元教学,基于教情开展多样教学形式

数学建模课与其他数学知识授课有很大的不同.因为数学是极度抽象的形式学科,有特定的数学语言、符号、定理、公式等,是虚无缥缈的“理论研究”,因此实践性较差.而数学建模课,就是用“模型”将现实世界与理论研究连接起来,让学生在实践中经历用数学建模去解决实际问题的过程,将学生已学过的知识、已具备的数学能力调动起来,进而培养学生缜密的数学思维和严谨的数学逻辑.因此,数学建模课更需要学生积极、主动地参与进来,教师引导为主,开设多样的教学形式来调动学生的学习热情[4].

其一,结合一般教学形式,找准数学建模课的“切入点”.数学建模课与其他数学知识授课存在着一定的联系,教师在其他数学知识授课中,如概念课、复习课、讲评课等,讲到与数学建模联系紧密的知识点时,可以无声渗透数学建模知识.一方面,可以加深学生对数学建模的理解与认知,强化学生数学模型的应用意识;另一方面,纯粹的数学建模课学时有限,可以缓解“内容多,课时少”的教学压力.

其二,学情导向教学形式,攻克学生学习建模的“困难点”.多数教师在数学建模课中只讲授建模与求解这两个环节,简化数学建模的问题分析、条件及模型检验等环节.但学情不同,学生对于建模各环节的掌握情况也不尽相同.同时,不同的教学内容、各数学建模步骤的重要程度也不尽相同.因此,教师应找准数学建模课的重点与难点,结合学情需要具体分析.

其三,欣赏学习教学形式,带领学生学习优秀建模案例.高中阶段的数学知识较浅,数学模型也就有着很大的局限性,距离真正意义上的数学建模有着一定的差距.尽管如此,学生高考之中可能用不到这样的数学建模知识,但教师也十分有必要让学生了解数学建模的真实面,带领学生了解更为复杂的数学模型案例.如国家年度粮食产量预测、长江水流量预测、大学排名问题、交巡警服务平台的设置与调度问题等,开阔学生的眼界,提高学生的认知,真正用建模贯通“数学”与“生活”的桥梁,体现数学的价值,让学生对数学学科有更高层次的认识、更深层次的热爱.

5 结束语

教师要基于学情,以学生的情趣为出发点,调动学生学习数学建模的热情;基于教情,精选并优化教材中的案例,启迪学生数学建模的思想;基于考情,帮助与引导学生对数学模型进行分类;再基于数学建模课的特点,开展多样的教学形式,切实提高学生的数学建模能力,使学生的数学核心素养得以发展.