能量守恒定律在高中物理解题中的应用研究

傅 祥

(扬州市广陵区红桥高级中学,江苏 扬州 225108)

高中物理学习中,能量守恒是解决问题的重要思维工具.教师在教学中,应注重示范和引导学生将能量守恒定律应用于具体问题,并着力培养学习者的解题技巧与实际运用能力.

1 能量守恒定律的内涵

能量守恒定律是自然科学中的基本原理之一,它阐述了在一个封闭系统内,能量的总量在任何时刻都保持不变的规律.这一定律表达了能量在系统内部的转换和变化,但总能量始终保持恒定.简言之,能量不会被创造或毁灭,只会在不同形式之间转化,但总量保持恒定.这一规律核心在于系统与外部隔离,没有能量或物质交换.

能量守恒定律在各种物理现象和系统中都有应用,不仅适用于经典力学范畴,也适用于现代物理学和量子力学.这一定律在科学、技术和工程中扮演着重要角色,影响着能源利用、环境保护等方面的研究和实践[1].

2 不同形式的能量之间的转换和守恒关系

不同形式的能量之间存在着一种持续的转化和守恒关系,如动能、势能、热能、化学能等.动能代表着物体由于其运动而具有的能量,而势能则源自于物体的位置或状态.在自然界中,这两种能量形式经常相互转换.同时,热能也在能量转化中扮演重要角色,它是由于物质内部分子或原子的运动和振动所产生的能量.在许多情况下,机械能会因为摩擦而转化为热能,这样的转换会导致系统温度的升高.化学能是存在于化学反应中的一种形式能量.它能够转化为其他形式的能量,比如电能、光能等.典型的例子是电池,其中的化学能可以转化为电能,为电子设备提供能量[2].

尽管能量可以以各种形式相互转换,但总能量在一个封闭系统中始终保持不变.这一基本原则贯穿着自然界中各种现象和技术应用,为能量转换和利用提供了重要的理论支持.

3 能量守恒定律在物理解题中的应用途径

3.1 能量守恒在弹簧问题当中的应用

弹簧不仅仅具有弹力,还可以储存和释放能量,当弹簧受到压缩或拉伸时,能量的转换成为关键的考虑因素.这时势能与动能之间发生着转换,从而体现能量的守恒.例如,当拉伸弹簧时,因形变而储存的势能会随拉伸程度增加而增加,当弹簧恢复原状时,这些势能则转换为动能,符合能量守恒原理.在弹簧问题中,可以利用这一原理来分析弹簧系统在不同状态下的能量变化[3].

例1 如图示1所示,在甲场景中,有两个物块m1和m2被一个轻弹簧连接在一起,它们会在水平地面上呈现静止状态.在某一个时刻,m1获得一个水平向右的速度.从这一时刻起,开始观察两个物块的运动情况.图乙显示了随时间推移,两个物块的速度变化情况.以下判断正确的是( ).

图1 例1题图

A.t1时刻,弹簧最短

B.在t1～t3时间内,弹簧将呈现压缩状态

C.在0～t2时间内,弹簧对物块m1冲量的大小为m1(v0-v3)

D.物块m1、物块m2的动量满足m1v0=(m1+m2)v2=m2v1-m1v3

解析在这个场景中,m1在初始时刻获得了速度v0,导致弹簧开始被压缩.在这个过程中,m1开始减速,同时m2开始加速,直到t1时刻,它们的速度相等.在当前时刻,系统的动能达到最小值,弹性势能则达到最大值,同时弹簧被压缩至最短的状态.在t1时刻之后,m2持续加速,而m1则首先减速至零,然后反向加速.随着时间的推移,到达t2时刻,弹簧恢复到原始长度状态,这时两个物体的速度方向相反.因此,弹簧的长度逐渐增加,两个物体都经历减速运动,直到t3时刻,两者的速度再次相等.在这一时刻,系统的动能再次达到最小值,弹性势能最大,同时弹簧的伸长量也达到最大.因此,选项A是正确的;选项B是错误的;选项C是错误的,因为在0到t2时间段内,弹簧对m1的冲量是-m1(v3+v0);选项D是正确的,因为在0到t1和0到t2的时间段内,将弹簧和两个物体视为整体时,合外力为零,因此满足动量守恒.

3.2 能量守恒在传送带问题当中的应用

在传送带问题中,能量守恒原理是解决物体运动和能量转化问题的重要工具.为了帮助学生更好地理解能量守恒在传送带问题中的应用,教师可以采用一题多解的方式进行解答.这种方法在分析物体在传送带上的运动和能量转化时,能够通过不同的角度和方法得出相同的答案,从而深入理解能量守恒的应用[4].

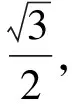
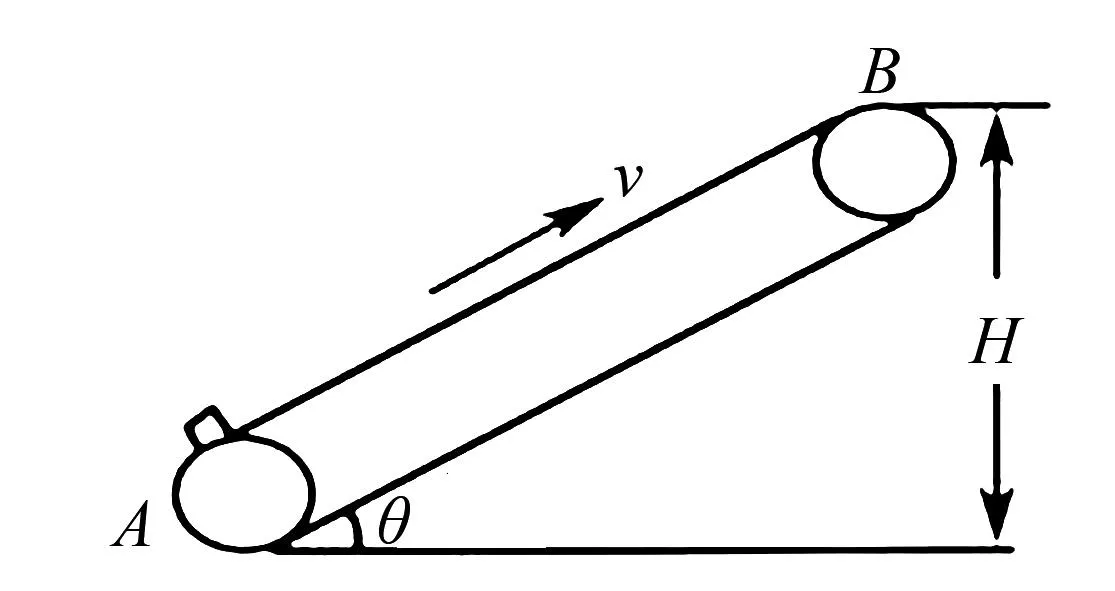
图2 例2题图

(1)从点A到点B,利用运动学公式来计算其所用时间?

(2)传送物体电动机多消耗多少能量?

解析(1)沿传送带方向工件受到来自传送带的向上摩擦力和重力的向下分力.利用牛顿第二定律分析可知,工件最初的加速度为2.5 m/s2.导致它在传送带上先匀加速运动0.8 m,然后以恒定速度运动3.2 m.

(2)方法一:从对传送带做功角度来看,物体置于传送带后,它对传送带施加了向下的摩擦力.为保持传送带以匀速运行,电动机需提供额外的力量.这种额外力量的施加是为了克服物体与传送带之间的摩擦,并维持传送带的恒定运动速度.在物体加速阶段,多出来的电动力:F1=f1=μmgcosθ=75 N.这个多出来的电动力对传送带做功为:W1=Fvt1=120 J.在物体匀速的阶段,摩擦力变为静摩擦,这个多出来的电动力为:F2=f2=mgsinθ=50 N.这个多出来的电动力对传送带做功:W2=Fvt2=160 J.所以多出来的电动力做功为:W=W1+W2=280 J.

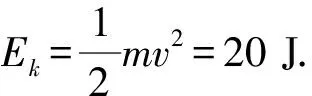
3.3 能量守恒在抛体问题当中的应用

抛体运动包括了动能与势能的不断转化,以及空气阻力对能量转化的影响.利用能量守恒原理,可以确定抛体运动中的关键时刻,例如抛出时、到达最高点时等.这些时刻对于理解能量转化的过程和解答问题至关重要.在教学中,教师应通过案例分析和问题引导,指导学生应用能量守恒原理解决抛体问题,有助于学生更深入地理解能量守恒在抛体运动中的应用,提高其解题能力和问题分析能力[5].

例3 如图3所示,当篮球在向下掉落的过程中,如果它最初以一定的角速度绕水平轴转动释放,它将在运动过程中受到阻力f1和偏转力f2的影响,而这两个力与篮球的速度v有关.其中,阻力f1与篮球速度的平方成正比(f1=k1v2),反方向于篮球的运动方向.而偏转力f2与篮球的速度成正比(f2=k2v),且方向与篮球运动方向垂直.下列说法正确的是( ).

图3 例3题图

A.篮球的阻力和偏转力的大小由常量k1和k2决定,与篮球的角速度无关

B.篮球回到起始高度时,其角速度有可能与初始释放时的角速度相等.

C.如果站得足够高,并在适当的释放条件下,篮球在着地之前可能呈现向上运动的趋势.

D.在适当的释放条件下,篮球可能在空中保持水平直线运动一段时间.

解析当篮球被释放时,开始转动,引入了偏转力f2=k2v的作用,这个力会垂直于篮球运动方向.这个偏转力的大小与篮球的转动速度相关,所以选项A错误.由于空气阻力对篮球做负功,篮球的机械能会逐渐减小.所以篮球将不会具有足够的能量在其运动过程中重新达到原来释放时的高度.因此B错误.篮球在下落过程中,受到空气阻力和偏转力的影响.尽管空气阻力持续减小篮球的速度,但是偏转力的方向可能使篮球竖直向上运动,这意味着篮球在落地前可能具有上升趋势,所以选项C是正确的.然而,篮球速度减小后,偏转力也会减小,使得无法持续在水平方向上运动,因此选项D错误.

4 结束语

综上所述,在高中物理学习中,能量守恒的运用是解决问题的关键.教师在教学过程中的引导和示范对学生理解和应用这一定律至关重要.通过深入基础知识的讲解和具体例题的演示,学生能更好地掌握物理问题的解题技巧.因此,重视能量守恒在教学中的应用,有助于学生更深入地理解物理现象背后的原理,并提升他们的解题效率和能力.