高中数学不等式易错题型和解题教学
姜 辣
(南京市建邺高级中学,江苏 南京 210000)
在高中数学中,不等式不仅仅是一个独立的知识点,还深深嵌入在代数、几何、函数,甚至是概率统计等多个数学分支之中.因此,正确应用不等式,是学生在整个高中数学学习过程中不可或缺的能力[1].然而,在实际教学中发现,许多学生会因为误解不等式性质、疏忽计算过程、选择不当的解题策略等原因,在处理不等式题目时陷入困境,甚至犯下错误.这些错误不仅直接影响了他们的答题正确率,还导致他们对整个不等式知识体系的理解出现偏差,进而影响到他们在其他相关数学知识点的学习和理解.因此,本文将重点针对这些常见的易错题型进行分析,通过探讨原因并提供相应的解题策略,帮助学生避免和纠正这些错误,从而更好地掌握和运用不等式知识,提高他们的数学解题能力.
1 易错题型分析
1.1 不等式组及其解题方法
不等式的解集和不等式组的解集是不同的,常见的易错点包括对于不等式的联立方程和求解方法不理解,对于解的范围和形式的产生误解.对于单个不等式,解集通常由半开区间或闭区间构成,要注意考虑限制条件和特殊情况,正确求解不等式[2].而对于不等式组,解集通常由各个不等式解集的交集或并集构成,要注意联立的方式和解的数量,正确求解不等式组.
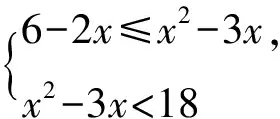
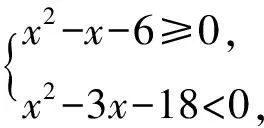
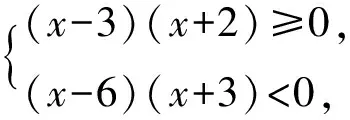
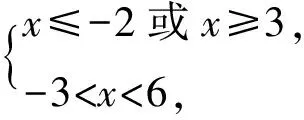
所以-3 所以不等式的解集为{x|-3 点评学生要加强对不等式的解法和解的表现形式的理解,多进行实战演练和推导计算,并注意题目中的一些特别提示和隐含条件,以便正确地求解不等式和不等式组,提高解题的准确度和效率. 在求解绝对值不等式时,我们需要根据符号的不同分类讨论,将不等式拆分成多个情况求解,并验证解是否符合原不等式.这类问题的易错点常常因学生不能正确理解绝对值符号含义而出现.学生在求解过程中,会忽略实际情况下的取值,导致在“去绝对值”符号求解时,出现细节性的错误. 例2 已知函数f(x)=|x-a|+|x+3|. (1)当a=1时,求不等式f(x)≥6的解集; (2)若f(x)>-a,求a的取值范围. 解(1)当a=1时,f(x)=|x-1|+|x+3|, 即求|x-1|+|x+3|≥6的解集, 当x≥1时,原不等式可化为2x+2≥6,得x≥2; 当-3 当x≤-3时,原不等式可化为-2x-2≥6,得x≤-4. 综上,不等式f(x)≥6的解集为 {x|x≤-4或x≥2}. (2)f(x)=|x-a|+|x+3|≥|(x-a)-(x+3)|=|a+3|, 当且仅当(x-a)(x+3)≤0时,等号成立. 所以f(x)min=|a+3|>-a, 当a<-3时,原不等式可化为-a-3>-a,无解; 当a≥-3时,原不等式可化为a+3>-a, 点评对于绝对值不等式,有三种求解方法:(1)利用分类讨论法“去绝对值”符号,将绝对值不等式问题变为普通的不等式问题;(2)当不等式两端均为正数时,可以对两边分别平方,将其转化为普通不等式求解;(3)根据绝对值的几何意义,结合数形结合思想进行求解.学生在解决绝对值不等式问题时,需要仔细理解符号含义、进行明确分析、加强细节注意. 一元二次不等式是不等式中的常见问题之一,常常涉及二元一次方程组、二次函数等概念,常见的易错点包括忽略不等式的限制条件.比如分母不能为零、公式运用错误、平方根法则,未充分了解不等式的形式和解的数量导致求解错误,等等. 即不等式qx2+px+1>0的解集为{x|-2 点评求解步骤: 第一步:审结论——明确解题方向 如要解qx2+px+1>0,最好能确定p,q的值. 第二步:审条件——挖掘题目信息 利用一元二次方程的根与一元二次不等式的解集的关系列出关于p,q的方程组. 第三步:建联系——找解题突破口 由给定不等式的解集形式→确定关于p,q的方程组→求得p,q→代入所求不等式→求解qx2+px+1>0的解集[3]. 线性规划问题是高考数学考试中的热门考点,通常以选择题、填空题的题型呈现.这类问题的难度一般不大,但需要学生熟练掌握线性不等式的基本概念和解题方法.学生在求解该类题型时,常见的错误有:对约束条件的理解不准确、忽略约束条件的实际情况、利用代交点法直接求解、认为目标函数的最大值对应的情况是截距最大等. 图1 例4题解析示意图 点评线性规划问题有三种常见题型:一是求解目标函数的最值问题;二是求解所形成的区域面积;三是求解目标函数的取值范围.解决该类问题,数形结合思想必不可少.为了避免解题过程出现错误,要严格按照“画”“移”“求”“答”四个步骤进行.“画”即画图确定可行域;“移”即根据目标函数的几何意义,结合图象,找到目标函数的最值对应的点;“求”即将对应的点坐标代入目标函数中;“答”即回答对应问题. 以下是一些解决高中数学中不等式易错题目的解题教学策略. 一是建立完整的知识体系.不等式成立与否的判定和解题方法,本质上要依赖于运算规律和不等式性质.因此,在学习不等式的时候,需要先建立完整的不等式知识体系.包括理解不等式的含义、不等式的基本性质、不等式的基本运算及其法则等方面,以及需要熟练应用这些知识进行解题. 二是掌握不等式的基本性质.不等式的基本性质包括加减同项、乘除同因、同向性等,是解决不等式问题的基础.学生需要熟练掌握这些不等式的基本性质,并且在解题过程中正确运用,从而避免因运算错误而导致的答案错误. 三是学会使用变形和替换技巧.在解决不等式问题中,变形和替换是非常重要的技巧.学生需要掌握常见的变形和替换技巧,例如平方两边、提取公因数、配方等.在运用这些技巧的时候,学生需要注意是否改变了不等式的大小关系,避免由于运算错误而导致的答案错误. 四是掌握一些常见的不等式套路题目.不等式套路题目包括均值不等式、柯西不等式等.学生需要熟悉这些不等式套路题目的应用场景,并且学会根据题目的要求选择合适的不等式套路,从而解决问题. 五是要注重数学归纳法的运用.数学归纳法在解决不等式问题时是非常有效的方法.通过数学归纳法证明不等式的正确性可以增加学生解决不等式问题的信心,同时也有助于提高学生的系统性思考和证明能力[4]. 通过上面的讨论,可以发现不等式问题的常见错误类型,以及避免这些问题的相应教学策略,希望给一线教师提供参考.1.2 绝对值不等式及解题方法
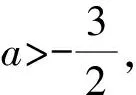
1.3 一元二次不等式及解题方法
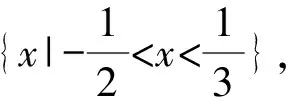
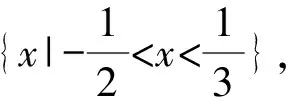
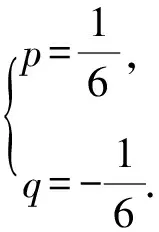
1.4 线性规划及其解题方法
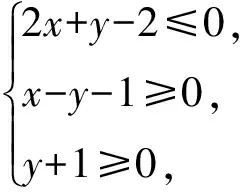
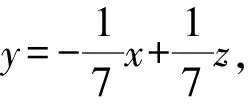
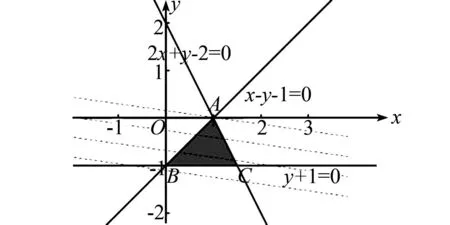
2 解题教学策略
3 结束语

