向量在高中数学解题中的应用研究

胡 涛

(常熟市尚湖高级中学,江苏 常熟 215500)

向量作为数学中的重要概念之一,在几何、代数等领域都扮演着重要角色.它不仅为解决各类数学问题提供了一种全新的思维方式,也为理解和应用数学提供了更广阔的视野.

1 向量的概述

向量是数学中的一个重要概念,用于表示有大小和方向的物理量或几何对象.向量可以在不同的领域中应用,例如物理学、几何学、计算机图形学等.

向量可以进行多种运算,包括加法、减法、数量积和向量积等.在进行向量的加法和减法时,将两个向量的起点连接起来形成一个平行四边形,然后从平行四边形的对角线上取出向量的终点作为结果向量的终点[1].向量的数量积(也称为点积或内积)是一个标量,等于两个向量的模的乘积与它们之间的夹角的余弦值的乘积.在几何学中,向量的运用较多,可以表示平面上的点、线段、直线、平行线、垂直线等几何对象,并且能够进行多种几何变换.向量还可以用来解决方程组、证明等式和不等式、计算三角函数值、描述取值范围以及处理数列等问题.

2 高中数学解题中应用向量的必要性

(1)简化计算.向量的运算规则可以帮助我们简化计算过程.通过使用向量的加法、减法、数量积等运算,可以将复杂的数学问题转化为更简单的向量运算问题.这使我们能够更快、更准确地解决问题,减少繁琐的计算步骤.

(2)提供几何直观.向量可以用来表示几何对象,如点、线段、直线等.通过向量的几何表示,我们可以更直观地理解问题的几何性质.通过将问题转化为向量的几何问题,我们可以更好地利用几何直观解决问题,而不仅仅依赖于抽象的代数符号.

(3)解决复杂方程组.向量可以用来解决一些复杂的方程组.通过将方程组转化为向量形式,我们可以利用向量的线性组合和矩阵的运算来求解方程组.这种方法可以简化方程组的求解过程,特别是当方程组包含大量变量和方程时[2].

(4)统一概念和方法.向量是一种统一的数学概念,可以应用于不同的数学领域.通过使用向量,我们可以将不同的数学概念和方法联系起来,形成一个整体的数学体系.

(5)推广应用.向量不仅在高中数学中有应用,还在许多其他学科和实际问题中有广泛的应用.通过学习和应用向量的概念和方法,我们可以为将来的学习和职业发展打下坚实的基础.向量的应用范围包括物理学、工程学、计算机科学等领域..

3 高中数学解题中向量的应用

3.1 向量在平面几何中的应用

向量可以用来表示平面上的点、线段、直线、平行线、垂直线等几何对象.通过向量的加法、减法和数量积等运算,可以进行向量的平移、旋转、镜像等几何变换.此外,向量的模可以用来计算线段的长度、直线的斜率等.

例1 如图1所示,正方形ABCD,点P在BD上,且PECF为矩形,证明:PA=EF.

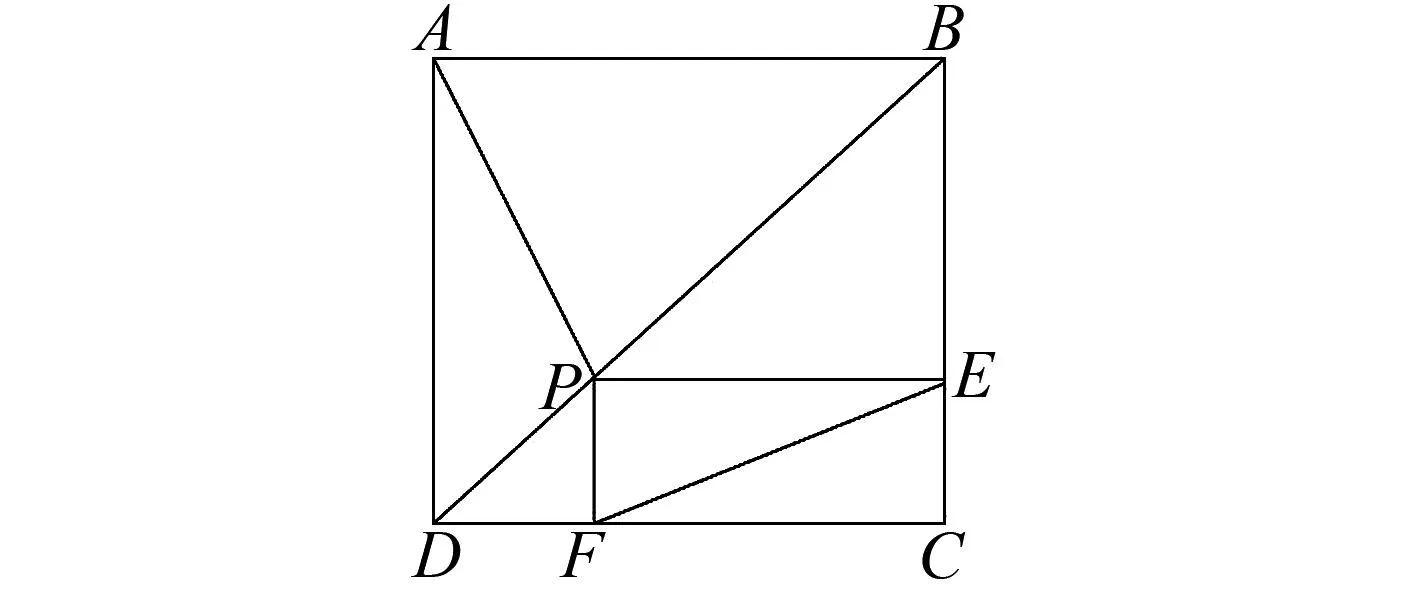
图1 例1题图

证明:建立坐标系,如图2所示.

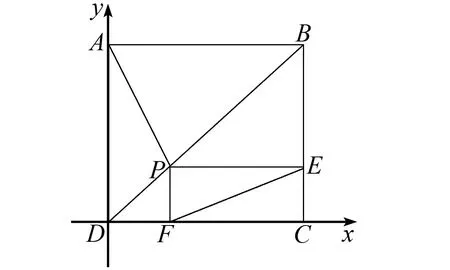
图2 证明示意图

DF=PF=λ,点F坐标为(λ,0),点E坐标为(1,λ),点P的坐标为(λ,λ).

3.2 向量在等式(不等式)证明中的应用

向量的性质可以用来证明等式和不等式.通过向量的加法、减法、数量积等运算,可以推导出一些等式和不等式的性质,从而进行证明.

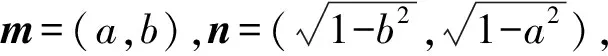
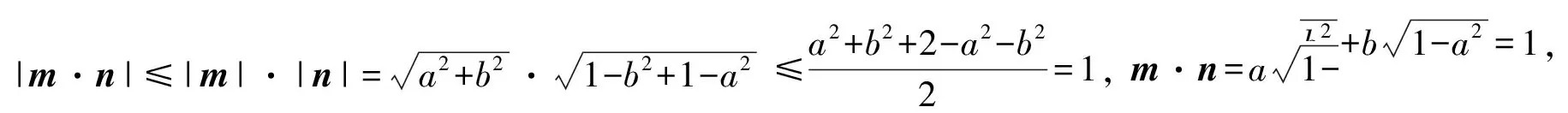
∴1≤|m·n|≤1,因此|m·n|=1,m向量和n向量共线平行,a2+b2=1-b2+1-a2,求得a2+b2=1.

3.3 向量在取值范围中的应用

向量的模、数量积、坐标和方向角等可以用来描述向量的取值范围.通过理解向量的取值范围,可以解决一些与向量相关的问题,如向量的大小比较、向量的正交性等.

例3 单位向量a·b=0,且|c-a-b|=1,求|c|的取值范围.

解因为a﹒b=0,所以a与b为互相垂直的单位向量,因为|c-a-b|=1,所以|c-(a+b)|=1,绘图如3所示,得到a+b,绘制c后,得到c-(a+b).

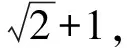
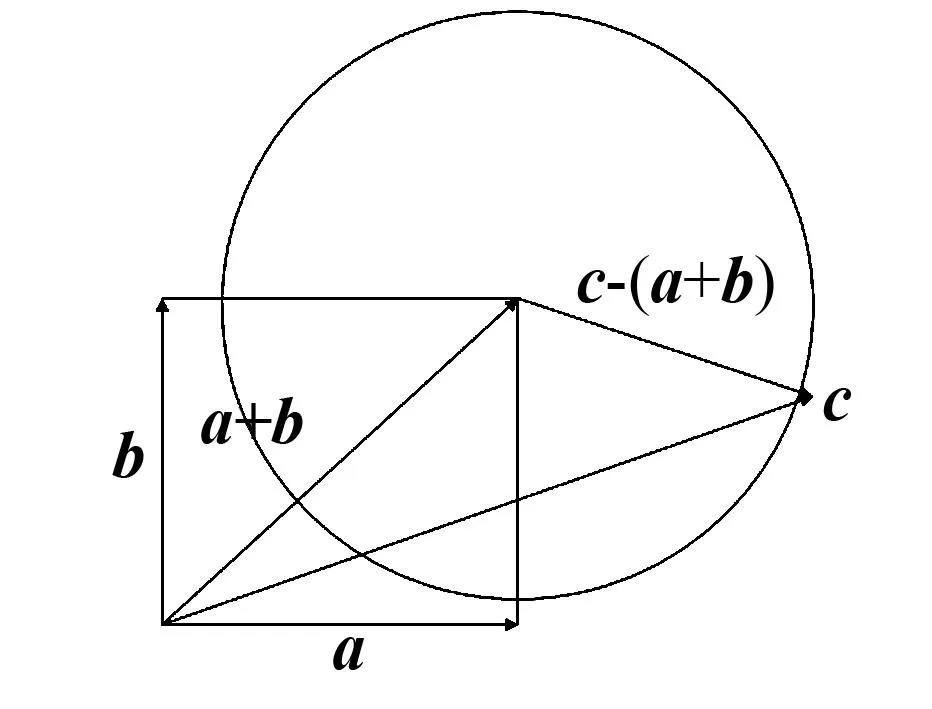
图3 例3解析示意图

3.4 向量在数列问题中的应用

向量可以用来表示数列的通项.通过向量的运算和性质,可以推导出数列的递推关系或通项公式,从而解决数列问题.向量的求和、差分、乘法等运算可以用来计算数列的和、差分列等.

例4 已知△ABC中三边长a、b、c为等差数列.

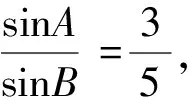
解(1)因为sinA∶sinB=3∶5,

所以a∶b=3∶5,

令a=3k,则b=5k(k>0),

因为三边长a、b、c依次成等差数列,

所以c=7k,

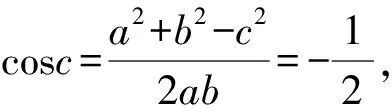
(2)因为b=1,三边长a、b、c依次成等差数列,

所以a+c=2;

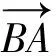
所以accosB=b2-(a-c)2,

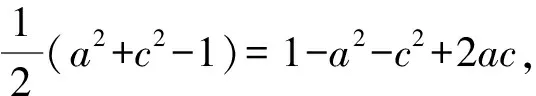
所以3(a+c)2-10ac=3,将a+c=2代入,

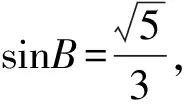
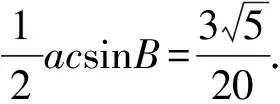
4 高中数学解题中应用向量的注意事项

在高中数学解题中应用向量时,有几个注意事项需要考虑:

(1)理论与实践结合.向量的教学应该结合理论和实际应用,让学生明白向量的概念、性质和运算规则,并能够应用到实际问题中.通过具体的例子和实际应用的问题,帮助学生理解向量的意义和用途.

(2)强调几何直观.向量在几何中的意义和应用是理解向量的重要基础.在向量的教学中,应该强调几何直观,让学生能够通过向量的几何表示来理解问题和解题思路.通过绘制向量图形、探索几何性质等方式,使学生的几何直观能力得到提升[3].

(3)注重问题解决过程.向量的教学应该注重问题解决过程的训练.通过引导学生分析问题、建立数学模型、选择合适的向量运算和推导方法,培养学生的问题解决能力和数学思维能力.

(4)强化基本概念和运算.向量的教学应该注重基本概念和运算的理解和掌握.学生需要清楚向量的定义、向量的模、方向、坐标等基本概念,并能够熟练运用向量的加法、减法、数量积等运算规则.通过大量的练习和应用题,巩固基本概念和运算的掌握[4].

(5)强调数学语言和符号.向量的教学中应该强调数学语言和符号的使用.学生需要学会用准确的数学语言描述向量的性质和运算规则,并能够正确使用向量的符号表示和计算.

(6)多样化教学方法.向量的教学应该采用多样化的教学方法,包括讲解、示范、练习、探究、实践等.教师可以根据学生的学习特点和需求,选择适合的方法和教学资源,激发学生的学习兴趣和积极性.

5 结束语

向量在高中数学解题中起到了重要的作用,它不仅丰富了解题的方法和思维,还培养了学生的空间想象力和抽象思维能力.合理地应用向量,学生可以更好地理解和应用数学概念,进而提高解题的准确性和效率.