基于高考“数列”专题 探究解题技巧

江晓洁

(福建省诏安第一中学,福建 漳州 363500)

纵观近五年数学高考题目,数列部分着重对数列的通项、求和等知识点进行考查.常与函数、不等式等知识整合到一起,对学生的数学综合素养进行考查.

1 数列概念类题目解题分析

纵观最近五年数列考查题目,存在大量的基础性问题.通常,这一类型问题难度系数比较低,主要围绕等差、等比数列的概念展开考查,学生只要掌握深刻理解概念即可完成解答.

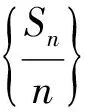
A.甲是乙的充分条件但不是必要条件;

B.甲是乙的必要条件但不是充分条件;

C.甲是乙的充要条件;

D.甲既不是乙的充分条件,也不是乙的必要条件

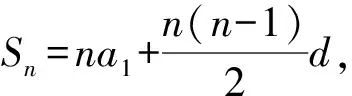
综上得知,{an}是等差数列,即选项C是正确答案.

2 数列通项公式解题分析

在高考题目中,求数列通项公式这一类型的题目比较常见,其难度系数属于中等水平,并常常出现在选择题、填空题、解答题目中的第一个小问题.在这一类型的题目中,常见的形式主要包括:由递推公式、已知前n项和、已知前n项及第n项关系式求通项公式.通常,在解答这一问题时,可结合不同的题目类型,选择不同的解题方法[1].

例2记Sn为数列{an}的前n项和,已知a2=1,2Sn=nan,求{an}通项公式.

解析该题目是2023年全国甲卷理科17题中的第一问,本题目中主要对数列的通项公式进行考查,题目难度系数比较低.通常,针对已知明确数列类型的题目,可直接运用等差数列或者等比数列的定义进行求解.

已知2Sn=nan,当n=1时,2a1=a1,即a1=0,

当n=3时,2(1+a3)=3a3,即a3=1,

当n≥2时,2Sn-1=(n-1)an-1,

即2(Sn-Sn-1)=nan-(n-1)an-1=2an,

对其进行化简得出(n-2)an=(n-1)an-1,

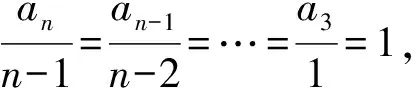
即an=n-1.

综上分析得出an=n-1(n∈N*).

例3已知{an}满足a1=3,an+1=3an-4n,计算a2、a3,猜想{an}通项公式并证明.

解析该题目是2020年高考全国Ⅲ卷理科17题,在本题目中给出了数列{an}的首项,以及前一项和后一项的关系式.本题目意思相对比较清晰明了,根据题目中的已知条件和所求的问题,解题的关键在于利用首项和关系式这两个条件.通常,在解决这一类型数列问题的时候,学生可从构造法、归纳法两个角度进行探索.

解根据an+1=3an-4n以及a1=3这两个条件,可直接求出a2=5,a3=7,由此猜想出an=2n+1,n∈N*.

证明:根据题目已知条件得出an+1-(2n+3)=3[an-(2n+1)],则有bn=an-(2n+1),因此bn+1=3bn,且b1=b2=0,即bn=0.因此,猜想an=2n+1,n∈N*成立.

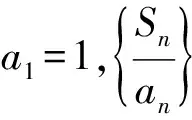
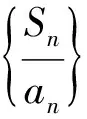
3 数列求和类题目解题分析

在高中数学数列考查题目中,数列求和尤为重要,常见于一些综合性题目.通常,在解决这一类型问题时,学生不仅仅要熟练掌握等差数列、等比数列的求和公式,还应掌握一定的解题技巧,包括错位相减法裂项求和法、分组求和法、倒序相加法等.

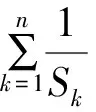
解析本题目是2020年某地高考模拟试题中的一道填空题.就本题目而言,难度系数相对比较低,学生只要认真观察题目的特点和已知条件,即可采用裂项法进行求和,将数列{an}的每一项进行分解,最终通过依次项抵消、间隔项抵消等方式进行解答.

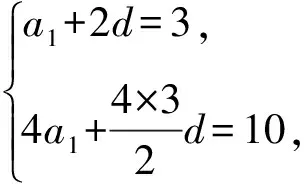
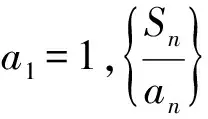
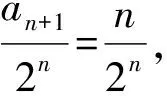
4 基于数列高考题目特点的教学启示

根据高考数列题目分析发现,近几年关于数列题目的考查,方式相对比较稳定,并且考查内容全面,突出了数学思想、关键能力的考查.同时,在新课标视域下,考查的形式也随之更加新颖,将其蕴含到实际生活情境中.例如,2022年全国新高考Ⅱ卷中的题目中,以中国古代建筑作为背景;在2023年北京卷中,渗透了一定的数学文化;另外,在数学高考题目中,数列题目还常常与函数、不等式、概率等问题结合到一起.面对这一全新的考查特点,教师在日常教学中,必须关注以下几个方面.

首先,重视基础教学.教材是新课标的具体体现,也是教师开展课堂教学的重要依据.正所谓“万变不离其宗”,教材上的基础知识是学生解答数列问题的根基.因此,教师在组织课堂教学时,必须认真研读教材内容,并基于教学目标和学生的实际情况,科学运用多种方法开展基础教学,使学生深入理解概念、性质、公式等;同时,教师还应关注基础题目教学,力求通过变式训练等方式,使学生在少而精的题目训练中,逐渐提升自身的逻辑思维能力.

其次,关注数列性质,加强知识联系.纵观当前高考中的数列题目,多数都是以数列的性质作为依据,学生需要根据数列的性质分析题目、解决问题.

再次,强化数列的综合应用.根据新课标下的数列考查方向和趋势,教师在日常教学中,还必须坚持理论联系实际的原则,将数列知识和实际生产和生活联系起来,使学生在实际问题中,抽象出数列模型,并运用数列的相关知识进行解答.

最后,积累解题经验,提炼数学思想.鉴于新高考下的数列题目考查特点,教师在开展课堂教学时,必须摒除“机械化刷题”的教学模式,引领学生对所做的题目、错题进行反思和分析.使学生在总结、分析、归纳的过程中,掌握一定的解题规律和方法,并从解题中将数学思想提炼出来,让学生在日常学习中逐渐提升自身的解题素养[4].

5 结束语

教师应熟悉新高考的考查要求,结合数列高考试题进行教学实践,及时调整和优化课堂教学方案,不断提升数列解题教学效果.