基于混合“集装箱-快递”物流需求的跨境电子商务配送路线优化研究

文/陈克莹

1.跨境电子商务配送路线优化

1.1 建立混合“集装箱-快递”物流需求回归模型

构建混合“集装箱-快递”物流需求的多元回归模型，对跨境电子商务物流需求量的影响因素进行分析。经过对于数据的提取与分析，获得因变量与自变量之间的关系，并推测出影响变量的数据。在模型构建过程中，通过分析两个变量之间的关系，计算物流需求量，合理安排物流线路和运营[1]。同时，根据对于混合“集装箱-快递”物流需求，对其影响因素进行分析后得到跨境电子商务物流规模数据。设定自变量经济指标为X，随机变量为Y，回归模型表示为：

公式中：δ 为回归参数；δ 为随机误差。通过模型计算得到对应的样本数据，并形成对应矩阵。将需求分析运用SPD软件对数据进行提取，将初始数据进行归一化处理后，对变量之间的参数关系进行分析。对模型进行拟合度检验，设定修正系数为R。经过计算估计样本的回归方程，并得到拟合样本的观测值。设定样本数据为原始序列，将原始序列进行累积，得到新的序列。并对累积的序列进行平滑处理。运用最小二乘法对参数矩阵的值进行计算，得到参数值为x，y，将两个值代入序列中进行还原，得到预测函数[2]。根据预测函数计算模型的相对残差值。比较残差值与模型的精度误差，判断预测模型是否符合预测精度。将得到GM（1,1）预测模型中的w设定为组合权重系数。计算权重后进行比较，获得模型的平均绝对误差，以此来判断混合“集装箱-快递”物流需求模型预测效果。

1.2 节约里程法计算最短距离优化配送路线

设定物流配送车辆在起始点进行配货，在完成后按照路线返回配送中心O。在路线中存在N个配送站点并规划出n条起始线路[3]。选择所有行驶路径，并根据不同行驶路径长度，按照顺序将运输问题中的回路设定为（0，…，i，0）和（0，…，j，0）。将两个回路进行合并生成一个新的回路为（0，…，i，j，…，0），组合后得到新的车辆运输路径，并记录相应的距离变化。如果组合后的车辆总行驶距离较短，将与原有路径之间的差值作为节约距离。计算获得节约距离值，并将其进行排序。在符合车辆容量约束的条件下，按照计算得到的数值进行排序后依次安排对应的配送连接点[4]。将所有的配送站点进行连接后，由配送中心P0分别向站点Pi和站点Pj两点进行物流配送。选择路径A中的往返配送路线为P0-Pi-P0和P0-Pj-P0，配送距离长度表示为2（L1+L2）。选择路径B中的往返配送路线为P0-Pi-Pj-P0，配送距离长度为（L1+L2+L3），路线组合后车辆节约的行驶里程表示为：

公式中：L为线路里程。根据节约里程法得到配送路线的出发点，并选择对应的配送运输车辆的特征，按照不同站点到配送中心的距离进行最优线路配送规划。设定配送中心的物流工作为t，运用节约里程法对配送路径进行寻优，寻找线路中的最优路径[5]。在路线数据中随意生成了1×10条路径，并重复N次。将第i次生成的粒子放入一个规模为N×L种群的第i行中，使得其能够包含N个粒子规模的初始种群。运用对粒子群从第1列开始进行累加的计算方法，计算对应配送站点的货物信息，并将得到的信息进行累加。根据粒子群的搜索能力进行最优解搜索。不断进行迭代，后期粒子群收敛速度减弱，会发生陷入局部收敛而无法产生最优解。所以设定粒子迭代次数为N，得到的权重wmax。随机生成不同解，获得原始种群。计算粒子的适应度函数值，并对当前粒子群进行排序，获得极值。增加混沌数，对粒子群进行更新。确定迭代次数是否达到最大值，并输出最优解。将目标函数的倒数定义为适应度函数，设定配送中的变量，并对交叉点中的补集进行随机排列，根据更新后的位置进行交换，从而获得交换后的最佳点位置，得到最优路径。如果在某个站点中的货物信息累加结果超过了车辆载物的最大重量，或者超出了最大容积，则在该点之后添加0。如果没有超过车辆配送承载量，则需计算出从配送中心到此配送站点的距离，再加上从该站点返回配送中心的距离[7]。与车辆总行驶距离阈值进行比较，如果超出阈值范围，则需要在位置后面添加0，并将货物的信息重置为0。不断重复上述步骤，直到完成所有站点的配置。

2.实验测试与分析

为测试配送线路方法的优化程度，对不同算法的最优路径配送任务中，需要的车辆所行驶距离进行统计。设置四个小组，运用PSO算法、APSO算法、KMND算法的小组为对照组，运用本文方法的小组为实验组进行最优路径求解，将其与三种传统算法进行对比测试。

2.1 搭建实验环境

运用Matlab进行编程求解。搭建实验所用的硬件环境，主机的运行内存8G，主频325.4GHz，Intel i7 CPU为622GB。测试数据源自Solom on数据库，其中有200个车辆路径规划的实际数据。配送问题的路径优化数据规模为20～30之间，结合实际情况对目标进行约束后，确定运用数据规模20作为实验测试规模。对数据集中的数据进行处理，使得数据样例满足一定的离散性，能够使用不同配送站点需求的特征。设置实验所用的物流配送车辆为标准的配送车辆，净载货量在150～200kg，结合实际需求满足车辆装载上限为180kg。设置粒子群的迭代次数为1100代，计算得到的SSE值为2，初始惯性权重因子5.00，两个学习因子边界设置为3和0。

2.2 结果与分析

运用PSO 算法对照1组求解后得到的最优路径为：0-11-17-15-3-5-9-12-18-20-2-4-1-19-16-14-10-6-7-8-13-0。最优解显示需要3辆车来完成配送任务，每辆车行驶的路径上的网点编号为：

运用APSO 算法对照2组求解后的最优路径为：0-12-15-4-9-11-17-20-5-13-16-8-1-7-14-6-19-3-7-19-3-10-2-18-1-16-0。最优解显示需要3辆车来完成配送任务，每辆车行驶的路径上的网点编号为：

运用KMND算法对照3组求解后的得到的最优路径为：0-9-19-15-10-1-18-7-5-4-17-14-16-12-8-20-3-6-13-11-2-0。最优解显示需要3车来完成配送任务，每辆车行驶的路径上的网点编号为：

运用本文算法实验组求解后得到的最优路径为：0-3-18-10-11-1-9-7-6-20-8-15-17-16-14-5-13-19-2-4-12-0。最优解显示需要2辆车来完成配送任务，每辆车行驶的路径上的网点编号为：

根据需要完成配送任务的车辆数，进行仿真实验后测得车辆的总行驶距离结果，如下表所示：

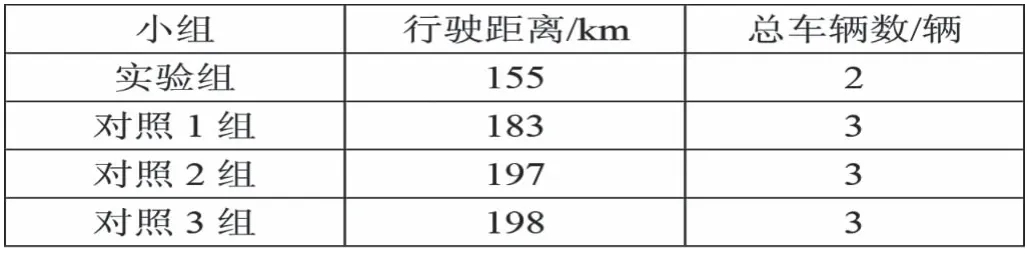
表1 车辆行驶距离

由实验结果可知，不同算法最优路径规划后，算法收敛速度缓慢使得对照组总车辆数较多，车辆行驶距离较长。而相比对照组，实验组算法在规划最优路径后，算法收敛速度明显增加，总车辆数减少1辆，行驶距离为155km，为四组中的最短距离。说明运用本文方法能够有效缩短车辆运行距离，获得较好优化结果。

综上所述，与传统路径规划方法相比，本算法在求解过程中受到的值界影响较小，所占的内存空间小，获得更高求解速度。通过对于算法的优化，减少了对求解结果依赖性，更好处理了搜索速度慢的问题，缓解了早熟的产生。在选择初始数据过程中，减少了计算开销，加大对于全局收敛性的计算，缩短车辆行驶距离，获得较好结果，验证了本文方法的有效应用。通过对混合“集装箱-快递”物流需求的跨境电子商务配送路线优化问题进行研究，建立优化模型，充分完善在快递配送问题中的车辆行驶距离问题，提升了配送效率，增加了车辆装载率。在处理大量需求的VRP问题的同时，可以对问题进行数据转化降维处理，不能够加快对于算法的计算速度，还能有效降低算法求解过程中陷入局部最优解的问题发生。运用多种算法对配送路径进行最优路径结果比对，获得最佳结果，体现了本文方法的实用性和有效性。在跨境电子商务配送过程中，能够有效减短车辆的行驶距离，提升了用户的满意程度，扩大了电子商务的运营范围，得到较好应用。

3.结束语

此次从跨境电子商务配送线路入手，研究了基于混合“集装箱-快递”物流需求的跨境电子商务配送路线优化方法。根据跨境电子商务配送路线的整体策略，选择混合物流需求，通过不断改进算法实现配送路线优化，为今后的研究提供了方向。但方法中还存在一些不足之处，例如部分算法尚未明确和简化，车辆的调配问题，采集数据单一等。今后应更加重视算法，提升配送中心服务水平和成本，满足用户配送需求，提升配送服务质量。丰富企业选址和路径优化。结合实际问题进行分析，实现基于混合“集装箱-快递”物流需求的跨境电子商务配送路线的全方位优化。