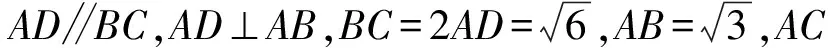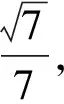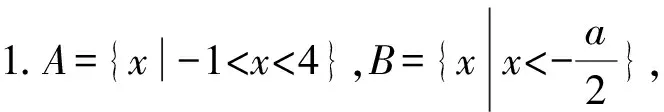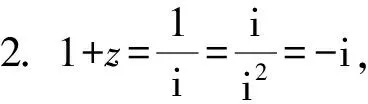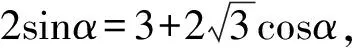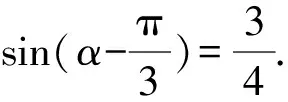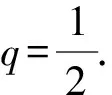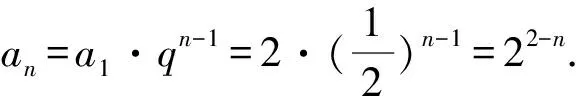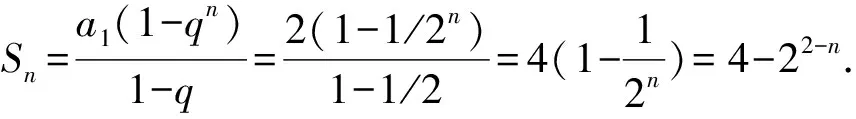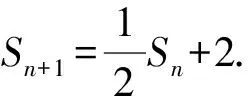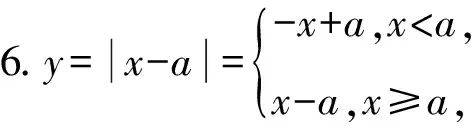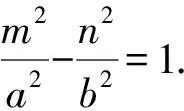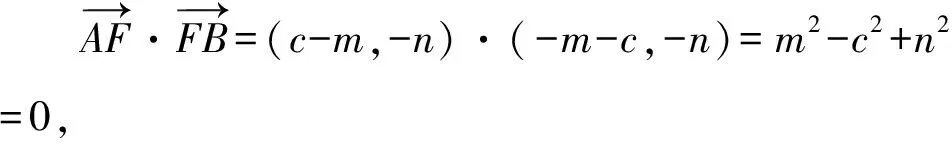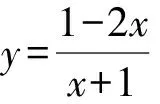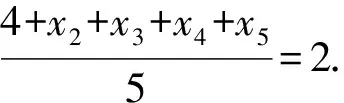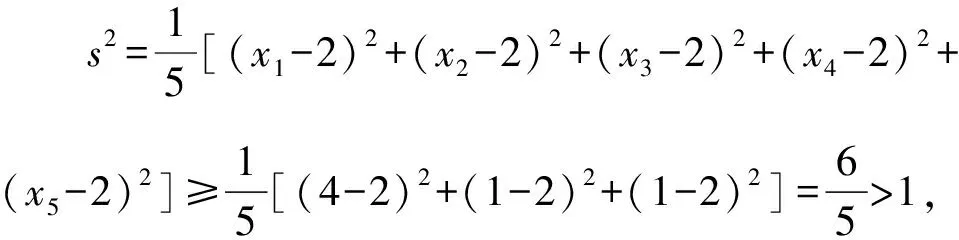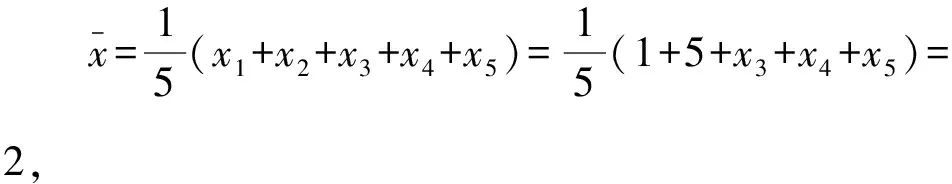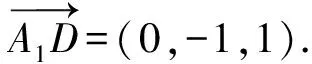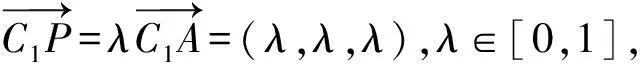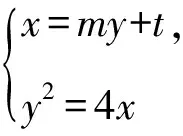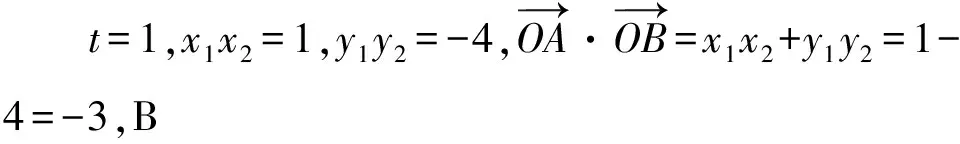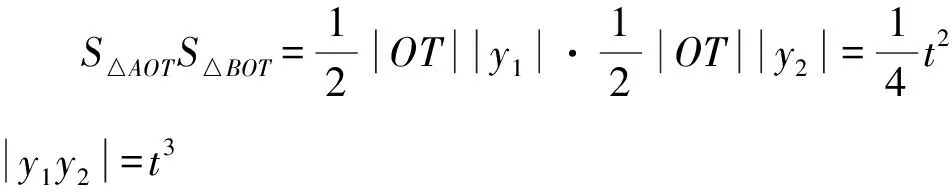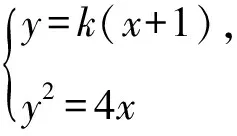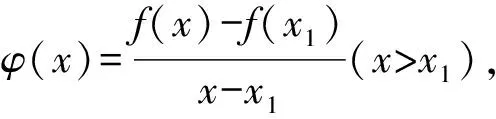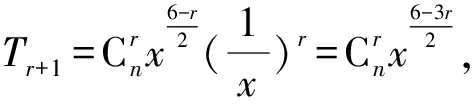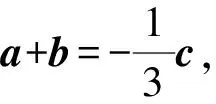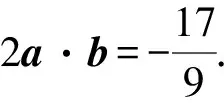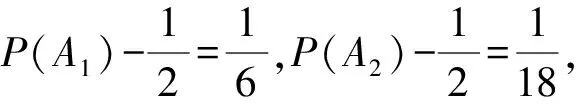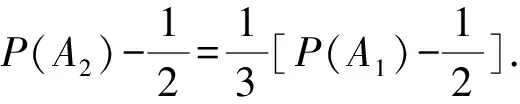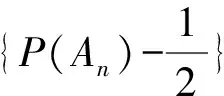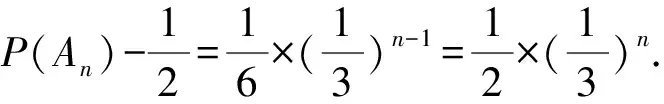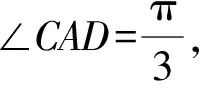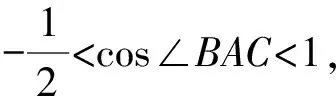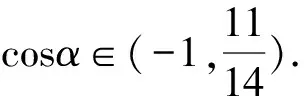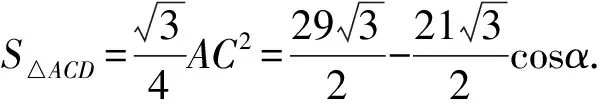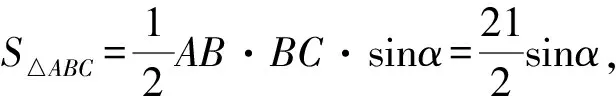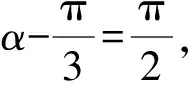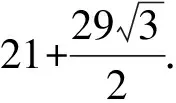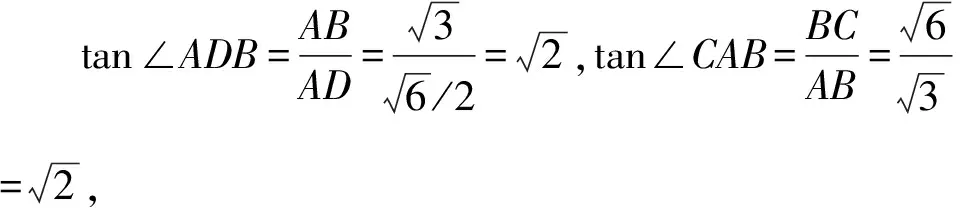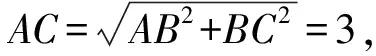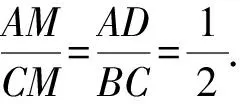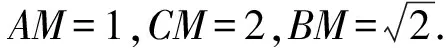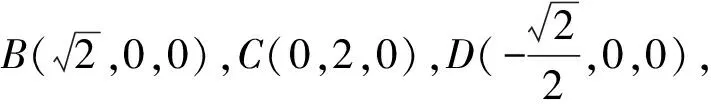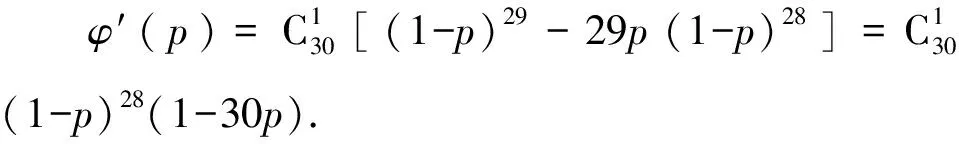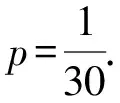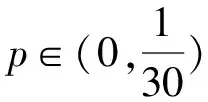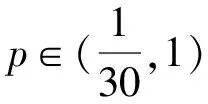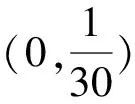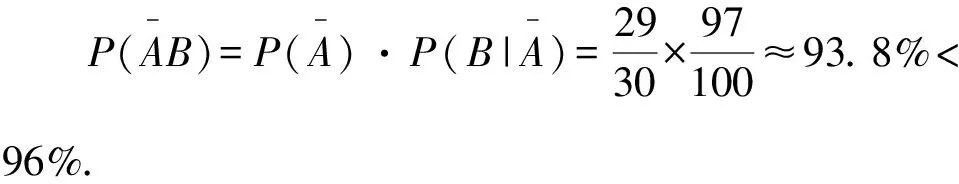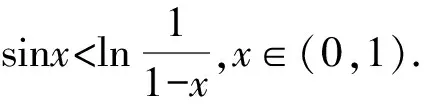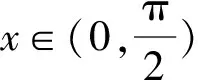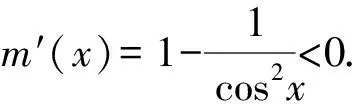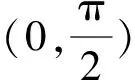2024年高考数学模拟试题(新高考)
林国红
(广东省佛山市乐从中学,广东 佛山 528315)
说明:(1)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
(2)本试卷适用省份:(新高考Ⅰ卷)山东、福建、湖北、江苏、广东、湖南、河北等省;(新高考Ⅱ卷)海南、辽宁、重庆等省市.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
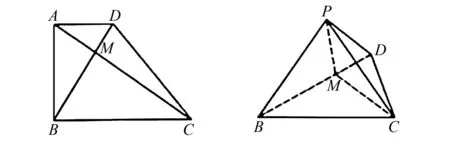
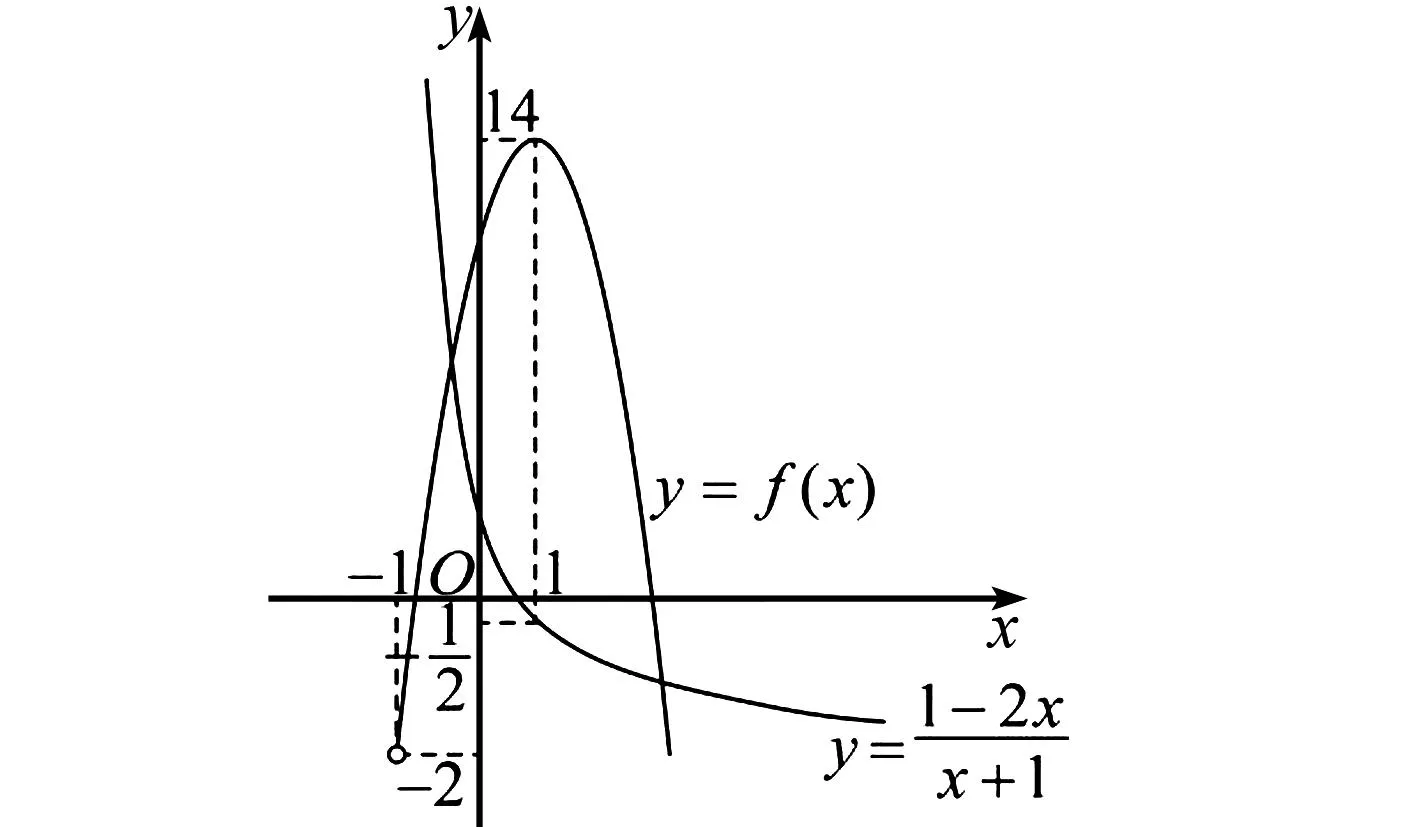
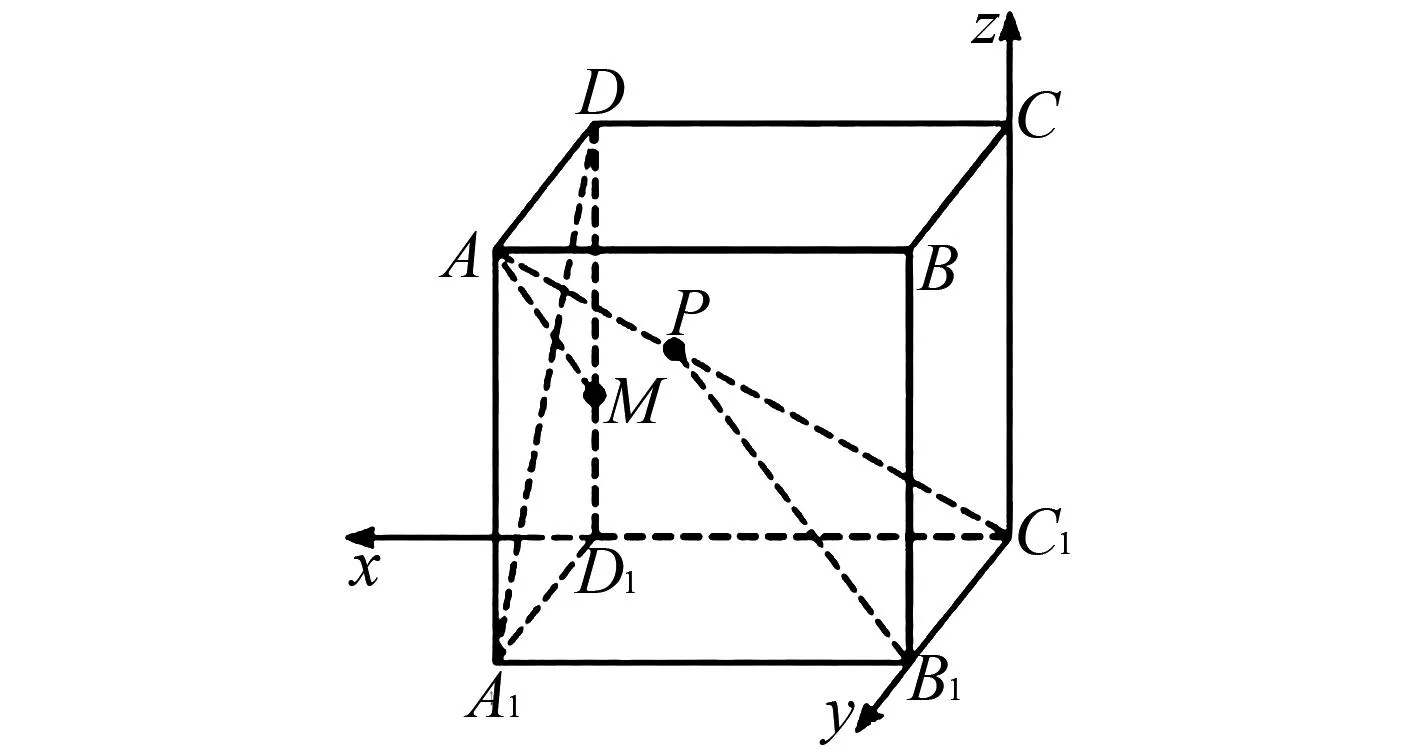
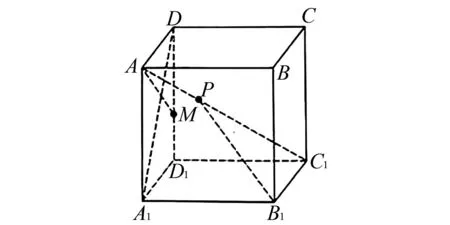
1.设集合A={x|(x+1)(x-4)<0},B={x|2x+a<0},且A∩B={x|-1 A.6 B.4 C.-4 D.-6 A.-2 B.0 C.2i D.-2i 4.已知等比数列{an}的首项a1=2,前n项和为Sn,且a1,2a2,4a3成等差数列,则( ). 5.某款对战游戏,总有一定比例的玩家作弊,该游戏每10个人组成一组对局,若一组对局中有作弊玩家,则认为这组对局不公平.现有50名玩家,其中有2名玩家为作弊玩家,一次性将50名玩家平均分为5组,则5组对局中,恰有一组对局为不公平对局的概率为( ). 6.a>2是函数y=|x-a|在(-∞,2]单调递减的( ). A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要 A.-16 B.-12 C.-9 D.-6 9.袋子中有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取5次,每次取一个球.记录每次取到的数字,统计后发现这5个数字的平均数为2,方差小于1,则( ). A.可能取到数字4 B.中位数可能是2 C.极差可能是4 D.众数可能是2 10.如图1,正方体ABCD-A1B1C1D1中,P是体对角线AC1上的动点,M是棱DD1上的动点,则下列说法正确的是( ). 图1 第10题图 C.对于任意的P,存在点M使得AM⊥B1P D.对于任意的M,存在点P使得AM⊥B1P 11.已知抛物线C:y2=4x的准线与x轴交于点D,O为坐标原点,点A,B是抛物线C上异于点O的两个动点,线段AB与x轴交于点T,则( ). A.若T为抛物线C的焦点,则线段AB的长度的最小值为4 C.若△AOT与△BOT的面积之积为定值,则T为抛物线C的焦点 D.若直线DA和直线DB都与抛物线C相切,则T为抛物线C的焦点 12.已知函数f(x)=exln(x+1),则( ). A.曲线y=f(x)在(0,f(0))处的切线方程为y=2x B.f′(x)在(0,+∞)上单调递增 C.对任意的x1,x2∈(0,+∞),有f(x1+x2)>f(x1)+f(x2) 15.已知圆C1:x2+y2=m2(m>0)与圆C2:x2+y2-2x-4y-20=0恰有两条公切线,则实数m的取值范围为____. 16.有n个编号分别为1,2,…,n的盒子,第1个盒子中有2个白球1个黑球,其余盒子中均为1个白球1个黑球,现从第1个盒子中任取一球放入第2个盒子,再从第2个盒子中任取一球放入第3个盒子,以此类推,则从第2个盒子中取到白球的概率是____,从第n个盒子中取到白球的概率是____. 17.已知等比数列{an}的各项均为正数,前n项和为Sn,若an+1+an+2=12an(n∈N*),S5=121. (1)求数列{an}的通项公式; (2)若bn=an+lnan,求数列{bn}的前n项和Tn. 18.如图2,在平面内,四边形ABCD的对角线交点位于四边形内部,AB=3,BC=7,△ACD为正三角形,设∠ABC=α. 图2 第18题图 (1)求AC的取值范围; (2)当α变化时,求四边形ABCD面积的最大值. 图3 第19题图 (1)证明:BD⊥PC; (1)求椭圆C的标准方程; (1)求每个芯片智能检测不达标的概率; (2)人工抽检30个芯片,记恰有1个不达标的概率为φ(p),求φ(p)的极大值点p0; (3)若芯片的合格率不超过96%,则需对生产工序进行改良.以(2)中确定的p0作为p的值,判断该企业是否需对生产工序进行改良. 22.已知a∈R,函数f(x)=(x-1)ln(1-x)-x-acosx,f′(x)为f(x)的导函数. (1)当a=0时,求函数f(x)的单调区间; (2)讨论f′(x)在区间(0,1)上的零点个数; 参考答案 4.设等比数列{an}的公比为q, 由于a1,2a2,4a3成等差数列, 所以4a2=a1+4a3,4a1q=a1+4a1q2. 由于a1=2,所以4q2-4q+1=(2q-1)2=0. 则Sn+1=4-21-n. 5.所有对局中,恰有一组对局是不公平对局的情况为:2名外挂玩家都分到了同一组对局,记该事件为事件A,则 故选C. ① ② 即C(4c+3m,3n). ③ 代入③并整理,得 2c2+3mc+a2=0. 由①②及a2+b2=c2,得 所以(2c2+a2)2=9m2c2=18a2c2-9a4. 即2c2-7a2c2+5a4=(2c2-5a2)(c2-a2)=0. 8.令f(x)=-x3-3x2+9x+9,则f(x-1)=-(x-1)3-3(x-1)2+9(x-1)+9=-x3+12x-2, f(-x-1)=-(-x-1)3-3(-x-1)2+9(-x-1)+9=x3-12x-2. 所以f(x-1)+f(-x-1)=-4 所以f(x)关于(-1,-2)中心对称. 因为f′(x)=-3x2-6x+9=-3(x+3)(x-1),所以当x∈(-∞,-3)∪(1,+∞)时,f′(x)<0;当x∈(-3,1)时,f′(x)>0. 所以f(x)在(-∞,-3),(1,+∞)上单调递减,在(-3,1)上单调递增. 所以f(x)的极小值为f(-3)=27-27-27+9=-18,极大值为f(1)=-1-3+9+9=14. 图4 第8题解析图 故选B. 9.设这5个数字为x1,x2,x3,x4,x5, 可得x2+x3+x4+x5=6. 对于BD:例如2,2,2,2,2,可知这5个数字的平均数为2,方差为0,符合题意,且中位数是2,众数是2. 故选BD. 图5 第10题解析图 设异面直线B1P与A1D所成的角为θ,则 设M(1,0,m),m∈[0,1],则 即对于任意的M,存在点P使得AM⊥B1P,故D正确. 故选ABD. 11.设直线AB方程为x=my+t(t>0),A(x1,y1),B(x2,y2),2p=4,p=2, 所以y1+y2=4m,y1y2=-4t. 则x1+x2=m(y1+y2)+2t=4m2+2t, T为焦点时,t=1,x1+x2=4m2+2, 显然m=0时,|AB|min=4,A正确; 又D(-1,0),设过点D的切线方程是 y=k(x+1),k≠0, △=1-k2=0,k=±1. 直线AB方程为x=1,过焦点F(1,0),D正确. 故选ABD. 令g(x)=f′(x),则 则h(x)在[0,+∞)上单调递增. 则h(x)≥h(0)=1>0,则g′(x)>0. 则f′(x)在(0,+∞)上单调递增,故B正确; 令m(x)=f(x+x2)-f(x)-f(x2)(x>0), 则m′(x)=f′(x+x2)-f′(x)>0. 则m(x)在(0,+∞)上单调递增. 则m(x)>m(0)=f(x2)-f(0)-f(x2)=0. 则m(x1)>0. 所以f(x1+x2)>f(x1)+f(x2),故C正确; 令ω(x)=f′(x)(x-x1)-f(x)+f(x1),则 ω′(x)=g′(x)(x-x1)>0. 则ω(x)在(x1,+∞)上单调递增. 则ω(x)>ω(x1)=0. 则φ′(x)>0. 则φ(x)在(x1,+∞)上单调递增. 则φ(x2)<φ(x3). 则φ(x2)≤φ(x3),故D正确. 故选BCD. 16.记事件Ai表示从第i(i=1,2,…,n)个盒子里取出白球,则 17.(1)设{an}的公比为q(q>0),因为an+1+an+2=12an,即an·q+anq2=12an,且an≠0,可得q2+q-12=0,解得q=3或q=-4(舍去). 解得a1=1. 所以an=a1·qn-1=3n-1. (2)由(1)可得:bn=3n-1+(n-1)ln3, 所以Tn=b1+b2+b3+…+bn=(30+31+32+…+3n-1)+[1+2+3+…+(n-1)]ln3 在△ABC中,由余弦定理,得 将AB=3,BC=7代入并整理,得 AC2+3AC-40>0且AC2-6AC-40<0. 解得5 所以AC的取值范围是(5,10). (2)在△ABC中,由余弦定理可得, AC2=AB2+BC2-2AB·BC·cosα=9+49-2×3×7cosα=58-42cosα. 又因为△ACD为正三角形, 所以S四边形ABCD=S△ABC+S△ACD 所以∠ADB=∠CAB. 所以∠ADB+∠MAD=∠CAB+∠MAD=90°. 所以AC⊥BD. 即AM⊥BD,CM⊥BD. 所以PM⊥BD,CM⊥BD. 又PM∩CM=M,所以BD⊥平面PMC. 所以BD⊥PC. 由(1)BD⊥平面PMC,以M为坐标原点建立如图6所示的空间直角坐标系M-xyz, 图6 第19题解析图 取y1=sinθ,n=(0,sinθ,-cosθ),设平面PBC的一个法向量为m=(x2,y2,z2),则 (2)设M(x1,y1),N(x2,y2),MN:y=kx-1, 联立直线MN与椭圆C的方程可得 (2+3k2)x2-6kx-9=0. 所以2kx1x2=-3(x1+x2). 故直线QN的方程为 根据对称性,直线QN所过的定点在y轴上,不妨令x=0,则 =-2. 故直线QN过定点(0,-2). 21.(1)设每个芯片智能检测中安全检测、电池检测、性能检测三项指标达标的概率分别记为P1,P2,P3,并记芯片智能检测不达标为事件A. (3)设芯片人工抽检达标为事件B,工人在流水线进行人工抽检时,抽检一个芯片恰为合格品为事件C, 因此,该企业需对生产工序进行改良. 22.(1)当a=0时,f(x)=(x-1)ln(1-x)-x,其定义域为(-∞,1),f′(x)=ln(1-x),令f′(x)=ln(1-x)=0,得x=0. 当x∈(-∞,0)时,f′(x)>0,故f(x)在(-∞,0)上单调递增;当x∈(0,1)时,f′(x)<0,故f(x)在(0,1)上单调递减. 因此,函数f(x)的单调递增区间为(-∞,0),单调递减区间为(0,1). (2)令g(x)=f′(x)=ln(1-x)+asinx,则 因为x∈(0,1),则1-x∈(0,1),cosx∈(0,1),则(1-x)cosx∈(0,1). 当a≤1时,则a(1-x)cosx-1<0,故g′(x)<0,从而g(x)在(0,1)上单调递减. 而g(0)=0,故当x∈(0,1)时,g(x) 即f′(x)在区间(0,1)上无零点. 当a>1时,令h(x)=a(1-x)cosx-1,则 h′(x)=-a[cosx+(1-x)sinx]. 因为x∈(0,1),则cosx+(1-x)sinx>0. 从而h′(x)<0. 即h(x)在(0,1)上单调递减. 而h(0)=a-1>0,h(1)=-1<0,因此存在唯一的x0∈(0,1),使得h(x0)=0,并且当x∈(0,x0)时,h(x)>0;当x∈(x0,1)时,h(x)<0. 即当x∈(0,x0)时,g′(x)>0,当x∈(x0,1)时,g′(x)<0. 故当x∈(0,x0)时,g(x)单调递增,当x∈(x0,1)时,g(x)单调递减.而g(0)=0,故g(x0)>0. 取N=1-e-2a∈(0,1),当x>N时,g(x)=ln(1-x)+asinx 所以存在唯一的m∈(x0,1),使得g(m)=0,即f′(x)在区间(0,1)上有唯一零点. 综上所述,当a>1时,f′(x)在(0,1)上有唯一的零点; 当a≤1时,f′(x)在(0,1)上没有零点. (3)由(2)可得,当a≤1时,ln(1-x)+asinx<0在(0,1)上恒成立. 以下证明不等式: 则m(x) 即有xcosx

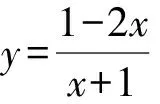
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
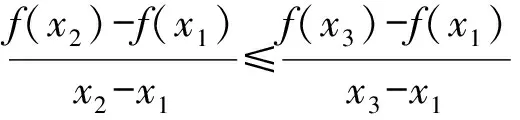
三、填空题:本题共4小题,每小题5分,共20分.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.