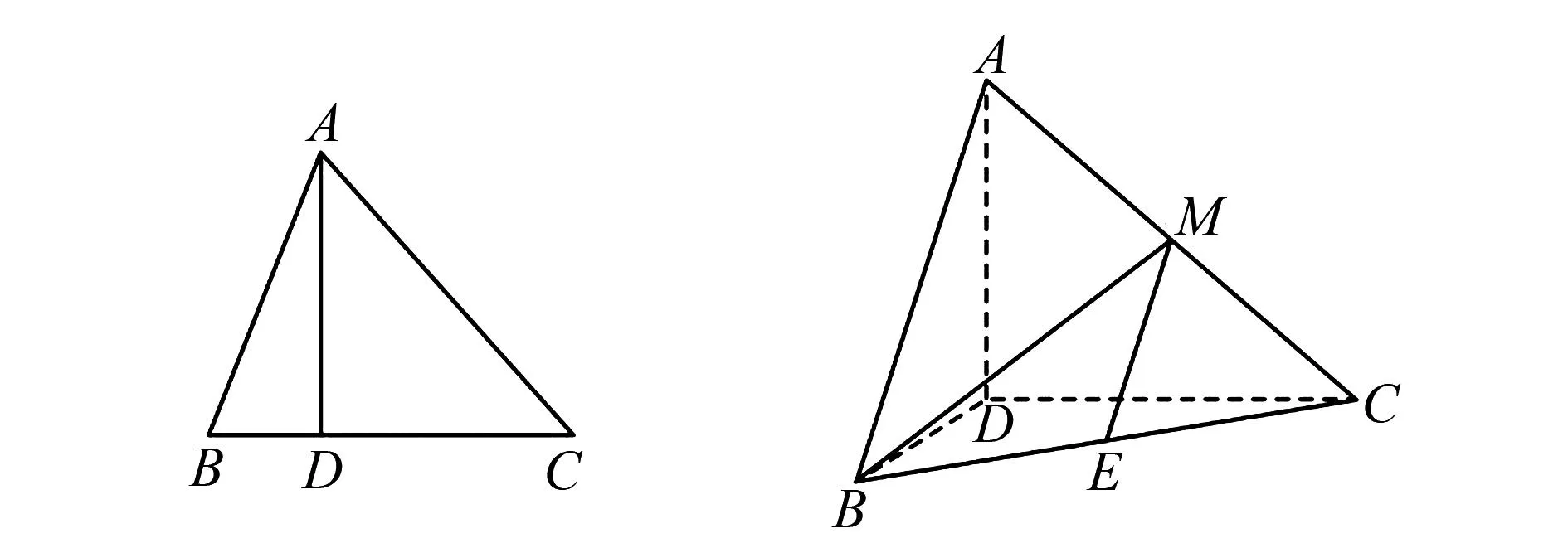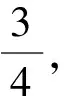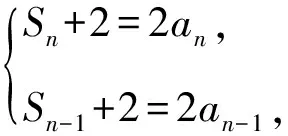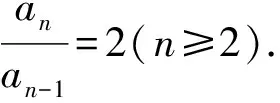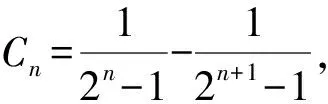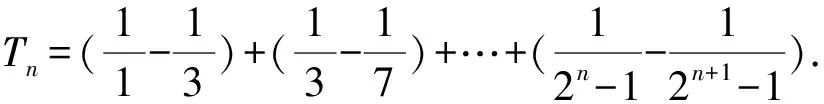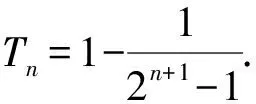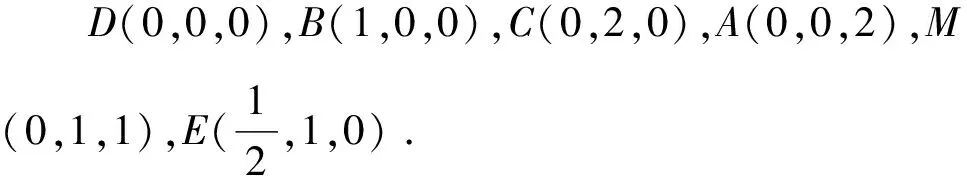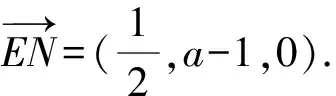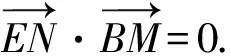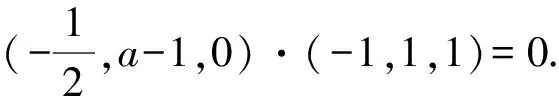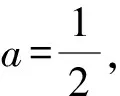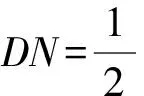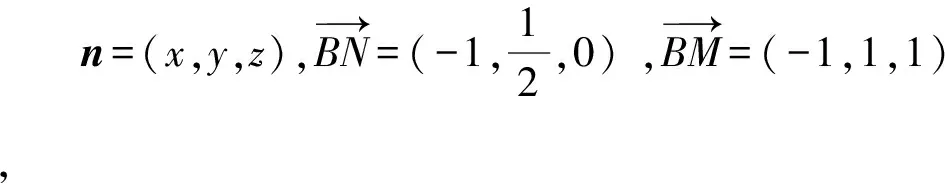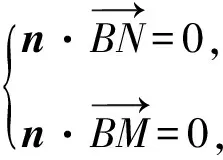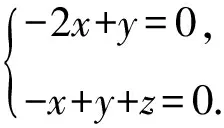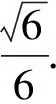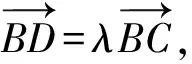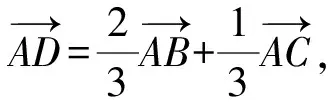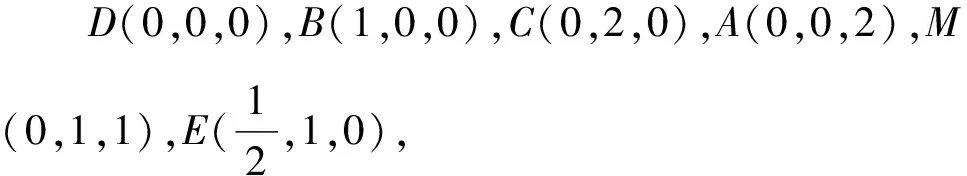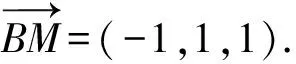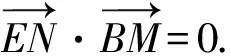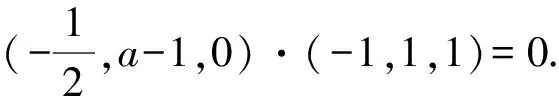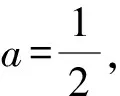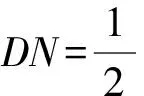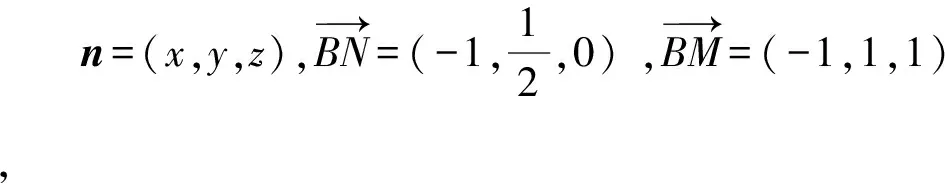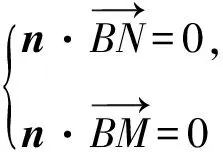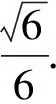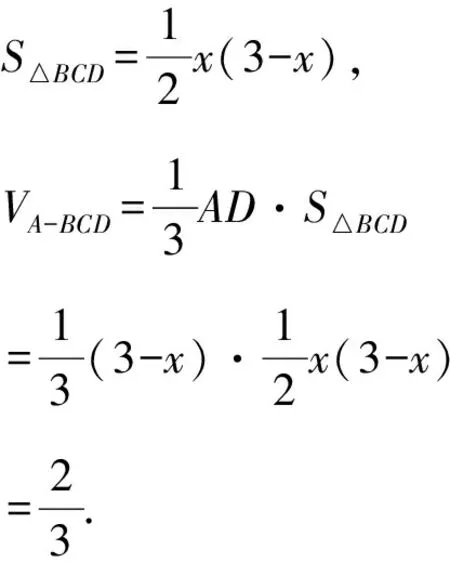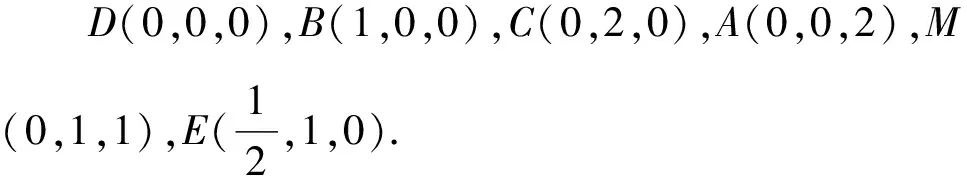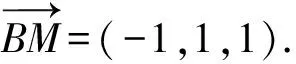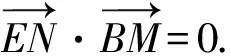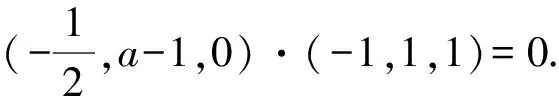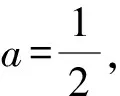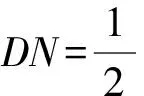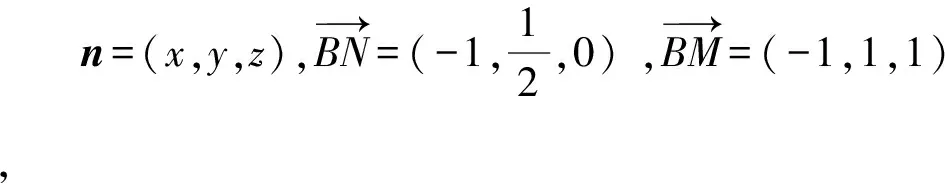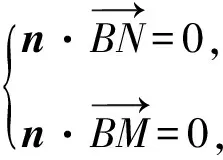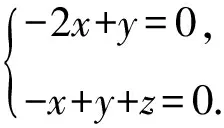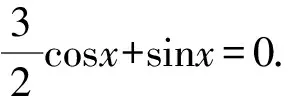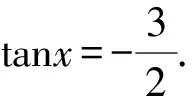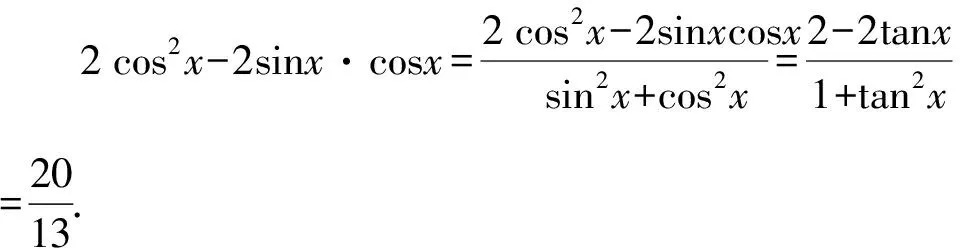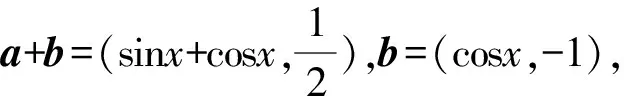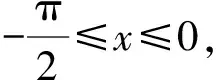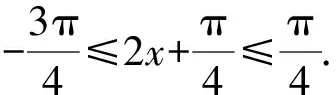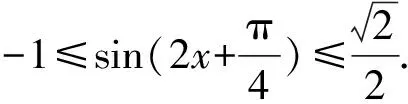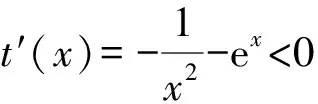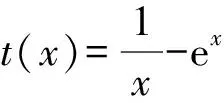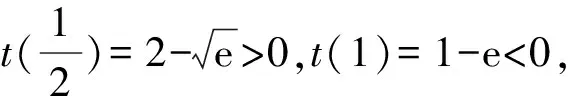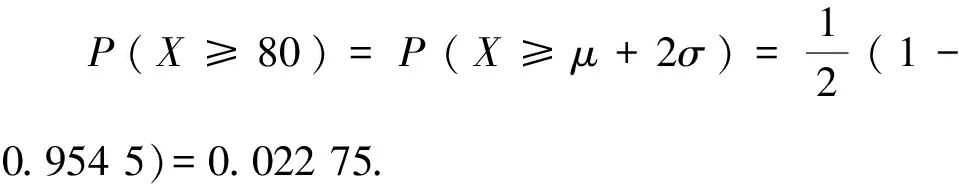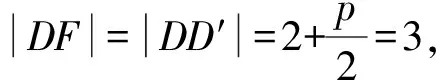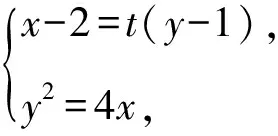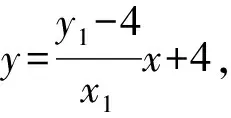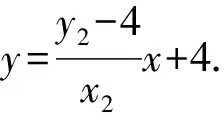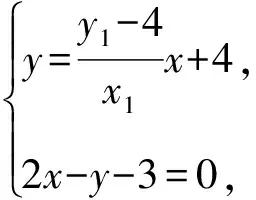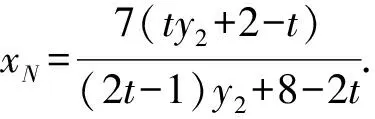2024年新高考数学模拟卷(二)
李春林
(甘肃省天水市第九中学,甘肃 天水 741020)
(河南、山西、江西、安徽、甘肃、青海、内蒙古、黑龙江、吉林、宁夏、新疆、陕西)
第Ⅰ卷(选择题)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.

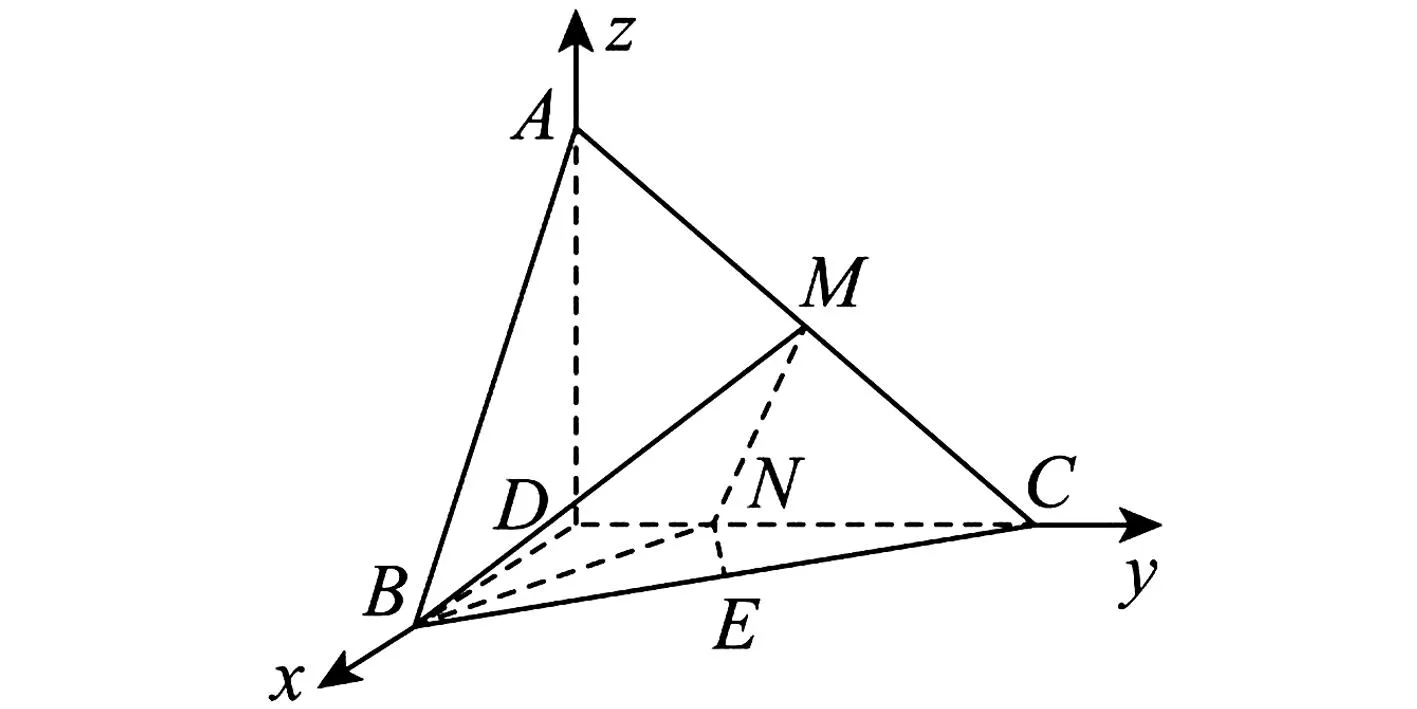
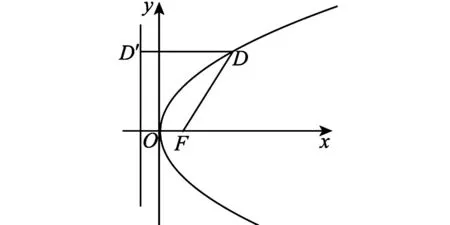
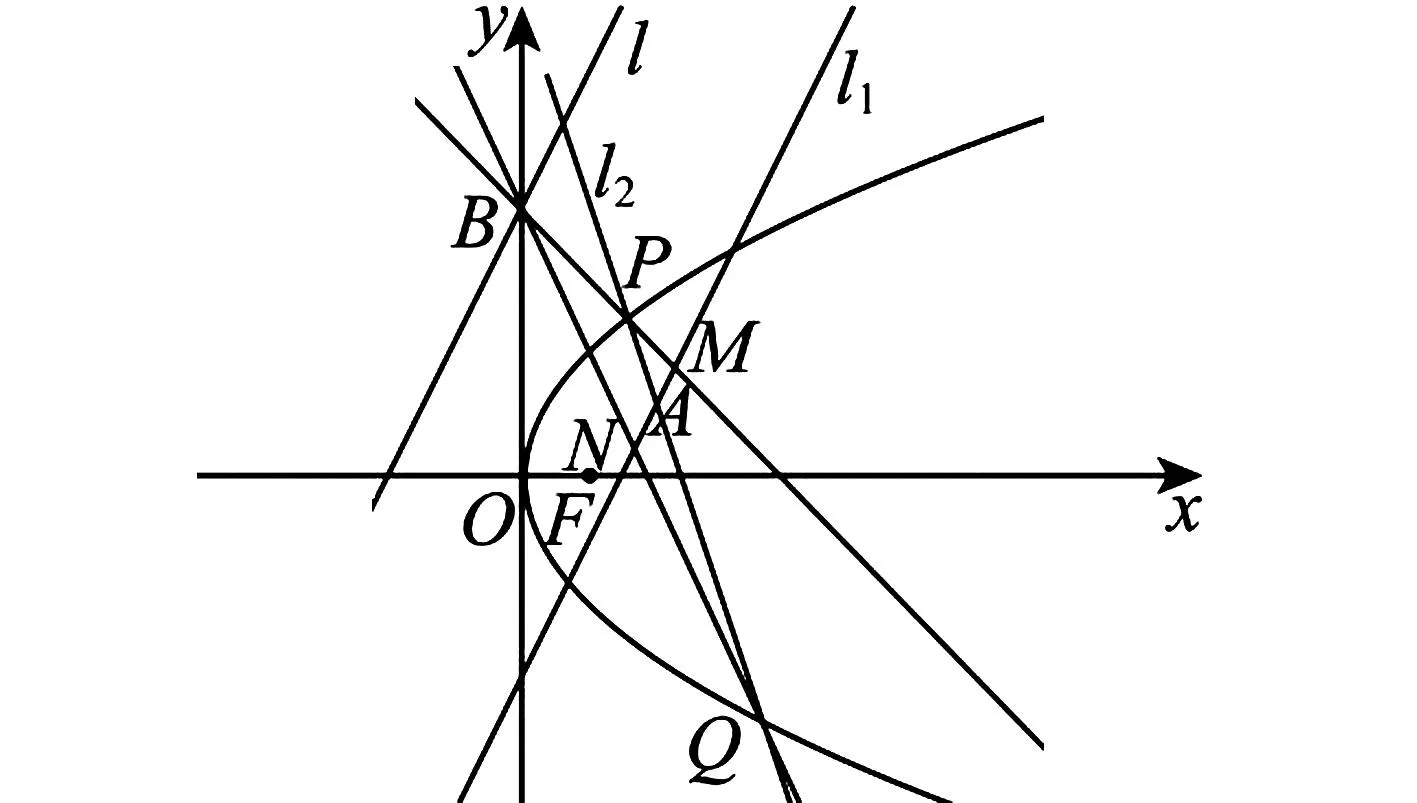
A.{x|0 C.{x|1 2.已知复数-3+2i是方程2x2+12x+q=0的一个根,则实数q的值是( ). A.0 B.8 C.24 D.26 A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分又不必要条件 4.已知向量a,b满足(a-b)·b=2,且b=(-1,1),则向量a在向量b上的投影向量为( ). A.(2,2) B.(-2,2) C.(1,1) D.(-1,1) 6.有三个数:a=20.5,b=sin1,c=log23,大小顺序正确的是( ). A.c>a>bB.a>c>bC.a>b>cD.b>a>c 8.2023年杭州亚运会于9月23日至10月8日举办,组委会将甲、乙、丙、丁4名志愿者随机派往黄龙体育中心、杭州奥体中心、浙江大学紫金港校区三座体育馆工作,每座体育馆至少派1名志愿者,A表示事件“志愿者甲派往黄龙体育中心”;B表示事件“志愿者乙派往黄龙体育中心”;C表示事件“志愿者乙派往杭州奥体中心”,则( ). A.事件A与B相互独立 B.事件A与C为互斥事件 9.下列结论正确的有( ). A.若随机变量ξ,η满足η=2ξ+1,则D(η)=2D(ξ)+1 C.若线性相关系数|r|越接近1,则两个变量的线性相关性越强 11.定义在R上的函数f(x)满足f(2-x)=f(x),f(1)=2,f(3x+2)为奇函数,函数g(x)(x∈R)满足g(x)=-g(4-x),若y=f(x)与y=g(x)恰有2 023个交点(x1,y1),(x2,y2),…,(x2023,y2023),则下列说法正确的是( ). A.f(2 023)=2 B.x=1为y=f(x)的对称轴 12.在正方体ABCD-A1B1C1D1中,AB=2,G为C1D1的中点,点P在线段B1C上运动,点Q在棱C1C上运动,M为空间中任意一点,则下列结论正确的有( ). A.直线BD1⊥平面A1C1D 14.已知(1-2x)n的二项展开式中第3项与第10项的二项式系数相等,则展开式中含x的系数为____. 16.若两曲线y=x2-1与y=alnx-1存在公切线,则正实数a的取值范围是____. 17.在数列{an}中,Sn为数列{an}的前n项和,且满足Sn+2=2an. (1)求数列{an}的通项公式; 如图1所示,在△ABC中,∠ACB=45° ,BC=3,过点A作AD⊥BC,垂足D在线段BC上,沿AD将△ABD折起,使∠BDC=90° (如图2),点E,M分别为棱BC,AC的中点. 图1 第18题图(a) (1)求证:CD⊥ME; (2)已知____,试在棱CD上确定一点N,使得EN⊥BM,并求二面角M-BN-C的余弦值. 注:如果选择多个条件分别解答,按第一个解答计分. (1)当a∥b时,求2cos2x-2sinx·cosx的值; 20.已知函数f(x)=-x+lnx,g(x)=xex-2x-m. (1)求函数f(x)的单调区间及极值; (2)若f(x)≤g(x)恒成立,求实数m的取值范围. 21.某地区举行专业技能考试,共有8 000人参加,分为初试和复试,初试通过后方可参加复试.为了解考生的考试情况,随机抽取了100名考生的初试成绩绘制成如图3所示的样本频率分布直方图. 图3 样本频率分布直方图 (1)根据频率分布直方图,估计样本的平均数; (2)若所有考生的初试成绩近似服从正态分布N(μ,σ2),其中μ为样本平均数的估计值,σ≈9,试估计所有考生中初试成绩不低于80分的人数; 附:若随机变量X服从正态分布N(μ,σ2),则P(μ-σ 22.已知抛物线C:y2=2px(p>0)的焦点为F,点D(2,y0)是抛物线上一点,且|DF|=3. (1)求抛物线C的方程; (2)设直线l:2x-y+4=0,点B是l与y轴的交点,过点A(2,1)作与l平行的直线l1,过点A的动直线l2与抛物线C相交于P,Q两点,直线PB,QB分别交直线l1于点M,N,证明:|AM|=|AN|. 参考答案 1.B 2.D 3.A 4.B 5.D 6.A 7.B 8.D 9.CD 10.ABD 11.BCD 12.ACD 17.(1)当n=1时,a1+2=2a1,解得a1=2. 得Sn-Sn-1=2(an-an-1). 即an=2(an-an-1),易知an-1≠0. 所以{an}是以a1=2为首项,以2为公比的等比数列. 故an=2n. 18.(1)因为CD⊥AD,CD⊥BD,AD∩BD=D,AD,BD⊂平面ABD, 所以CD⊥平面ABD. 因为AB⊂平面ABD, 所以CD⊥AB. 又M,E分别为AC,BC的中点, 所以ME∥AB. 所以CD⊥ME. 图4 第18题解析图 设AD=CD=x,在Rt△ABD中, 解得x=2, 所以BD=1. 因为EN⊥BM, 令x=1,得y=2,z=-1 ,则n=(1,2,-1). 取平面BNC的一个法向量m=(0,0,1),则 又二面角M-BN-C的平面角为锐角, 设N(0,a,0),0≤a≤2 ,则 因为EN⊥BM, 令x=1,得y=2,z=-1 ,则n=(1,2,-1). 取平面BNC的一个法向量m=(0,0,1),则 又二面角M-BN-C的平面角为锐角, 方案三:选③,设BD=x(0 因为AD⊥CD,∠ACD=45°, 所以△ADC为等腰直角三角形. 所以AD=CD=3-x. 在三棱锥A-BCD中,AD⊥DC,AD⊥BD,且BD∩DC=D,BD,DC⊂平面BCD, 所以AD⊥平面BCD. 化简,得(x-1)2(x-4)=0, 解得x=1或x=4(舍去). 设N(0,a,0),0≤a≤2 ,则 因为EN⊥BM, 令x=1,得y=2,z=-1 ,则n=(1,2,-1). 取平面BNC的一个法向量m=(0,0,1), 又二面角M-BN-C的平面角为锐角, 所以f(x)=(a+b)·b 所以x=1是f(x)的极大值点,无极小值点. 所以f(x)的极大值为f(1)=-1,无极小值. (2)设h(x)=f(x)-g(x)=lnx-xex+x+m,x∈(0,+∞),则 因此,当0 所以当m≤1时,f(x)≤g(x)恒成立,即实数m的取值范围是(-∞,1]. 21.(1)由题意得,样本平均数的估计值为 (40×0.010+50×0.020+60×0.030+70×0.024+80×0.012+90×0.004)×10=62. (2)学生初试成绩X服从正态分布N(μ,σ2),其中μ=62,σ≈9,则 μ+2σ=62+2×9=80. 所以估计初试成绩不低于80分的人数为0.022 75×8 000=182人. 图5 第22题第(1)问解析图 所以抛物线C的方程为y2=4x. (2)如图6,直线l:2x-y+4=0,令x=0得y=4,所以点B(0,4). 因为直线l1平行于直线l:2x-y+4=0,且过点A(2,1),所以直线l1:2x-y-3=0. 图6 第22题第(2)问解析图 设直线l2:x-2=t(y-1), y2-4ty+4t-8=0. 所以△=16(t2-t+2)>0. 设点P(x1,y1),Q(x2,y2), 由韦达定理可得 y1+y2=4t,y1y2=4t-8. 因为xA=2, 所以xM+xN=2xA. 即A是线段MN的中点. 所以|AM|=|AN|.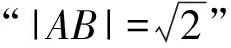
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
第Ⅱ卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分.
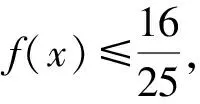
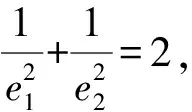
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.