对一道解析几何模考题的探究

钟国城

(广东省梅县东山中学,广东 梅州 514017)

解析几何是高考的热点与难点内容,解析几何解答题通常处于压轴题的位置,难度较大,学生在求解时难于求解出答案.本文将通过一道解析几何模考题的多角度探究,帮助学生突破解析几何障碍,提升解题能力.

1 题目呈现

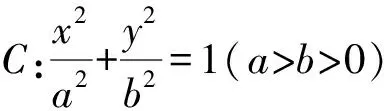
(1)求C的方程;

(2)直线l:y=k(x-1)(k≠0)与C相交于A,B两点,过C上的点P作x轴的平行线交线段AB于点Q,直线OP的斜率为k′(O为坐标原点),△APQ的面积为S1,△BPQ的面积为S2.若|AP|·S2=|BP|·S1,判断k·k′是否为定值?并说明理由.

2 总体分析

本题第(1)问考查椭圆的标准方程,根据题意建立有关a,b,c的方程组,求解方程组即可得到答案,属于常规问题;第(2)问利用直线与椭圆的位置关系研究有关斜率的定值问题,此问可以多视角解答,涉及三角形面积、角平分线定理、弦长公式等知识,重点考查化归与转化、方程等数学思想,全面考查学生的数学运算、逻辑推理等数学核心素养.本文将对第(2)问进行多角度探究,以飨读者.

3 试题解答

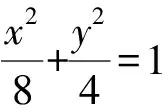
以下重点探讨第(2)问,解决此问的关键在于条件|AP|·S2=|BP|·S1的转化,可以从四个方面入手.

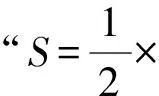
解法1 设P(x0,y0),A(x1,y1),B(x2,y2),直线AP与BP的斜率分别为k1与k2(k1≠k2),则

因为|AP|·S2=|BP|·S1,

所以|AP|·|y2-y0|=|BP|·|y1-y0|.

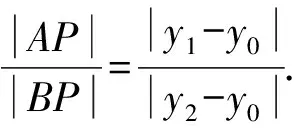
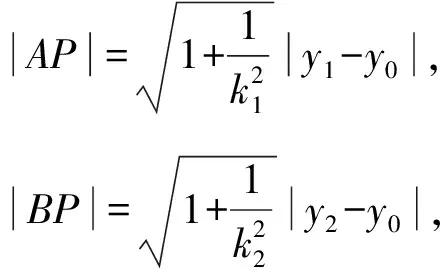
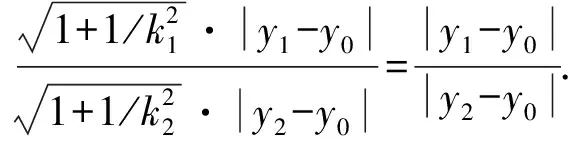
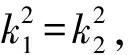
即k1+k2=0.

评注此法利用弦长公式与面积公式将条件坐标化,进而转化出斜率之间的关系,让解题目标非常明确,体现了解析几何问题的本质.

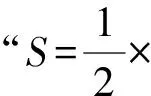
解法2 设P(x0,y0),A(x1,y1),B(x2,y2),点P到直线l的距离为h,则

因为|AP|·S2=|BP|·S1,

所以|AP|·|BQ|=|BP|·|AQ|.

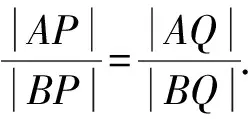
(方向1)由角平分定理,得PQ为∠APB的角平分线,则∠APQ=∠BPQ.

所以k1=-k2.

即k1+k2=0.

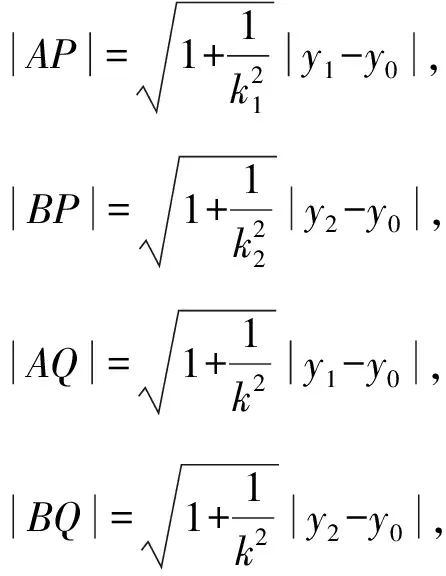
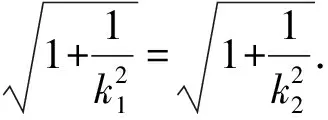
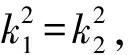
即k1+k2=0.

评注此法方向1使用角平分线定理进行处理,方便快捷,说明解析几何的问题本质还是属于几何问题,使用相关几何性质求解问题能起到事半功倍的效果.方向2使用弦长公式进行求解,符合解析几何问题的特点,属于通性通法.

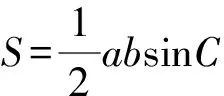
解法3 设P(x0,y0),A(x1,y1),B(x2,y2),直线AP与BP的斜率分别为k1与k2(k1≠k2),则

因为|AP|·S2=|BP|·S1,

所以sin∠APQ=sin∠BPQ.

即∠APQ=∠BPQ,

故k1=-k2.

即k1+k2=0.

评注此法最为直接,根据两个三角形的特点,利用相关公式,将条件直接转化为夹角关系,进而得到斜率之间的关系,体现了灵活运用知识解决问题的能力.

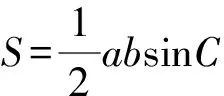
解法4 设P(x0,y0),A(x1,y1),B(x2,y2),直线AP与BP的斜率分别为k1与k2(k1≠k2),则

因为∠AQP+∠BQP=π,

即sin∠AQP=sin∠BQP,且

|AP|·S2=|BP|·S1,

所以|AP|·|BQ|=|BP|·|AQ|.

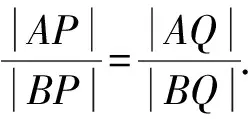
以下同解法2.

评注此法利用两个三角形的互补角关系进行转化,对比解法2与解法3,虽无更加便捷,但给解决此类问题提供了另一种有效方式,值得我们认真体会.

通过以上四种思路,将条件|AP|·S2=|BP|·S1转化为条件k1+k2=0,让解题方向更加明确.下面将从两个角度对条件k1+k2=0进行探究.

思路1 利用韦达定理进行求解.

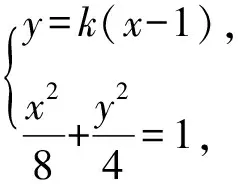
(1+2k2)x2-4k2x+2k2-8=0.

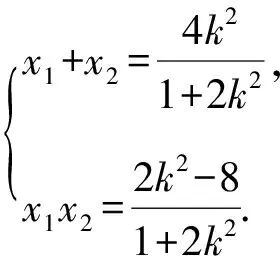
因为k1+k2=0,

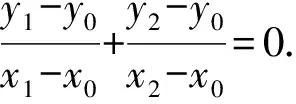
所以(kx1-k-y0)(x2-x0)+(kx2-k-y0)(x1-x0)=0.

即2kx1x2-(kx0+y0+k)(x1+x2)+2x0(k+y0)=0.

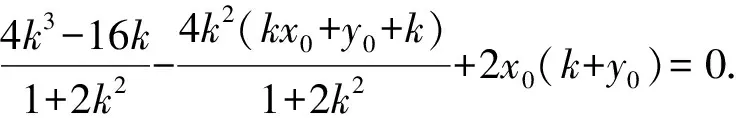
故2y0(x0-1)k2+(x0-8)k+x0y0=0.(*)

因为点P在椭圆C上,

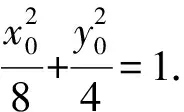
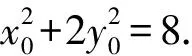
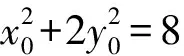
即(2y0k-x0)[(x0-1)k-y0]=0.

因为点P不在直线l上,

所以y0≠k(x0-1).

即k(x0-1)-y0≠0.

故2y0k-x0=0.

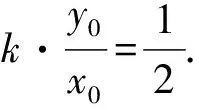
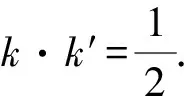
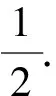
评注此法为通法,难点在于含参多、计算量大,尤其是后面的因式分解技巧性较强,因此,在平时的练习中,需多总结一些优化运算的方法,熟练常规运算,提高运算能力.

思路2 利用“齐次化”进行处理.

解法2 设直线l的方程为

m(x-x0)+n(y-y0)=1,

(△)

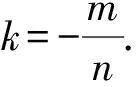
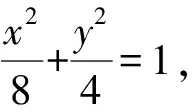
因为点P在椭圆C上,

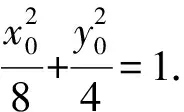
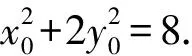
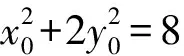
2(y-y0)2+2x0(x-x0)+4y0(y-y0)+(x-x0)2=0.

所以2(y-y0)2+[2x0(x-x0)+4y0(y-y0)]·[m(x-x0)+n(y-y0)]+(x-x0)2=0.

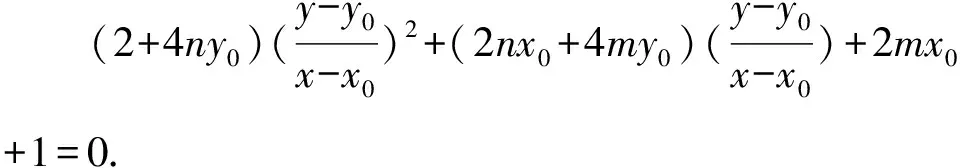
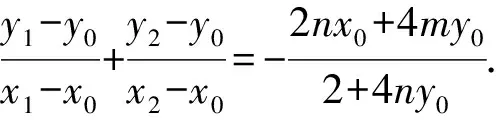
因为k1+k2=0,

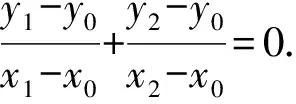
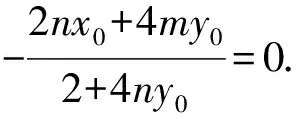
即2nx0+4my0=0.

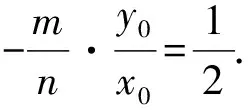
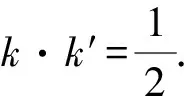
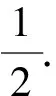
评注此法为巧法,通常解析几何问题涉及斜率之和或之积时,均可使用“齐次化”处理,但使用此法时需注意直线方程的形式以及曲线方程的变形,都要符合这种方法的要求.

4 试题推广

根据上述求解过程,将椭圆方程一般化,同时推广到双曲线、抛物线、圆,得到以下几个结论.

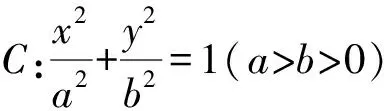
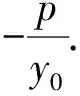
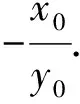
以上结论的证明过程与试题求解过程类似,在此不再赘述.

5 结束语

解析几何问题包罗万象,对于基础知识、基本方法、基本思想学生容易掌握到位.但解析几何大题涉及许多关联知识和一些技巧性较强的方法,学生很难突破.解析几何是高考的热点与难点内容,因此,在平时的教学中,必须舍得花时间和精力去深入研究,总结方法与规律,积累基本经验,开拓解题思路,不断提升解题技能.解析几何中涉及斜率之和或之积问题入口很宽,求解方法多样,对加深理解解析几何的本质、提升数学思维与核心素养大有裨益[1].