基于核心素养的一道高考压轴题的多种解法
刘彦永
(大连市第二十四中学 ,辽宁 大连 116021)
从双基教学的产生到情感态度价值观、学生学科核心素养理念的提出、研究和实施,教育教学目标的实施逐步具体、明确、可操作[1].数学核心素养只有在解决问题中才能体现出来,没有具体的情境,就无法判断一个人的数学素养的高低.2022年高考全国甲卷理科第21题充分体现了数学的六大核心素养(数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析),对深化课程改革、教材更新、引领数学教学等起到了积极的导向作用.
1 试题呈现
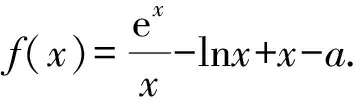
(1)若f(x)≥0,求a的取值范围;
(2)证明:若f(x)有两个零点x1,x2,则x1x2<1.
2 试题分析
本题已知条件简明扼要,问题却又内涵丰富.第(1)问是已知不等式恒成立求参数的范围,第(2)问本质是函数的极值点偏移问题.既考查学生的数形结合、分类讨论、函数方程和等价转化等数学思想,又考查学生分析问题和解决问题的能力.考查层次分明、区分度较高,能使学生充分展示理性思维的广度和深度,是一道综合考查核心素养的绝佳好题[2].
3 试题解答
3.1 第(1)问解析
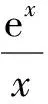
所以函数的定义域是(0,+∞).
因为ex≥ex和lnx≤x-1,
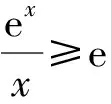
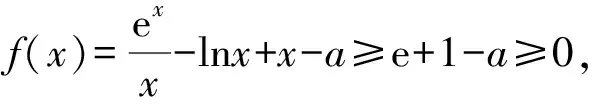
解得a≤e+1.
即a的取值范围是(-∞,e+1].
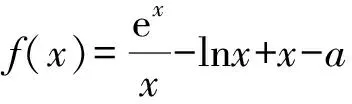
令f′(x)=0,得x=1,当x∈(0,1)时,f′(x)<0,f(x)单调递减;
当x∈(1,+∞)时,f′(x)>0,f(x)单调递增.
故f(x)≥f(1)=e+1-a≥0,
解得a≤e+1.
即a的取值范围是(-∞,e+1].
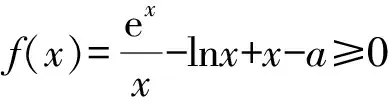
令t=x-lnx且t∈[1,+∞),则有
et+t-a≥0.
记h(t)=et+t-a,t∈[1,+∞),
则h(t)单调递增.
故有[h(t)]min=h(1)=e+1-a≥0,解得a≤e+1.
即a的取值范围是(-∞,e+1].
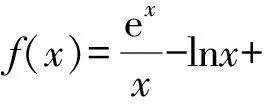
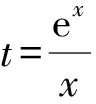
t+lnt-a≥0.
记h(t)=t+lnt-a,t∈[e,+∞),
则h(t)单调递增.
故有[h(t)]min=h(e)=e+1-a≥0,解得a≤e+1.
即a的取值范围是(-∞,e+1].
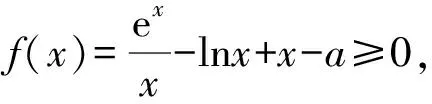
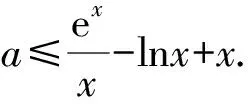
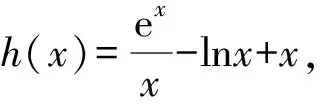
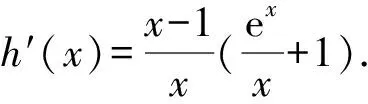
当x∈(0,1)时,h′(x)<0,h(x)单调递减;
当x∈(1,+∞)时,h′(x)>0,h(x)单调递增.
故[h(x)]min=h(1)=e+1,解得a≤e+1.
即a的取值范围是(-∞,e+1].
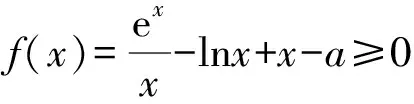
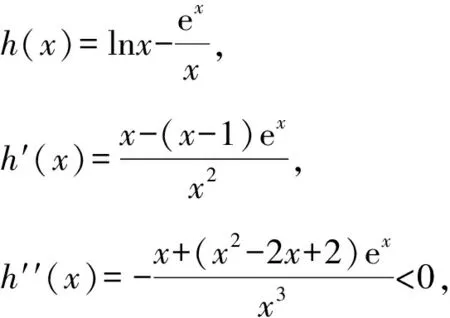
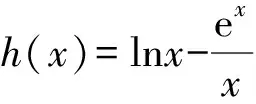
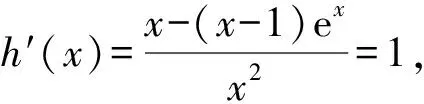
即a的取值范围是(-∞,e+1].
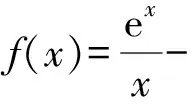
h(x)=lnx-x+a,
[g(x)]min=g(1)=e,
[h(x)]max=h(1)=-1+a,
故有a≤e+1.
即a的取值范围是(-∞,e+1].
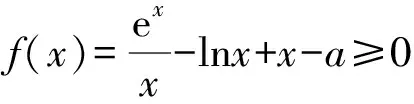
充分性:当a≤e+1时,
综上所述,a的取值范围是(-∞,e+1].
点评问题(1)的本质是含参不等式恒成立问题,破解策略主要有放缩法(解法1)、最值分析法(解法2)、换元法(解法3,4)、参数变量分离法(解法5)、数形结合法(解法6,7)、必要性探路法(解法8)、分类讨论法、基本不等式法、齐次化法、判别式法、构造函数法等.
3.2 第(2)问解析
由题(1)知,f(x)的一个零点小于1,一个零点大于1,不妨设0 因为f(x2)=f(x1), 故h(x)在(0,1)上单调递增,且h(1)=0. 因为f(x2)=f(x1), 则结合ex≥ex知 故h(x)在(0,1)上单调递增,且h(1)=0. 从而x1x2<1. 因为f(x2)=f(x1), g(x)在(0,1)上单调递减,且g(1)=0,故g(x)>0. 记h(t)=et+t-a,t∈[1,+∞),则h(t)单调递增. 因为f(x)有两个零点x1,x2,所以h(t)=et+t-a有零点t0>1,且t0=x1-lnx1=x2-lnx2. 等价于g(x)=x-lnx有两个不同零点x1,x2. 因为g(x)在(1,+∞)上单调递增, 因为g(x2)=g(x1), 因为f(x)有两个零点x1,x2,所以h(t)=et+t-a有零点t0>1,且t0=x1-lnx1=x2-lnx2. 等价于g(x)=x-lnx有两个不同零点x1,x2. 要证x1x2<1, 因为g(x1)=g(x2), 故p(x2) 记h(t)=et+t-a,t∈[1,+∞),则h(t)单调递增. 因为f(x)有两个零点x1,x2,所以h(t)=et+t-a有零点t0>1,且t0=x1-lnx1=x2-lnx2. 等价于g(x)=x-lnx有两个不同零点x1,x2. 构造函数g(x)=x-lnx的逼近函数 则q(x)=p(x)-g(x) 其中x∈(0,+∞), 故q(x)在(0,+∞)上单调递减. 因为q(1)=0,所以x∈(0,1)时,q(x)>0,x∈(1,+∞)时,q(x)<0, >q(1)=0, 故ln2x2 即lnx2<-lnx1. 也就是lnx2+lnx1=lnx1x2<0. 所以x1x2<1. 因为f(x)有两个零点x1,x2,所以h(t)=et+t-a有零点t0>1,且t0=x1-lnx1=x2-lnx2. 所以x1x2<1. 因为f(x)有两个零点x1,x2,所以h(t)=et+t-a有零点t0>1,且t0=x1-lnx1=x2-lnx2, 即x2-x1=lnx2-lnx1. 故g(n)在(1,+∞)上单调递减. 因为g(1)=0, 从而x1x2<1. 因为f(x)有两个零点x1,x2,所以h(t)=et+t-a有零点t0>1,且t0=x1-lnx1=x2-lnx2. 即x2-x1=lnx2-lnx1. 则g(n)在(1,+∞)上单调递减. 因为f(x)有两个零点x1,x2,所以h(t)=et+t-a有零点t0>1,且t0=x1-lnx1=x2-lnx2, 即x2-x1=lnx2-lnx1. 则g(n)在(0,+∞)上单调递增. 点评问题(2)的本质是极值点偏移问题,破解策略主要有构造函数法(解法1-6)、对数平均不等式法(解法7)、换元法(解法8-10).构造函数的技巧和方法非常多,基于不同的角度就可以构建不同的函数,限于篇幅,本文不再赘述.换元常用的策略是差值换元和比值换元,这都需要通过实战解题不断演练变熟练. 上述两个问题的解答都充分体现了数学核心素养对解题的思路引领.各个解法建立了对应的数学模型,通过逐步深入的逻辑推理和数据分析、数学运算简化问题,最后使问题得以顺利解决. 发展学生的数学核心素养,有利于学生学会用数学的眼光观察现实世界,用数学的思维思考现实世界,用数学的语言表达现实世界.“一题多解”正是提高数学核心素养的有效策略.在实际教学过程中,我们应抓住具有多解的好题,让学生去感受、体验、思考、总结和反思,进而体会到灵活应用所学知识、思想和方法创造性地解决问题的美妙感觉,培养学习的兴趣和提高数学核心素养.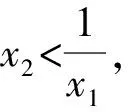
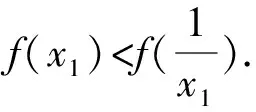
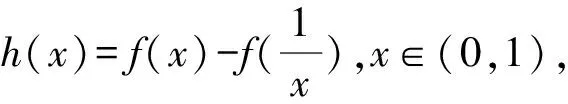
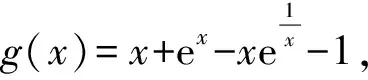
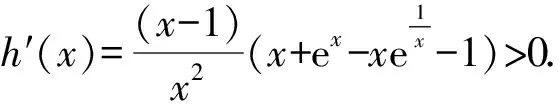
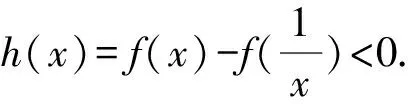
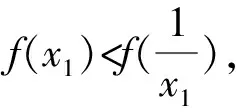
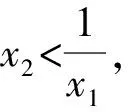
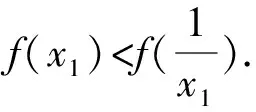
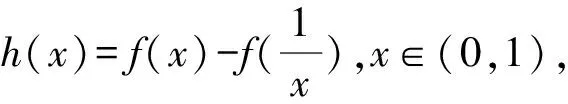
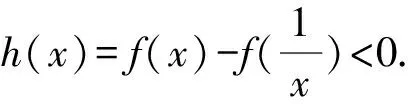
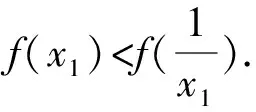
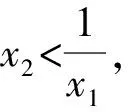
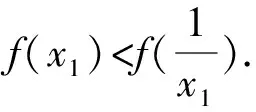
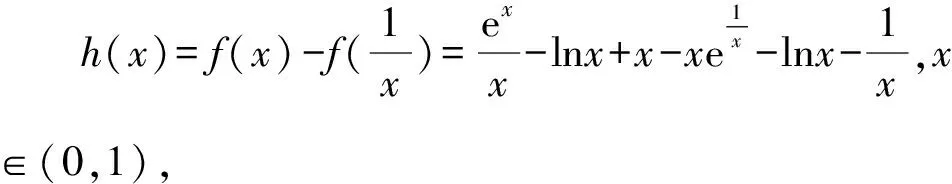
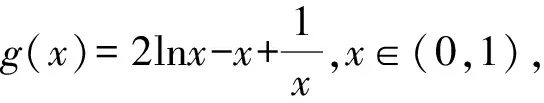
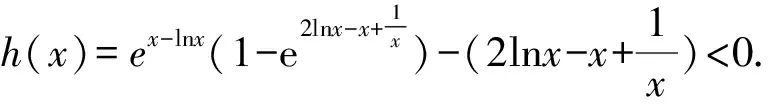
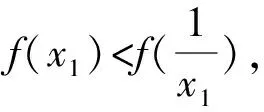
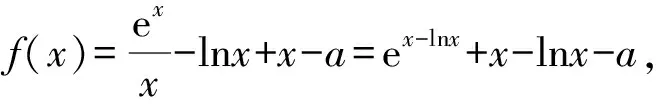
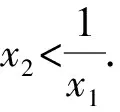
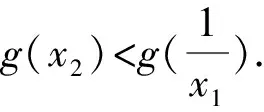
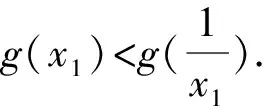
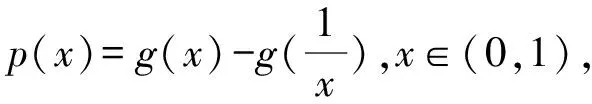
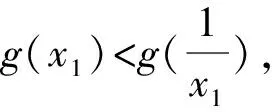
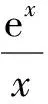
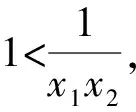
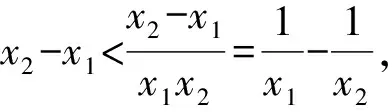
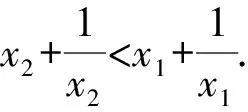
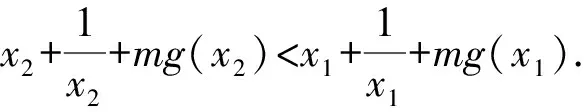
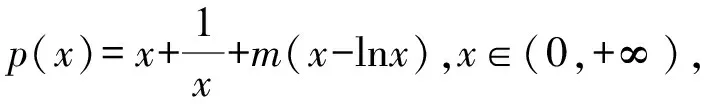
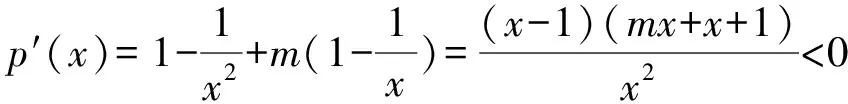
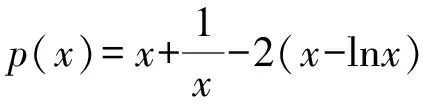
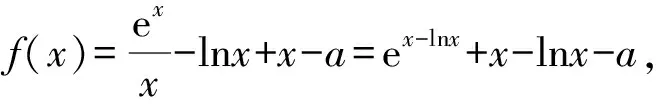
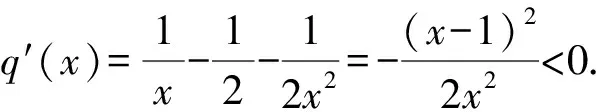
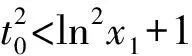
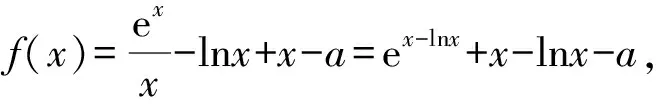
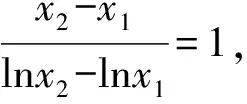
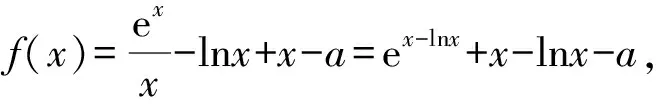
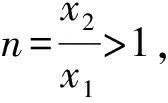
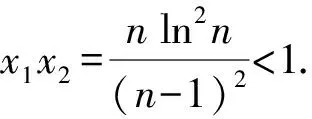
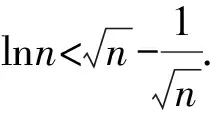
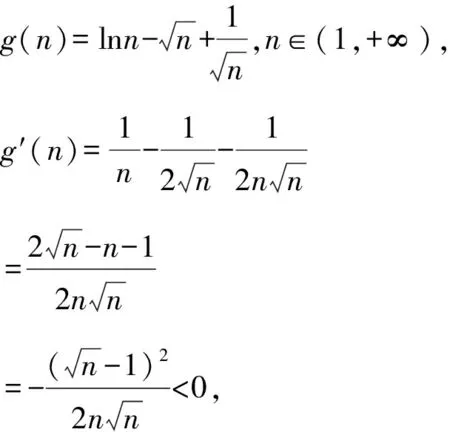
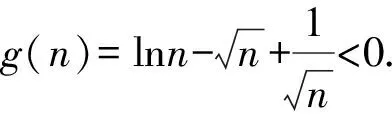
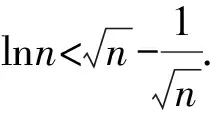
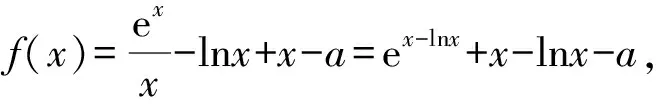
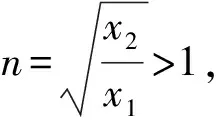
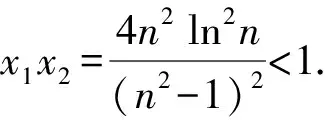
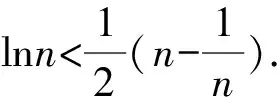
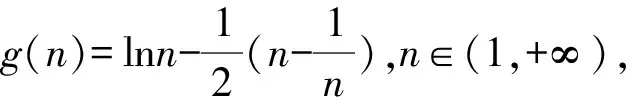
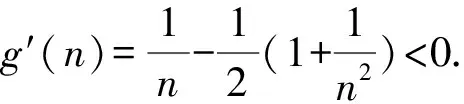
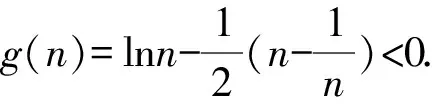
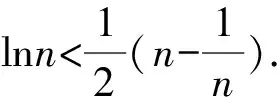
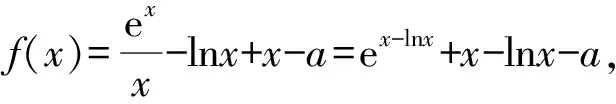
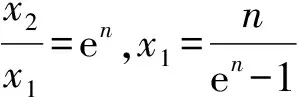
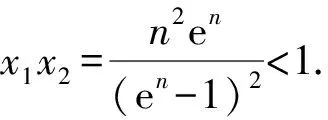
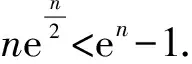
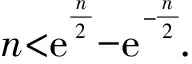
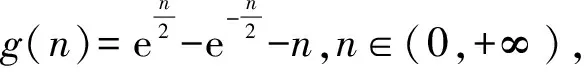
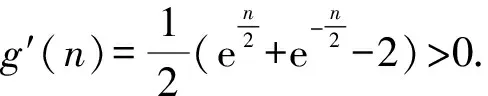
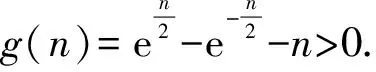
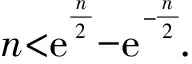
4 结束语

