对2022年一道高考题的解法研究及推广
刘大鹏
(辽宁省黑山县第一高级中学,辽宁 锦州 121400)
2022年全国新高考Ⅱ卷第22题作为全卷的压轴题,考查了利用导数研究函数的单调性;含参不等式恒成立时,求参数的取值范围;与数列求和有关的不等式证明.这道题综合性强,难度大,有很高的研究价值,也很有区分度,是难得的一道好题.文章对第(3)问给出了5种证明方法和4个推广命题,这是本文的亮点.
1 高考题再现
题目(2022年全国新高考Ⅱ卷第22题)已知函数f(x)=xeax-ex.
(1)当a=1时,讨论f(x)的单调性;
(2)当x>0时,f(x)<-1,求a的取值范围;
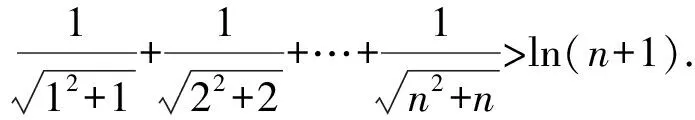
2 解法展示
解析(1)当a=1时,f(x)=(x-1)ex,
f′(x)=ex+(x-1)ex=xex,所以x∈(-∞,0),f′(x)<0,f(x)单调递减;x∈(0,+∞),f′(x)>0,f(x)单调递增.
(2)构造函数
g(x)=f(x)+1=xeax-ex+1,(x≥0),
g(0)=0,
g′(x)=eax+axeax-ex,
g′(0)=0,g″(x)=aeax+aeax+a2xeax-ex=a(2+ax)eax-ex,
g″(0)=2a-1,
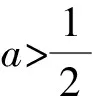
所以∃x0>0,使x∈(0,x0),g′(x)>0,g(x)单调递增,g(x0)>g(0)=0,不符合题意.

g′(x)=eax+ln(1+ax)-ex
所以g(x)在(0,+∞)单调递减,g(x) (3)证法1 构造函数 所以t(x)在[1,+∞)单调递减. 所以t(x)≤t(1)=0. 证法2 构造函数 所以p(x)在(0,+∞)单调递增. 所以p(x)>p(0)=0. 证法3 构造函数 >0, 所以w′(x)在(0,+∞)上单调递增, 所以w′(x)<0. 所以w(x)在(0,+∞)上单调递减[1]. =0, (*) 所以q′(x)>0,q(x)在(0,+∞)单调递增, =1. 所以q(x)<1. 将x分别代入1,2,3,…,n,相加,得 证法4 构造数列 证法5 (数学归纳法) 所以,当n=k+1时,命题也成立. 证明在证法3中已证w(x)>0,即 将x分别代入1,2,3,…,n,相加即可. u(x)在(0,+∞)单调递增, 所以u(x)>u(0)=0. 为证明推广4,先给出下面的引理 由(*)式,得h′(x)>0,h(x)在[1,+∞)单调递增, 所以h(x)<1. 所以d′(x)<0,d(x)在[1,+∞)单调递减. 所以k′(x)<0. 所以k(x)在[1,+∞)单调递减. 所以x 所以k(x)>1. 下面证明推广4. 证明(ⅰ)当n=1时,由引理得 当n=k+1时,由归纳假设和引理,得 =ln[(k+1)+1]. 所以当n=k+1时,命题成立. 这道高考题的第(3)问与前面两问是并列关系,它们之间没有必然的联系,也就是说前面两问不会做,一点也不影响对第(3)问的证明.有些师生在复习备考中,盲目认为高考很少考查或不会考证明题,进而忽视对数学归纳法的复习,这道高考题对有这样想法的师生敲响了警钟.文章中第(3)问的证明方法3和推广命题4及证明是由我校二年一班学生王鹏博想到的,王鹏博的思路和证明方法使本文更具有趣味性,在此对王鹏博表示衷心的感谢,并祝王鹏博同学在数学方面取得更大的成绩.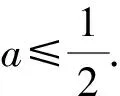


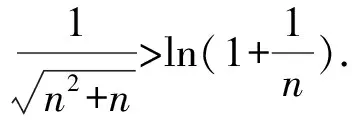


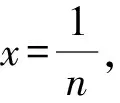


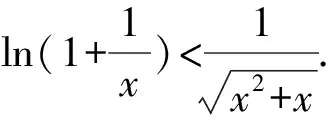
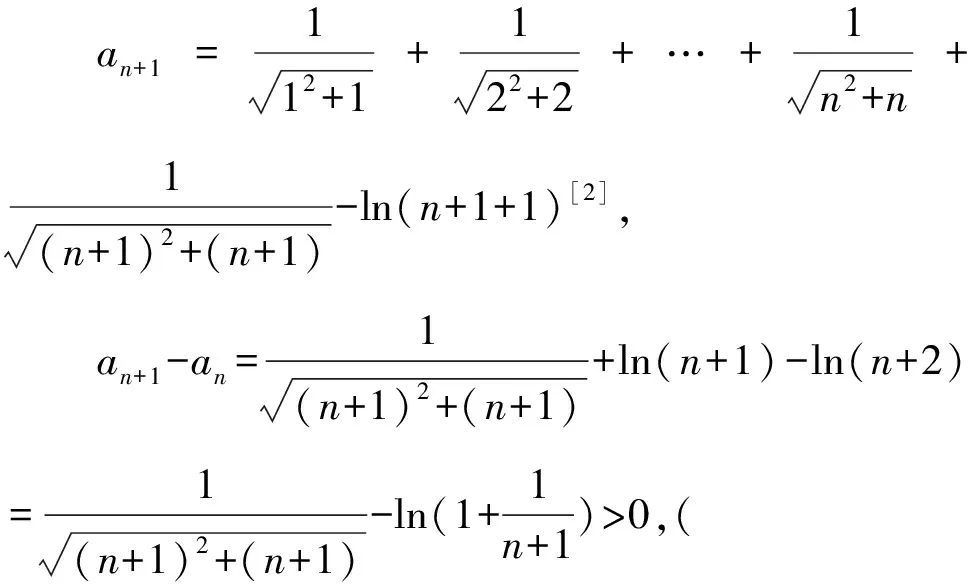
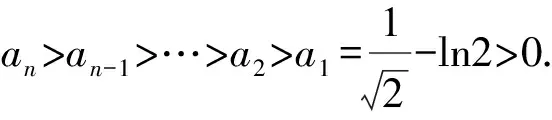
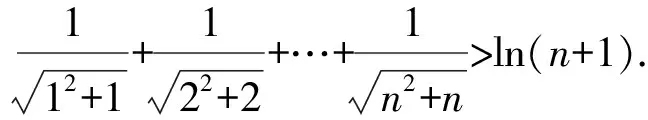



3 命题的推广与推论




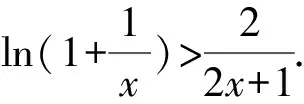


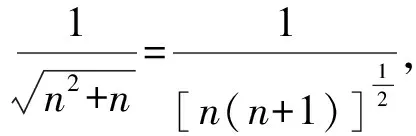
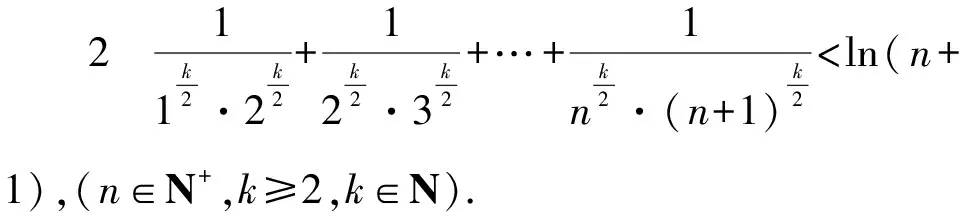



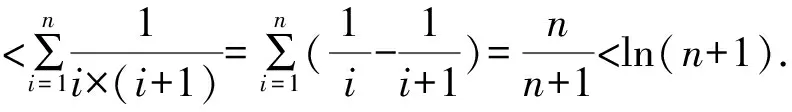

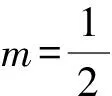

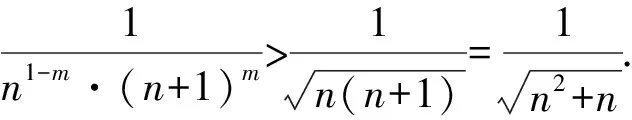
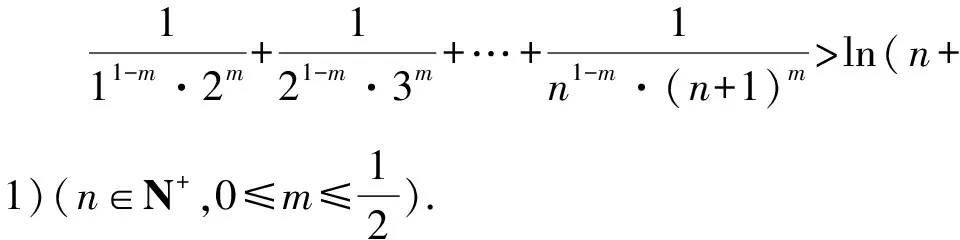
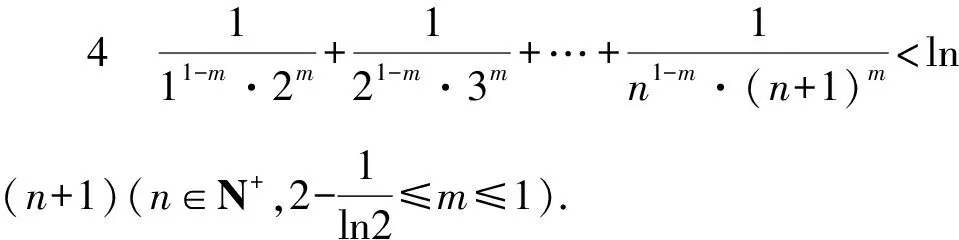


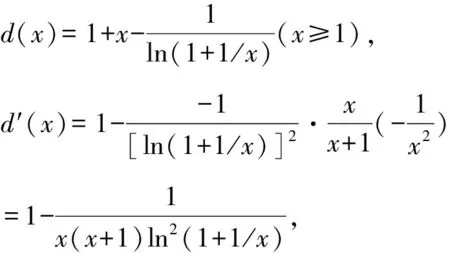
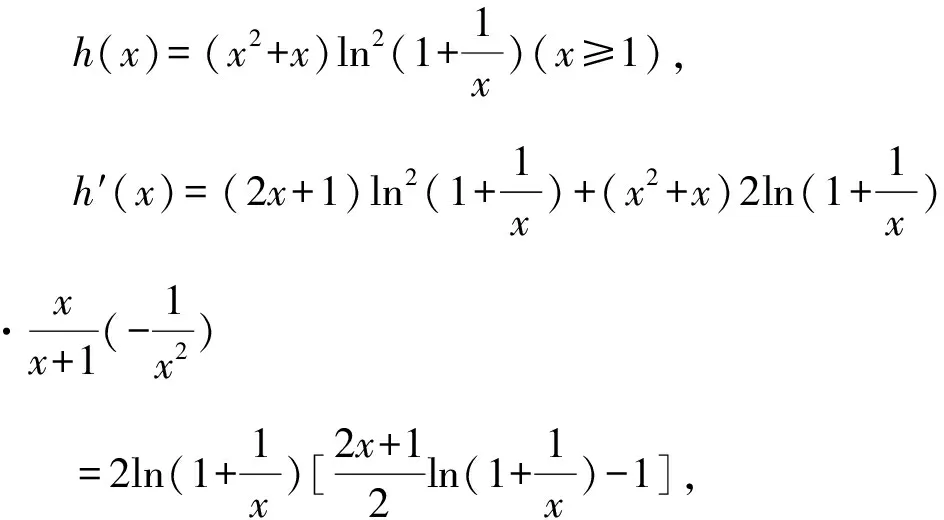

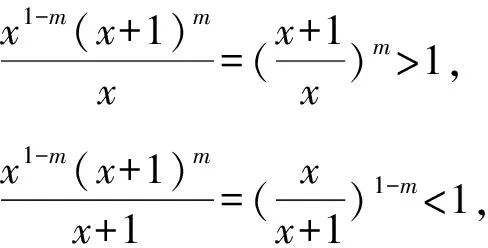
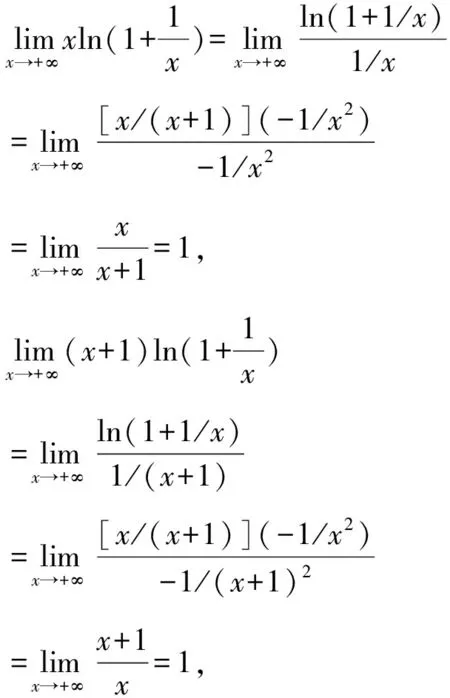
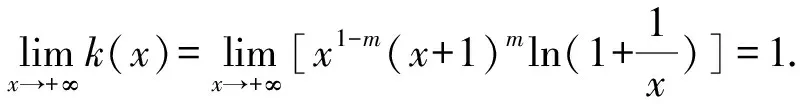
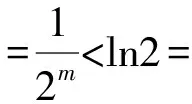
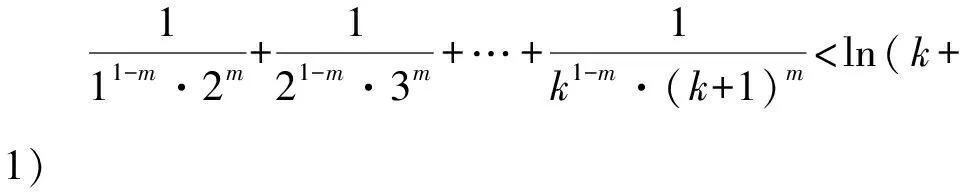
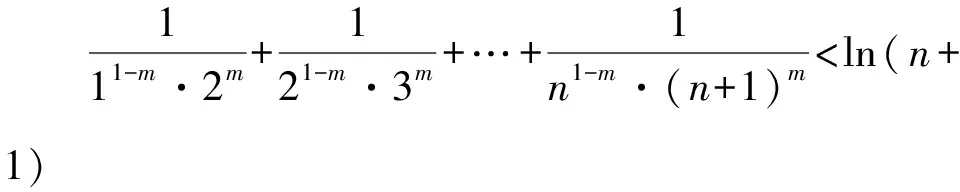
4 结束语

