一道习题的解法探究与反思

谢忠德

(广东省江门市江海区外海中学,广东 江门 529080)

近期,笔者在“直线的方程”这一章节的教学中给学生布置了一道课后习题,当时认为它可能有不少解法,觉得会趣味无穷.于是经过笔者对该题的认真思考和深入研究后,确实得出了多种解法,不足之处,敬请指正.

1 题目呈现

题目已知点P(x,y)在直线2x+y-1=0上,求x2+y2的最小值.

2 解法探究

2.1 利用一元二次函数的性质

解法1 将y=1-2x代入x2+y2,得

x2+y2=x2+(1-2x)2

=5x2-4x+1

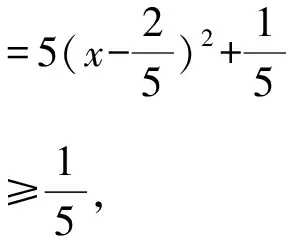
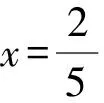
2.2 利用一元二次方程根的判别式

解法2 设x2+y2=a,则将y=1-2x代入,得

a=x2+(1-2x)2.

即5x2-4x+(1-a)=0.

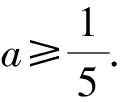
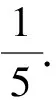
2.3 从导数入手

解法3 将y=1-2x代入x2+y2,得

x2+y2=x2+(1-2x)2

=5x2-4x+1.

设f(x)=5x2-4x+1,求导,得

f′(x)=10x-4.

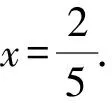
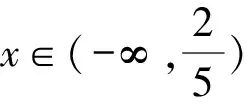
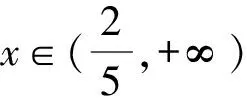
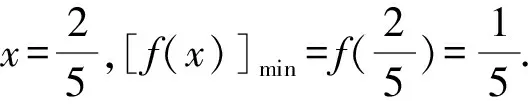
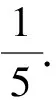
2.4 利用点到直线的距离

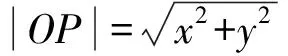
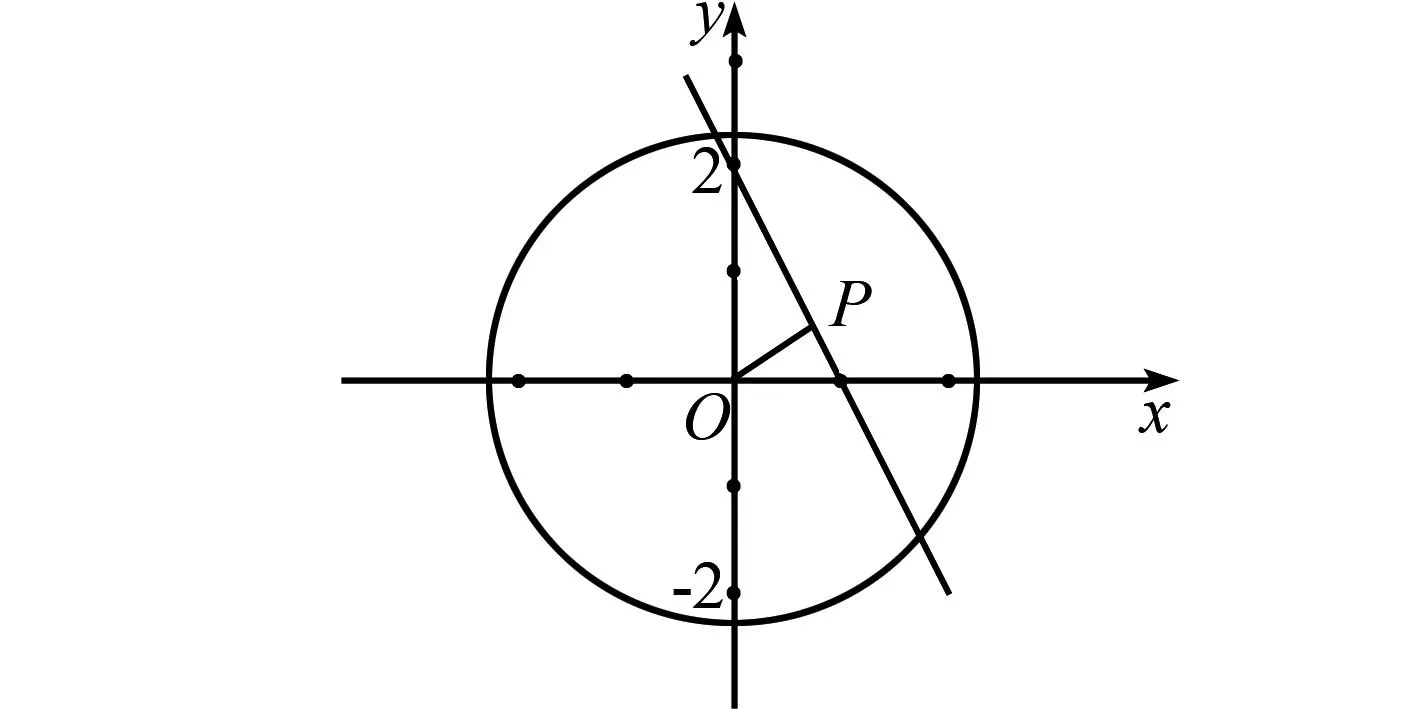
图1 解法4示意图

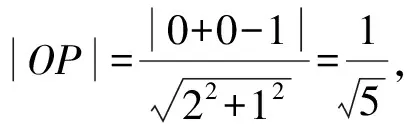
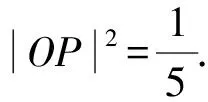
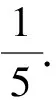
2.5 利用三角换元法

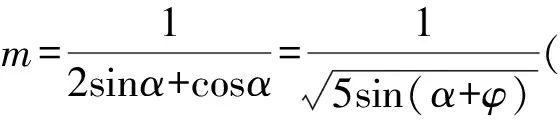
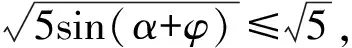
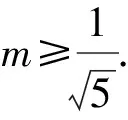
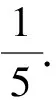
2.6 利用柯西不等式

解法6因为(22+12)(x2+y2)≥(2x+y)2=1,

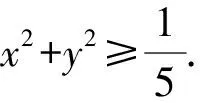
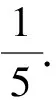
2.7 构造等差数列

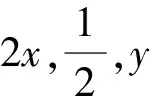
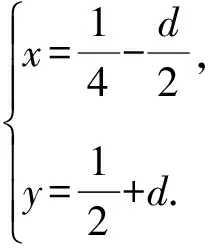
代入x2+y2,得

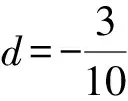
2.8 利用不等式

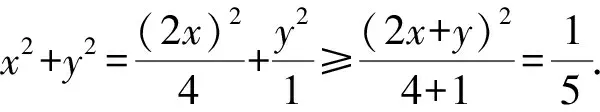
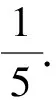
点评利用不等式求最值确实是比较常见的方法,但这里用到的不等式很多人没见过,说明我们的学生在努力学习课本知识以外,需要更多地了解相关知识的延展,因为有很多的知识是需要我们自己去发现和探索的.

2.9 利用平面向量

解法9 设a=(x,y) ,b=(2,1),则由|a||b|≥|a·b|,得

因为2x+y-1=0,

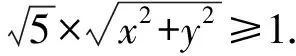
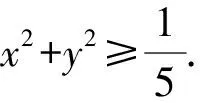
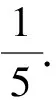
2.10 利用不等式d≤r

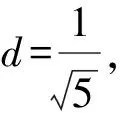
点评利用圆的知识解题不太容易想到,要构造一个圆,利用直线2x+y-1=0与圆x2+y2=m2(m>0)两者之间的联系,才能得到圆心到直线的距离不能超过半径.

2.11 利用极坐标

解法11 显然x≠0,y≠0,不妨设x2+y2=m2(m>0),把x=ρcosθ,y=ρsinθ代入x2+y2=m2(m>0),得ρ2=m2,即ρ=m.

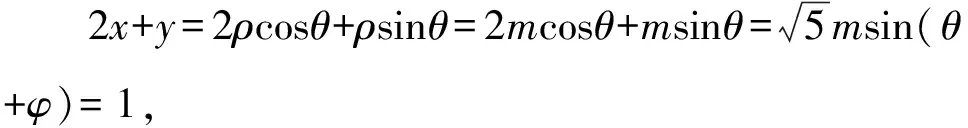
因为-1≤sin(θ+φ)≤1,

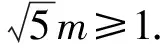
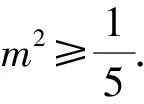
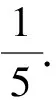
点评其实极坐标法跟解法5的三角换元法非常相似,两者有异曲同工之妙.

2.12 利用方差的性质[1]

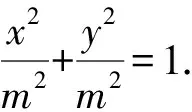
则构造离散型随机变量X的分布列(见表1):

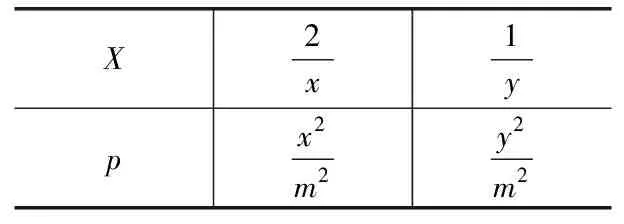
表1 离散型随机变量X的分布列

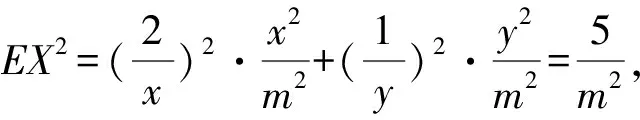
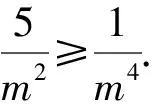
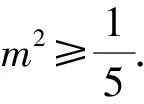
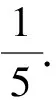
3 结束语

对于这道题的解答,我们从多个角度进行分析,并运用了多种方法.事实上,学生已经有多年的数学学习经历,都打下了较扎实的基础,然而因为某种缘故,在某些方面一直没有得到很好的锻炼,比如观察、联想、迁移、转化.缺乏观察、联想、迁移、转化意识的学生到了高中很难再轻松地学习数学了,总觉得心有余而力不足.我们知道,在课堂上对例题进行分析、讲解是教师教授学生解题的依据,也是学生举一反三的范本,它不仅帮助学生强化和巩固记忆,掌握基础知识,理解基本概念,而且在培养和发展学生思维能力方面也有着重要的作用,同时对形成学生的观察、联想、迁移、转化能力也有很大的促进作用,有助于提高他们的数学解题能力,激发他们对数学的热爱和探索数学的兴趣.