一道2023年北京大学寒假学堂试题的求解与拓广

张志刚

(山东省宁阳县复圣中学,山东 泰安 271400)

圆锥曲线中弦张直角问题历来是高考、竞赛、高校强基计划测试的热点,主要考查曲线方程、定点、面积、最值等相关问题.本文以一道2023年北京大学优秀中学生寒假学堂测试题为例,通过类比和推广,得到圆锥曲线中弦张直角的一般性结论,并通过实例介绍结论的应用.

1 试题呈现

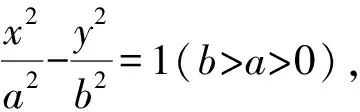
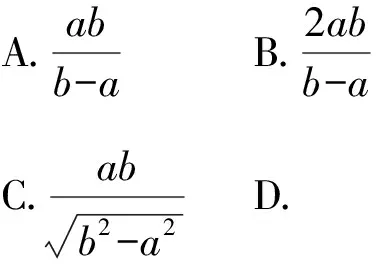
本题是直线与双曲线的位置关系问题,考查直观想象、数学运算、逻辑推理等核心素养,试题设计简洁清新,思维跨度较大,颇具综合性、挑战性和选拔性.

2 试题解答

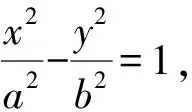
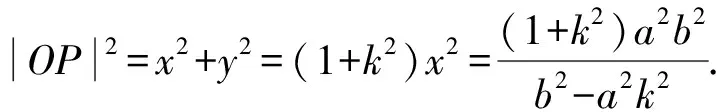
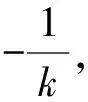
在Rt△OPQ中,设O到直线l的距离为d,则

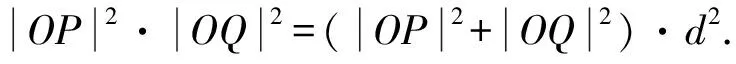
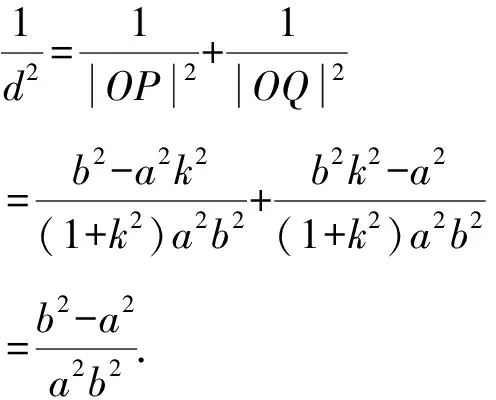
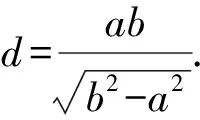
故选C.

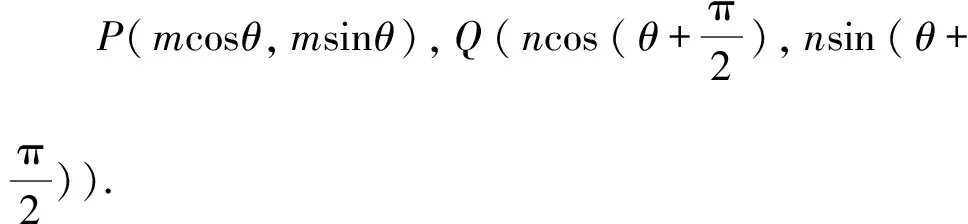
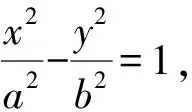
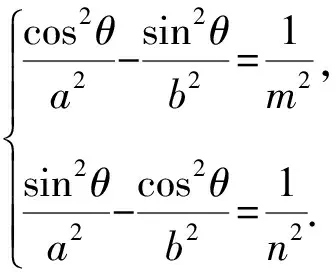
在Rt△OPQ中,设O到直线l的距离为d,则

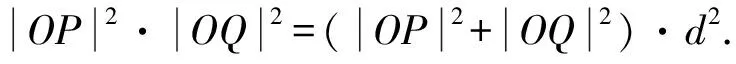
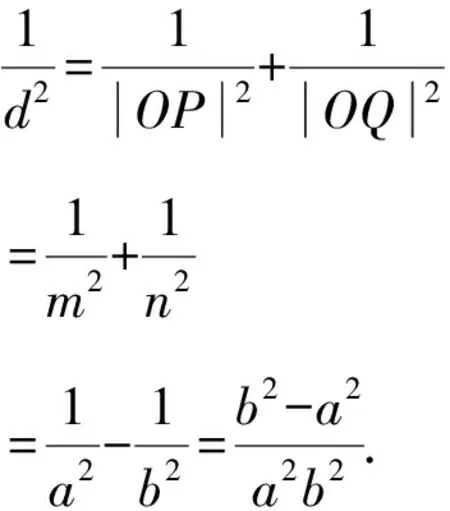
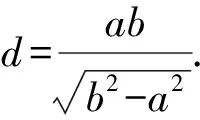
故选C.

3 试题拓广

3.1 张直角弦上高的垂足的轨迹

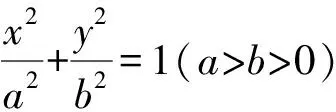
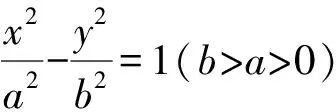
结论3 若直线l与抛物线y2=2px(p>0)交于P,Q两点,且OP⊥OQ,OM⊥PQ,则垂足M的轨迹是圆(x-p)2+y2=p2(x≠0).

下面从原点和定点等特殊点出发,再推广至一般的定点,探讨圆锥曲线的弦张直角的充要条件.

3.2 弦对原点张直角的充要条件

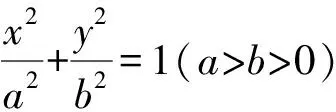
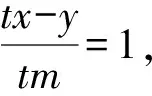
得b2t2(m2-a2)x2+a2(t2m2-b2)y2+2ta2b2xy=0.

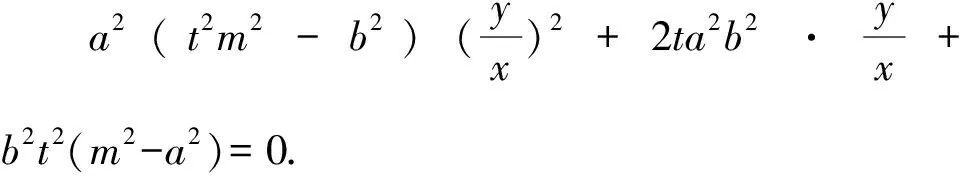
设直线OP,OQ的斜率分别是k1,k2,则k1,k2是方程a2(t2m2-b2)k2+2ta2b2k+b2t2(m2-a2)=0的两个实数根,由根与系数的关系得

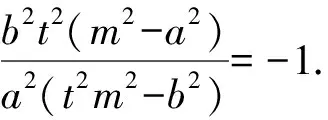
整理,得(a2+b2)t2m2=a2b2(1+t2).

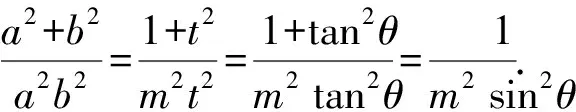
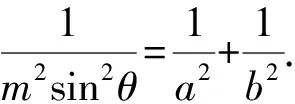
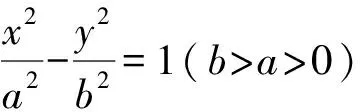
结论5的证明可仿照结论4完成,不再赘述.

将以上结论一般化,即得结论6.

结论6 若直线l:mx+ny=1与有心二次曲线Ax2+By2=1(AB≠0)交于P,Q两点,O为原点,则OP⊥OQ的充要条件是A+B=m2+n2.

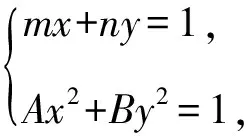
Ax2+By2=(mx+ny)2.

即(B-n2)y2-2mnxy+(A-m2)x2=0.

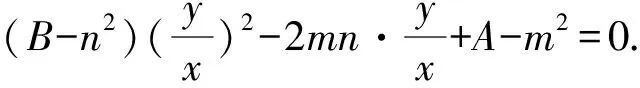
设直线OP,OQ的斜率分别是k1,k2,则k1,k2是方程(B-n2)k2-2mnk+A-m2=0的两个实数根,由根与系数的关系得

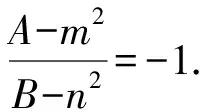
即A+B=m2+n2.

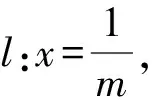
设P(x1,y1),Q(x2,y2),由根与系数的关系,得

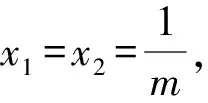
所以x1x2+y1y2=0.

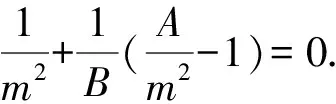
整理,得A+B=m2+n2.

综上,OP⊥OQ的充要条件是A+B=m2+n2.

3.3 弦对顶点张直角的充要条件

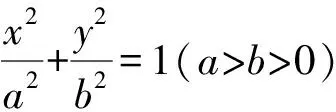
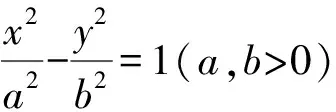
结论9 若直线l与抛物线y2=2px(p>0)交于P,Q两点,A为抛物线的顶点,则AP⊥AQ的充要条件是直线l过点(2p,0).

结论7、8的证明可参考文献[1],下面给出结论9的证明.

证明设直线l:mx+ny=1,代入y2=2px,得

y2=2px(mx+ny),

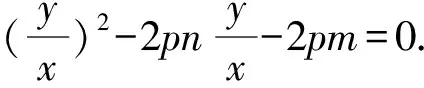
设直线OP,OQ的斜率分别是k1,k2,则k1,k2是方程k2-2pnk-2pm=0的两个实数根,由根与系数的关系得k1k2=-2pm.

又OP⊥OQ,所以-2pm=-1,即2pm=1.

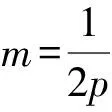
-2pny=x-2p.

故直线l过点(2p,0).

把结论7、8中的右顶点改为其他顶点,把结论9中开口向右改为其他开口方向,也有类似结论,请读者自证.

3.4 弦对定点张直角的充要条件

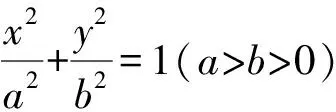
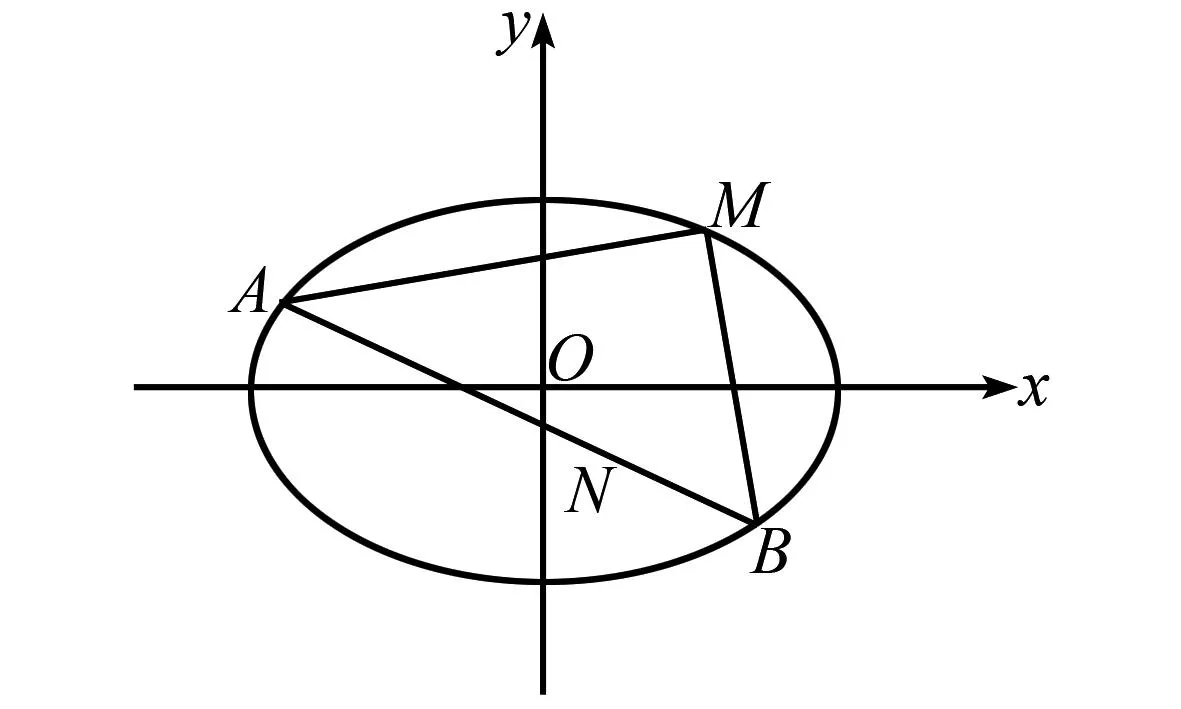
图1 结论10示意图

证明设P(x1,y1),Q(x2,y2),

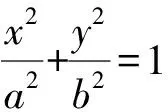
(a2+b2k2)y2+2b2mky+b2m2-a2b2=0.

由根与系数的关系,得

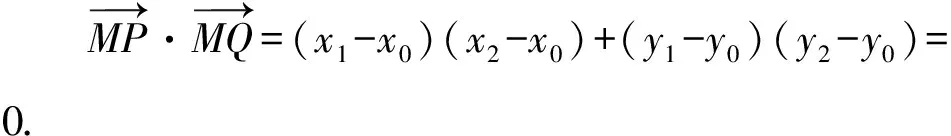
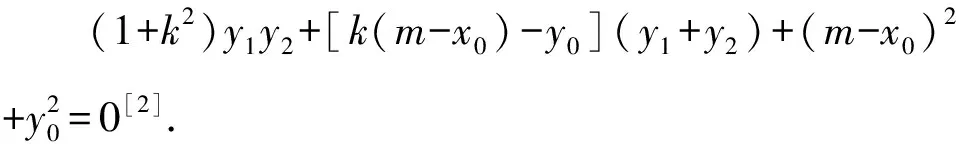
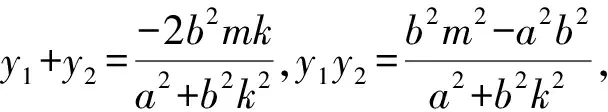
代入上式并整理,得

解得m=x0-ky0(舍去)或

故直线l的方程为

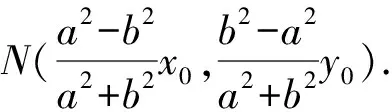
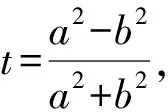
则直线l的方程为y=nx-t(nx0+y0).

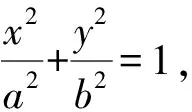
由根与系数的关系,得

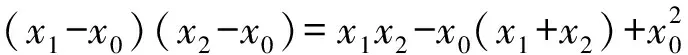
又y1=nx1-t(nx0+y0),

y2=nx2-t(nx0+y0),

所以y1+y2=n(x1+x2)-2t(nx0+y0),

y1y2=[nx1-t(nx0+y0)][nx2-t(nx0+y0)]

=n2x1x2-nt(nx0+y0)(x1+x2)+t2(nx0+y0)2

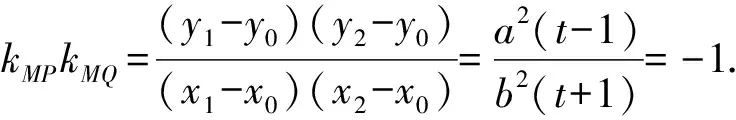
故MP⊥MQ.

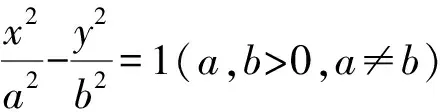
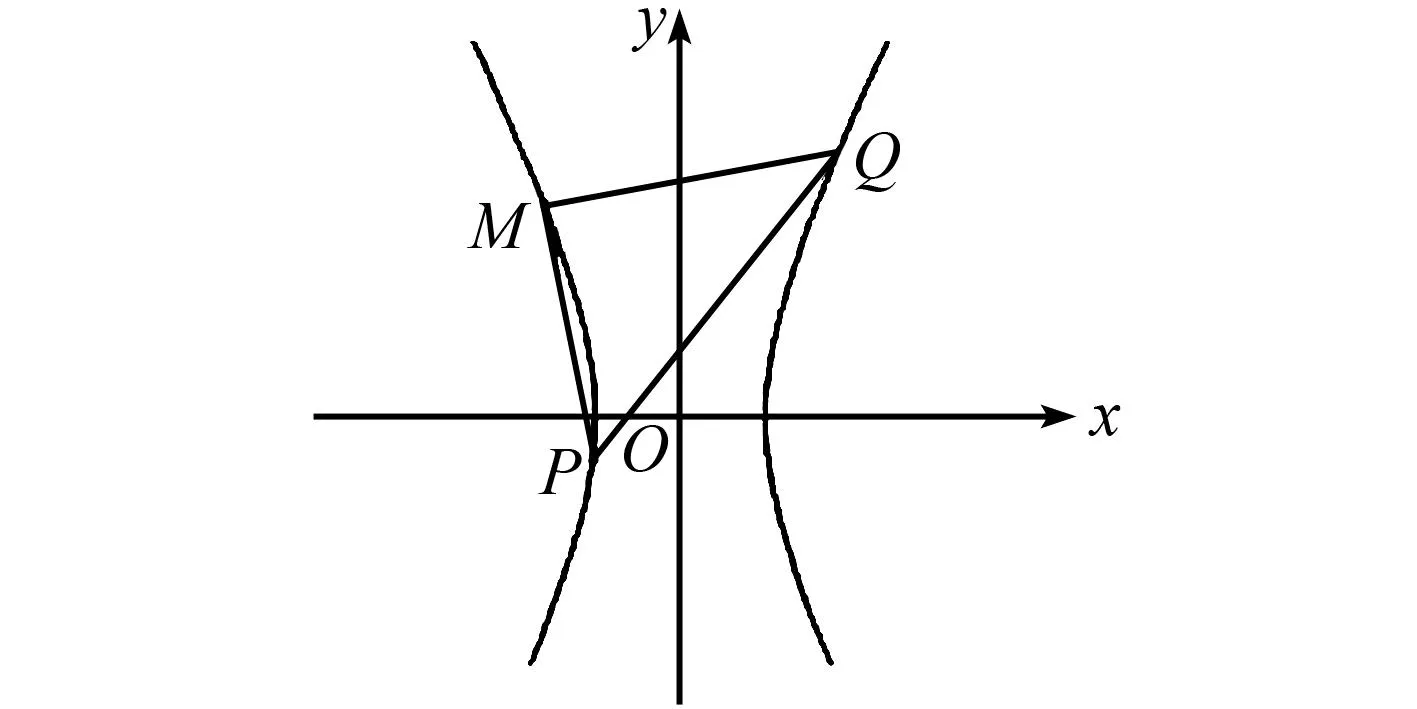
图2 结论11示意图

结论12 如图3,若直线l与抛物线y2=2px(p>0)交于P,Q两点,点M(x0,y0)为抛物线上异于P,Q两点的一个定点,则MP⊥MQ的充要条件是l过定点N(2p+x0,-y0).

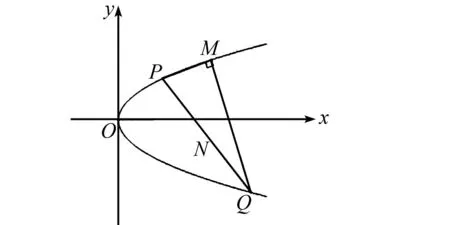
图3 结论12示意图

4 结论的应用

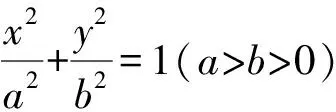
解析由结论1知,垂足M的轨迹是圆

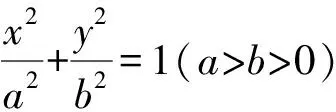
(1)求椭圆的方程及离心率;

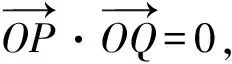
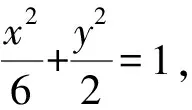
(2)由(1)得A(3,0).

设直线PQ的倾斜角为θ,由结论4得

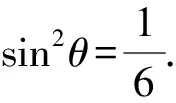
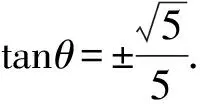
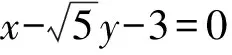
例3 (2007年高考山东卷理科第21题)已知椭圆C的中心在坐标原点、焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1.

(1)求椭圆C的标准方程;

(2)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.证明:直线l过定点,并求出该定点的坐标.

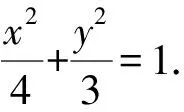
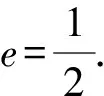
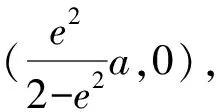
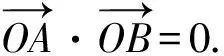
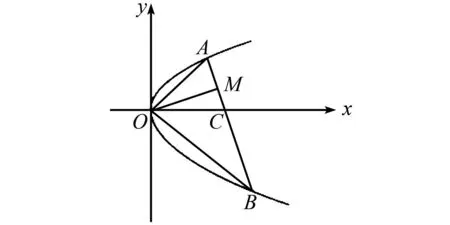
图4

(x-2)2+y2=4(x≠0).

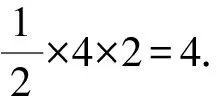
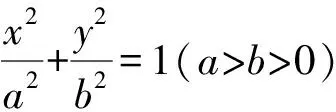
解析由结论1知,

由基本不等式,得

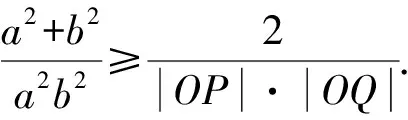
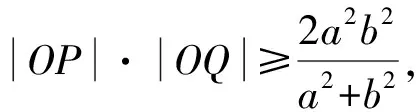
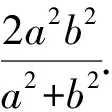
5 结束语

高考题实际上是将必然有的一些结论特殊化,化一般为特殊,让学生用所学知识来解决必然成立的问题,只有学生把方法、知识、技巧融为一体,做题时旁征博引,融会贯通,以不变应万变,解一题而晓一类题,这样势必会得出一系列理想的结论.