解析几道以迭代数列为背景的高考题
薛红利
(长春第六中学,吉林 长春 130000)
高考题一般都是大学老师命制的,所以高考题尤其是高考压轴题,有高等数学背景也是常有的事.这就要求一线教师不仅要会做高考压轴题,还要弄清楚高考压轴题的高数背景,这样才能看清试题的命制思路和背景,才能更好地服务于教学.
1 预备知识
定义称xn+1=f(xn),n=1,2,…为迭代数列,称其中的f(x)为迭代函数.(以下均假设f与n无关)[1].
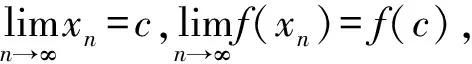
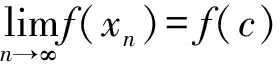
定理2设函数f(x)在区间I上单调,数列{xn}满足迭代公式xn+1=f(xn),n∈N*,且xn∈I,n∈N*,则只有两种可能:
(1)当f(x)为单调递增时,{xn}为单调数列;
(2)当f(x)为单调递减时,{xn}的子列{x2n-1}和{x2n}是具有相反单调性的两个单调子列.
其几何解释如下图:
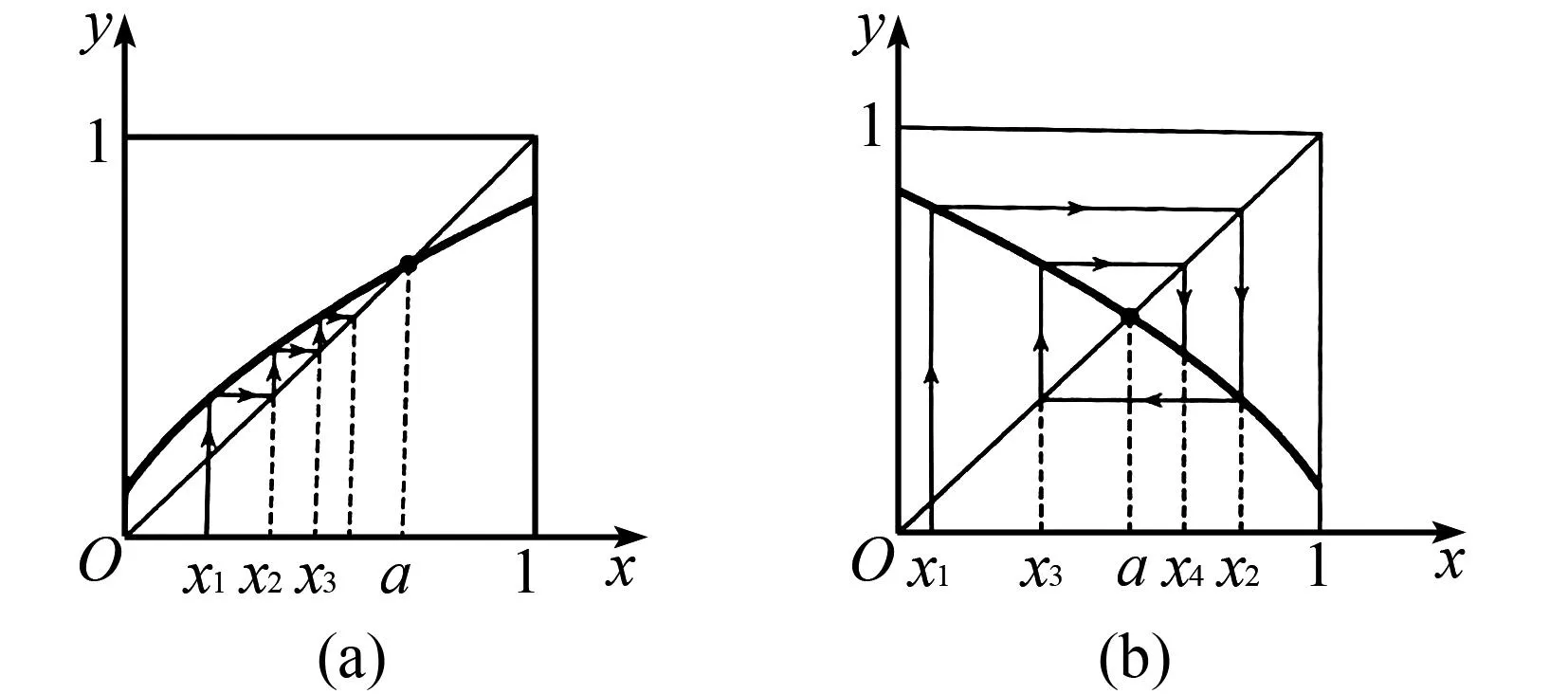
图1 定理2几何解释
2 高考试题及其背景分析
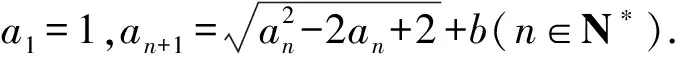
(1)若b=1,求a2,a3及数列{an}的通项公式;
(2)若b=-1,问:是否存在实数c使得a2n an+1=f(an). 下面用数学归纳法加强命题:a2n 所以a2 假设当n=k(k≥1)时命题成立,即 a2k 因为f(x)在(-∞,1]上单调递减,所以c=f(c)>f(a2k+1)>f(1)=a2.所以1>c>a2k+2>a2.所以c=f(c) 本题以迭代数列为背景,考查迭代数列的极限.由定理1,先求出f(x)的不动点,即令c=f(c),再证明a2n 同理可得,a3=f(a2)>f(a4)=a5. 一直下去,可得: a1>a3>…>a2n-1>a2n+1(n∈N*), a2 对以上两式两边取极限,可得 解法2当b=-1时由题意,得 (an+1+1)2=(an-1)2+1. 从而得到(a2n+1+1)2=(a2n-1)2+1. ① 假设存在实数c使得a2n (a2n+1)2<(c+1)2<(a2n+1+1)2. 由①式得(a2n+1)2<(c+1)2<(a2n-1)2+1. 例2(2012年大纲全国卷理)函数f(x)=x2-2x-3.定义数列{xn}如下:x1=2,xn+1是过两点P(4,5),Qn(xn,f(xn))的直线PQn与x轴的交点的横坐标. (1)证明:2≤xn (2)求数列{xn}的通项公式. (1)参考答案用的是数学归纳法. 所以2≤xn (2)若b=1,问:是否存在实数c使得a2n (2)方法类似于例1的解法2. 根据以上分析,其高数背景是定理2的情形(2),即需证子列{a2n}和{a2n-1}分别单调,且收敛于同一极限c. 即0 由f(x)在(0,1]上单调递减,得a2=f(a1) a2 a1>a3>a5>…>a2n-1>a2n+1. 站得高,才能看得远.作为教师,应该具备一定的高等数学知识,这其实就是我们大学本科四年学习的基本功,这样,遇到压轴题才能轻松应对,游刃有余.在具体操作上,可先分析出试题的高数背景,获得答案,这时就得到了解题的方向,然后再用高中知识和方法去书写解题过程.由此可见,掌握一定的高数知识,弄清楚高考题的高数背景和命制思路是非常必要的.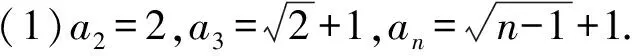
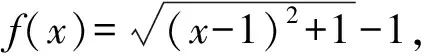
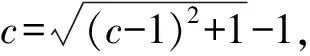
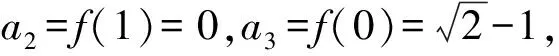
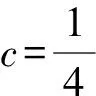
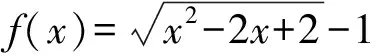
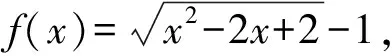
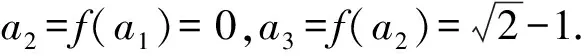
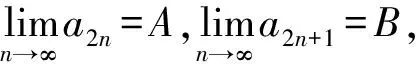
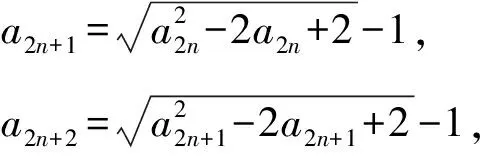
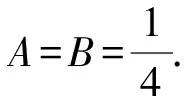
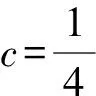
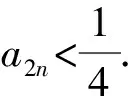
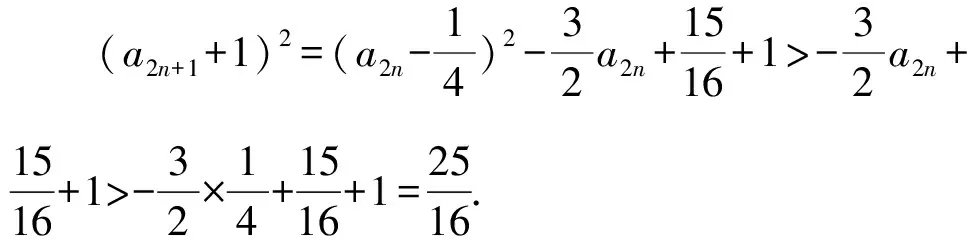
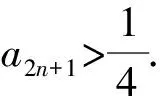
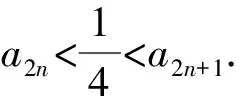
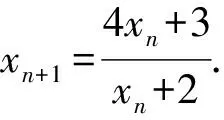
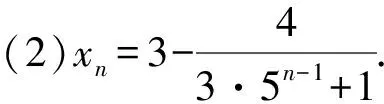
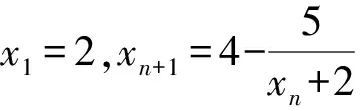
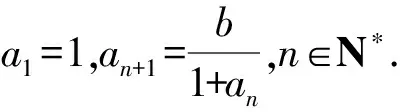

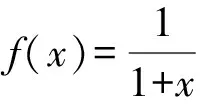
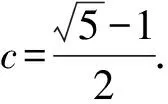
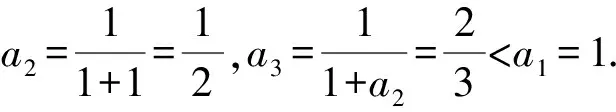
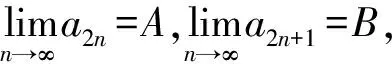
3 结束语

