巧借导函数解决高中数学不等式压轴难题
李 强
(苏州大学实验学校高中部,江苏 苏州 215131)
不等式问题是高中数学的必考知识点,同时也是重难点.高中数学不等式的压轴难题主要出现在解答题最后一题的第二小问中,与函数、数列等知识点联系较为紧密,考查形式多为不等式的证明或恒成立问题,难度较大.在求解时,我们可以根据已知条件,结合函数与方程思想,巧借导函数解决高中数学不等式压轴难题.
1 利用导函数解决不等式证明问题
在利用导函数解决不等式证明问题时,需要结合构造法.根据所要证明的不等式,构造与之相关的函数,再利用函数的单调性、极值和最值加以证明[1].高中阶段,常见的构造方法包括:
(1)直接构造法.将需要证明的不等式f(x)>g(x)转化为证明f(x)-g(x)>0或f(x)-g(x)<0,进而通过构造辅助函数F(x)=f(x)-g(x)并证明函数F(x)与0的关系进而证明原不等式;
(2)适当放缩构造函数.根据已知条件适当放缩,或利用常见的放缩结论,如
lnx≤x-1,
ex≥x+1,
lnx
(3)构造形似函数.即将原不等式进行适当变形,如移项、通分、取对数,从而将不等式转化为左、右两边为相同结构的式子的形式,再根据“相同形式”构造辅助函数,利用函数的性质求解[2];
(4)构造双函数.若直接构造函数求导难以判断函数的单调性和零点,那么我们可以分开构造双函数f(x)和g(x),通过比较证明.
例1 (成都高三9月月考)已知函数f(x)=xlnx-2ax2+x,a∈R.
(1)若f(x)在(0,+∞)内单调递减,求a的取值范围;
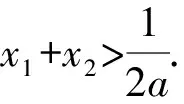
解析(1)由题可得
f′(x)=lnx+2-4ax,x>0,
因为f(x)在(0,+∞)内单调递减,
所以f′(x)=lnx+2-4ax在(0,+∞)内恒成立.
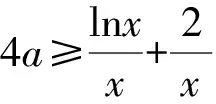
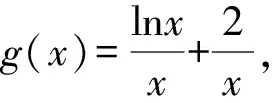

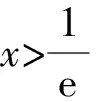
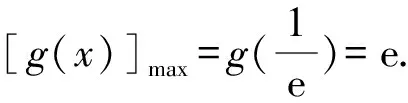

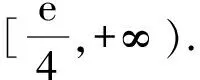
(2)若函数f(x)有两个极值点为x1和x2,则f′(x)=lnx+2-4ax在(0,+∞)内有两根x1和x2.
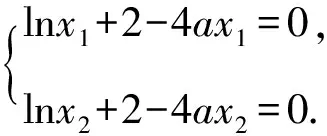
两式相减,得
lnx1-lnx2=4a(x1-x2).
设0 所以h(t)在t∈(0,1)上单调递减. 所以h(t)>h(1)=0. 题后反思本题主要考查函数与不等式的综合问题.在求解时需要利用构造法将不等式问题与函数结合起来,再结合导函数的性质,判断函数与零点的关系进而证明.构造函数展开讨论是解决本题的关键和突破点,思路要重点把握. 在利用导函数解决不等式的恒成立问题时,有两种常见思路:一种是先利用综合法,结合导函数的零点之间的大小关系的决定条件,确定分类讨论的标准.分类后,判断不同区间函数的单调性得到最值,进而证明不等式[3].另一种,则是直接通过导函数,确定其与零点之间的关系,并以此划分分类标准证明不等式恒成立.通常,若a>f(x)对x∈D恒成立,则只需要a>[f(x)]max;若a 例2(杭州高三一模)已知函数f(x)=(x-a)ex(a∈R). (1)讨论f(x)的单调性; 解析(1)因为f′(x)=(x-a+1)ex, 当x∈(-∞,a-1)时,f′(x)<0; 当x∈(a-1,+∞)时,f′(x)>0; 故f(x)的单调递减区间为(-∞,a-1),单调递增区间为(a-1,+∞). (2)由g(x)=f(x)+lnx-x-b,b∈Z, 以此构造函数令h(x)=(x-2)ex+lnx-x,则 即x0=-lnx0. 所以[h(x)]max=h(x0) =(x0-2)ex0+lnx0-x0 因为b∈Z,即b的最小值为-3. 题后反思本题主要考查的是不等式的恒成立以及函数的单调性问题.第一小问比较简单,直接对f(x)求导,根据导函数与函数单调性之间的关系即可顺利求解.第二小问中涉及了不等式的恒成立问题,求解时,首先需要将不等式进行变形,构造函数,进而对新函数进行求导,并判断出在已知区间内函数的单调性情况,找出极值,综合求解.本题主要考查同学们的推理能力和计算能力,属于高中数学压轴题中的中等难度题,思路和方法要重点掌握. 虽然不等式问题在高中数学压轴题中较为常见,但在求解时也是有具体的方法和思路可循的.在解决高中数学的不等式压轴难题时,我们需要利用函数与方程思想,将原不等式进行适当变形或直接利用构造法将不等式问题转化为函数问题.再利用导函数与函数单调性、极值之间的关系综合求解.当然,高中阶段不等式压轴问题中还常涉及含参变量问题、求取值范围问题,同学们都需要在日常的学习和训练过程中,及时对不等式压轴问题进行归纳和总结,保证自己在考场上能做到游刃有余.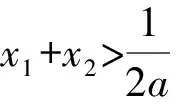
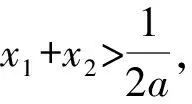
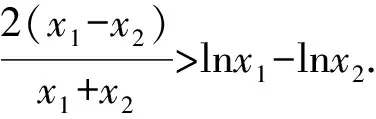

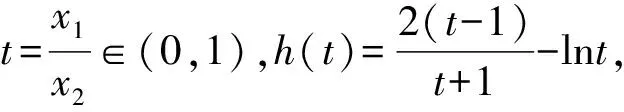

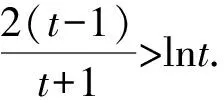
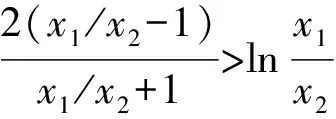
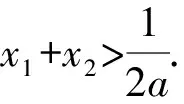
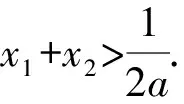
2 利用导函数解决不等式恒成立问题
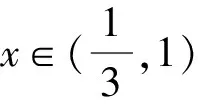
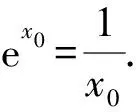
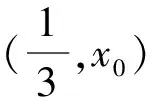
3 结束语

