一道双曲线联考题的解法与结论推广

李 寒

(贵州省贵阳市第一中学,贵州 贵阳 550081)

双曲线是一种重要的圆锥曲线,是高考命题的重点内容,尤其是近年高考或各地模拟考试中,双曲线内容常出现在解答题中进行考查,体现了高考命题者对双曲线内容的青睐.下面对一道高三双曲线联考题的解法和结论进行探究.

1 考题再现

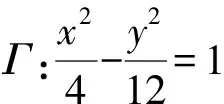
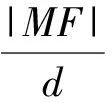
(2)若M(-4,6)为曲线Γ上一点,直线MA,MB分别与直线l1交于D,E两点,问以线段DE为直径的圆是否过定点?若是,求出定点坐标;若不是,请说明理由.

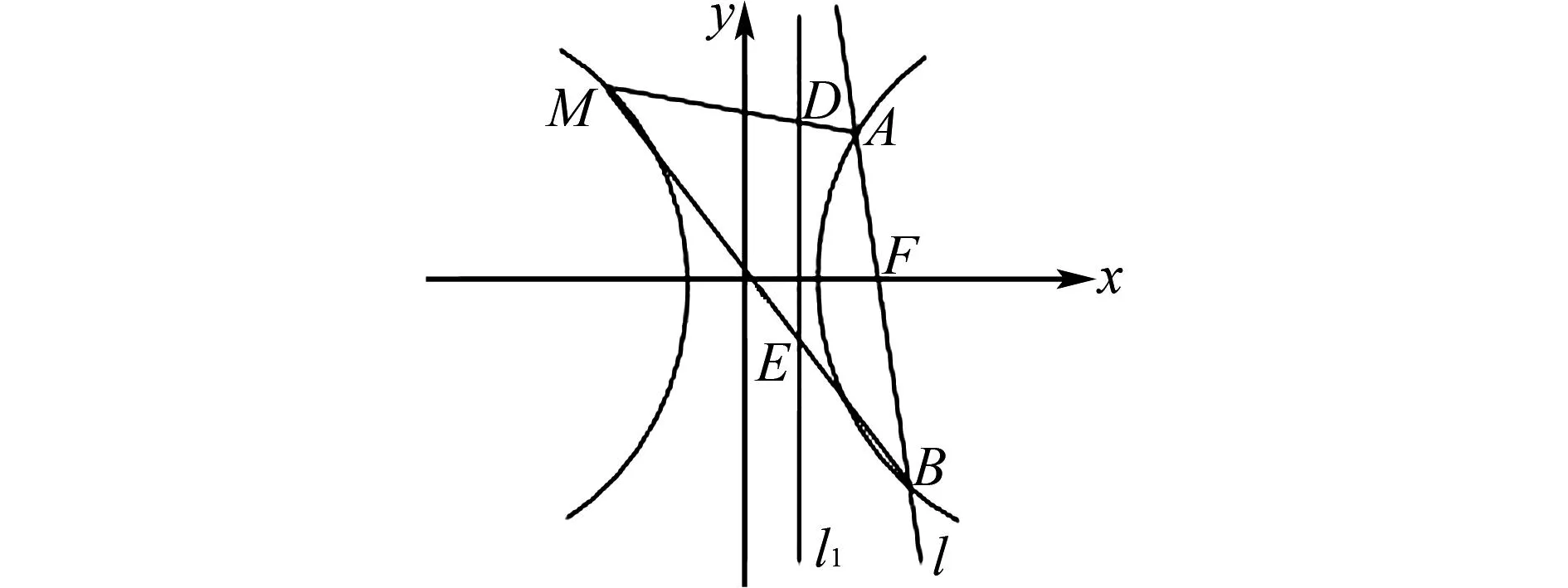
图1 2023年2月浙江省七彩联盟返校联考数学21题图

2 解法探究

2.1 第(1)小题解析

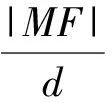
解析根据题意,易得F(4,0).

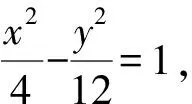
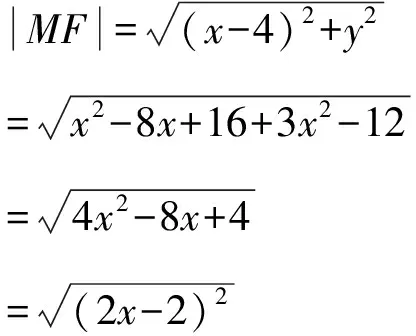
=2|x-1|,

d=|x-1|,

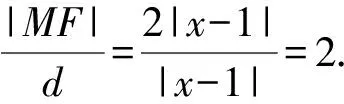
点评由于点F是双曲线Γ的右焦点,直线l1是双曲线Γ的右准线,所以该小题实质上考查的是双曲线的第二定义.

2.2 第(2)小题解析

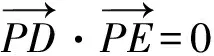
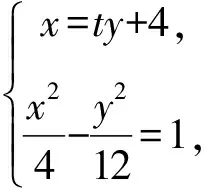
(3t2-1)y2+24ty+36=0.

设A(x1,y1),B(x2,y2),所以

直线MA的方程为

令x=1,得

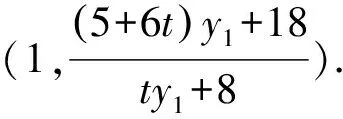
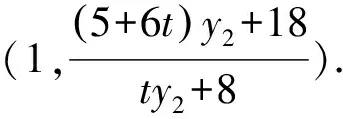
由图形的对称性可知,定点必在x轴上,设定点P(m,0),则

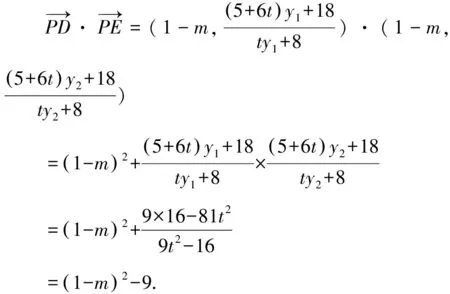
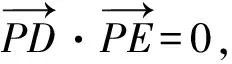
故以线段DE为直径的圆过定点P(-2,0)或P(4,0).

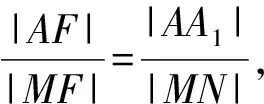
解法2 如图2,过点A作AA1⊥直线l1,垂足为点A1,过点B作BB1⊥直线l1,垂足为点B1,过点M作MN⊥直线l1,垂足为点N,连接FE,FD.

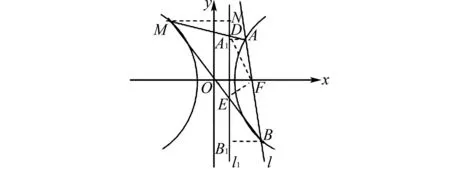
图2 解法2示意图

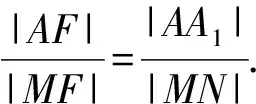
又由△AA1D∽△MND,得

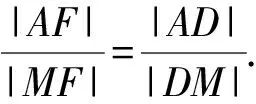
所以在△AFM中,FD是∠AFM的角平分线.

所以∠AFD=∠DFM.

同理在△BFM中,FE是∠BFM的角平分线.

所以∠BFE=∠MFE.

所以∠EFD=∠DFM+∠MFE

所以FD⊥FE.

故以线段DE为直径的圆过定点F(4,0),根据对称性可知也过定点(-2,0).

点评该小题考查的是圆过定点问题.解法1首先引入参变量t,设出直线l的方程,通过联立方程组求出两交点纵坐标的和与积,然后利用直径所对的角是直角,构造向量,运用向量数量积为0建立等式关系,求出定点.其中由图形的对称性猜测定点位置,从而明确方向,进而简化计算.解法1是解决这类问题的通性通法.解法2根据题意条件,通过作出辅助线,挖掘并利用隐含的三角形相似、三角形内角平分线性质得到线段的垂直关系,从而找到圆过的定点,其解题过程十分简捷、巧妙,体现了平面几何知识在简化解析几何计算中的优越性.但解法2逻辑推理要求高,思维难度大,不易切入.

3 推广探究

我们在这里将目光放到对第(2)问的推广探究上.

3.1 延伸推广

从对上述联考题的条件和结论的分析可以看出,F是双曲线Γ的右焦点,直线l1则是双曲线Γ的右准线,M是双曲线Γ左支上的一点,其结论是以线段DE为直径的圆过的定点是焦点F和焦点F关于线段DE的对称点.由此,我们来思考下面的两个问题:

(1)能否把联考题的结论延伸为一般双曲线的情形?

(2)若F是双曲线Γ的左焦点,直线l1则是双曲线Γ的左准线,M是双曲线Γ右支上的一点,是否可以得到同样的结论?

答案是肯定的!于是由联考题推广为一般情形下双曲线的两个结论:

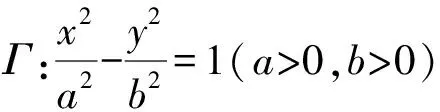
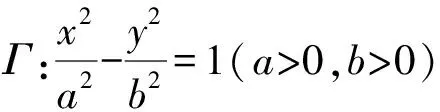
结论1和结论2的证明可按联考题第(2)问的证法2的过程进行,这里从略.

3.2 类比推广

圆锥曲线有许多相似的性质或结论,由于双曲线与椭圆均为有心二次曲线,能否将双曲线的结论1和结论2分别类比到椭圆,得到同样的结论?答案也是肯定的,于是有:

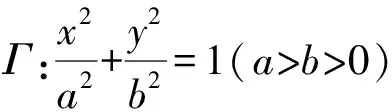
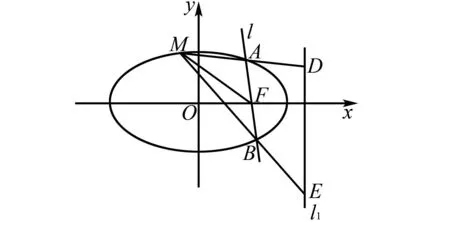
图3 结论3示意图

证明如图4,过点A作AA1⊥直线l1,垂足为点A1,过点B作BB1⊥直线l1,垂足为点B1,过点M作MN⊥直线l1,垂足为点N,连接FE,FD.

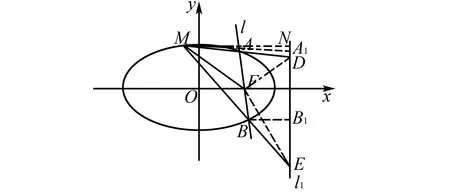
图4 结论3证明图

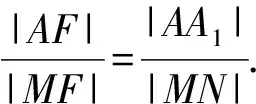
又由△AA1D∽△MND,得

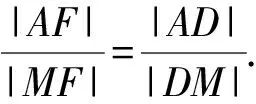
所以FD是△AFM的∠AFM的外角平分线.

所以∠AFD=∠DFM.

同理,FE是△BFM的∠BFM的外角平分线.

所以∠BFE=∠MFE.

所以∠EFD=∠DFM+∠MFE

所以FD⊥FE.

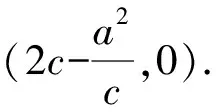
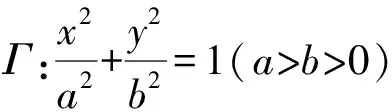
结论4的证明可按结论3的证明过程进行,这里从略.

4 结束语

对典型试题的解法与结论推广进行探究,就是指对问题从不同视角来审视,以不同的切入点探究问题,其实质是对试题的“二次开发”.通过对试题的剖析和思考,展开问题的来龙去脉和知识间的纵横联系,站在一定的高度去思考问题,突出数学本质,使知识达到融会贯通,使思维得到升华,进而优化数学思维品质[1].