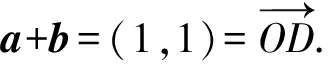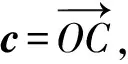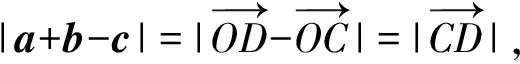2023年全国数学联赛(贵州赛区)预赛试题及其解析

李鸿昌

(北京师范大学贵阳附属中学,贵州 贵阳 550081)

2023年全国数学联赛(贵州赛区)预赛试题于2023年6月17日已落下帷幕,第1题至第9题,稍微比全国联赛一试试题简单一点,第10题和第11题属于全国联赛二试内容,但难度稍小.试题原创度极高,且有很好的区分度,具有极好的选拔功能.

一、填空题：本大题共8小题,每小题8分,满分64分.

1.设集合A={(x,y)|x+y=1},B={(x,y)|x2+y2=2},C=A∩B,则集合C的子集的个数是____.

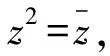
3.已知a,b是单位向量,|3a+4b|=|4a-3b|,若|c|=2,则|a+b-c|的最大值是____.

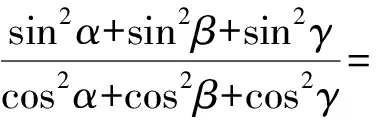
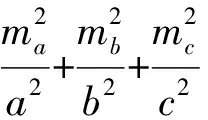
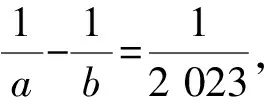
7.已知函数f(x)=x3-2x2-3x+4,若f(a)=f(b)=f(c),其中a

8.已知5名同学分别擅长的学科为语文、数学、物理、化学、历史.现有5份试卷(语文、数学、物理、化学、历史各一份),老师随机分发给每名同学一份试卷,则至少有4名同学得到的试卷与自己擅长的学科不符的概率是____.

二、解答题：本大题共3小题,满分56分. 解答应写出文字说明、证明过程或演算步骤.

9.(本题满分16分)设{an}是正项等差数列,公差为d(d>0),前n项和为Sn,m,n,p,q均为正整数.若n

(1)aman

(2)Sm+Sn>Sp+Sq.

10.(本题满分20分)如图1,设P是四边形ABCD内一点,满足∠BPC=2∠BAC,∠PCA=∠PAD,∠PDA=∠PAC.

求证:∠PBD=|∠BCA-∠PCA|.

图1 四边形

11.(本题满分20分)定义:若一个数列中的每一项都是完全平方数,则称这种数列为完方数列.已知数列{xn}满足x0=0,x1=3,xn+1+xn-1=4xn,证明:{xn-1·xn+1+9}是一个完方数列.

参考

1.易知集合C有2个元素,故C的子集有22=4个.

3.因为|a|=|b|=1,|3a+4b|=|4a-3b|,两边平方得a·b=0,即a⊥b.

不妨设a=(1,0),b=(0,1),D(1,1),则

4.由于三条侧棱两两垂直,易知

由面积射影定理得

从而sin2α+sin2β+sin2γ=2.

5.由中线长公式,知

由基本不等式,可得

即2 023b-2 023a-ab=0.

从而(2 023-a)(2 023+b)=2 0232.

又2 023-a<2 023+b,且2 023=7×17×17,

所以2 0232=12×2 0232=72×172×172.

因此2 023-a=12,7,17,72,7×17,172,72×17;2 023+b=2 0232,7×174,72×173,174,7×173,72×172,173.

故所有正整数对(a,b)的个数为7.

7.设f(a)=f(b)=f(c)=m,g(x)=f(x)-m,则a,b,c是函数g(x)的三个零点,即a,b,c是方程x3-2x2-3x+4-m=0的三个根.

由根与系数的关系知,

a+b+c=2,ab+bc+ca=-3.

故a2+b2+c2=(a+b+c)2-2(ab+bc+ca)=22-2×(-3)=10.

9.(1)先证mn

因为n

所以mn-pq=mn-p(m+n-p)=mn-pm-pn+p2=(m-p)(n-p)<0.

即mn

因为m+n=p+q,mn

(2)先证mam+nan>pap+qaq.

mam+nan-pap-qaq=m[a1+(m-1)d]+n[a1+(n-1)d]-p[a1+(p-1)d]-q[a1+(q-1)d]=(m+n-p-q)a1+[m(m-1)+n(n-1)-p(p-1)-q(q-1)]d=(m2-m+n2-n-p2+p-q2+q)d=[(m2-p2)-(m-p)-(q2-n2)+(q-n)]d=[(m-p)(m+p-1)-(q-n)(q+n-1)]d=λ(m+n+p+q-2)d.

其中λ=m-p=q-n>0,又d>0,且m+n+p+q-2>0,故mam+nan>pap+qaq.

图2 四边形

10.如图2所示,设AB的中垂线与AC交于点E,由∠BEC=2∠BAC=∠BPC知B,E,P,C共圆.

如图3所示,设直线EP与△APD外接圆的另一个交点为F.由∠PAC=∠PDA知,AC与△APD的外接圆相切,所以EB2=EA2=EP·EF.

于是∠EFB=∠EBP=∠ECP=∠PAD=∠PFD,故B,D,F三点共线.这样,∠PCA=∠PBE=∠PFB=∠BPE-∠PBD=∠BCA-∠PBD,即∠PBD=∠BCA-∠PCA.

综上,命题得证.

11.由xn+1+xn-1=4xn以及x0=0,x1=3可求得

又因为xn+1=4xn-xn-1且x0=0,x1=3都为整数,所以可知xn必为整数,所以可知{xn-1·xn+1+9}是一个完方数列.