数列通项公式解法探究

郑伟民

(福建省永春第四中学,福建 泉州 362608)

众所周知,数列是一个特殊的函数,函数的解析表达式是函数表示的一种类型.同样,数列的通项公式是数列最重要的表示.因为找到数列的通项公式可以给出数列的概貌,所以研究数列的通项公式非常重要.因此,在一些数列求解问题中,第一个小问题往往是找到一般项的公式.

1 Sn法

直接利用Sn定义求通项an,由Sn-Sn-1得到an的这种方法常用于已知数列前n和的通项公式求解题目.

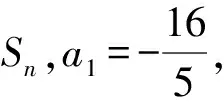
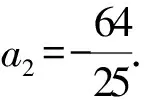
当n≥2时,由5an+1+Sn+16=0,

①

得5an+Sn-1+16=0.

②

①～②,得5an+1=4an.因为a2≠0,所以an≠0.

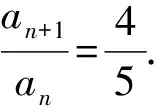
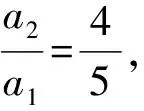
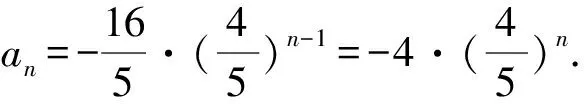
点评本题以数列前n项和为主要条件求解通项公式,可直接抓住an=Sn-Sn-1,可以便捷求出通项公式.

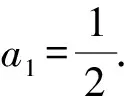
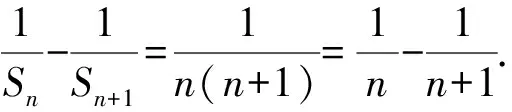
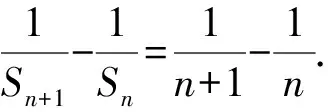
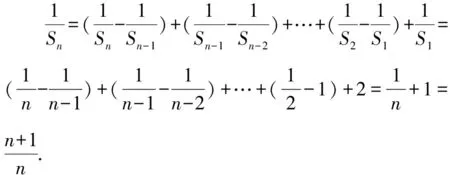
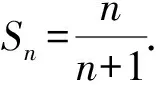
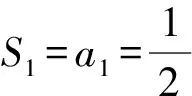
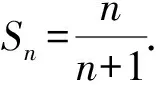
点评本题以递推公式f(Sn,an)=0为条件求解数列通项公式,将数列前n项和Sn转化为数列通项an,也可以将数列通项an转化为数列前n项和Sn,从而得到关于an(Sn)的递推关系,然后求出数列通项an.

2 数列前n项积Tn作商法

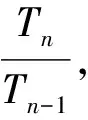
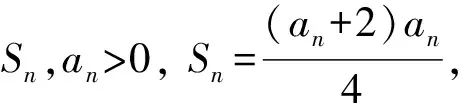
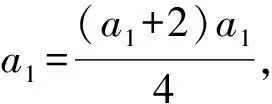
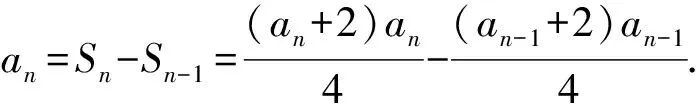
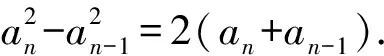
因为an>0,所以an-an-1=2.

所以数列{an}是首项为2,公差为2的等差数列,所以an=2+(n-1)×2=2n.

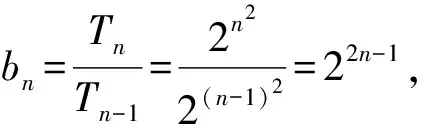
3 累加法

当an+1=an+f(n)且f(1)+f(2)+…+f(n)的和易求时,可将an+1=an+f(n)转化为an+1-an=f(n),结合累加法求解.

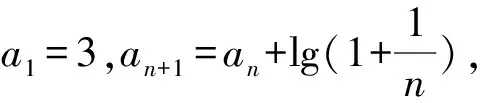
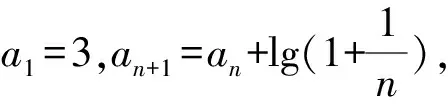
所以a10=a1+(a2-a1)+(a3-a2)+…+(a10-a9)=3+lg2-lg1+lg3-lg2+…+lg10-lg9=3-lg1+lg10=3+1=4.

4 累乘法

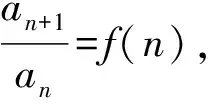
例5已知数列{an}满足a1=1,(2n-1)an+1=(2n+1)an.求{an}的通项公式.

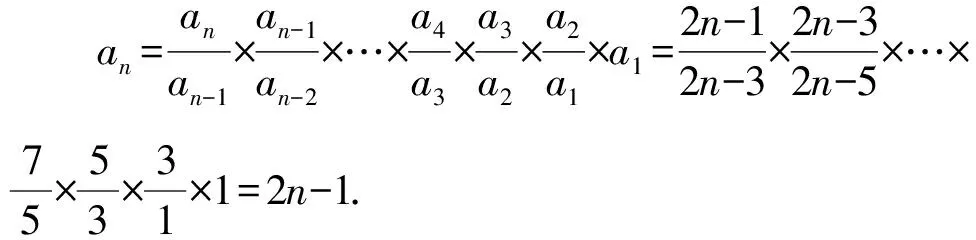
当n=1时,a1=1,符合上式,所以an=2n-1.

5 构造法

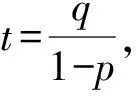
例6已知数列{an}中,a1=1,an+1=4an-6,则a2023=____.

分析由an+1=4an-6,得an+1-2=4(an-2).

而a1-2=-1,因此数列{an-2}是首项为-1,公比为4的等比数列,则an-2=-1×4n-1.即an=-4n-1+2.所以a2023=-42022+2.

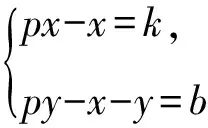
例7 在数列{an}中,a1=2,an+1=4an-3n+1,求数列{an}的通项an.

解析由an+1=4an-3n+1,得

an+1-(n+1)=4(an-n).

又a1-1=1,所以数列{an-n}是首项为1,公比为4的等比数列.所以an-n=4n-1.即an=4n-1+n.

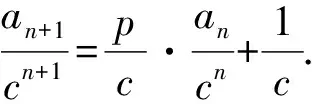
例8 已知数列{an}满足an+1=2an+4×3n-1,a1=1,求数列{an}的通项公式.

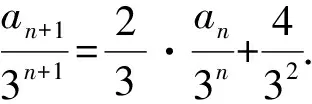
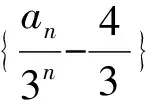
所以an=4×3n-1-3×2n-1.

6 结束语

本文梳理了通项公式的一些解法:Sn法、数列前n项积Tn作商法、累加法、累乘法、构造法.这些方法在数列通项求解中起到了化繁为简的作用,破解了数列通项的解题障碍点[1],值得我们深入研究,不断发现新问题,扎实基础,从而对这一专题熟练掌握.