将代数问题几何化的“魔术师”——向量

邵付松

(上海市零陵中学,上海 200032)

高中数学实验问题设计一直是高中数学教学研究的重要内容,这是因为只有精心创设的数学实验问题才有利于唤起学生的积极思维.设计的数学实验问题要具有可操作性、可探索性和层次性,问题的难度要适中,能产生悬念,才有利于激发学生去思考、观察,从实验问题中发现规律,提出猜想,进行探索与研究[1].通过教学建模、问题解决、理性思考和结论升华、变式探究、结论应用等环节,让学生亲历“提出问题—分析问题—解决问题—应用反思”的过程,使学生成为定理的发现者与再创造者,从而充分感受探究、创造的苦与乐[2].恰当地借助信息技术,能够帮助学生有效地建立起形与数的联系,指导学生学会利用几何图形等数学直观来描述问题、理解问题,运用空间想象认识事物,达成培育学生直观想象素养的目标.而实施的关键在于通过突破课堂新知难点,直观展现解决问题的关键环节,准确呈现完善学科知识结构[3].

1 问题引入

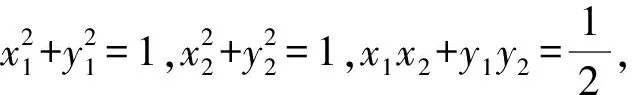
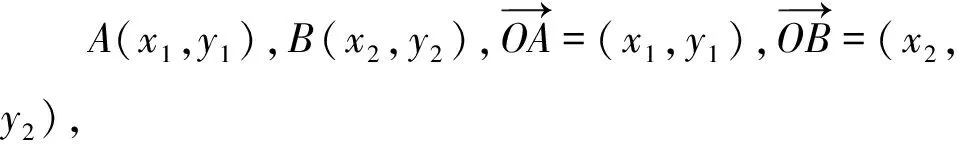
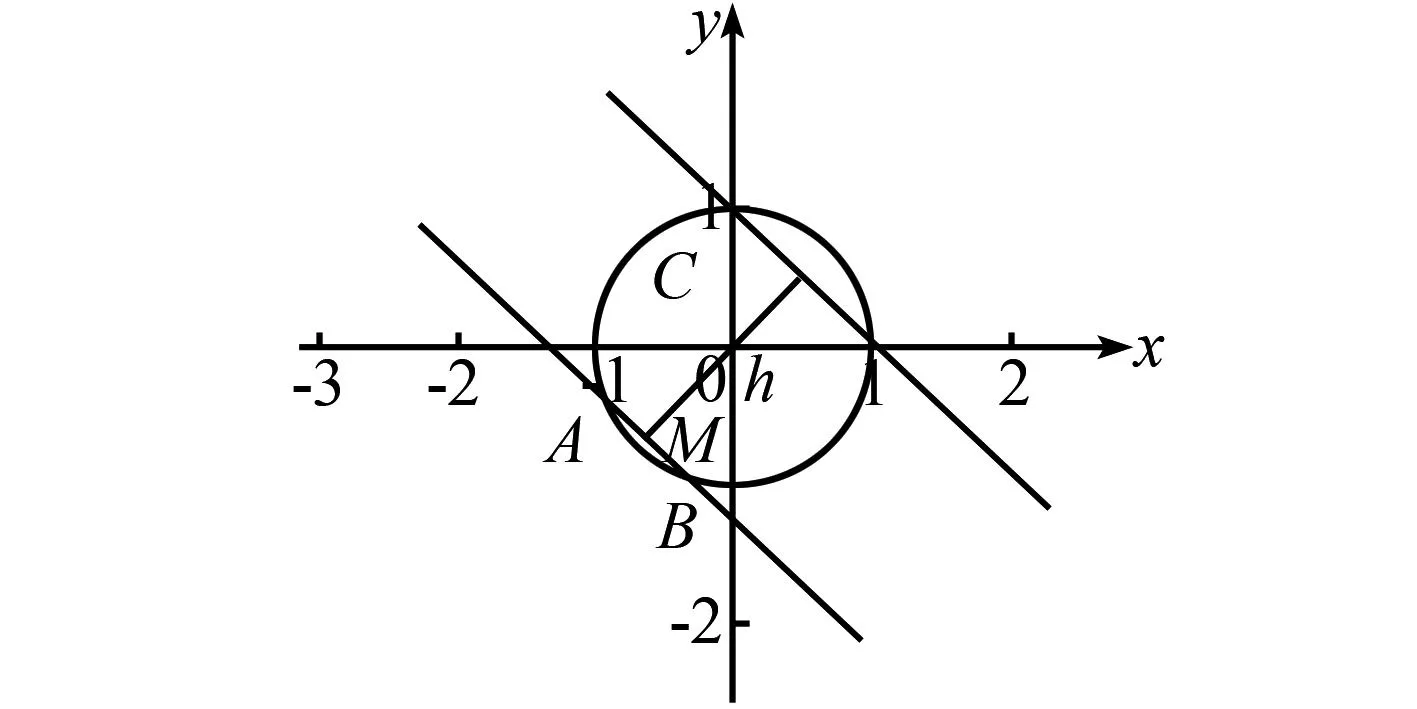
图1 点到直线的距离

这是2018年上海高考的第12题,从题目所在的位置上不难看出这道题的难度系数比较高,但当我们从向量的角度出发来分析这道题目时,却发现这道题没有想象中那么难,这就是向量方法的魅力所在,因此掌握好向量这个解题技巧对考生有莫大的帮助.

2 教学案例

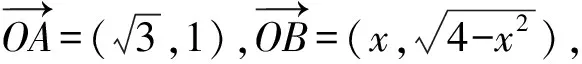
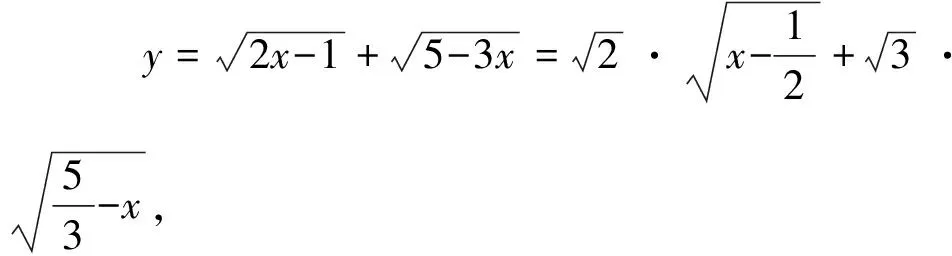
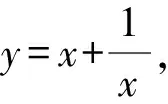
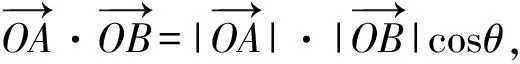
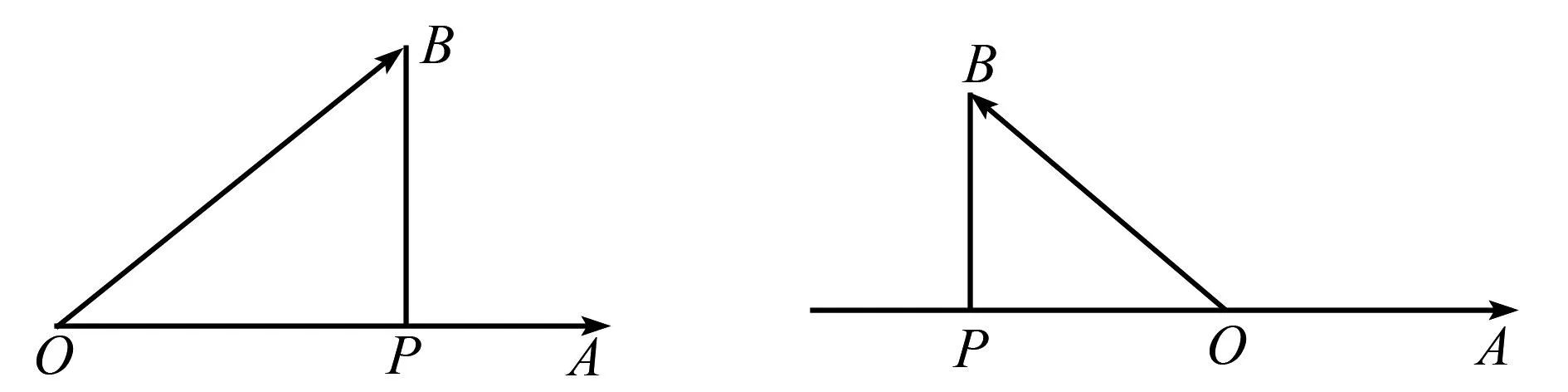
(a)正方向上的投影 (b)负方向上的投影图2 向量的投影

3 典型例题研究

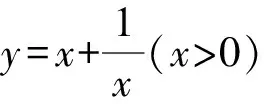
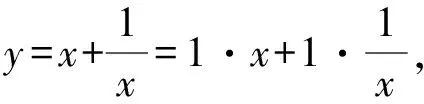
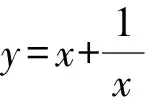
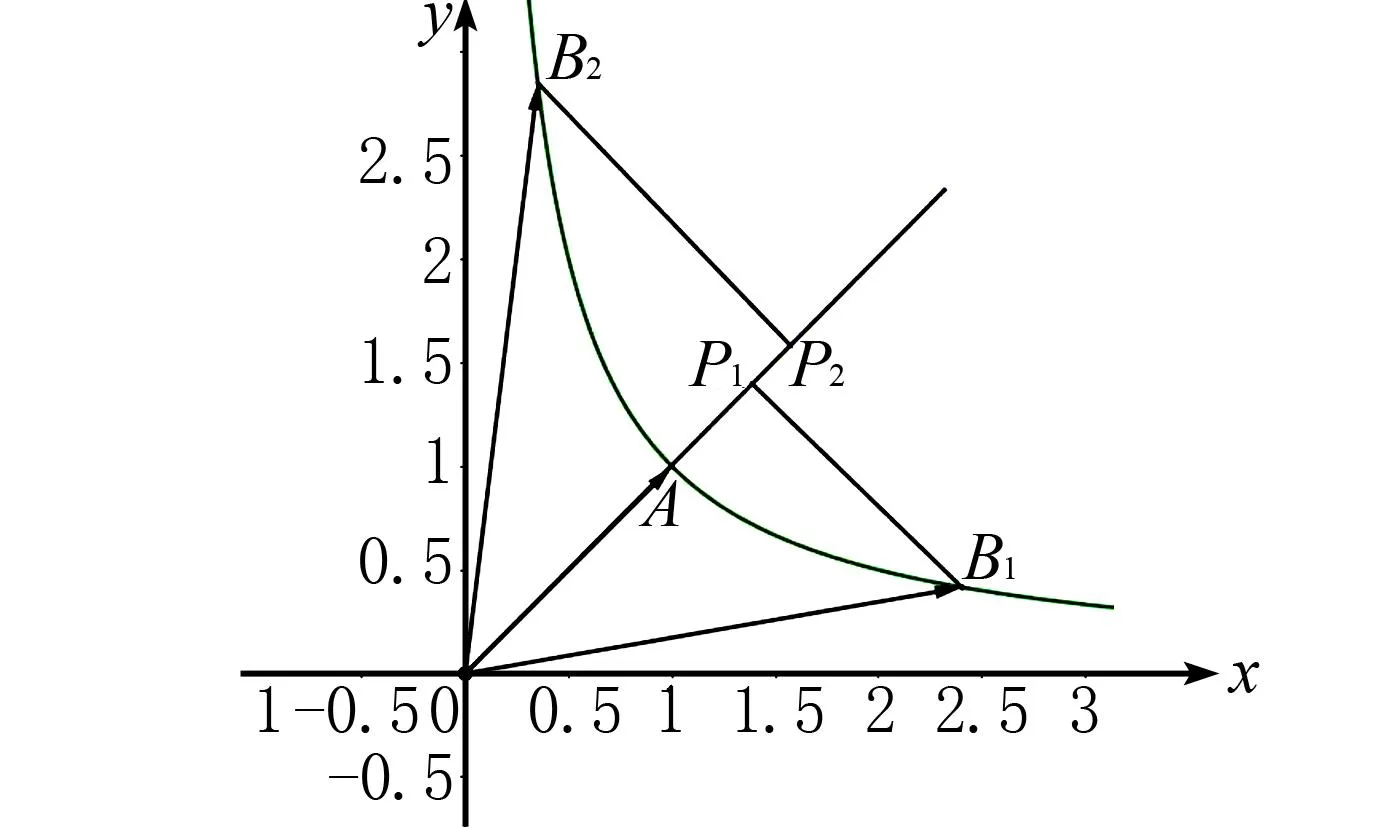
图3 耐克函数

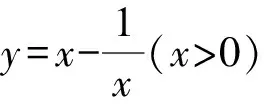
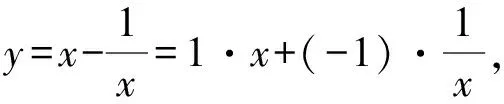
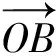
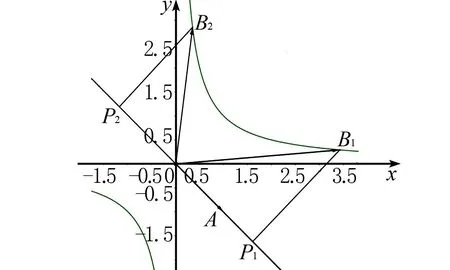
图4 飘带函数

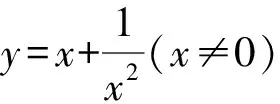
解析如图5所示,分析省略.

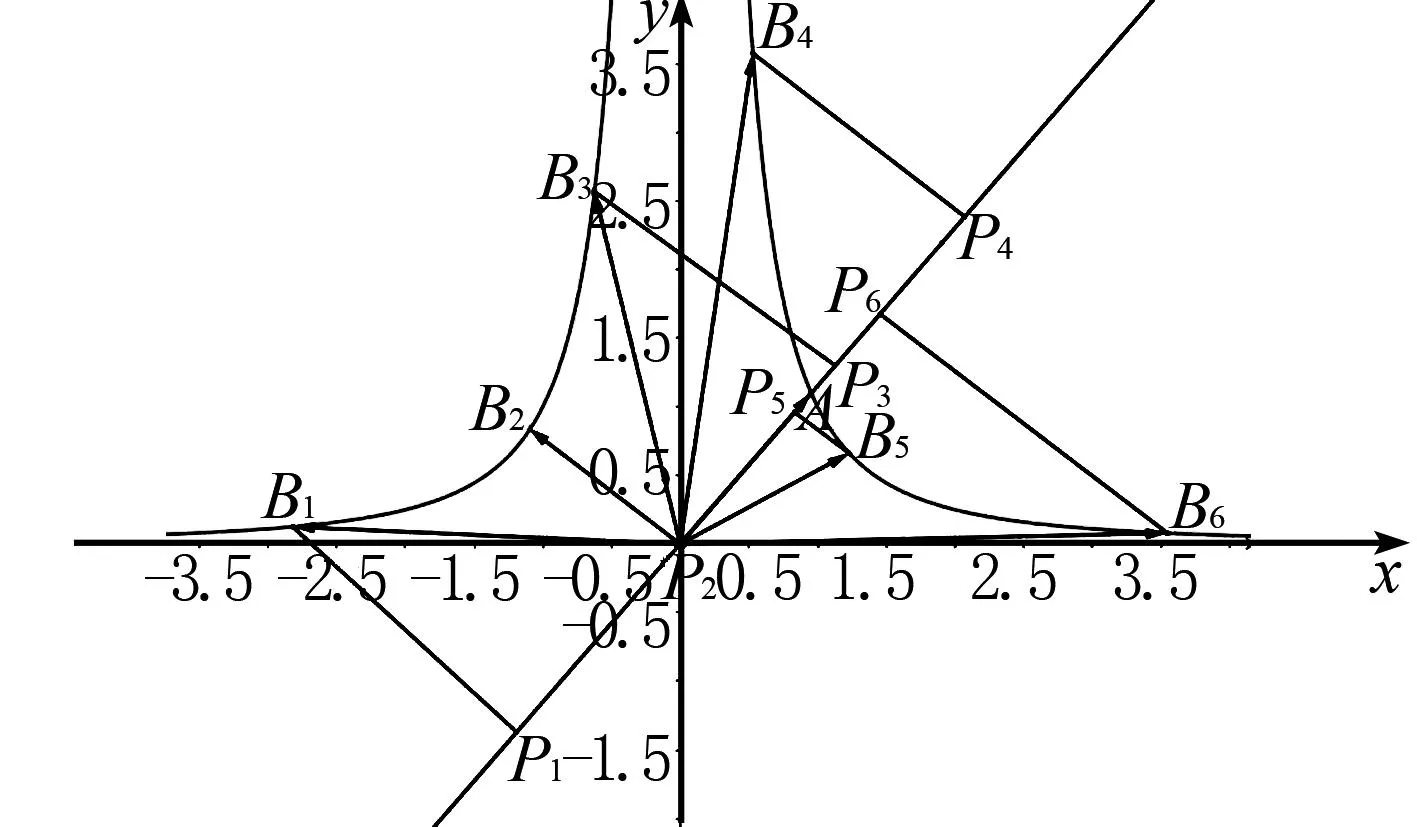
图5 幂和函数

3 结束语

向量作为分析代数问题的重要工具,在很多高难度的问题中都有广泛应用,因作者能力有限,这里不再进行推广.高中数学作为一门高中学段的基础学科,知识点之间存在许多奇妙的联系,希望本文能提供一个启发点,让更多的学者来一起进行探索,揭开高中数学神秘的面纱.