探究高中数学导数的解题方法

林超良

(泉州实验中学,福建 泉州 362000)

导数是高中数学的重要组成部分,也是高考数学的命题重点,对学生的综合运用能力要求比较高[1].熟练掌握导数解题方法,可以完善学生的知识框架、提高应用能力、培养自主探究习惯[2].本文以不同类型的数学导数题为例,探究、分析导数的解题方法,更好地发挥导数在高中数学解题中的作用.

1 求切线方程

导数的几何意义是“切点处导数等于切线斜率”.这一特征是求解函数切线方程的基础.求切线,需要两个要素.其一,切点坐标;其二,切线斜率.

例1已知函数f(x)=2sinx-xcosx-x,f′(x)为f(x)的导数.求曲线y=f(x)在点A(0,f(0))处的切线方程.

分析这道题的知识点是求在曲线上一点处的切线方程(斜率).先求出导函数,由k=f′(0)得到切线斜率,再根据点A坐标即可得到切线方程.

由题意f′(x)=cosx+xsinx-1,所以f′(0)=0,即切线的斜率k=0,且f(0)=0,所以曲线y=f(x)在点A(0,f(0))处的切线方程为y=0.

在解决切线方程的过程中,要注意以下几点:

(1)已知切点,求曲线的切线方程:已知切点(x0,y0),求出切点处的切线斜率f′(x0);

(2)过曲线上一点,求切线方程:过已知曲线上一点求切线方程,应注意到曲线上这一点,分为是切点和不是切点两种情况.

(3)过曲线外一点,求切线方程:这种情况和“过曲线上一点求切线方程”相似,都是先设出切点坐标,再进行切线方程的求解.

2 研究函数的单调性

在利用导数法判断函数单调性时,一般流程如下:首先求出函数的定义域,之后对函数求导,接着判断导函数的正负,最后通过导函数的正负,得出单调区间.

例2已知函数f(x)=xlnx-ax2,f′(x)为f(x)的导数,讨论f′(x)的单调性.

分析利用导数讨论函数的单调性,通常归结为求含参不等式的解集问题.含参一元二次不等式问题着重考查分类讨论思想,是高考命题中的重点和热点问题,而对含有参数的不等式问题,需要注意依据参数取值对不等式解集的影响进行分类讨论[3],解题时需要关注定义域及分类讨论的标准.

设g(x)=f′(x)=lnx-2ax+1,对g(x)求导,分a≤0和a>0讨论即可.

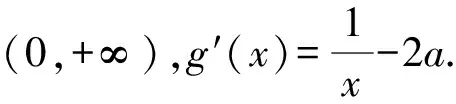
当a≤0时,g′(x)>0,g(x)在(0,+∞)上单调递增;

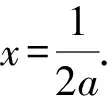
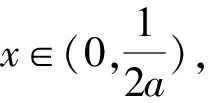
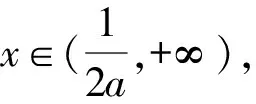
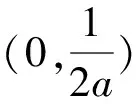
3 求函数的极值、最值

函数极值和值域问题是高考的重点和难点所在,考试大纲强调:重点考查利用导数的方法研究函数的单调性、极大(小)值、最大(小)值,研究方程和不等式.

解决极值和最值的主要流程是:(1)确定函数的定义域;(2)求导数f(x);(3)解方程f′(x)=0,求出函数定义域内的所有根;(4)列表检验f′(x)在f′(x)=0的根x0左右两侧值的符号,如果左正右负,那么f(x)在x0处取极大值,如果左负右正,那么f(x)在x0处取极小值.

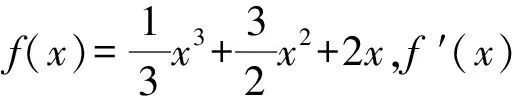
分析这道题的知识点是求已知函数的极值.求出函数的导数,进而求出函数的单调区间,从而结合极值的概念即可求出结果.

因为f′(x)=x2+3x+2=(x+1)(x+2),令f′(x)=0,得x1=-1,x2=-2,当x变化时,f′(x),f(x)的变化见表1:

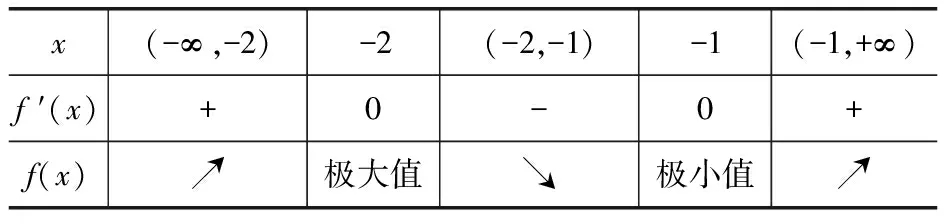
表1 x变化时,f ′(x),f(x)的变化表

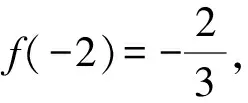
4 研究函数的图象

一般而言,作函数图象有以下流程:先求出函数的定义域,接着判断函数的周期性和奇偶性,求出函数的零点、函数与y轴的交点等特殊点,之后确定函数的单调区间和极值点,最后根据上述结论精细绘制函数的大致图象.

例4 函数f(x)=xsinx+cosx的导数f′(x)的部分图象大致为( ).

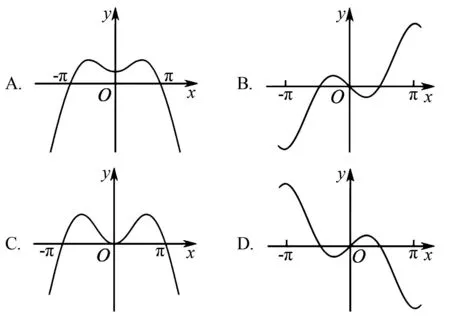
图1 例4题图

分析根据已知,利用函数的求导公式以及函数的奇偶性、函数值进行排除.

因为f(x)=xsinx+cosx,

所以f′(x)=sinx+xcosx-sinx=xcosx.

令g(x)=f′(x)=xcosx,x∈R,则g(-x)=-xcosx=-g(x),所以函数g(x)=xcosx是奇函数,A,C错误;又g(π)=πcosπ=-π<0,B错误.故选D.

导数作为解决函数的一个重要工具,其主要目的就是判断并确定函数的单调区间,进而得出函数增减的大致情况,再依据函数的性质解决实践问题,才能更好地理解以后的放缩问题.

5 求参数取值范围

解决参数取值范围问题可以根据导函数确定函数的单调性和极(最)值,大致绘制函数图象的趋势,再运用数形结合分析问题(或结合图象特征分析零点的位置)转化为关于参数的不等式组,通过解不等式组求出参数的取值范围.

例5已知函数f(x)的导数f′(x)=a(x+1)·(x-a),若f(x)在x=-1处取到极大值,则a的取值范围是多少?

分析这道题分a=0,a>0和a<0三种情况,结合二次函数的图象性质与极值的定义即可判断.由题意当a=0时不成立,当a≠0时f′(x)有两个零点x=-1与x=a.

①当a>0时,f′(x)开口向上,且-10,x∈(-1,a)时f′(x)<0,所以f(x)在x=-1处取到极大值;

②当a<0时,f′(x)开口向下.当a=-1时,f′(x)≤0,f(x)单调递减,f(x)无极大值;当a<-1时,在区间x∈(a,-1)上f′(x)>0,x∈(-1,+∞)上f′(x)<0,故f(x)在x=-1处取到极大值;

当-10,故f(x)在x=-1处取到极小值.

综上有a>0或a<-1.

6 解不等式

利用导数证明不等式通常有如下流程:首先,构造新函数F(x),接着通过导数解析函数F(x)的单调区间,最后通过判断定义域内F(x)与0的大小关系来证明不等式.这类题目重点在于灵活准确地构造函数,再利用函数解不等式.

例6已知函数f(x)的导数为f′(x),且(x+1)f(x)+xf′(x)≥0对x∈[0,+∞)恒成立,则下列不等式一定成立的是( ).

A.f(1)>2ef(2) B.3f(2)>2ef(3)

C.2f(1)

分析这道题的考点为用导数判断或证明已知函数的单调性.设g(x)=xexf(x),则g′(x)=ex[(x+1)f(x)+xf′(x)]≥0,所以函数g(x)单调递增.g(2)=2e2f(2)>g(1)=ef(1),即f(1)<2ef(2),故A,C错误;g(2)=2e2f(2)

从上述解题步骤可看出,构造新函数是利用导数证明不等式最重要的环节,之后在相应区间上判断单调性,最后形成结论.事实上,解题过程中常会综合用到多种方法,教师应指导学生灵活应用所学知识,树立运用多种方法解决问题的意识,能够把复杂问题简单化.

7 结束语

综上可知,导数涵盖了多元化的逻辑思维,可以丰富学生的解题思路,解答题目更便捷,促进学习效率提升.若要使导数的价值和作用发挥至最大,学生必须深入理解导数知识点,熟练掌握导数基础知识和变换形式,在不断练习中巩固技能,切实做到活学活用,提升解题效率.