基于互信息和融合加权的并行深度森林算法
毛伊敏 李文豪


收稿日期:2023-05-18;修回日期:2023-07-26 基金項目:广东省重点领域研发计划资助项目(2022B0101020002);广东省重点提升项目(2022ZDJS048)
作者简介:毛伊敏(1970—),女,新疆伊犁人,教授,博导,博士,主要研究方向为分布式计算和人工智能(mymlyc@163.com);李文豪(1997—),男(通信作者),江西宜春人,硕士研究生,主要研究方向为大数据和机器学习.
摘 要:针对大数据环境下并行深度森林算法中存在不相关及冗余特征过多、多粒度扫描不平衡、分类性能不足以及并行化效率低等问题,提出了基于互信息和融合加权的并行深度森林算法(parallel deep forest algorithm based on mutual information and mixed weighting,PDF-MIMW)。首先,在特征降维阶段提出了基于互信息的特征提取策略(feature extraction strategy based on mutual information,FE-MI),结合特征重要性、交互性和冗余性度量过滤原始特征,剔除过多的不相关和冗余特征;接着,在多粒度扫描阶段提出了基于填充的改进多粒度扫描策略(improved multi-granularity scanning strategy based on padding,IMGS-P),对精简后的特征进行填充并对窗口扫描后的子序列进行随机采样,保证多粒度扫描的平衡;其次,在级联森林构建阶段提出了并行子森林构建策略(sub-forest construction strategy based on mixed weighting,SFC-MW),结合Spark框架并行构建加权子森林,提升模型的分类性能;最后,在类向量合并阶段提出基于混合粒子群算法的负载均衡策略(load balancing strategy based on hybrid particle swarm optimization algorithm,LB-HPSO),优化Spark框架中任务节点的负载分配,降低类向量合并时的等待时长,提高模型的并行化效率。实验表明,PDF-MIMW算法的分类效果更佳,同时在大数据环境下的训练效率更高。
关键词:Spark框架;并行深度森林;互信息;负载均衡
中图分类号:TP311 文献标志码:A
文章编号:1001-3695(2024)02-023-0473-09
doi:10.19734/j.issn.1001-3695.2023.05.0240
Parallel deep forest algorithm based on mutual information and mixed weighting
Mao Yimin1,2,Li Wenhao1
(1.School of Information Engineering,Jiangxi University of Science & Technology,Ganzhou Jiangxi 341000,China;2.School of Information Engineering,Shaoguan University,Shaoguan Guangdong 512000,China)
Abstract:
In the context of big data environments,the parallel deep forest algorithm faces several challenges,such as an abundance of irrelevant and redundant features,imbalanced multi-granularity scanning,inadequate classification performance,and low parallelization efficiency.To tackle these issues,this paper proposed PDF-MIMW.Firstly,the algorithm introduced FE-MI in the phase of dimensionality reduction,which filtered the original feature set by combining feature importance,interaction,and redundancy metrics,thereby eliminating excessive irrelevant and redundant features.Next,the algorithm proposed an IMGS-P in the phase of multi-granularity scanning,which involved padding the reduced features and performing random sampling on the subsequences obtained after window scanning,thereby ensuring a balanced multi-granularity scanning process.Then,the algorithm put forth the SFC-MW in the phase of cascade forest construction,which utilized the Spark framework to parallelly construct weighted sub-forests,thereby enhancing the models classification performance.Finally,the algorithm designed a load balancing strategy based on a mixed particle swarm algorithm in the phase of class vector merging,which optimized the load distribution among task nodes in the Spark framework,reducing the waiting time during class vector merging and improving the parallelization efficiency of the model.Experiments demonstrate that the PDF-MIMW algorithm achieves superior classification performance and higher training efficiency in the big data environment.
Key words:Spark framework;parallel deep forest;mutual information;load balance
0 引言
深度森林(deep forest,DF)算法[1]是一种基于深度模型提出的级联随机森林算法,与深度神经网络相比具有更少的超参数,更低的数据需求量以及自适应的模型复杂度,并且具有较好的鲁棒性和泛化能力,因而被广泛应用于目标识别[2]、图像处理[3]、文本识别[4]、故障诊断[5]、网络入侵检测[6]、医学诊断[7]等领域。近年来,随着网络与信息技术的发展,大数据成为了当前的研究热点,日益增长的数据规模和不断变化的数据模态使得传统DF算法在处理大数据时存在不相关及冗余特征过多、分类性能不足以及并行化效率低的问题。因此,设计适用于处理海量数据的DF算法意义重大。
近年来,随着大数据分布式计算框架在DF算法上的广泛应用,加州大学伯克利分校的AMP实验室提出的Spark[8]分布式计算模型因其运行速度快、简单易用、通用性强、运行模式多样等特点受到了广大学者的青睐。例如Zhu等人[9]提出了一种并行DF算法ForestLayer,该算法将级联层中的森林分解为子森林后采用并行计算的方式对各子森林模型进行训练,提高了模型的训练效率,降低了通信开销,同时提出了延迟扫描、预池化和部分传输三种方法优化算法性能。在此基础上,Chen等人[10]提出了BLB-gcForest(bag of little bootstraps-gcForest)算法,該算法通过自适应的森林分解能够寻找到最优子森林分解粒度,从而减少模型的超参数并提升模型的训练效率。为进一步提升模型的训练效率,毛伊敏等人[11]则在级联森林构建阶段引入了权重分配的思想,提出了结合信息论改进的DF算法(improved parallel deep forest based on information theory,IPDFIT),该算法通过对训练样本进行评估以决定样本是否进入下一级的训练从而减少了样本数量,提升了模型的并行训练效率。尽管以上三种并行DF算法对模型的训练效率均有提升,但是依旧存在以下四个方面的不足:a)在特征降维阶段,由于原始数据集规模庞大且维度高,若不对其进行必要的筛选,将会给模型训练带来不相关和冗余特征过多的问题;b)在多粒度扫描阶段,窗口扫描会使数据集中靠近两端的特征被扫描的次数减少,导致多粒度扫描不平衡的问题;c)在级联森林构建阶段,由于森林中每个决策树的分类能力各不相同,对每棵树的结果进行简单算术平均会影响模型整体的分类性能;d)在类向量合并阶段,由于各任务节点的负载没有得到合理分配,当类向量合并时会出现节点之间互相等待的情况,从而导致模型并行化效率低的问题。
针对以上问题,本文提出了基于互信息和融合加权的并行DF算法——PDF-MIMW,算法的主要工作如下:a)提出了基于互信息的特征提取策略FE-MI,通过对特征重要性和特征之间的交互性及冗余性进行度量以过滤不相关和冗余特征,解决了不相关和冗余特征过多的问题;b)提出了基于填充的改进多粒度扫描策略IMGS-P,通过对原始特征集进行填充,并对滑动窗口扫描后的特征子序列进行随机采样,解决了多粒度扫描不平衡的问题;c)提出了基于融合加权的并行子森林构建策略SFC-MW,结合Spark分布式框架进行子森林的并行化构建,并赋予分类能力强的子森林更高的权重,解决了大数据环境下模型分类性能不足的问题;d)提出了基于混合粒子群算法的负载均衡策略LB-HPSO,通过对级联森林中并行训练的任务节点进行负载分配寻优以提升类向量并行合并的效率,解决了大数据环境下并行化效率低的问题。
1 相关概念介绍
1.1 互信息、联合互信息与交互信息
互信息[12]通常用于衡量两个随机变量之间的相关性,该值越大代表两个随机变量的相关性越高,反之越低。假设X和Y是两个离散型随机变量,则X和Y之间的互信息I(X;Y)为
I(X;Y)=H(X)+H(Y)-H(X,Y)(1)
其中:H(X)和H(Y)分别X和Y的熵;H(X,Y)为两者的联合熵;当Y为标签或者类属性时,I(X;Y)即为信息增益。
联合互信息[12]通常用于表示随机变量与目标变量之间的关系。假设X、Y和Z是三个离散型随机变量,则X、Y和Z之间的联合互信息I(X,Y;Z)的定义为
I(X,Y;Z)=H(X,Y)-H(X,Y|Z)(2)
其中:H(X,Y|Z)为X、Y和Z之间的条件互信息。
交互信息[12]通常用于衡量三个随机变量之间的交互作用。假设X、Y和Z是三个离散型随机变量,其交互信息可定义为
I(X;Y;Z)=I(X,Y;Z)-I(X;Z)-I(Y;Z)(3)
1.2 对称不确定性
对称不确定性[13]是为了消除变量单位和变量值的影响所采用的规范化信息增益。假设X和Y是两个离散型随机变量,则其对称不确定性SU(X,Y)的定义为
SU(X,Y)=2I(X;Y)H(X)+H(Y)(4)
其中:H(X)和H(Y)分别为X和Y的信息熵;I(X;Y)为X和Y之间的互信息。
1.3 PSO算法
PSO算法(particle swarm optimization)[14]是通过模拟鸟群捕食行为设计的一种全局随机搜索算法,可以对粒子的位置进行不断的调优,从而寻求最优解。该算法中粒子在搜索空间中以一定速度飞行,并且会根据当前最优粒子位置和自身的飞行经验进行调整。PSO算法主要包括粒子位置和速度的初始化、粒子的速度更新以及粒子的位置更新三个阶段。假设在D维空间中有N个粒子,具体流程如下:
a)初始化粒子的位置和速度。
xi=(xi,1,xi,2,…,xi,D)(5)
vi=(vi,1,vi,2,…,vi,D)(6)
b)粒子的速度更新。假设pbesti,d为粒子个体经历过的最好位置,gbestd为种群经历过的最好位置,f为粒子的自适应值,则粒子的速度更新如下所示。
pbesti,d=(pi,1,pi,2,…,pi,D)(7)
gbestd=(g1,g2,…,gD)(8)
vki,d=ωvk-1i,d+c1r1(pbesti,d-xk-1i,d)+c2r2(gbestd-xk-1i,d)(9)
其中:i為粒子的序号;d为粒子的维度;ω为惯性权重,表示之前的速度对当前速度的影响;c1和c2是学习因子;r1和r2是两个随机数,取值为[0,1]。
c)粒子的位置更新。假设xk-1i,d为粒子当前位置,vk-1i,d为粒子当前更新速度,则粒子的位置更新为
xki,d=xk-1i,d+vk-1i,d(10)
2 PDF-MIMW算法
本文提出的PDF-MIMW算法主要包含特征降维、多粒度扫描、级联森林构建以及类向量合并四个阶段。首先,在特征降维阶段提出了FE-MI策略,通过袋外数据误差对于输入的原始特征集进行重要性划分,并根据特征之间的冗余性和交互作用过滤冗余特征,获得高相关度和低冗余度的特征集;其次,在多粒度扫描阶段提出了IMGS-P策略,对精简后的特征集进行填充并对滑动窗口扫描后的特征子序列进行随机采样,保证多粒度扫描的平衡;接着,在级联森林构建阶段提出SFC-MW策略,结合Spark框架并行构建子森林,并依据子森林的准确率赋予相应的权重,提升模型的分类性能;最后,在类向量合并阶段提出LB-HPSO策略,采用改进的粒子群算法对Spark框架中每个任务节点的负载分配情况进行优化,降低类向量合并时的等待时长,提升模型的并行效率。算法的系统处理框架如图1所示。
2.1 特征降维
目前在大数据环境下的并行DF算法中,原始特征集通常包含大量不相关和冗余特征,因此本文在特征降维阶段提出基于互信息的特征提取策略FE-MI,该策略综合考量特征重要性、特征冗余性和特征之间的交互程度三方面对特征进行处理。该策略主要包含两个步骤:a)特征划分。提出基于袋外数据误差[15]的特征重要性度量(feature important measure,FIM),通过衡量特征的重要性对原始特征集进行初步划分;b)特征过滤。提出了基于互信息的特征交互系数(feature interaction coefficient,FIC)和特征评价系数(feature evaluating coefficient,FEC),通过对特征交互性和冗余性两个维度进行衡量[16],进一步过滤真实冗余特征。
2.1.1 特征划分
在进行特征过滤之前,需要先对特征集进行粗略的划分,具体过程如下:首先在样本上训练得到随机森林模型,对模型中每一棵决策树选择相应的袋外数据计算模型的袋外数据误差Errt,对特征X进行随机扰动后再次计算袋外数据误差Errt(Xi);接着提出基于袋外数据误差的特征重要性度量FIM来筛选优势特征,计算原始特征集R中各特征的特征重要性度量FIM,并根据特征重要性度量FIM的大小进行降序排序;最后依据特征重要性度量FIM的大小,按照比例β从高到低将原始特征集R中的特征划分为优势特征集与候选特征集两部分。
定理1 特征重要性度量FIM。已知随机森林中决策树的数目为n,则特征Xi的特征重要性度量FIM为
FIC=IM(Xi)norm(11)
其中:IM(Xi)为特征Xi扰动前后的平均袋外误差变化;norm为特征重要性的归一化因子。
证明 假设Errt表示在随机森林的第t棵决策树中,选择相应的袋外数据计算的袋外数据误差,在特征Xi处加入随机噪声后重新计算的袋外数据误差为Errt(Xi)。因此改变特征Xi处取值后对该决策树准确率的影响为
Errt(Xi)-Errt(12)
由于在随机森林算法中,特征越重要,改变测试数据中样本在该特征处的值时,所得到的预测误差会越大。所以代表在随机森林模型中特征Xi的重要性度量可对随机森林中每棵树进行袋外数据误差预测并取其均值得到
IM(Xi)=1n∑nt=1(Errt(Xi)-Errt)(13)
最后将特征重要性IM(Xi)的值域规范至[0,1],采用归一化因子得到
FIM=1n∑nt=1(Errt(Xi)-Errt)(IM(Xi)-IM)-min(IM(Xi)-IM)max(IM(Xi)-IM)-min(IM(Xi)-IM)=
IM(Xi)norm(14)
综上,当FIM偏大时,表明当前特征Xi具有较高的重要性,反之则较低。证毕。
因此,通过比较FIM数值的大小可以将各特征按照重要性进行排序。
2.1.2 特征过滤
经过特征划分后,特征集中仍残留大量的冗余特征,因此还需要对其中的冗余特征进行过滤,具体过程如下:首先提出基于互信息的特征交互系数FIC来衡量特征之间的交互程度,接着提出特征评价系数FEC从特征之间的交互性和冗余性两个维度对特征进行评价从而过滤冗余特征,计算当前两个特征集中各特征的特征评价系数FEC;接着依据特征评价系数FEC的大小对各特征进行升序排序,按从高到低分别从优势特征集中提取k个特征,从候选特征集中提取m-k个特征;最后将从两个特征集提取的特征合并成含有m个特征的最终特征集D。
定理2 特征交互系数FIC。已知有特征集F={X1,X2,…,Xi},特征Xi与Xj同为特征集F中的特征,Z为样本标签,则特征Xi的特征交互系数FIC为
FIC(Xi)=1F∑FXi∈F,Xj≠XiW(Xi)×score(Xi;Xj)(15)
其中:W(Xi)为特征Xi在特征交互评价中所占的权重;score(Xi;Xj)为特征Xi、Xj与样本标签Z三者的归一化交互信息系数。
证明 已知特征Xi与Xj同為特征集F={X1,X2,…,Xi}中的特征,Z为样本标签,在特征交互中,特征Xi与Xj与样本标签Z三者之间的交互信息可以表示为I(Xi;Xj;Z),将交互信息的值域规范至[-1,1]可以获得归一化后的交互信息系数:
score(Xi;Xj)=I(Xi;Xj;Z)H(Xi)+H(Xj)(16)
特征Xi与标签Z之间的互信息和特征Xj与标签Z之间的互信息则分别为I(Xi;Z)、I(Xj;Z)。 由于互信息可用于衡量特征与标签之间的关联程度,所以特征Xi在特征交互评价中所占的权重比可以表示为
W(Xi)=I(Xi;Z)I(Xi;Z)+I(Xj;Z)(17)
可得: W(Xi)×score(Xi;Xj)=I(Xi;Z)I(Xi;Z)+I(Xj;Z)×I(Xi;Xj;Z)H(Xi)+H(Xj)(18)
由于交互信息系数score(Xi;Xj)<0表示对于样本标签Z,随机变量Xi和Xj两者相互作用会带来信息冗余,score(Xi;Xj)=0代表两者相互独立,score(Xi;Xj)>0代表两者相互作用能够带来信息增益,W(Xi)则代表了特征Xi在特征交互评价中的占比,所以两者的乘积W(Xi)×score(Xi;Xj)则表示特征Xi的特征交互程度,当存在信息增益W(Xi)×score(Xi;Xj)较大,反之则较小。最后对特征集F={X1,X2,…,Xi}中的其他各特征求均值,能够得到特征Xi的特征交互系数计算公式:
FIC(Xi)=1F∑|F|Xi∈F,Xj≠XiI(Xi;Z)I(Xi;Z)+I(Xj;Z)×I(Xi;Xj;Z)H(Xi)+H(Xj)=
1F∑|F|Xi∈F,Xj≠XiW(Xi)×score(Xi;Xj)(19)
综上,当FIC偏大时,表明特征Xi与其他各特征之间的交互程度更大,反之则更小。证毕。因此,可以通过计算特征之间的FIC值来衡量特征之间的交互程度。
定理3 特征评价系数FEC。已知特征Xi为特征集F={X1,X2,…,Xi}中的特征,且特征Xi的特征交互系数为FIC,则其特征评价系数FEC为
FEC(Xi)=αRED(Xi)-FIC(Xi)(20)
其中:FIC为特征交互系数;RED为特征冗余系数;α为常数系数项。
证明 已知对称不确定性SU(Xi,Xj)可用于衡量两个随机变量的关联程度,则 SU(Xi,Xj)可以表示特征Xi与Xj之间的关联程度,因此对特征集F={X1,X2,…,Xi}中其他特征取均值可获得特征Xi与其他特征之间的平均关联程度:
RED(Xi)=1|F|∑Xi∈F,Xj≠XiSU(Xi,Xj)(21)
该值越大代表特征Xi与其他特征之间的关联程度越高,即特征Xi与其他特征之间存在的冗余越大,反之则越小。而该特征Xi对应特征交互系数FIC的大小反映的是对于样本标签Z,当前特征Xi与特征集F中其他特征之间的交互程度,即该数值越大其交互程度也就越高,反之越低。故而,能够通过结合特征之间的交互程度和冗余程度对各特征的真实冗余程度进行评价,即得到:
FEC(Xi)=1F∑|F|Xi∈F,Xj≠XiαSU(Xi,Xj)-W(Xi)score(Xi;Xj)(22)
综上,当FEC偏大时,表明特征Xi与其他特征之间的真实冗余程度越高,反之则越低。证毕。
因此,可以通过计算特征图之间的FEC值来过滤掉冗余程度较高的特征。
算法1 FE-MI策略
输入:原始数据集R;特征划分比例β;过滤系数m和k。
输出:最终特征集D。
a)特征划分
for特征Xi in R do
计算袋外数据误差Errt(Xi)
对Xi进行干扰
计算干扰后Xi的袋外数据误差Errt(Xi)
依据Errt和Errt(Xi)计算特征重要性度量FIM
end for
依照特征重要性度量FIM进行排序
依据设置的比例β将原始特征集中的特征划分至优势特征集P和候选特征集C
b)特征过滤
for优势特征集P和候选特征集C中的特征Xido
计算特征交互系数FIC 和特征评价系数 FEC
end for
依照特征评价系数FEC进行排序
从优势特征集P中选取前k个特征,从候选特征集C中选出前m-k个特征
将这m个特征合并至特征集 D
return D
2.2 多粒度扫描
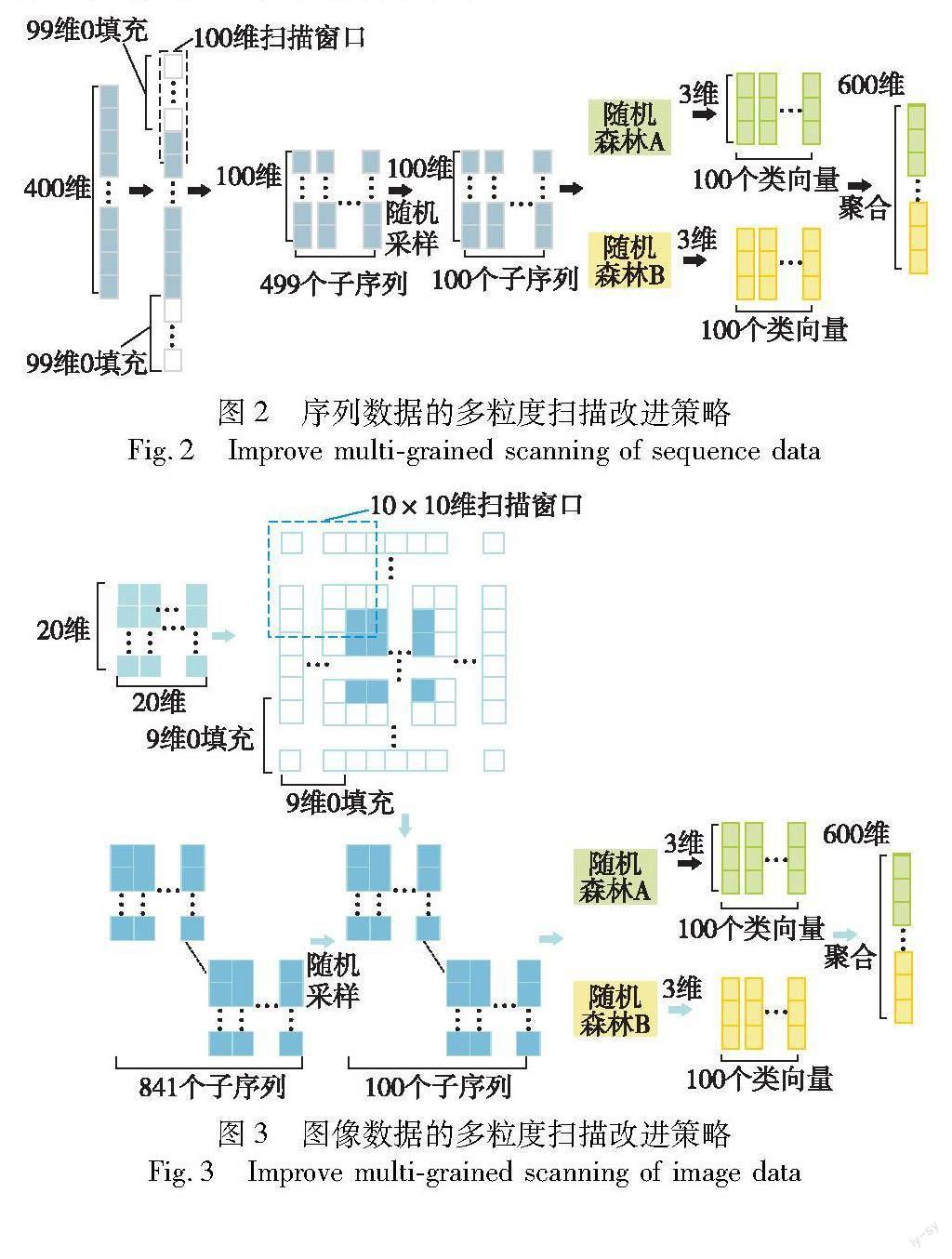
针对多粒度扫描过程中产生的特征扫描不平衡问题[17],本文提出了基于填充的改进多粒度扫描策略。该策略具体流程如下:首先对特征集进行补零填充,若为序列数据,则对其首尾进行0填充,若扫描的窗口大小为n,则上下填充的数量为n-1,若为图像数据,则对四周进行0填充,若扫描的窗口大小为n×n,则四周填充的数量为n-1;其次,用一定大小的滑动窗口分别对填充后的特征集进行扫描,以获得多个窗口大小的特征子序列,随后对特征子序列进行随机采样;最后将采样后的特征子序列分别输入至1个随机森林和1个完全随机森林训练,并将两个森林的训练结果进行拼接得到最终的输入特征集。改进的多粒度扫描过程如图2、3所示。
算法2 IMGS-P策略
输入:最终特征集D。
输出:输入特征集α。
for最终特征集D中的数据do
对数据进行补0填充
end for
确定多粒度扫描的窗口大小
for填充后的数据 do
进行多粒度扫描
end for
对特征子序列进行随机采样
输出采样后特征子序列
将采样后特征子序列分别输入至1个随机森林和1个完全随机森林进行训练
输出随机森林和完全随机森林的结果
将随机森林输出的结果和完全随机森林输出的结果进行拼接得到类向量α
return α
2.3 级联森林构建
在目前的并行DF算法中,获取级联森林的预测结果是通过对随机森林中每棵决策树的预测结果取均值。然而,由于森林中各个决策树的分类能力是各不相同的,简单地对所有决策树的预测结果进行算术平均会影响模型的分类性能,从而导致模型在级联森林并行构建时容易出现分类性能不足的问题[18]。所以本文结合Spark提出并行子森林构建策略,通过融合加权的方式赋予分类能力强的子森林更高的权重,从而提升模型整体的分类性能。该策略主要包括三个步骤:a)森林分解。依据随机状态对随机森林进行分解,保持森林分解前后的一致性。b)权重分配:分别赋予样本和子森林初始权重,并将样本输入子森林进行训练,获得融合迭代后的子森林权重。c)森林构建:结合Spark并行框架实现级联森林的并行构建,对分类结果进行交叉验证以决定是否终止训练。
2.3.1 森林分解
由于级联森林中随机森林的数量较少,如果以随机森林为单位进行权重分配,则难以提高模型的分类能力[19]。所以本文采用基于随机状态的森林分解策略对随机森林进行分解,以子森林为单位进行权重分配。其具体过程为:首先遍历级联森林层中i个随机森林R1,R2,…,Ri,获得其随机状态参数r10,r20,…,ri0,则第i个随机森林中的k棵决策树的随机状态参数分别为ri1,ri2,…,rik;接着将该随机森林分解为p个子森林sfi1,sfi2,…,sfip,其中每个子森林都包含l棵决策树;最后为随机森林Ri中每一个子森林设置随机状态ri0,ril,…,rik-l。
子森林随机状态参数的设置方法如图4所示。假设随机森林模型R中共有7棵决策树,将该森林分为子森林sf1、sf2、sf3,分别含有2、2、3棵樹。如果随机森林R的随机状态为r0,则其中每棵树的随机状态分别按顺序生成为r1,r2,…,r7。对于分解后的子森林,可以将子森林sf1的初始随机状态设为r0,则其中2棵决策树的初始随机状态会按顺序生成为r1、r2。接着将子森林sf2的初始随机状态设为r2,则其中2棵决策树的初始随机状态会按顺序生成为r3、r4,同理将子森林sf3的初始随机状态设为r4,其中3棵决策树的初始随机状态会生成为r5、r6、r7。因此,随机森林分解后每棵树的随机状态与其不分解时的随机状态完全相同。由于随机森林中每棵树的训练结果都是由其初始随机状态决定的,所以对于分解前后的随机森林,输入相同特征所产生的类向量也会完全相同。
2.3.2 权重分配
使用子森林分解策略对随机森林进行分解得到子森林和相应的随机状态后,便可对子森林进行权重分配,具体过程如下:首先读取袋外数据集(out of bag,OOB)作为子森林的权重计算的样本,同时为每个样本和每个子森林赋予相同的权重向量;接着提出层级预测矩阵(layer prediction matrix,LPM)对层级中子森林的预测结果正确与否进行判别;最后提出融合权重公式(mixed weighting formula,MWF)对样本和子森林的权重进行迭代计算直至收敛,赋予子森林最终收敛的权重值。
定理4 层级预测矩阵LPM。已知C为训练样本集T的类别矩阵,则层级预测矩阵LPM为
LPM=[Pre(S1,T)==CT,Pre(S2,T)==CT,…,Pre(Sn,T)==CT](23)
其中: Pre(Sk,T)=arg max(p1,1p1,2…p1,c)
arg max(p2,1p2,2…p2,c)
arg max(pm,1pm,2…pm,c)(24)
其中:m为样本个数,c为类别个数,记为L={l1,l2,…,lc},Sk(k∈[1,n])表示第k个子森林,pi,j为第i个训练样本被子森林Sk预测为类lj的概率。
证明 设子森林Sk在样本集T上的预测概率矩阵Pro(Sk,T) 如下
Pro(Sk,T)=p1,1p1,2…p1,c
p2,1p2,2…p2,c
pm,1pm,2…pm,c(25)
由于在随机森林算法中,输出的分类结果为投票结果最多的类别,即是预测概率最大的类别,所以采用argmax()函数对每个样本所有类别的概率值进行求参,获得每个样本最大概率对应的索引值,反映了子森林对该样本集中的每个样本的分类结果。组成的类别预测矩阵如下:
Pre(Sk,T)=arg max(p1,1p1,2…p1,c)arg max(p2,1p2,2…p2,c)
arg max(pm,1pm,2…pm,c)(26)
将矩阵Pre(Sk,T)与样本集T的实际类别矩阵C进行一一比对,其中分类正确的样本被标记为1,分类错误的被标记为0,由此可以获得层级预测矩阵:
LPM=[Pre(S1,T)==CT,Pre(S2,T)==CT,…,Pre(Sn,T)==CT](27)
证毕。
定理5 融合权重公式MWF。已知LPM为级联森林的层级预测矩阵,I0为输入样本的初始权重,则融合权重公式MWF*为
MWF*=limi→∞(LPMTIi-1BTnLPMTIi-1)(28)
其中: Ii=(Tmn-LPM)(Tnn-En)MWFiBTm(Tmn-LPM)(Tnn-En)MWFi(29)
I0=(Tmn-LPM)(Tnn-En)BnBTm(Tmn-LPM)(Tnn-En)Bn(30)
Tmn=11…111…1
11…1m×n(31)
En=10…001…0
00…1n×n(32)
Bn=111n×1(33)
证明 已知LPM为m×n层级预测矩阵,m为样本个数,n为子森林数目。在矩阵LPM中,对于每一个子森林,预测错误的样本被标记为0,预测正确的样本被标记为1。则每个样本的初始预测难度可以由式(34)表示。
(Tmn-LPM)(Tnn-En)Bn(34)
其值越大代表样本被越多的子森林预测错误,即更难以预测,反之则代表样本更容易预测。为了反映级联森林中输入样本的初始分类难易程度,可以对其进行单位范数的归一化,表示如下:
I0=(Tmn-LPM)(Tnn-En)BnBTm(Tmn-LPM)(Tnn-En)Bn(35)
其中值越大表明在級联森林层中样本更难预测,反之则更容易预测。而子森林的初始权重可以通过将层级预测矩阵中子森林分类正确的比重与样本的权重相结合而得到:
MWF1=LPMTI0BTnLPMTI0(36)
其分母同样为单位范数的归一化因子。接着对样本权重向量以及子森林权重向量分别进行迭代直至子森林权重收敛,样本的迭代权重向量和最终的子森林权重可以分别为
Ii-1=(Tmn-LPM)(Tnn-En)MWFi-1BTm(Tmn-LPM)(Tnn-En)MWFi-1(37)
MWF*=limi→∞(LPMTIi-1BTnLPMTIi-1)(38)
证毕。因此,通过融合权重公式MWF可以衡量样本分类难度和子森林的分类能力,赋予分类性能更好的子森林更大的权重。
2.3.3 森林构建
通过MWF公式对级联森林中的子森林进行权重赋予后,为进一步加快级联森林的构建效率,需要结合Spark模型对级联森林的每一级进行并行构建,具体过程如下:
a)首先对输入样本集进行bootstrap采样,再通过Spark中的RDD分区策略将采样后的数据集和OOB数据集分别划分为大小相同的数据块block,将其作为DATA_RDD数据集和OOB_RDD传输到worker节点中;
b)在worker节点上采用OOB_RDD数据集构建两个随机森林和两个完全随机森林,采用子森林分解策略对随机森林进行分解并赋予子森林相应的随机状态ri,采用mapToPair算子将子森林的编号与相应的随机状态进行合并形成键值对〈sfi,ri〉;
c)调用MapPartition算子在每个子森林上对OOB数据进行预测以获取每个子森林的权重值ωi,并采用mapToPair算子将子森林的编号与相应的权重值ωi进行合并形成键值对〈sfi,ωi〉;
d)调用MapPartition算子对executor节点中的子森林对样本进行预测并形成新的键值对〈IDi,Pi〉(IDi为样本id与子森林编号的组合数组,Pi为样本的类概率向量与子森林权重的组合数组),同时更新样本和每个子森林的权重值,并调用K折交叉验证函数以评估模型的预测准确率;
e)将节点中预测得到的键值对由master节点分配后传入相应的reducer节点合并,得到该层级联森林的预测概率类向量,如果K折交叉验证的结果显示模型预测准确率有所提升,则将类向量合并传入下一级级联森林进行训练,否则将类向量输出为最终的预测结果。
算法3 SFC-MW策略
输入:输入特征集α。
输出:分类概率向量Pre;该级级联森林模型以及下一级输入样本S。
a)森林分解
for级联层中的随机森林do
获取随机森林的随机状态
for随机森林Ri中的决策树do
获取决策树的随机状态
end for
将随机森林分解为p个子森林
end for
for子森林do
设置随机状态
end for
return子森林模型和相应的随机状态
b)权重分配
for子森林do
给予相同的权重
使用袋外数据训练子森林
计算层级预测矩阵LPM
通过融合权重公式MWF计算子森林的权重
将子森林的编号与权重进行合并形成键值对
end for
return分配权重后的子森林模型
c)森林构建
对特征集D进行bootstrap采样
将采样后的数据集划分为大小相同的数据块block
for数据块block do
输入至分配权重后的子森林进行训练
获得样本预测后的概率类向量
end for
对子森林模型进行K折交叉验证
if准确率提高
将预测的概率类向量与特征集D合并为数据集S
return概率类向量Pre
else
停止级联森林构建
return 数据集S
2.4 类向量合并
在对级联森林层输出的类向量结果进行合并时需要先等待各分布式节点上的模型训练终止。然而,由于Spark进行任务调度时遵循数据本地性优先的调度方式,而忽略了各个计算节点中构建的子森林的数量与负载情况,在合并时各节点结果时容易出现相互等待的现象,导致并行DF算法在类向量合并阶段会存在模型并行效率低的问题[20]。所以本文提出基于混合粒子群算法的负载均衡策略,通过对任务节点的负载分配进行智能寻优的方式提升模型的并行效率。其具体工作流程如下:
a)首先对所有任务节点的运行状态、健康情况和负载信息进行统计,获得各任务节点的负载状态。
b)将任务节点看做一群粒子P1,P2,…,Pm,初始化每个粒子的速度和位置,给定惯性权重ω、学习因子c1和c2以及初始退火温度T。
c)提出相应的适应度函数f(xi),计算每个粒子的适应度f(xi),并引入模拟退火算法中的Metropolis准则。
定理6 适应度函数FF。适应度函数的设计如下:
f(x)=1αLoad+βTasktime(39)
其中:Load为每個节点与理想负载之间的平均一阶范数;Tasktime为任务节点之间相互等待的最大时间;α和β为可调参数。
证明 假设节点的负载状态系数LCCi能够代表该节点的负载情况,LCC为所有任务分配至节点后实现负载均衡的期望值,LCCi-LCC则代表了每个节点与理想负载之间的差值,其平均一阶范数如下:
Load=1m‖LCCi-LCC‖1(40)
其大小反映的是每个任务节点负载情况与负载均衡期望值之间的偏差程度,即Load值越小偏差程度越小,反之越大。假设任务节点中最大任务完成时间为max(time),最小任务完成时间为min(time),二者之间的差值如下:
Tasktime=max(time)-min(time)(41)
其大小反映了任务节点之间相互等待的最大时间,Tasktime的值越小则节点之间相互等待的最大时间越小。故而,αLoad+βTasktime能够同时考虑节点任务负载的均衡以及节点的等待时间。由于适应度函数的取值趋向于最小值,所以对其取倒数可以获得:
f(x)=1α(1m‖LCCi-LCC‖1)+β(max(time)-min(time))=
1αLoad+βTasktime(42)
证毕。因此适应度函数f(x)能够衡量任务节点之间的均衡程度,从而使粒子朝着任务节点负载更为均衡的方向移动。
d)将xi粒子的适应度f(xi)其与pbesti,d进行比较,如果f(xi)>pbesti,d,则接受这个新位置xi,用该适应值替换当前的pbesti,d,否则判断概率p=exp(Δf/T)是否大于随机数rand(0,1),如果p=exp(Δf/T)> rand(0,1)也同样接受这个新位置xi,用该适应值替换当前的pbesti,d。对于全局极值gbestd和最优个体同样采用Metropolis准则进行更新。
e)适应值更新后依据速度和位置更新公式对粒子的速度和位置进行更新,当算法达到终止标准,即达到最大迭代次数或相邻两代偏差小于ΔP时输出全局最优位置,其对应的任务分配序列即为最优的分配方案,否则继续进行迭代计算。
f)各任务节点根据得到的任务分配方案进行任务分配,待各节点完成子森林训练后实行类向量合并,输出结果。
算法4 LB-HPSO策略
输入:任务数Ti(i=1,2,…m);任务节点数Ni及负载能力Li;负载状态Si(i=1,2,…n)。
输出:最优调度方案Pg=(pg1,pg2,…,pgN)。
初始化种群数量 n,惯性权重 ω,学习因子 c1、c2,退火温度 T和最大迭代次数 I
for k=1 to I do
for 粒子 xido
计算适应度函数 fitness(xi)
if fitness(xi)>pbesti
fitness(xi)→pbesti
else
if p=exp(Δf/T)>rand(0,1)
fitness(xi)→pbesti
end if
end if
end for
选择有最佳适应度的粒子作为pbesti
for 粒子xido
根据式(9)计算速度
根据式(10)更新粒子的位置
end for
输出最优调度方案Pg=(pg1,pg2,…,pgN)
2.5 PDF-MIMW算法时间复杂度分析
由于ForestLayer、BLB-gcForest、IPDFIT算法设计了优化策略来提高并行DF算法的性能,故选取它们与本文算法进行比较。本文算法的时间复杂度由特征降维、多粒度扫描、级联森林构建和负载均衡四部分组成,分别记为T1、T2、T3和T4。各部分具体时间复杂度计算如下:
a)特征降维阶段。该阶段的时间复杂度主要由特征划分、特征筛选和多粒度扫描三部分组成。假设特征划分后优势特征集P和候选特征集C的大小分别为s和c,则特征划分的时间复杂度为O(s+c+c log c)。假设特征过滤时从优势特征集和候选特征集中过滤的特征总数为d,则特征筛选的时间复杂度为O(s+c+m)。综上,特征提取阶段的时间复杂度T1为
T1=O(2s+2c+c·log c+d)(43)
b)多粒度扫描阶段。假设多粒度扫描的粒度为L,样本数量为n,森林中树的个数为N,则多粒度扫描的时间复杂度T2为
T2=O(N·n·d·L·log2(n·d))(44)
c)级联森林构建阶段。该阶段的时间复杂度主要由级联森林的构建和权重分配两部分组成。假设样本数量为n,森林中树的个数为N,特征数为d,级联森林层数为W,则级联森林构建的时间复杂度为O(PNm log2(n))。假设权重的迭代次数为I,则权重分配的时间复杂度为O(IN)。综上,级联森林构建阶段的时间复杂度T3为
T3=O(P·N·d·log2(n)+I·N)(45)
d)负载均衡阶段。该阶段的时间复杂度主要取决于LB-HPSO策略的时间复杂度。假设任务节点数为k,粒子群迭代次数为P,则负载均衡的时间复杂度T4为
T4=O(k·P)(46)
综上所述, PDF-MIMW算法的时间复杂度为
TPDF-MIMW=T1+T2+T3+T4(47)
ForestLayer算法在多粒度扫描阶段的时间复杂度为T1=O(NndL log2(nd))(其中n为样本数目,N为森林中树的个数,d为特征个数,L为多粒度扫描的粒度),在并行构建级联森林阶段的时间复杂度为T2=O(S·t+WFnd log2(n)/S)(其中 S为子森林的个数,t为随机森林中树的个数,W为级联森林层数,N为森林中树的个数,特征数为d),则ForestLayer算法的时间复杂度为
TForestLayer=O(NndL log2(nd)+S·t+WFnd log2(n)/S)(48)
BLB-gcForest算法在bag of little boostrap阶段的时间复杂度为T1=O(s·g/b+ny)(其中 n为样本数目,g为子样本集的大小,b为节点个数,y∈[0.5,1]),在多粒度扫描阶段的时间复杂度为T2=O(NndL log2(nd))(其中N为森林中树的个数,d为特征个数,L为多粒度扫描的粒度),在并行构建级联森林阶段的时间复杂度为T3=O(WFnd log2(n)/S)(其中 S为子森林的个数,W为级联森林层数,N为森林中树的个数,特征数为d),则BLB-gcForest算法的时间复杂度为
TBLB-gcForest=O(s·g/b+ny+NnoL log2(no)+WNnd log2 (n)/S)(49)
IPDFIT算法在特征降维时需计算每个特征的信息增益值,则该阶段的时间复杂度为T1=O(n·d/b+m3)(其中 n为样本数目,d为特征数,b为节点个数,选择后的特征数为m),在多粒度扫描阶段的时间复杂度为T2=O(NnoL log2 (no))(其中 o为特征降维后的特征个数,L为多粒度扫描的粒度),在并行构建级联森林阶段的时间复杂度为T3=O(2WFcno log2(n))(其中 W为级联森林层数,F为森林中树的个数,特征数为2co),则IPDFIT算法的时间复杂度为
TIPDFIT=O(n·d/b+m3+NnoL log2(no)+2WFcno log2(n))(50)
由于大数据环境下输入的数据量十分庞大,并且在深度森林模型中,其时间复杂度主要由输入至级联森林训练时的特征數量以及级联森林的层数所决定,即各算法时间复杂度中的d以及W。由于算法ForestLayer和BLB-gcForest并没有进行特征预处理,所以dPDF-MIMW< 3 实验结果及比较 3.1 实验环境 为验证本文PDF-MIMW算法可行性以及有效性,设计了相关实验进行分析。实验硬件配置为包括8个计算节点(1个主节点和7个从节点)主从结构的分布式集群。各计算节点的硬件配置均为Intel CoreTM i7-11700H CPU、16 GB DDR4 RAM、1 TB SSD,且各节点处于同一局域网内,并通过1 GB/s以太网进行通信。实验软件配置则统一安装Ubuntu 16.04.7、Apache Hadoop 2.7.7以及JDK 1.8.0的Java开发环境。集群中各计算节点的具体配置如表1所示。 3.2 实验数据 本文实验数据采用的四个数据集均为UCI数据库[21]的真实数据集,分别为YEAST、ADULT、IMDB以及SUSY。其中YEAST是一个预测蛋白质的细胞定位的酵母数据集;ADULT是从美国人口普查数据库中提取出的一个人口收入数据集;IMDB是一个对电影评论标注的文本分类数据集;SUSY是一个记录使用粒子加速器探测粒子的数据集。上述数据集的详细信息如表2所示。 3.3 評价指标 1)加速比 加速比是同一任务在单机计算系统和并行计算系统中运行时间的比值,可以有效衡量算法采用并行计算系统并行计算获得的时间性能提升效果,加速比定义如下: Sp=T1Tn(51) 其中:n为节点数目;T1为任务在单机中的运行时间;Tn为任务在具有n个节点的并行计算系统中的运行时间。Sp值越大说明任务在并行计算系统中获得的性能提升效果越好。 2)准确率 准确率(accuracy)是指分类模型正确分类的样本数与总样本数的比值,可以有效衡量算法的分类性能,准确率定义如下: accuracy=TP+TNTP+FN+FP+TN(52) 其中:TP、TN、FP、FN分別对应混淆矩阵中将正类样本预测为正类的样本数、将正类样本预测为负类的样本数、将负类样本预测为正类的样本数与将负类样本预测为正类的样本数。accuracy值越大代表该分类模型的分类效果越好。 3.4 算法可行性分析 为了验证PDF-MIMW算法在大数据环境下的可行性,本文采用表2中YEAST、ADULT、IMDB以及SUSY作为数据集,分别在并行节点数为1、2、4、6和8的Spark框架中,将算法在上述数据集中独立运行十次并取平均运行时间计算加速比。通过对算法在不同节点数下以及不同数据集的加速比进行分析,实现对PDF-MIMW算法的可行性分析。 PDF-MIMW算法在各数据集上的加速比如图5所示。从图5可以看出,随着节点数量的增加,PDF-MIMW算法在四个数据集上的加速比总体呈上升的趋势,并且随着数据集规模的逐步增长,PDF-MIMW算法加速比的上升趋势也愈加明显。其中,当节点数量为2时,PDF-MIMW算法在四个数据集上的加速比相差不大,分别比单节点增加了0.63、0.61、0.67、0.77;当节点数量为4时,算法在各数据集上的加速比相较于单节点分别增加了1.98、2.12、2.25、2.65;当节点数量为8时,PDF-MIMW算法在各数据集上的加速比相较于单节点有了显著提升,分别增加了3.69、3.83、4.12、4.81。产生这些结果的原因是:一方面PDF-MIMW算法提出了FE-FI策略,通过先划分后筛选的方式过滤了不相关和冗余特征,极大地提升了PDF-MIMW算法的并行化训练效率;另一方面PDF-MIMW算法在级联森林并行构建阶段提出了SFC-MW策略,该策略通过对级联森林进行细粒度并行化的方式提升了PDF-MIMW算法在大数据环境下的并行化训练效率。因此可得,在大规模数据集下,随着节点数量的增加,PDF-MIMW算法的并行化训练效率也会随之显著提升,这体现出PDF-MIMW算法适用于大规模数据集下的并行处理,同时也表明了PDF-MIMW算法在大数据环境下具有良好的可行性与有效性。 3.5 算法性能比较分析 3.5.1 算法分类效果 为评估PDF-MIMW算法的分类性能,采用accuracy作为评价指标,分别将PDF-MIMW、 ForestLayer、BLB-gcForest以及IPDFIT算法在四个数据集中进行对比实验,在实验中分别比较了上述算法的分类精确度accuracy,实验结果如图6所示。 由图6可知,在四个数据集中,PDF-MIMW算法的分类精确度始终高于ForestLayer、BLB-gcForest以及IPDFIT算法。在YEAST数据集中,相较于ForestLayer、BLB-gcForest以及IPDFIT算法,PDF-MIMW算法的分类准确率分别高出1.74%、1.27%和3.29%;在ADULT数据集中,相较于ForestLayer、BLB-gcForest以及IPDFIT算法,PDF-MIMW算法的分类准确率分别高出4.14%、2.97%和3.03%;在IMDB数据集中,相较于PDF-MIMW、ForestLayer、BLB-gcForest以及IPDFIT算法,PDF-MIMW算法的分类准确率分别高出3.52%、2.43%和5.24%;在SUSY数据集中,相较于ForestLayer、BLB-gcForest以及IPDFIT算法,PDF-MIMW算法的分类准确率分别高出7.22%、3.42%和5.52%。从上述数据可知PDF-MIMW在四个数据集中的分类精确度具有显著优势,在SUSY数据集中优势更为明显。造成这种结果的主要原因是 PDF-MIMW算法设计了SFC-MW策略,通过综合考量样本分类难度和子森林分类性能的方式,对分类能力强的子森林赋予更高的权重,从而提高了模型的分类性能。 3.5.2 算法运行时间 为验证PDF-MIMW算法的时间复杂度,本文将PDF-MIMW算法分别与ForestLayer、BLB-gcForest和IPDFIT算法在YEAST、ADULT、IMDB以及SUSY四个数据集上进行了五次对比实验,并取五次运行时间的均值作为最终的实验结果。实验结果如图7所示。 由图7可知,四个算法的运行时间都随着并行节点数的增加而下降,相比于ForestLayer、BLB-gcForest以及IPDFIT算法,PDF-MIMW算法在不同并行节点数不同数据集上消耗的运行时间较低,且随着并行节点数的增加PDF-MIMW算法的运行时间优势更为突出。其中,当处理数据量较小的数据集YEAST时,如图7(a)所示,节点数量为8的PDF-MIMW算法的运行时间分别比ForestLayer、BLB-gcForest和IPDFIT算法减少了15.85%、15.04%和11.24%;当处理数据量较大的数据集SUSY时,如图7(d)所示,节点数量为8的PDF-MIMW算法的运行时间分别比ForestLayer、BLB-gcForest和IPDFIT算法减少了24.78%、17.81%和14.68%。产生这种结果的主要原因是:a)PDF-MIMW算法采用了FE-FI策略,该策略消除了冗余特征在训练过程中的重复计算,降低了算法在冗余特征计算上的时间开销;b)PDF-MIMW算法通过LB-HPSO策略对每个节点的任务进行了合理分配,降低了算法由于节点之间相互等待而产生的时间开销。 3.5.3 算法加速比 為验证PDF-MIMW、ForestLayer、BLB-gcForest以及IPDFIT算法在大数据环境下的并行化性能,本文采用加速比作为评价指标,分析比较了PDF-MIMW在各个数据集上和其他三个算法的加速比差异,实验结果如图8所示。由图8可知,在处理YEAST、ADULT、IMDB和SUSY数据集时,各算法的加速比都随着节点数量的增加而逐渐上升,在节点数为8时加速比达到最大,并且随着数据规模的逐步扩大,PDF-MIMW算法在各数据集上加速比的上升趋势相较于其他三个算法更为显著。其中,在处理数据规模较小的数据集YEAST上,如图8(a)所示,各算法之间的加速比相差不大,当节点数量为2时,PDF-MIMW算法的加速比为1.68,分别比ForestLayer和BLB-gcForest算法的加速比低了0.06、0.12,比IPDFIT算法的加速比高了0.02;但当节点数量增加至8的时,PDF-MIMW算法的加速比却超过了其他四种算法,分别比 ForestLayer、BLB-gcForest和IPDFIT算法的加速比高出了0.30、0.17和0.25。在处理数据规模较大的数据集SUSY上,如图8(d)所示,PDF-MIMW算法的加速比始终高于其他三个算法,当节点数量为2时,PDF-MIMW算法的加速比为1.83,分别比ForestLayer、BLB-gcForest和IPDFIT算法的加速比高出了0.18、0.12和0.15;当节点数量为8时,PDF-MIMW算法的加速比为5.88,分别比ForestLayer、BLB-gcForest和IPDFIT算法的加速比高出了1.13、0.53和0.68。由数据分析可知,相较于ForestLayer、BLB-gcForest以及IPDFIT算法,PDF-MIMW算法有着更好的加速比性能,这主要有两方面原因:一方面是PDF-MIMW算法凭借SFC-MW策略对随机森林进行分解,充分利用了Spark平台的计算资源,提升了模型的并行性能,而且随着数据规模的扩大,PDF-MIMW算法通过高效的并行化子森林构建来降低算法总体运行时间的优势也被逐渐放大;另一方面是PDF-MIMW算法设计了LB-HPSO策略,该策略均衡了各节点之间的负载,提升了PDF-MIMW算法的加速比。所以PDF-MIMW算法有着更高的加速比,在节点数较多的情况下具有更高的并行效率。 4 结束语 针对大数据环境下并行DF算法的不足,本文提出了Spark下基于互信息和加权融合的并行DF算法PDF-MIMW。该算法首先提出基于互信息的特征提取策略FE-MI,结合特征重要性和冗余性度量对原始特征集进行筛选,过滤不相关和冗余特征;然后结合Spark框架提出了并行森林构建策略SFC-MW,通过并行构建加权的级联子森林以提升模型的训练效率和预测精度,提高了模型的分类性能;最后提出基于混合粒子群算法的负载均衡策略LB-HPSO,通过均衡集群中各节点之间的负载降低集群总体的平均反应时长,提升了类向量合并的效率。为验证PDF-MIMW算法性能,将PDF-MIMW与ForestLayer、BLB-gcForest以及IPDFIT算法,在数据集YEAST、ADULT、IMDB以及SUSY上进行比较验证。最终实验结果表明,本文算法能够大幅提升并行DF模型的训练效率。 尽管本文算法在大数据环境下有着相对较好的性能表现,但其仍存在一些不足:a)在数据量较少时,运行时间优势不突出;b)在不平衡数据集中,算法性能会受到较大限制。这些都是现阶段存在的不足,也将是未来的研究重点。 参考文献: [1]Zhou Zhihua,Feng Ji.Deep forest[J].National Science Review,2019,6(1):74-86. [2]Guan Jie,Guo Minkai,Fang Sen.Partial discharge pattern recognition of transformer based on deep forest algorithm[J].Journal of Phy-sics:Conference Series,2020,1437(1):012083. [3]Zheng Wenbo,Yan Lan,Gou Chao,et al.Fuzzy deep forest with deep contours feature for leaf cultivar classification[J].IEEE Trans on Fuzzy Systems,2022,30(12):5431-5444. [4]牛振东,石鹏飞,朱一凡,等.基于深度随机森林的商品类超短文本分类研究[J].北京理工大学学报,2021,41(12):1277-1285.(Niu Zhendong,Shi Pengfei,Zhu Yifan,et al.Research on classification of commodity ultra-short text based on deep random forest[J].Trans of Beijing Institute of Technology,2021,41(12):1277-1285.) [5]Qin Xiwen,Xu Dingxin,Dong Xiaogang,et al.The fault diagnosis of rolling bearing based on improved deep forest[J].Shock & Vibration,2021,2021(6):1-13. [6]Cheng Xuewei,Wang Sizheng,Zou Yi,et al.Deep survival forests with feature screening[J].Biomedical Signal Processing and Control,2023,79:104195. [7]Hu Bo,Wang Jinxi,Zhu Yifan,et al.Dynamic deep forest:an ensemble classification method for network intrusion detection[J].Electronics,2019,8(9):968. [8]Zaharia M,Chowdhury M,Franklin M J.Spark:cluster computing with working sets[C]//Proc of the 2nd USENIX Conference on Hot Topics in Cloud Computing.[S.l.]:USENIX Association,2010:10. [9]Zhu Guanghui,Hu Qiu,Gu Rong,et al.ForestLayer:efficient training of deep forests on distributed task-parallel platforms[J].Journal of Parallel & Distributed Computing,2019,132:113-126. [10]Chen Zexin,Wang Ting,Cai Haibin,et al.BLB-gcForest:a high-performance distributed deep forest with adaptive sub-forest splitting[J].IEEE Trans on Parallel and Distributed Systems,2021,33(11):3141-3152. [11]毛伊敏,耿俊豪,陳亮.结合信息论改进的并行深度森林算法[J].计算机工程与应用,2022,58(7):106-115.(Mao Yimin,Geng Junhao,Chen Liang.Improved parallel deep forest algorithm combining with information theory[J].Computer Engineering and Applications,2022,58(7):106-115.) [12]Kwon Y,Baek S K,Um J.Correlation between concurrence and mutual information[J].Journal of Statistical Mechanics:Theory and Experiment,2022,2022(9):093104. [13]Reena I,Karthik H S,Prabhu Tej J,et al.Local sum uncertainty relations for angular momentum operators of bipartite permutation symme-tric systems[J].Chinese Physics B,2022,31(6):163-169. [14]Meetu J,Vibha S,Narinder S,et al.An overview of variants and advancements of PSO algorithm[J].Applied Sciences,2022,12(17):8392. [15]Verikas A,Gelzinis A,Bacauskiene M.Mining data with random forests:a survey and results of new tests[J].Pattern Recognition,2011,44(2):330-349. [16]Lin Xiaohui,Li Chao Ren,Luo Weijie,et al.A new feature selection method based on symmetrical uncertainty and interaction gain[J].Computational Biology & Chemistry,2019,83:107149. [17]周博文,皋军,邵星.环状扫描的强深度森林[J].计算机工程与应用,2021,57(8):160-168.(Zhou Bowen,Gao Jun,Shao Xing.Strong deep forest with circular scanning[J].Computer Engineering and Applications,2021,57(8):160-168.) [18]Ma Pengfei,Wu Youxi,Li Yan,et al.DBC-forest:deep forest with binning confidence screening[J].Neurocomputing,2022,475:112-122. [19]Pang Ming,Ting K M,Zhao Peng,et al.Improving deep forest by screening[J].IEEE Trans on Knowledge and Data Engineering,2022,34(9):4298-4312. [20]Yin Linzi,Chen Ken,Jiang Zhaohui,et al.A fast parallel random forest algorithm based on spark[J].Applied Sciences,2023,13(10):6121. [21]National Science Foundation.UCI machine learning repository[EB/OL].(2023).https://archive.ics.uci.edu/.

