基于改进双树RRT*算法的冗余机械臂末端路径规划

吴剑雄 毕卓然 李宗道 李清都

收稿日期：2023-06-01；修回日期：2023-07-26  基金项目：国家自然科学基金资助项目（92048205）

作者简介：吴剑雄（1999—），男（回族），江苏镇江人，碩士研究生，主要研究方向为机械臂的运动控制；毕卓然（1996—），男，黑龙江哈尔滨人，硕士研究生，主要研究方向为机械臂末端结构设计；李宗道（1994—），男，河南郑州人，博士研究生，主要研究方向为冗余机械臂的双臂协作；李清都（1980—），男（通信作者），湖北襄阳人，教授，博士，主要研究方向为仿生机器人理论与技术、复杂系统的动力学与控制等（liqd@usst.edu.cn）.

摘  要：针对冗余机械臂的冗余特性与相关RRT*算法在规划机械臂末端路径的应用中存在的搜索效率较低、收敛性不稳定以及没有充分考虑到机械臂末端几何构型与自身运动特性对路径规划影响的问题，提出一种改进策略。首先，引入一种基于根尾节点连线夹角的采样点选择方式，并设置目标逼近区域。根据连续采样成功次数动态选择改进采样与随机采样。接着，将双树扩展策略与上述方法相结合。最后，将初始可行路径进行二次重连得到最终的优化路径。通过验证，改进双树RRT*方法能够有效地提升搜索效率、收敛性以及路径的优越性。虚拟碰撞体与胶囊碰撞体的引入也能较好地应对机械臂末端结构与运动特性带来的影响。使用Mujoco物理仿真引擎进行机械臂运动验证，证明该策略可以为冗余机械臂末端规划出一条较优的可行路径。

关键词：冗余机械臂；RRT*；末端路径；根尾节点；目标逼近区域；双树扩展；虚拟碰撞体；胶囊碰撞体；Mujoco

中图分类号：TP241    文献标志码：A

文章编号：1001-3695（2024）02-021-0459-07

doi：10.19734/j.issn.1001-3695.2023.06.0275

Redundant manipulator end-effector path planning based onimproved bidirectional RRT* algorithm

Wu Jianxionga，b，Bi Zhuorana，b ，Li Zongdaoa，b，Li Qingdua

（a.Institute of Machine Intelligence，b.School of Medical Instrument & Food Engineering，University of Shanghai for Science & Technology，Shanghai 200093，China）

Abstract：Aiming at the redundancy characteristics of the redundant manipulator and the relevant RRT* algorithm had issues with low search efficiency，unstable convergence and not fully considering the influence of the geometric configuration and self-motion characteristics of the redundant manipulators end effector on path planning in applications for planning the end-effector path，this paper proposed an improved strategy.Firstly，this paper introduced a sampling point selection method based on the angle between the root and end node connection，along with the establishment of a target proximity region.This method dynamically switched between improved sampling methods and random sampling methods based on the number of successful continuous samples.Subsequently，this paper combined the bidirectional tree expansion strategy with the aforementioned method.Finally，it reconnected the initial feasible path twice to obtain the optimized path.Through verification，it improved that the bidirectional tree RRT* method could effectively enhance search efficiency，convergence，and path optimality.The introduction of virtual collision bodies and capsule collision bodies could also effectively respond to the impact of the structure and motion characteristics of the end effector of the redundant manipulator.This paper used the Mujoco physics simulation engine to validate the movement of the redundant manipulator.This paper demonstrates that this strategy can plan a more optimal feasible end-effector path for the redundant manipulator.

Key words：redundant manipulator；RRT*；end-effector path；root and end node；target proximity region；bidirectional tree expansion；virtual collision bodies；capsule collision bodies；Mujoco

0  引言

在众多类型的机器人研究项目中，机械臂因其广泛的应用场景、较强的环境适应能力，成为该领域的研究热点。例如人形机器人、移动操作机器人以及一般的工业场景都有机械臂的身影。近年来，冗余机械臂因其灵活的操作性，也为机械臂的运动学算法提供了新的思路。

机械臂的末端路径规划算法一直是机械臂应用领域中的关键问题。常用的路径规划算法有D*算法以及A*算法。但是D*算法过于依赖初始路径的选择，且容易受到维度的惩罚。A*算法依赖于启发函数的选择且较难适应障碍物较多的场景。而RRT类算法凭借全局搜索性、对高维空间的兼容性以及较优的避障性能，更适合用于机械臂末端的路径规划。

代伟等人［1］引入基于sobol序列的采样点生成方式来代替传统随机采样，虽然采样点分布更均匀，但不利于在较为复杂的障碍物环境下搜索路径。周益邦等人［2］根据扩展节点至目标点的距离为代价对节点扩展进行取舍，并优化了重布线过程，改良了双向RRT*-Connect算法，在效率与生成的路径长度方面得到了提升，但在复杂环境下有可能会找不到路径。刘建宇等人［3］引入基于概率的目标偏置采样，结合前后采样点夹角约束提出了一种改进双向的RRT*方法，但是实验环境是基于二维地图的，没有拓展到三维空间。孙立新等人［4］提出了根据采样点距离树中最近节点的距离动态调节扩展步长，可以有效地降低节点的密集程度，但是该方法容易错过一些可行路径。Karaman等人［5］提出了在随机树扩展过程中加入重选父节点与重布线的过程，所得路径得到了明显优化，但是算法效率较低。Tahir等人［6］采用启发的方式生成树的扩展点。Klemm等人［7］提出了RRT*-Connect算法，结合了RRT*与RRT-Connect算法。Zhang等人［8］引入了节点自调节机制，减少了对搜索空间的无效搜索。Wang等人［9］提出了NC-RRT算法，该方法尽量缩小了采样空间，避免获得较为曲折的路线，但是缩小采样空间的同时限制了算法随机性，障碍物较多时易出现难以收敛的情况。

本文提出了一种根据连续采樣成功次数动态切换基于根尾节点连线夹角的采样点选择策略与随机采样策略的方法。该方式可以在障碍物密集的情况下，通过在采样区域的纯随机采样绕过障碍物，避免了局部收敛问题。在障碍物较少的情况下连续采样成功后，切换至基于根尾节点连线夹角的采样点，选择策略较快的靠近目标点，并设定目标点逼近区域，当有节点进入，将采样区域设置为逼近区域。采用起点与终点的双树扩展方式，每棵树按以上方式扩展，极大地提升了算法的收敛速度。对所得的初始路径进行二次重连，得到一条冗余节点较少的执行路径。在机械臂路径规划过程中，引入胶囊碰撞体与虚拟碰撞体，对机械臂末端路径进行合理约束。

1  冗余机械臂末端路径规划注意点

1.1  采样空间

移动机器人路径规划一般是基于二维平面的。相比之下，机械臂的末端路径是在三维空间中进行规划。应用于二维平面中的RRT类方法的采样点区域一般是选择能包络工作平面的矩形区域（每个节点与采样点用二维坐标（x，y）的形式给出）。应用于三维机械臂运动空间中的RRT类方法的采样点区域，是选择能包络工作空间的立方体区域（每个节点与采样点用三维坐标（x，y，z）的形式给出）。

1.2  针对冗余机械臂的路径规划

机械臂的路径规划分为机械臂末端与机械臂连杆的规划。对于非冗余机械臂，可以将机械臂连杆的规划与末端规划相结合，在算法扩展末端路径点时的障碍物判别条件中加入连杆的碰撞判断［4］，或是通过粒子群等优化算法直接搜索出一系列满足末端路径与连杆无碰撞的关节序列［10，11］。这些方式效率较低且会出现无法收敛的情况。冗余机械臂因其冗余度使其每一个末端位姿对应的机械臂构型有无数种，利用零空间无穷的性质在执行末端路径时，通过零空间自运动实现连杆避障［12］。这时将末端路径规划与连杆路径规划分离，要求末端路径生成算法的速度快、路径较优的收敛性好（不抑制算法随机性），以及能尽量避开奇异位置，且能在末端路径规划过程中考虑末端执行器与末端连杆几何构型的碰撞，从而减少连杆路径规划的碰撞检测计算过程。

1.3  虚拟碰撞体应对不可达与奇异末端位姿

当机械臂末端距离障碍物较近且靠近臂身时，算法为机械臂末端规划出的路径，有时会出现距离机械臂臂身过近，导致奇异位姿或超出其工作范围的情况［13］。在规划过程中，通过创建一个尺寸合适的虚拟障碍物，可以有效地引导路径在符合机械臂运动特性的范围内延伸。冗余机械臂的末端工作形状大致是环形区域，所以加入以机械臂基坐标系原点为底面圆心的圆柱碰撞体是较为适合的。如图1所示，如果按图1（a）所示的末端路径进行运动，机械臂极易出现奇异位姿或超出工作范围，从而导致规划失败。通过加入虚拟碰撞体，引导路径向更合理的方向扩展，提高规划成功率。

1.4  以路径线为轴心的胶囊状碰撞体包络末端

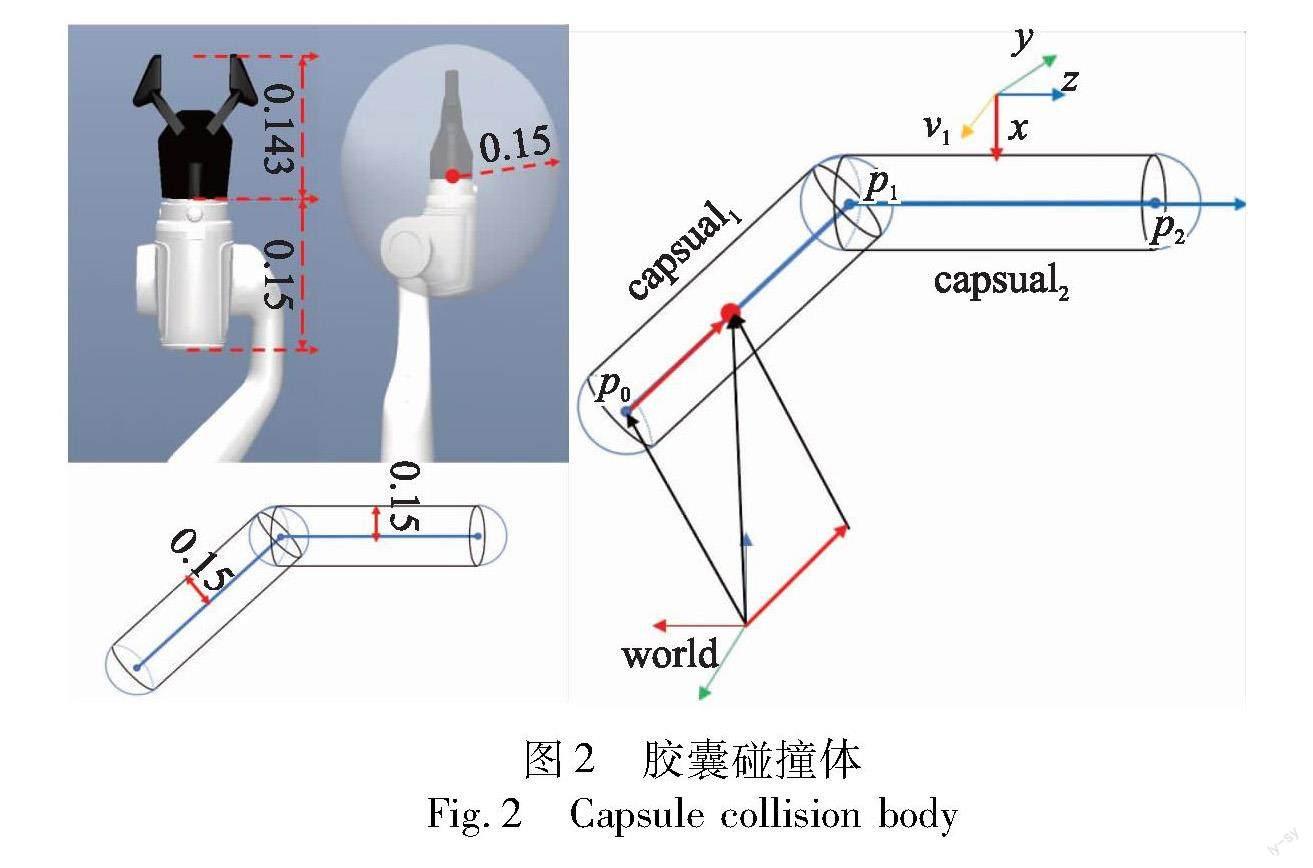
由算法得到的机械臂末端路径是机械臂末端坐标系原点的路径。末端在笛卡尔空间中的运动需要通过逆运动学分析将其映射到关节空间，并且机械臂末端规划还包含末端的姿态。这时，受机械臂末端连杆与末端执行器构型的影响，很有可能出现末端坐标系原点轨迹无碰撞，但是末端的几何结构与障碍物发生接触的问题。所以在规划机械臂末端路径时，光做直线与障碍物的碰撞检测是不够的，需要为路径直线也加上合适的碰撞体。本文选用以路径为轴的胶囊状碰撞体包络路径线。胶囊碰撞体能更好地契合路径的拐点，与路径线的拟合度较高。如图2所示，本文添加了长度为0.143的robotiq2f85型号末端夹爪，根据机械臂末端连杆长度为0.15，所以选择胶囊碰撞体的球半径为0.15。本文通过调用FCL库实现胶囊碰撞体与障碍物的碰撞检测，其中需要确定的是胶囊碰撞体的位姿问题。如图2（b）所示，在world坐标系中，表示capsual1中心位置需由式（1）计算。

capsual1_center=p0+（p1-p0）2（1）

由于胶囊由圆柱体与两个半球体组成，属于对称几何体，只需要保证其固连坐标系的z轴与路径线方向平行即可，x、y轴可通过向量叉乘的方式得到在world中的表达。以capsual2举例。

首先设置任意一个单位向量v1，并将z轴方向定义为路径线朝向且单位化。通过z轴与向量v1叉乘得到必垂直于z轴的向量，再对其单位化得到x轴。此时圆柱体坐标系的x、z轴相对于world的表达已得到，直接将z轴叉乘x轴即可得到y轴。将x、y、z进行列排即可得到对应的姿态变换矩阵。两个半球体可以膨胀为两个完整的球体与圆柱体，组合为胶囊体，只需将路径节点作为球体中心位置即可，无须考虑球体姿态。圆柱体在world中的姿态可以由式（2）算出，并作为参数传入FCL函数。

v1=［0，1，0］

z=p2-p1‖（p2-p1）‖

x=z×v1‖z×v1‖（x⊥z且x为单位向量）

y=z×x‖z×x‖（y⊥x⊥z且x、y、z均为单位向量）（2）

1.5  最后与终点的连线

RRT和RRT*算法最后到达终点的判断条件是，若节点至终点的欧氏距离小于一定范围，则直接相连。这个范围如果选择很小，则可能导致算法难以收敛，如果选择过大，则会出现最后的路径与障碍物发生碰撞的情况。通過将判断条件改为节点与终点是否能无碰撞连接作为算法结束条件，能避免上述问题。双树扩展也可以规避这个问题。

2  算法介绍

2.1  RRT*

RRT*算法是在基本RRT算法的基础上加入了重选父节点和重布线的过程。大致思路是先将路径起点作为搜索树上的根节点，在给定的搜索区域中随机选取一个采样点xrandom，并找到当前随机树上与采样点xrandom之间的欧氏距离最小的节点xnear，然后以xnear为起点，按一定的步长沿着xnear→xrandom方向延伸得到xextension，最后对xextension与xnear的连线进行碰撞检测，如果没有发生碰撞，则将xextension加入随机搜索树中，并设置xnear为xextension的父节点。搜索树中加入xextension后，以 xextension为中心按照一定范围找到与之邻近的节点集xnearSet，以路径代价为评判标准，分别对xextension和xnearSet重选父节点与重布线。具体流程如下：

a）将起点xinit加入搜索树。

b）在采样区域内随机选取一个采样点xrandom 。

c）在搜索树中找到与随机采样点之间欧氏距离最小的节点xnear。

d）按设定的步长以xnear为起点并沿着xnear→xrandom的方向进行扩展，得到扩展点xextension。

e）判断xextension与xnear的连线有没有触碰到障碍物。如果碰到障碍物则舍弃xextension并返回步骤b）。如果没有，则将xextension加入搜索树，并设置其父节点为xnear。

f）在以xextension为中心的给定范围内，找到目前搜索树上所有在这个范围内的节点形成xnearSet集合。分别计算存在于xnearSet的节点以及当前xnear回归至起点xinit的路径欧氏距离和，并分别加上xextension与xnearSet的各个节点和xnear之间的欧氏距离。找到欧氏距离和最小的节点xmin，将xextension的父节点重选为xmin，达到重选父节点的效果。

g）若xnear不是xmin，则在重布线过程中的xnearSet集合中不考虑xmin这个节点。分别将xnearSet中的其他节点与xextension之间的欧氏距离与xextension回归至起点xinit的欧氏距离和相加。如果该欧氏距离和小于对应xnearSet中的节点回归至起点xinit的欧氏距离和，那么将对应xnearSet中节点的父节点重新选为xextension，达到重布线的效果。

h）判断xextension与终点xend的欧氏距离。如果小于给定值，就直接连接xextension与xend，搜索结束；如果大于或等于给定值，则返回步骤b）继续扩展采样（本文将节点与终点是否能无碰撞连接作为算法结束条件）。

图3、4为重选父节点与重布线示意图，路径上的数字为节点间的欧氏距离。

2.2  改进双树RRT*算法

2.2.1  采样点的条件选择策略

一般将目标点按一定概率作为采样点的偏置采样策略，或者在目标区域内按目标点扩展的方式，在障碍物不密集的情况下效率的确有所提升，但是在障碍物较为密集的情况下，该方法极有可能导致局部极小的出现。

本文在搜索过程中定义一个累加器ACC并初始化为0。在随机树的扩展过程中先采用随机采样策略，当采样点扩展成功后，将累加器ACC进行累加。如果连续采样成功，则ACC也连续累加。直到一次采样不成功，直接将ACC重置为0。当ACC超过给定的阈值后，则代表目前区域的障碍物密集程度不高。这时就切换至根据采样点xrandom与xinit的连线和xinit与xend的连线角度选择采样点的生成方式，如式（3）所示。

SampleMethod=RandSampleACC≤β

ImporvedSampleACC>β（3）

范围偏置采样如图5所示（三角为采样点）。

如图5（a），当采样点在区域外时，直接设xend为采样点进行扩展。如图5（b），当采样点在区域（二维空间中为扇形，三维空间中区域为圆锥）内时，则按原采样点扩展。该方式可以让随机树偏向目标点扩展的同时减小目标点的偏置影响，增加随机树扩展的可能性。在障碍物较多与较少的情况下均有不错的适应性。如图5（c），随机树起点处的一个较大障碍物导致刚开始扩展时的成功率较低，累加器会低于阈值。此时采用随机采样绕过障碍物后，障碍物较为稀疏，采样成功率提高，此时会切换至上述非随机采样策略向目标点靠近，如式（4）（5）所示。

θ=arcos（（xend-xinit）·（xrand-xinit）‖（xend-xinit）‖·‖（xrand-xinit）‖）（4）

xrandom=xrandθ≤α

xendθ>α（5）

目标区域采样如图6所示（三角为采样点。虚线框为以xend为中心的逼近区域）。在随机树扩展的初期，xrandom在给定区域中随机选取。以xend为中心，构建一个逼近区域。当最新的xextension进入了该区域，则之后的xrandom均在这个逼近区域内选取，在逼近区域中，扇形或圆锥体区域占比更高，从而可以引导路径以更快且不失随机性的特性到达xend。如图所示，当框内左上角有节点扩展进入时，采样区域将被缩小至该区域内，并继续按上文的采样策略采样。

改进采样后的单树扩展算法可以表示为如下伪代码形式：

由于RRT*算法的重选父节点与重布线过程需要计算节点回归至起点的欧氏距离和。本文将节点封装为第二行的结构体形式，每次扩展后更新当前节点的三维位置、父节点在树中的索引以及当前节点与其父节点的欧氏距离。在重选父节点以及重布线过程中动态更新当前节点与范围内节点的结构体数据。在回归过程中只需进行加和运算即可，无须重复进行开根运算，提升算法速度。

1  ACC←0；α←value1；β←value2；O2S←xend-xinit；dstep=value3；isclose=0；

2  Tree={}；Tree.add（xinit，distance，father）；

//節点树结构体（三维位置，与父节点欧氏距离，父节点编号）

3  while（1）

4  if isclose==0

5    xrandom=rand（GobalArea）；

6  else

7    xrandom=rand（NearArea）；

8  if ACC>β：

9    if arcosO2S·（xrandom -xinit ）‖O2S‖·‖（xrandom-xinit）‖ > α

11      xrandom=xend

12  find min（‖（xrandom-xi）‖）（xi∈Tree.x）；xnear=xi；xextension=xnear+（xrandom-xnear）·dstep

13  if collision（line（xextension-xnear），collisionobj）==false

14    ACC←ACC+1；Tree.add（xextension，distance（xextension，xnear），xnearID in Tree）；

15    Repet_Select_Father（xextension，Tree）；

//在重布线与重选父节点函数中

16    Repet_Select_Line（xextension，Tree）；

//根据重连结果更新相应节点的distance与father

17    if （xextension in NearArea and isclose==0）

18      isclose=1；

19    if（collision（line（xextension-xend），collisionobj）==false）

20    break；

21  else

22    ACC←0；

23  end

2.2.2  双树扩展

分别定义起点为xinit与xend的两棵随机树Tree1、Tree2，并定义一个切换变量switch。Tree1以xend为终点，Tree2则以xinit为终点。先对Tree1中的节点进行扩展，如果发生碰撞，则重新尝试扩展，直到扩展成功后就取反switch切换至Tree2进行扩展。当Tree1和Tree2最新扩展的节点能无碰撞联通后，就获得了一条初始可行路径，如图7所示（三角为Tree1的采样点，五角为Tree2的采样点）。

2.2.3  二次重连

该过程是在算法得到一条可行路径后，对路径的二次优化。将获得的可行路径节点存入Road1，并将Road1的第一个节点存入空路径Road2中，定义两个指针（pointinit、pointend）分别指向Road1的第一个节点与最后一个节点，判断pointinit指向的节点与pointend指向的节点之间是否可以无碰撞联通。若是，则将pointend当前指向的节点加入空树Road2，接着将pointinit指向pointend所指向的节点。若发生碰撞，则将pointend指向当前指向节点的上一节点继续碰撞检测，直到pointend指向了pointinit当前指向节点的下一个节点。如此往复，当pointinit指向了Road1的最后一个节点时，得到二次重连后的路径Road2，如图8所示。将得到的初始可行路径重连后得到了一条更优越的路径。

2.2.4  结合后的改进双树RRT*算法

将2.2.1～2.2.3节的方法结合至RRT*方法后的三维空间路径搜索，具体伪代码如下所示。

1  ACC1←0；ACC2←0；α←value1；β←value2；switch←1；

2  O2S←xend-xinit；dstep=value3；isclose1=0；isclose2=0；

3  Tree={}；TreeS={}；TreeE={}；

4  TreeS.add（xinit，distance，father）；TreeE.add（xend，distance，father）；

5  while（1）

6    if switch==1：

7    if isclose1==0：

8      xrandom=rand（GobalArea）；

9    else

10      xrandom=rand（NearArea1）；

11    Tree=TreeS；

12    if ACC1>β

13      if arcos（O2S·（xrandom -xinit ）‖O2S‖·‖（xrandom -xinit ）‖）>α

14        xrandom=xend

15  else

16    if isclose2==0：

17      xrandom=rand（GobalArea）；

18    else

19      xrandom=rand（NearArea1）；

20    Tree=TreeE；

21    if ACC2>β

22    if arcos（-O2S·（xrandom -xend ）‖-O2S‖·‖（xrandom -xend ）‖） > α

23    xrandom=xinit

24  find min（‖（xrandom-xi）‖）（xi∈Tree.x）；xnear=xi；xextension=xnear+（xrandom-xnear）·dstep

25  if collision（line（xextension-xnear），collisionobj）==false：

26    if switch==1：ACC1←ACC1+1；else：ACC2←ACC2+1；

27    Tree.add（xextension，distance（xextension，xnear），xnear ID in Tree）；

28    Repet_Select_Father（xextension，Tree）；

//在重布線与重选父节点函数中

29    Repet_Select_Line（xextension，Tree）；

//根据重连结果更新相应节点的distance与father

30    if switch==1：if （xextension in NearArea1 and isclose1==0）：isclose1=1；

31    else

if（xextension in NearArea2 and isclose2==0）：isclose2=1；

32    switch=-switch

33    if（collision（line（TreeE.xextension-TreeS.xextension）， collisionobj）==false）

34      break；

35  else

36    if switch==1：ACC1←0；else：ACC2←0；

37  SecondaryReconnection（PathSplicing（TreeS，TreeE））；

38  end

3  改进算法对比实验

对比实验部分基于ubuntu20.04版本的Python3.8.10环境，算法对比实验部分的球形碰撞检测算法实现参考文献［11］。

3.1  改进采样策略的有效性

为验证改进采样策略在随机树搜索过程中是否有效，设置采样步长为0.1，θ设为π/12，起始点为［200 -50 300］，目标点为［200 2000 700］，累加器阈值设为5，逼近区域设置为以随机树终点为中心的半边长为200 mm的正方体区域。如图9（三角为在夹角小于θ的区域内的采样点，红色虚线为采样扩展延长线，绿点为树中的非路径点，参见电子版）所示，起点处障碍物较密集，这时算法主要以采样空间随机采样为主。待越过障碍物后，采样成功率提高，累加器超过阈值后，便开始向目标点或三角采样点扩展。待再次遇到障碍物后，继续随机采样，越过障碍物后与目标点无障碍连通。

3.2  加入改进采样策略的单树RRT*法与其他算法对比

RRT*为方法1，按0.5的概率直接将目标点偏置为采样点的RRT*算法为方法2，RRT*-connect算法［7］为方法3，改进双向RRT*-connect算法［2］为方法4，改进双向RRT*-connect算法［3］为方法5，加入改进采样的RRT*算法为方法6。采样空间为0≤x≤600，-200≤y≤700，0≤z≤650的立方体。扩展步长均设置为0.3。重布线与重选父节点的区域为以xextension为球心，半径为800 mm的球体。累加器给定阈值为5。θ设为π/8。逼近区域设置为以随机树终点为中心的棱长为200 mm的正方体。场景中共有19个半径为100 mm的球形障碍物。路径起点为［0 0 0］，终点为［350 700 700］。运用这三种方法分别搜索100条可行路径。表1为方法1～6的对比。图10为各方法的路径与采样点分布图。可以看出，加入改进采样方式的单树RRT*方法在采样点个数、搜索时间以及路径长度上表现良好。

3.3  改进双树RRT*法

改进双树RRT*算法为方法7，运用改进双树RRT*算法在相同的条件下获取100组可行路径。其与方法1～6的对比如表2所示（其中绿色三角为扩展Tree1的采样点，蓝色五角为扩展Tree2的采样点，参见电子版）。表2为方法1～7的对比。图11为方法7获取的一组路径与采样点分布图（黑色节点为初始可行路径的冗余节点，绿色细线为冗余路径）。可以看出，加入双树扩展与二次重连之后的改进法在采样点个数、搜索时间以及路径长度上有更好的表现。

4  Diana7 Med机械臂末端运动仿真

Diana7 Med是一款由思灵公司自主研发的具有关节偏置的高性能七自由度冗余机械臂。仿真环境基于ubuntu20.04版本的Python3.8.10、ros-noetic、python-fcl、orocos-kdl 1.5.0、PyKDL、mujoco2.3.1。

4.1  机械臂运动学分析

由于该机械臂关节与关节之间存在相对于x、y轴的偏置较多，故采用DH参数法建模会导致构建的末端坐标系与机械臂实际末端有偏差，所以本文通过将该机械臂的URDF文件导入至KDL库建立运动链，完成对机械臂的运动学建模。将URDF文件导入至rviz可视化后，如图12所示。

在实验中运用了KDL库作逆运动学解算，以及笛卡尔空间中的直线位置插值。Mujoco环境中的机械臂位置控制采用PD控制器，输入关节位置，输出关节扭矩。由于欧拉角插值会发生突变［14］，轴角插值过程中轴具有不可控性［15］，所以实验中选用了四元数球面插值法进行姿态的平滑插值。如式（6）所示，其中t∈［0，1］，θ=arcos（p·q），p为初始姿态的单位四元数表达，q为目标姿态的单位四元数表达。通过离散t进行姿态插值。

Slerp（p，q，t）=sin［（1-t）θ］p+sin（tθ）q

sin θ（6）

4.2  实验场景构建

在实验中共选用了两个球形障碍物与五个圆柱体障碍物（其中有一个为1.3节所述的虚拟障碍物）。

Mujoco中的仿真环境如图13所示，其中夹爪型号为robotiq2f85。虚拟碰撞体为半高0.6 m、底面半径为0.3 m的圆柱体。

4.3  机械臂末端路径规划

规划过程中在碰撞检测环节为路径添加胶囊状碰撞体，其胶囊高度为路径长度，两端球半径为0.15 m。碰撞体检测环节调用FCL碰撞检测包的多碰撞检测接口实现。采样空间为0≤x≤0.6，-0.68≤y≤0.6，0.15≤z≤1.13的立方体空间。累加器给定阈值5，扩展步长为0.8，θ设置为π/10。逼近区域设置是以终点为中心的棱长为0.2 m的正方体。起点为［0.3698 -0.5987 0.1298］，终点为［-0.0827 0.7892 0.3678］。姿态由四元数来表示，起始姿态为［-0.1546 -0.2748 -0.4653 0.8271］，目标姿态为［0.2959 -0.2677 0.6800 0.6152］。规划出的路径如图14所示。

基于Mujoco环境下的机械臂运动仿真路径如图15所示，可以看出，机械臂末端按图14规划出的路径进行末端运动。

5  结束语

考虑到冗余机械臂相比于非冗余机械臂有着零空间无穷的特性，使得其可以通过灵活的零空间自运动［11］进行连杆避障，从而使得末端路径规划与连杆路径规划分离。本文基于RRT*算法，结合基于根尾节点连线夹角的采样方式，目标逼近区域的设置，双树扩展的机制以及可行路径的后处理提出了一种改进双树RRT*方法。经实验证明，该方法在采样点个数、搜索时间与所得路径长度上相比于相关改进算法有不错的表现。

通过为末端执行器与末端連杆加入胶囊包络体，可以使得冗余机械臂在末端路径规划过程中处理掉一部分碰撞体，从而减少连杆在零空间中避障时的碰撞检测环节，且能得到相对更安全的末端路径。根据场景与机械臂自身运动特性构建合适的虚拟碰撞体，可以使路径向更符合机械臂运动特性的方向延伸。

下一步將为该算法获得的末端路径加入基于样条插值的平滑处理，并结合相关获取冗余机械臂零空间的方法（如几何臂角法、QP迭代法等）形成一整套机械臂运动避障策略。算法调试稳定后，将迁移至结合三维激光雷达与实物机械臂的实物平台进行进一步验证。

参考文献：

［1］代伟，李创业，杨春雨，等.基于低差异序列与快速扩展随机树融合算法的机械臂路径规划［J］.控制理论与应用，2022，39（1）：130-144.（Dai Wei，Li Chuangye，Yang Chunyu，et al.Robot arm path planning based on low difference sequence and fast extended random tree fusion algorithm［J］.Control Theory and Application，2022，39（1）：130-144.）

［2］周益邦，章兰珠，徐海铭.基于改进双向RRT～*算法的机械臂路径规划［J］.计算机应用，2022，42（S1）：342-346.（Zhou Yibang，Zhang Lanzhu，Xu Haiming.Robot arm path planning based on improved bidirectional RRT～* algorithm［J］.Journal of Computer Applications，2022，42（S1）：342-346.）

［3］刘建宇，范平清.基于改进的RRT～*-Connect算法机械臂路径规划［J］.计算机工程与应用，2021，57（6）：274-278.（Liu Jianyu，Fan Pingqing.Robot arm path planning based on improved RRT～*-connect algorithm［J］.Computer Engineering and Applications，2021，57（6）：274-278.）

［4］孙立新，高建明，高春艳，等.基于改进RRT*算法的七自由度机械臂避障路径规划［J］.控制工程，2023，30（9）：1592-1597，1615.（Sun Lixin，Gao Jianming，Gao Chunyan，et al.Obstacle avoidance path planning of seven-degree-of-freedom manipulator based on improved RRT* algorithm［J］.Control Engineering，2023，30（9）：1592-1597，1615.）

［5］Karaman S ，Frazzoli E .Sampling-based algorithms for optimal motion planning［J］.The International Journal of Robotics Research，2011，30（7）：846-894.

［6］Tahir Z，Qureshi A H，Ayaz Y，et al.Potentially guided bidirectionalized RRT* for fast optimal path planning in cluttered environments［J］.Robotics and Autonomous Systems，2018，108：13-27.

［7］Klemm S，Oberlnder J，Hermann A，et al.RRT*-Connect：faster，asymptotically optimal motion planning［C］//Proc of IEEE International Conference on Robotics and Biomimetics.Piscataway，NJ：IEEE Press，2015：1670-1677.

［8］Zhang Haojian，Wang Yunkuan，Zheng Jun，et al.Path planning of industrial robot based on improved RRT algorithm in complex environments［J］.IEEE Access，2018，6：53296-53306.

［9］Wang Xinda，Luo Xiao，Han Baoling，et al.Collision-free path planning method for robots based on an improved rapidly-exploring random tree algorithm［J］.Applied Sciences，2020，10（4）：1381.

［10］雷超帆.基于改进蚁群算法的六自由度机械臂避障路径规划［D］.郑州：郑州大学，2019.（Lei Chaofan.Obstacle avoidance path planning of six-degree-of-freedom manipulator based on improved ant colony algorithm［D］.Zhengzhou：Zhengzhou University，2019.）

［11］朱战霞，靖飒，仲剑飞，等.基于碰撞检测的空间冗余机械臂避障路径规划［J］.西北工业大学学报，2020，38（1）：183-190.（Zhu Zhanxia，Jing Sa，Zhong Jianfei，et al.Obstacle avoidance path planning of space redundant manipulator based on collision detection［J］.Journal of Northwest Polytechnical University，2020，38（1）：183-190.）

［12］周送鋼.基于零空间自运动的七轴冗余机械臂避障算法研究［D］.合肥：合肥工业大学，2022.（Zhou Songgang.Research on obstacle avoidance algorithm of seven-axis redundant manipulator based on zero-space self-motion［D］.Hefei：Hefei University of Technology，2022.）

［13］史士财，尹斌，蒋再男.一种七自由度冗余机械臂的奇异构形特征分析［J］.机械与电子，2014（10）：67-70.（Shi Shicai，Yin Bin，Jiang Zainan.Singular configuration analysis of a seven-degree-of-freedom redundant manipulator［J］.Mechanical and Electronics，2014（10）：67-70.）

［14］普亚松，张文斌，蔺小军，等.Hopf映射在机械臂四元数姿态规划中的应用研究［J］.机电工程，2020，37（11）：1387-1392.（Pu Yasong，Zhang Wenbin，Lin Xiaojun，et al.Application of Hopf mapping in quaternion attitude planning of manipulator［J］.Electromechanical Engineering，2020，37（11）：1387-1392.）

［15］孙斌，常晓明，段晋军.基于四元数的机械臂平滑姿态规划与仿真［J］.机械科学与技术，2015，34（1）：56-59.（Sun Bin，Chang Xiaoming，Duan Jinjun.Smooth attitude planning and simulation of manipulator based on quaternion［J］.Mechanical Science and Technology，2015，34（1）：56-59.）

［16］张兰勇，韩宇.基于改进的RRT*算法的AUV集群路径规划［J］.中国舰船研究，2023，18（1）：43-51.（Zhang Lanyong，Han Yu.AUV swarm path planning based on improved RRT* algorithm［J］.China Ship Research，2023，18（1）：43-51.）

［17］王红莉，向国菲，朱雨琪，等.基于PS-RRT算法的机械臂避障路径规划［J］.计算机应用研究，2023，40（1）：42-46.（Wang Hongli，Xiang Guofei，Zhu Yuqi，et al.Obstacle avoidance path planning of manipulator based on PS-RRT algorithm［J］.Application Research of Computers，2023，40（1）：42-46.）

［18］张建冬，王东，马立东，等.基于改进RRT算法的移动机械臂路径规划［J］.电子测量技术，2021，44（23）：48-53.（Zhang Jiandong，Wang Dong，Ma Lidong，et al.Mobile manipulator path planning based on improved RRT algorithm［J］.Electronic Measurement Techno-logy，2021，44（23）：48-53.）

［19］贾焦予，袁杰，李中华，等.葡萄采摘机器人终端作业路径规划方法研究［J］.计算机工程与应用，2023，59（14）：285-292.（Jia Jiaoyu，Yuan Jie，Li Zhonghua，et al.Research on terminal operation path planning method of grape picking robot［J］.Computer Engineering and Application，2023，59（14）：285-292.）

［20］张一帆，史国友，徐家晨.基于人工势场法引导的Bi-RRT的水面无人艇路径规划算法［J］.上海海事大学学报，2022，43（4）：16-22.（Zhang Yifan，Shi Guoyou，Xu Jiachen.An unmanned surface vehicle path planning algorithm based on Bi-RRT guided by artificial potential field method［J］.Journal of Shanghai Maritime University，2022，43（4）：16-22.）

［21］Sun Yuxi，Zhang Chengrui，Sun Pengcheng，et al.Safe and smooth motion planning for mecanum wheeled robot using improved RRT and cubic spline［J］.Arabian Journal for Science and Engineering，2020，45（4）：3075-3090.

［22］Gammell J D，Srinivasa S S，Barfoot T D.Informed RRT*：optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic［C］//Proc of IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway，NJ：IEEE Press，2014：2997-3004.