基于金枪鱼群算法优化极限学习机的混凝土抗压强度预测

张博吾 耿秀丽

收稿日期：2023-05-22；修回日期：2023-07-28  基金項目：国家自然科学基金面上项目（72271164）；教育部人文社会科学研究规划基金资助项目（19YJA630021）

作者简介：张博吾（1999—），男，山西晋城人，硕士研究生，主要研究方向为机器学习；耿秀丽（1984—），女（通信作者），山东东营人，教授，博士，主要研究方向为产品服务系统、服务科学、决策理论与方法等（xlgeng@usst.edu.cn）.

摘  要：混凝土抗压强度是建筑结构设计与评价的一个重要指标，它直接关乎建筑的质量与安全。为解决现有机器学习模型对其预测存在预测耗时长、精度不够高，不能很好地满足施工现场对混凝土抗压强度预测实时性与准确性要求的问题，提出一套基于新式仿生算法金枪鱼群算法优化极限学习机（TSO-ELM）的混凝土抗压强度预测方法。该方法通过对ELM隐藏层初始参数中的连接权值与偏置值使用TSO进行寻优，有效提升了ELM的预测准确度。在仿真实验部分，通过两组混凝土数据集对ELM的预测速度、TSO的寻优能力、TSO-ELM模型的泛化性逐一进行验证。结果表明，该方法可以有效提高预测的速度与精准度，迭代次数更少，同时具有良好的泛化性，为现场施工及时进行混凝土抗压强度的预测提供了一种新方法。

关键词：混凝土；抗压强度；金枪鱼群优化算法；极限学习机；软测量

中图分类号：TP18    文献标志码：A

文章编号：1001-3695（2024）02-019-0444-06

doi：10.19734/j.issn.1001-3695.2023.05.0237

Prediction of concrete compressive strength based on tuna swarm algorithm

optimization extreme learning machine

Zhang Bowu1，Geng Xiuli1，2

（1.Business School，University of Shanghai for Science of Technology，Shanghai 200093，China；2.School of Intelligent Emergency Management，University of Shanghai for Science of Technology，Shanghai 200093，China）

Abstract：The compressive strength of concrete is a crucial parameter in the design and evaluation of building structures，as it directly impacts the quality and safety of buildings.To solve the current problem that the prediction of concrete compressive strength by the existing machine learning models suffers from issues such as long prediction times and low precision，which cannot meet the real-time and accuracy requirements of the prediction on construction sites，this paper proposed a novel method for predicting concrete compressive strength based on the tuna swarm optimization algorithm（TSO-ELM）.The proposed method utilized TSO to optimize the offset value of the connection weight in the initial parameters of the ELM hidden layer，thereby enhancing the prediction accuracy of ELM.In the simulation experiment，it verified the prediction speed of ELM，the optimization ability of TSO，and the generalization of the TSO-ELM model using two sets of concrete data.The results demonstrate that the proposed method can significantly improve prediction speed and accuracy with fewer iterations and better generalization，providing a new approach for the timely prediction of concrete compressive strength in field construction.

Key words：concrete；compressive strength；tuna swarm optimization；extreme learning machine；soft sensor

0  引言

混凝土作为最常用的建筑材料之一，被广泛地应用于各种工程建设中，混凝土抗压强度是其结构设计与性能评价的重要指标，并且直接关系到混凝土结构的安全。传统的混凝土抗压强度检测办法是先对混凝土试件进行28天标准养护后再测试。在实际施工过程中，为了保障质量安全，需要不断调整、适配实验，这会浪费很多原材料，费时费力，并且难以获得较为准确的结果，导致对工期和施工质量有一定影响。因此，如果能够对混凝土试块的抗压强度进行精准而快速的现场预测，将对实际工程帮助巨大，具有重要的研究意义。

近年来，随着计算机技术的飞速发展，机器学习理论与方法已被广泛应用于解决工程应用和科学领域的复杂问题。在使用机器学习算法对混凝土强度进行预测方面，近年来众多学者也开展了大量研究工作，取得了许多成果。陈洪根等人［1］建立了一套基于BP神经网络的粉煤灰混凝土抗压强度预测模型，为粉煤灰混凝土强度的相关分析提供参考和指导；韩建军等人［2］通过分析垃圾飞灰不同掺量对高性能混凝土抗压强度的影响，建立了一套基于BP神经网络的垃圾飞灰混凝土抗压强度预测模型；郭耀东等人［3］以再生粗骨料取代率、水灰比与混凝土表观密度三个指标为影响因素，建立了一套基于BP神经网络的再生保温混凝土抗压强度预测模型。在用于混凝土抗压强度预测方面，BP神经网络的优点是预测精准度较高，然而因为其需要不断反向地去计算调整各个层间的权值和阈值，导致学习速度缓慢，不能很好地满足生产中快速获得混凝土预期抗压强度以即时修正拌和料这一需求；同时BP神经网络还存在易出现过度训练导致模型泛化性能下降的问题。

针对BP神经网络的这些缺点，有学者使用了其他的机器学习算法进行预测。曹斐等人［4］以支持向量回归（support vector regression，SVR）为理论基础，建立了一种基于马氏距离的加权型SVR（MWSVR）的混凝土抗压强度预测模型；李杨等人［5］提出了一种基于CART决策树算法优化SVR回归算法的混凝土抗压强度预测方法。然而SVR的核函数参数、规则化系数等设置较为复杂，且其核函数必须满足Mercer条件；此外在处理高维度或大样本的数据时，SVR表现较差，预测精度不够高。

极限学习机（extreme learning machine，ELM）的输入层与隐藏层的连接权值、隱藏层的阈值可以随机设定，并在学习过程中保持固定，不用再调整，可以减少计算量。同时ELM的隐藏层和输出层之间的连接权值不需要迭代调整，而是以解方程组的方式一次性确定。通过这样的规则，基于极限学习机的模型泛化性能很好，学习速度有所提高。自从极限学习机问世以来，在诸多领域得到了广泛应用。冯禹铭等人［6］构建了基于粒子群算法优化极限学习机（PSO-ELM）的机器人精度补偿办法，提高了工业机器人在实际运用中的绝对定位精度；盛晓晨等人［7］建立了基于改进粒子群优化极限学习机的软测量建模方法，并以脱丁烷塔过程进行仿真实验，结果表明其方法有良好的精度与泛化性能。同样，在混凝土抗压强度预测方面，也有学者建立基于ELM的混凝土抗压强度预测模型。Abobakr等人［8］建立了一套基于极限学习机的混凝土抗压强度预测模型，并将预测结果与BP神经网络预测的结果进行比较，预测精度相似，但ELM的速度更快；严东等人［9］建立了一套基于特征提取和ELM的软测量方法，并将其应用于混凝土抗压强度预测中，取得了很好的效果。研究表明，虽然极限学习机在大部分情况下可以获得良好的性能，但隐藏层初始参数（连接权值偏置值、隐藏层的节点个数）对极限学习机分类精度仍存在很大影响，不恰当的参数会导致比较差的回归结果，进而影响模型的泛化性能。但是超参数的设定是一个黑盒问题，无法通过具体的计算得出，只能依靠经验手动设置。因此吴小平等人［10］提出了一套基于贝叶斯优化极限学习机（BOA-ELM）的混凝土抗压强度预测方法，但其模型平均训练时间较长，泛化性能表现一般。近年来仿生智能算法发展迅速，适合用于解决复杂优化问题。金枪鱼群优化算法（tuna swarm optimization，TSO）的灵感来源于金枪鱼群的两种种群体觅食行为，具有调整参数少、计算简单等优点。自问世以来，已经有学者在其他领域使用TSO对原有方法进行优化，取得了一些成效。薛萍等人［11］使用金枪鱼群优化算法对原有的作物分生育阶段产量-耗水量关系模型进行优化，结果表明运用了TSO的新模型拟合精度高且寻优速度快，取得了更佳的效果；赵力等人［12］将二进制金枪鱼群优化算法用于求解满足测试性指标和故障可诊断性水平的最优测试集合，取得了良好的效果。

本文提出了一种基于金枪鱼群算法优化极限学习机的混凝土抗压强度预测模型。运用金枪鱼群优化算法对极限学习机的输入超参数进行快速寻优，以提高其预测精度。使用两个数据集分别对此模型的预测效率、精准度与泛化性能进行测试。经过实验验证与结果对比，验证了提出的基于金枪鱼群算法优化极限学习机的混凝土抗压强度预测模型在混凝土抗压强度预测中具有较快的速度与较高的精准度，同时具有良好的泛化性，为预测混凝土抗压强度提供了新的方法。

1  模型相关理论

1.1  极限学习机

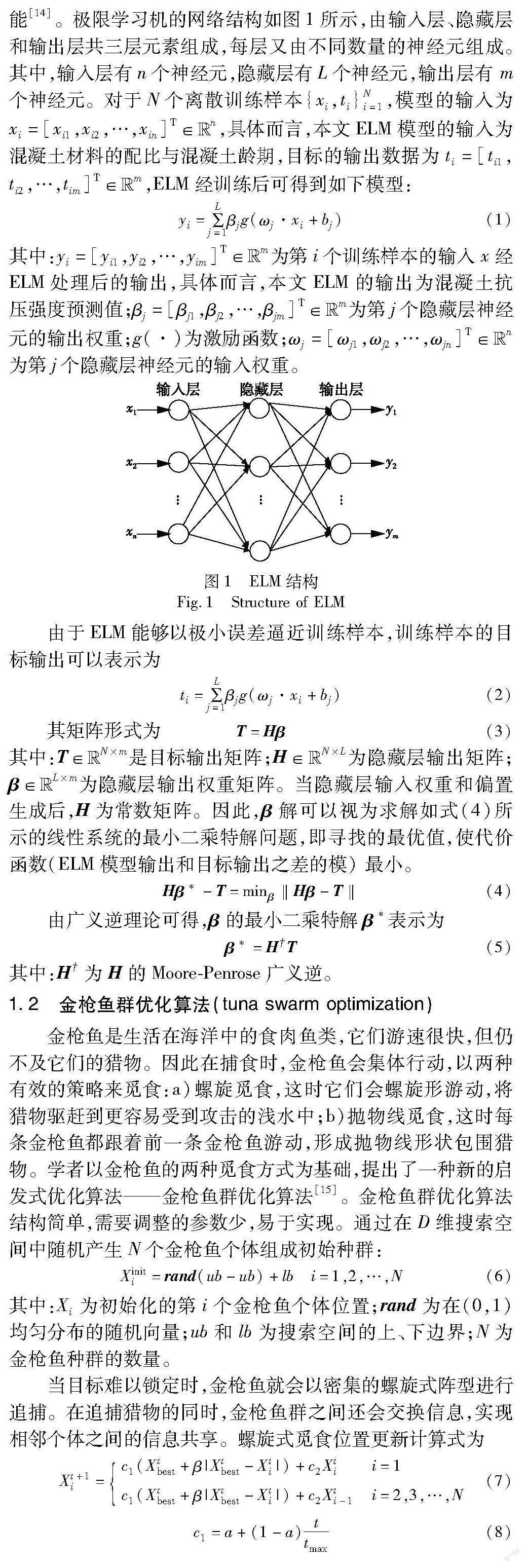
极限学习机是Huang等人于2004年提出的一种学习算法，旨在有效地训练单隐藏层前馈神经网络（single-hidden layer feedforward neural network，SLFN）［13］。ELM 的隐藏层输入权重和偏置可以随机生成，唯一需要确定的是隐藏层输出权重。除了学习速度极快外，极限学习机算法还表现出良好的泛化性能［14］。极限学习机的网络结构如图1所示，由输入层、隐藏层和输出层共三层元素组成，每层又由不同数量的神经元组成。其中，输入层有n个神经元，隐藏层有L个神经元，输出层有 m个神经元。对于N个离散训练样本{xi，ti}Ni=1，模型的输入为xi=［xi1，xi2，…，xin］T∈Euclid Math TwoRApn，具体而言，本文ELM模型的输入为混凝土材料的配比与混凝土龄期，目标的输出数据为ti=［ti1，ti2，…，tim］T∈Euclid Math TwoRApm，ELM经训练后可得到如下模型：

yi=∑Lj=1βjg（ωj·xi+bj）（1）

其中：yi=［yi1，yi2，…，yim］T∈Euclid Math TwoRApm为第i个训练样本的输入x经ELM处理后的输出，具体而言，本文ELM的输出为混凝土抗压强度预测值；βj=［βj1，βj2，…，βjm］T∈Euclid Math TwoRApm为第j个隐藏层神经元的输出权重；g（·）为激励函数；ωj=［ωj1，ωj2，…，ωjn］T∈Euclid Math TwoRApn为第j个隐藏层神经元的输入权重。

由于ELM能够以极小误差逼近训练样本，训练样本的目标输出可以表示为

ti=∑Lj=1βjg（ωj·xi+bj）（2）

其矩阵形式为  T=Hβ（3）

其中：T∈Euclid Math TwoRApN×m是目标输出矩阵；H∈Euclid Math TwoRApN×L为隐藏层输出矩阵；β∈Euclid Math TwoRApL×m为隐藏层输出权重矩阵。当隐藏层输入权重和偏置生成后，H为常数矩阵。因此，β解可以视为求解如式（4）所示的线性系统的最小二乘特解问题，即寻找的最优值，使代价函数（ELM模型输出和目标输出之差的模） 最小。

Hβ*-T=minβ‖Hβ-T‖（4）

由广义逆理论可得，β的最小二乘特解β*表示为

β*=HT（5）

其中：H为H的Moore-Penrose广义逆。

1.2  金枪鱼群优化算法（tuna swarm optimization）

金枪鱼是生活在海洋中的食肉鱼类，它们游速很快，但仍不及它们的猎物。因此在捕食时，金枪鱼会集体行动，以两种有效的策略来觅食：a）螺旋觅食，这时它们会螺旋形游动，将猎物驱赶到更容易受到攻击的浅水中；b）抛物线觅食，这时每条金枪鱼都跟着前一条金枪鱼游动，形成抛物线形状包围猎物。学者以金枪鱼的两种觅食方式为基础，提出了一种新的启发式优化算法——金枪鱼群优化算法［15］。金枪鱼群优化算法结构简单，需要调整的参数少，易于实现。通过在D维搜索空间中随机产生N个金枪鱼个体组成初始种群：

Xiniti=rand（ub-ub）+lb  i=1，2，…，N（6）

其中：Xi为初始化的第i个金枪鱼个体位置；rand为在（0，1）均匀分布的随机向量；ub和lb为搜索空间的上、下边界；N为金枪鱼种群的数量。

当目标难以锁定时，金枪鱼就会以密集的螺旋式阵型进行追捕。在追捕猎物的同时，金枪鱼群之间还会交换信息，实现相邻个体之间的信息共享。螺旋式觅食位置更新计算式为

Xt+1i=c1（Xtbest+β|Xtbest-Xti|）+c2Xtii=1

c1（Xtbest+β|Xtbest-Xti|）+c2Xti-1i=2，3，…，N（7）

c1=a+（1-a）ttmax（8）

c2=（1-a）-（1-a）ttmax（9）

β=eblcos（2πb）（10）

l=e3 cos （（（tmax+1/t）-1）π）（11）

其中：X为第t+1次选代的个体位置；Xtbest为当前最佳个体位置；c1和c2为重系数；t表示当前迭代的次数；tmax表示最大迭代次数；b为一个在（0，1）的随机数。当最优个体无法找到食物时，在搜索空间中随机生成一个坐标作为螺旋式觅食的参考点。

Xt+1i=c1（Xtrandβ|Xtrand-Xti|）+c2Xti

c1（Xtrand+β|Xtrand-Xti|）+c2Xti-1i=2，3，…，N（12）

其中： Xtrand表示在搜索空间中随机生成的坐标点。

金枪鱼除了螺旋式觅食之外，还有抛物线型觅食，即以食物为参照点形成抛物线，金枪鱼群通过在周围搜索来寻找食物的位置。具体数学模型如下所示。

Xt+1i=Xtbest+rand（Xtbest-Xti）+TF×p2（Xtbest-Xti）if rand<0.5

TF×p2Xtiif rand<0.5（13）

p=（1-ttmax）（t/tmax）（14）

其中：TF表示一個值为1或-1的随机数。TSO算法在整个优化的过程中，会不断地更新和计算直到满足最终条件。

2  基于金枪鱼群算法优化极限学习机的混凝土抗压强度预测模型的建立

混凝土作为一种复合材料、其抗压强度的大小主要取决于两方面因素。首先是拌合过程中加入的各种材料的配比，例如水泥、炉渣、粉煤灰、水、减水剂、粗骨料和细骨料等；其次，拌合完毕的混凝土需在自然环境中发生化学反应，待原料间相互作用后使得混凝土硬化，因此混凝土龄期与抗压强度也有很大相关性［16，17］。在前人研究的基础上，通过查阅大量相关文献以及总结工程经验分析，本文选择从混凝土材料配比与龄期两方面考虑对其抗压强度的影响，构建基于ELM的混凝土抗压强度回归预测模型。

同时，由于现场施工时对于混凝土强度预测的实时性与准确性均有很高要求，以便施工现场可以及时调整混凝土的材料配比。而在之前的相关研究中，大部分研究仅仅考虑提升混凝土抗压强度预测的精准度，而忽略了对预测耗时的要求。

TSO所具有的迭代次数少、寻优效率高等特征可以很好地满足这一需求，进而填补现有研究在这一方面的空缺。因此通过TSO对ELM中原先需要由经验手动设置的连接权值偏置值进行优化，进而提高强度预测的精准度与速度，以满足实际施工过程中的要求。TSO的优化运行流程如图2所示。

2.1  步骤1：建立初始指标体系与原始训练集

本实验采用UCI Machine Learning Repository分享的Concrete Strength数据集与Abobakr Khalil Al-Shamiri等在论文中公开的数据集。将其打乱后随机选取其中70%作为训练集，其余作为测试集。

2.2  步骤2：基于随机森林的输入变量选择

通过式（15）计算输入变量的重要性，得出不同的输入变量与输出变量之间的重要程度大小，进而对输入变量进行优化以提高模型性能。假设随机森林有N棵決策树，则某个变量的重要性I为

I=1N∑Ni=1（r1-r2）（15）

其中：r1为使用袋外数据计算的袋外误差；r2为随机变换袋外数据中某个变量的顺序后再次计算的袋外误差。

在计算出每个变量的重要性程度后，需要对这些输入变量进行组合，以不同变量组合时的均方误差（MSE）对训练集输入指标进行筛选，通过式（16）计算不同变量组合时的MSE，已得到MSE最小时的输入变量组合，并最终将筛选后的结果作为TSO-ELM模型的输入变量。计算公式如下：

MSE=∑ni=1（yi-y*i）2n（16）

其中：MSE为均方误差；yi为第i个样本的观测值；y*i为第i个样本的预测值；n为对应样本的样本容量。

2.3  步骤3：TSO-ELM模型的建立

a）获取已知的混凝土抗压强度训练数据与测试数据，并将两者均进行归一化处理。

b）设置ELM神经网络的参数，包括输入层节点数、隐含层节点个数等。

c）使用TSO算法进行优化以获取最优权值。具体而言，TSO算法将隐含层权重作为优化参数，将ELM的均方根误差作为适应度函数，通过不断迭代更新隐含层权重，以使适应度函数最小化。在每次迭代中，TSO算法采用抛物线觅食策略和螺旋觅食策略来更新种群个体，以增加搜索空间的多样性，同时通过记忆存储机制来避免陷入局部最优解，最终找到最优的隐含层权重，其具体流程如图3所示。

d）使用采用最佳参数的ELM神经网络进行训练，并使用测试集进行预测。

e）计算预测误差，并对预测结果进行统计，编入表格。

2.4  步骤4：预测结果评价

为了更好地验证模型的预测效果，本文采用均方根误差（RMSE）、平均绝对误差（MAE） 、拟合优度R2、迭代次数与预测耗时五个评价指标，相关的运算公式如式（17）～（19）所示。

均方根误差（root mean square error，RMSE）：

RMSE=∑mi=1（yi-y*i）2m（17）

平均绝对误差（mean absolute error，MAE）：

MAE=1m∑mi=1|yi-y*i|（18）

拟合优度（R2）：

R2=1-∑mi=1（yi-y*i）2∑mi=1（yi-i）2（19）

其中：m表示参与测试的混凝土样本个数；yi为第i个样本的混凝土抗压强度实际值；y*i为第i个样本经过计算的混凝土抗压强度预测值。

3  案例分析

3.1  实验数据获取及预处理

数据集1来源于University of California Irvine（UCI）平台提供的Machine Learning Repository中的Concrete Compressive Strength数据集。该数据集是由台湾中华大学叶怡成教授领导的小组在实验研究中获取，共有1 030组混凝土样本，数据样本数量较大，以此数据集可以验证模型的有效性。为研究原材料和混凝土龄期对混凝土强度的影响，选取选择水泥用量、粉煤灰、高炉矿渣粉高效减水剂、水含量、粗集料细集料以及混凝土龄期等八个影响因素作为输入变量，混凝土抗压强度作为输出变量，此数据集的部分数据如表1所示。

数据集2来源于文献[8]中公开的数据集。该数据集是由其在实验室中获取，共有324组混凝土样本。此数据集输入变量种类较少，因此无须进行变量的优化，以水泥用量、高效减水剂、水含量、粗集料、细集料五个影响因素作为输入变量，混凝土抗压强度作为输出变量。以此数据集可以验证本文模型的泛化性。此数据集的部分数据如表2所示。

3.2  输入变量选择与数据预处理

为了揭示每一类输入变量和最终输出变量之间相关性的大小，进而优化输入变量以获得更好的预测效果。通过MATLAB软件，以随机森林算法计算数据集1中的八个初始变量对输出变量的重要性指数，运行结果及重要性指数排序如表3所示。由表3结果可知，在输入变量中，混凝土龄期对输出变量抗压强度的相关性是最大的，即龄期的长短对混凝土抗压性能指标的影响最大，这与工程实际中的经验相符合，混凝土龄期的长短对混凝土性能指标的影响最大。而水泥含量、水的含量对输出的影响次之，这是因为水泥用量、水的含量和影响混凝土强度重要指标之一水胶比关系紧密。因此基于这一办法计算出的输入与输出之间的关系是合理的。

同时，利用MATLAB中heatmap方法分析输入变量与混凝土抗压强度之间的相关程度，从而对基于随机森林算法计算出的输入变量重要性评分作一个验证，分析结果如图4所示。图中系数大小和颜色深浅代表两个变量间的相关程度。

如图5所示，在遍历所有的特征变量后，得到最佳变量组合数六个，此时均方根误差值达到最小，模型的预测精度最高。结合表2特征的重要性排序进行递归特征后向筛选，得到的变量集合具体包括混凝土龄期、水泥用量、炉渣、高效减水剂、水的含量以及细集料六个影响因素，用于后文数据集1的混凝抗压强度预测模型的输入变量。同时，由于采集数据集中各个变量的差异较大，不属于同一个数量级，而且量纲不同，为了消除可能带来的影响，在建立回归模型之前，对训练集与测试集数据进行归一化预处理，如式（20）所示。

x′=x-min（x）max（x）-min（x）（20）

3.3  建立模型

将预处理完毕的混凝土材料数据代入本文模型中，以对混凝土抗压强度值进行预测并与真实结果进行对比。其中ELM的结构为9-9-1，即输入层9个节点，隐藏层9个节点，输出层1个节点，激活函数设置为sigmoid函数，核函数设置为高斯函数［9，18］。TSO中设置种群规模为20；搜索空间值在多次实验经验值的基础上获得，为避免意外情况，在考虑实际需求情况下略微增大搜索范围；每次运行的最大迭代次數为200。

3.4  运行结果

基于TSO-ELM的混凝土抗压强度预测模型是在Intel CoreTM i5-1035G1（8核），内存8 GB，Windows 10 64位操作系统，编程语言为MATLAB R2021a的开发环境中进行仿真实验，实验在两个数据集上均进行50次，结果如表4、5所示。

3.4.1  ELM算法测试

为验证ELM的泛化性能和计算效率，进行如下ELM、BP 神经网络和SVM的对比实验。BP网络与ELM采用相同结构，均为9-9-1，核函数均为高斯函数；SVM选取高斯核。实验使用数据集1分别进行50次，预测结果的各项评价指标最优值、最差值与平均值如表6所示。

从表6可知，ELM与SVM的预测耗时相近，均少于BP神经网络。虽然BP神经网络的预测精度最高，但由于 BP神经网络基于链式求导法则，以及误差反向传播方法迭代计算的特性，其预测过程所耗时间最长，同时还存在陷入局部最优的风险，难以用于实际施工生产当中。综上所述，ELM进行混凝土抗压强度的预测，相较于其他两种算法，ELM能更好地满足实际现场施工时对于混凝土抗压强度预测实时性与准确性的需求。

3.4.2  TSO超参数优化测试

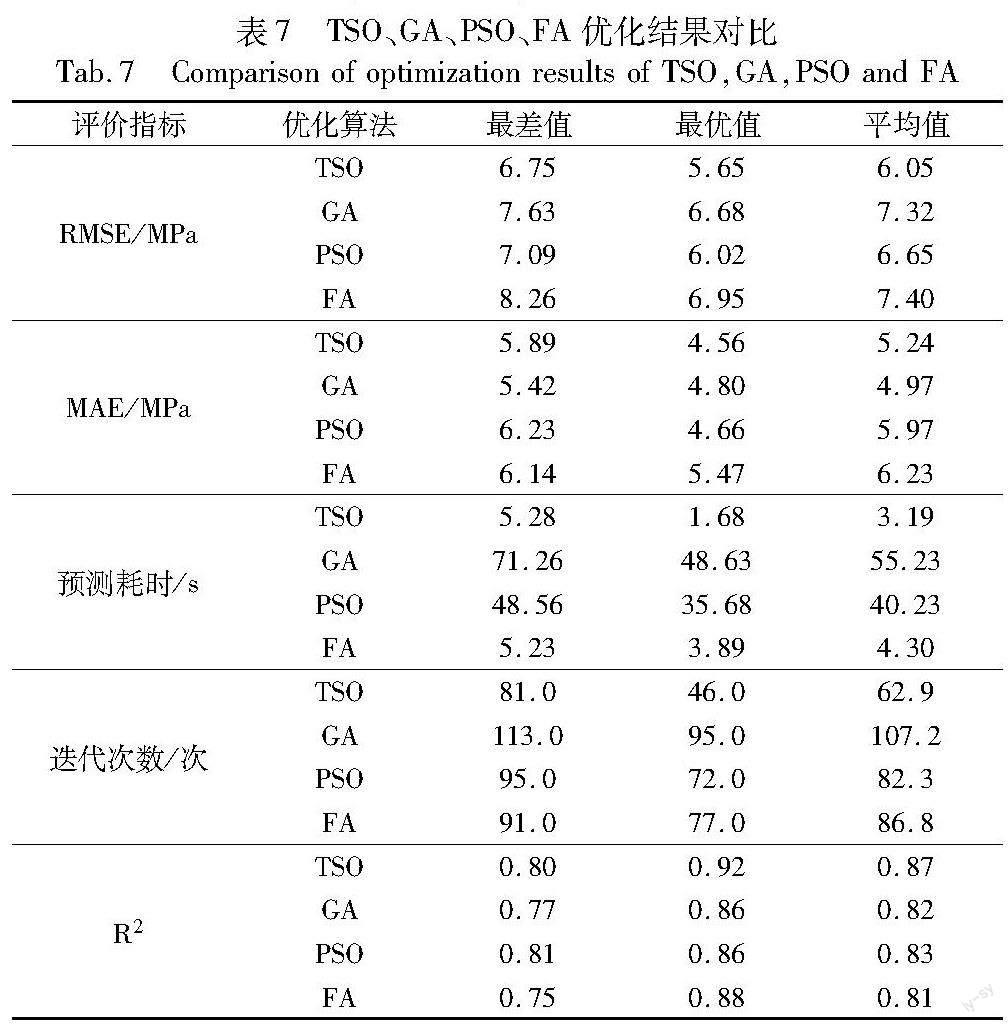
为了验证TSO的寻优能力，将其与在混凝土抗压强度预测领域常用的遗传算法（genetic algorithm，GA）、粒子群算法（particle swarm optimization，PSO）、萤火虫算法（fireflies algorithm，FA）优化的极限学习机进行对比实验，并将预测精准度作为评价指标，以判断这四种算法在应用于实际施工生产时是否具有高效性。

仿真参数设置：参数寻优算法中，GA法的搜索步长为0.5，采样函数使用expected-improvement-plus［19］；PSO中，惯性权重设置为0.6，学习因子分别设置为1.5与1.7，个体速度最大值与最小值分别为0.1与100［20］；FA中，种群规模均设置为20，最大吸引度值为2，光强吸收系数为1，初始化步长因子为0.2［21］。每种算法实验均独立进行50次，并且分别记录四种算法各项评价指标的最优值、最差值与平均值，以对算法的参数优化性能进行评价，评价结果如表7所示。

从表7得知，经过TSO优化后的混凝土抗压强度预测模型的预测精度要高于其他三种优化算法，而且也在更少的迭代次数中收敛，同时模型的运行速度较其他更快，能更好地满足施工现场对实时性的要求；经过GA优化后的模型精度虽然略高，但是其较长的预测耗时使其难以应用于实际施工生产中。综上所述，虽然经过四种算法优化后模型误差均在实际允许的范围内，但是TSO以其较低的计算复杂度、更少的迭代次数、更短的预测耗时、更优的预测精度，证明其在混凝土抗压强度预测问题模型的超参数寻优上具有高效性。

3.4.3  TSO-ELM模型泛化性能测试

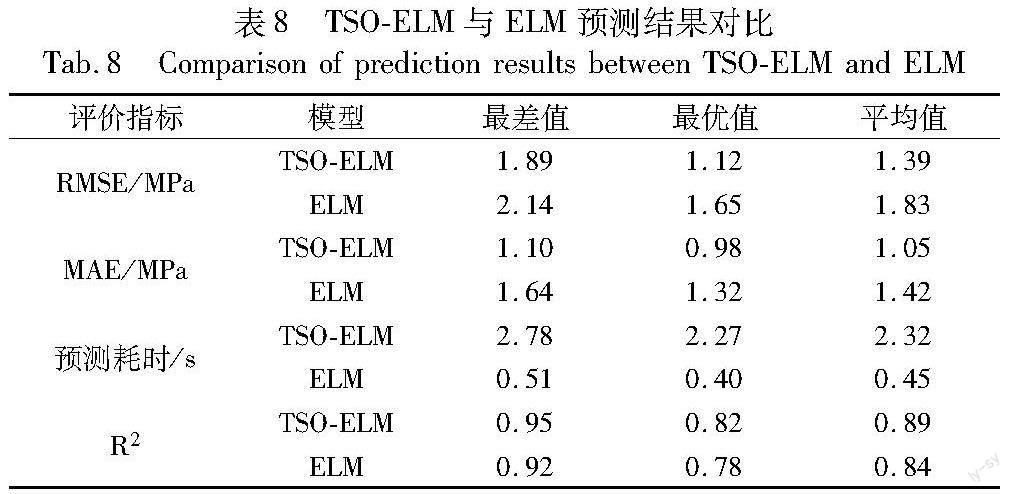
为了进一步验证TSO-ELM模型的泛化性能，以测试其在实际施工中的可行性，将其运用于数据集2，并以数据集2将结果与未经过参数优化的ELM进行对比。每种模型分别独立进行50次实验，记录各项评价指标的最差值、最优值及平均值，如表8所示。从表8可知，在混凝土抗压强度预测的精度方面，TSO-ELM优于未经参数优化的ELM算法，精确度提升约24%；由于使用TSO进行参数优化的迭代运算，虽然TSO-ELM模型的预测耗时相较于ELM稍长，但是仍然在现场施工允许的时间范围以内。综上所述，此实验结果表明，TSO-ELM模型在混凝土抗压强度预测上具有良好的泛化性能，同时能够较好地满足现场施工的要求。

4  结束语

针对混凝土抗压强度预测在施工现场对实时性与准确性具有较高要求的特点，本文采用预测耗时更短的ELM作为建模方法。由于ELM的预测表现极大程度上受到超参数的影响，为降低超参数寻优的耗时，本文选择TSO对 ELM的超参数进行寻优，建立基于TSO-ELM混凝土抗压强度预测模型，并且在两个公开数据集上进行了实验仿真，与使用GA、PSO、FA进行超参数寻优的模型的预测效果进行了比较。实验结果表明，TSO-ELM模型相较于其他模型能够更快速地完成预测，更准确地对混凝土抗压强度进行预测，并且此模型具有良好的泛化性，适合在实际施工现场对混凝土进行抗压强度预测。

参考文献：

［1］陈洪根，龙蔚莹，李昕，等.基于BP神经网络的粉煤灰混凝土抗压强度预测研究［J］.建筑结构，2021，51（S2）：1041-1045.（Chen Honggen，Long Weiying，Li Xin，et al.Prediction of compressive strength of fly ash concrete with BP neural network［J］.Building Structure，2021，51（S2）：1041-1045.）

［2］韩建军，赵道松，李建平.基于BP神经网络的垃圾飞灰混凝土抗压强度预测模型［J］.混凝土，2022（9）：78-81.（Han Jianjun，Zhao Daosong，Li Jianping.Prediction model of compressive strength of garbage fly ash concrete based on BP neural network［J］.Concrete，2022（9）：78-81.）

［3］郭耀東，刘元珍，王文婧，等.基于BP神经网络的再生保温混凝土抗压强度预测［J］.混凝土，2018（10）：33-39.（Guo Yaodong，Liu Yuanzhen，Wang Wenjing，et al.Prediction of compressive strength of regenerated the insulated concrete based on BP neural network［J］.Concrete，2018（10）：33-39.）

［4］曹斐，周彧，王春晓，等.一种改进的支持向量回归的混凝土强度预测方法［J］.硅酸盐通报，2021，40（1）：90-97.（Cao Fei，Zhou Yu，Wang Chunxiao，et al.An improved support vector regression method for concrete strength prediction［J］.Bulletin of the Chinese Ceramic Society，2021，40（1）：90-97.）

［5］李杨，刘庆华，郭天添.基于CART-SVR模型的混凝土抗压强度预测研究［J］.混凝土，2022（8）：40-44.（Li Yang，Liu Qinghua，Guo Tiantian.Prediction method of concrete compressive strength based on CART-SVR［J］.Concrete，2022（8）：40-44.）

［6］冯禹铭，董秀成，金滔.基于PSO-ELM的机器人精度补偿方法研究［J］.计算机应用研究，2019，36（10）：3000-3003.（Feng Yu-ming，Dong Xiucheng，Jin Tao.Research on methods of robot accuracy compensation based on PSO-ELM［J］.Application Research of Computers，2019，36（10）：3000-3003.）

［7］盛晓晨，史旭东，熊伟丽.改进粒子群优化的极限学习机软测量建模方法［J］.计算机应用研究，2020，37（6）：1683-1687.（Sheng Xiaochen，Shi Xudong，Xiong Weili.Soft sensor modeling of extreme learning machine based on improved particle swarm optimization［J］.Application Research of Computers，2020，37（6）：1683-1687.）

［8］Abobakr K A，Joong H K，Yuan Tianfeng.Modeling the compressive strength of high-strength concrete：an extreme learning approach［J］.Construction and Building Materials，2019，208：204-219.

［9］严东，汤健，赵立杰.基于特征提取和极限学习机的软测量方法［J］.控制工程，2013，20（1）：55-58.（Yan Dong，Tang Jian，Zhao Lijie.Soft sensor approach based on feature extraction and extreme learning machines［J］.Control Engineering of China，2013，20（1）：55-58.）

［10］吴小平，李元栋，张英杰，等.基于BOA-ELM的混凝土抗压强度预测研究［J］.计算技术与自动化，2020，39（1）：140-144.（Wu Xiaoping，Li Yuandong，Zhang Yingjie，et al.Prediction of concrete compressive strength based on BOA-ELM［J］.Computing Techno-logy and Automation，2020，39（1）：140-144.）

［11］薛萍，刘玲，王仰仁，等.基于金枪鱼群优化算法的Jensen模型参数求解［J］.排水灌溉学报，2022，41（11）：22-29.（Xue Ping，Liu Ling，Wang Yangren，et al.Calculating the coefficients in the Jensen model using the tuna swarm optimization algorithm［J］.Journal of Irrigation and Drainage，2022，41（11）：22-29.）

［12］赵力，史贤俊，秦玉峰.基于故障可诊断性定量评价的测试优化选择［J］.电光与控制，2023，30（8）：107-114.（Zhao Li，Shi Xianjun，Qin Yufeng.Test optimization selection based on quantitative evaluation of fault diagnosability［J］.Electronics Optics & Control，2023，30（8）：107-114.）

［13］Huang Guang，Zhu Qinyu，Siew C.Extreme learning machine：theory and applications［J］.Neurocomputing，2006，70（1-3）：489-501.

［14］Huang G B，Zhou Hongming，Ding Xiaojian，et al.Extreme learning machine for regression and multiclass classification［J］.IEEE Trans on Systems，Man，and Cybernetics，Part B：Cybernetics，2012，42（2）：513-529.

［15］Xie Lei，Han Tong，Zhou Huan.Tuna swarm optimization：a novel swarm-based metaheuristic algorithm for global optimization［J］.Computational Intelligence and Neuroscience，2021，2012：article ID 9210050.

［16］蒋泽中.高性能混凝土性能及抗裂细观机理研究［D］.成都：西南交通大学，2017.（Jiang Zezhong.Study on the properties and crack resistance microscopic mechanism of high performance concrete［D］.Chengdu：Southwest Jiaotong University，2017.）

［17］董方園，郑山锁，宋明辰，等.高性能混凝土研究进展Ⅱ：耐久性能及寿命预测模型［J］.材料导报，2018，32（3）：496-502，509.（Dong Fangyuan，Zheng Shansuo，Song Mingchen，et al.Research progress of high performance concrete Ⅱ：durability and life prediction model［J］.Materials Reports，2018，32（3）：496-502，509.）

［18］王江荣.基于灰色关联分析的极限学习机在混凝土抗压强度预测分析中的应用［J］.水泥工程，2017，177（3）：19-22.（Wang Jiangrong.Application of extreme learning machine based on gray relational analysis in prediction of concrete compressive strength［J］.Cement Enginee-ring，2017，177（3）：19-22.）

［19］陈浩，刘荣桂，闫乾勋，等.基于GA-BP神经网络的SAP内养护机制砂混凝土抗压强度预测［J］.混凝土，2023，403（5）：72-76.（Chen Hao，Liu Ronggui，Yan Qianxun，et al.Based on GA-BP neural network prediction of compressive strength of machine-made sand concrete with SAP internal curing［J］.Concrete，2023，403（5）：72-76.）

［20］龚珍，卜小波，吴浩.基于PSO-SVM的混凝土抗压强度预测模型［J］.混凝土，2013，290（12）：11-13.（Gong Zhen，Pu Xiaobo，Wu Hao.Concrete compressive strength test based on vector machine optimized by particle swarm optimization algorithm［J］.Concrete，2013，290（12）：11-13.）

［21］陈林，陈双庆.基于机器学习的橡胶改性再生骨料混凝土抗压强度预测研究［J］.公路工程，2022，47（5）：169-175.（Chen Lin，Chen Shuangqing.Study on prediction of compressive strength of rubber-modified recycled aggregate concrete based on machine learning［J］.Highway Engineering，2022，47（5）：169-175.）