数字图像相关方法中基于改进IC-GN算法高精度形变测量研究
孙泽刚, 张 奎*, 蒋 强, 黎军华
1. 四川轻化工大学机械工程学院, 四川 宜宾 644002; 2. 乐山师范学院电子信息与人工智能学院,四川 乐山 614000; 3. 乐山一拉得电网自动化有限公司, 四川 乐山 614000
数字图像相关方法(digital image correlation method,DICM或DIC)[1,2]根据物体变形前后的散斑图像,通过相关函数匹配散斑图像最相似子集的位置来获取物体的形变信息,也被称为数字散斑相关方法(digital speckle correlation method,DSCM),由Peters等[3]和Yamaguchi[4]于20世纪80年代提出。因为其具有无损、非接触性、低成本、对测量环境要求低等优点[5],DIC方法已在科学研究和工程实践中得到广泛应用,如土木工程[6]、航空航天[7]、工业制造[8]、材料科学[9]、自主驾驶技术[10]等。
在DIC方法中,提升测量精度的方法主要分为硬件和算法两个部分,通过提升硬件设施和改善环境对精度的提高是有限的,同时伴随着成本急剧增高、测量系统变得更加复杂,因此,从算法上提升精度成为了主要途径。DIC算法主要包括两个部分:整像素位移搜索和亚像素位移搜索。其中,亚像素位移搜索是影响DIC方法测量精度的主要因素。
在亚像素位移搜索研究方面,通常有梯度法、曲面拟合法等非迭代亚像素算法和灰度梯度迭代法、迭代曲面拟合法、前向加性牛顿-拉弗森迭代法(forward additive Newton-Raphson,FA-NR)[11]、反向组合高斯-牛顿迭代法(inverse composition Gauss-Newton,IC-GN)[12]等迭代算法。在2001年Zhou等[13]根据物体表面变形前后灰度值保持不变的原理,通过灰度梯度对亚像素位移进行测量,首次提出了基于梯度算法求解亚像素位移,并通过模拟散斑进行了验证;在2003年Hung等[14]通过选定拟合窗口,根据参考子区和目标子区之间的相关系数峰值来确定亚像素位移,提出了二次曲面拟合法,通过求解二次曲面的最大值来确定峰值处的亚像素位移;2007年Meng等[15]提出了一种基于迭代法和空间梯度的算法,即灰度梯度迭代法;2021年李荣丽等[16]通过比较不同的拟合曲面提出了一种迭代曲面拟合法;1989年Bruck等[17]将FA-NR算法应用到DIC技术中,其基本原理是通过迭代计算求解相关函数的极大(小)值,从而确定亚像素位移的位置,具有很高的精度;2001年Baker等[18,19]提出了IC-GN算法,并证明了逆合成算法和前向加性算法是等效的,并且IC-GN算法解决了FA-NR算法在迭代期间大量重复计算的问题,大大提高了算法的计算效率。在这之后,Pan等[20]在2016年研究比较了FA-NR算法和IC-GN算法,通过理论误差分析和数值模拟实验对比,证明了IC-GN算法具有更好的抗噪能力和更高的测量精度。至此,IC-GN算法奠定了在亚像素搜索算法中的重要地位。为了进一步提高IC-GN算法的精准度和效率,本文在IC-GN算法基础上,提出了一种基于灰度梯度的高斯-牛顿迭代法。
1 相关工作
1.1 理论基础
数字图像相关方法在测量物体形变大小时,通过在被测物体表面投影或绘制随机散斑图案,并定义相关函数,通过形函数描述形变前后的图像中像素点的形变信息,对物体变形前后两张图像进行分析求解得出最大(小)相关系数,该位置即为目标点在形变后在图像中的对应位置,其基本原理如图1所示。

图1 DIC基本原理示意图
在数字图像相关方法中,用形函数对图像变形前后的各个像素点位置关系进行描述,表达式如下:
(1)
式中的参数记为
P=[u,ux,uy,v,vx,vy]
其中,u和v分别表示x方向和y方向的像素位移,Δx和Δy分别表示子区中坐标(x,y)到子区中心坐标(x0,y0)的偏移量;ux和uy分别是位移不同方向的梯度。由式(1)可以得到图像变形前后对应点的关系为
(2)
(3)
在IC-GN算法中,零均值归一化差平方和函数(zero-mean normalized sum of squared difference,ZNSSD)[21]是最常用的相关函数,优点是收敛快、抗噪声、可靠性强等,表达式为

(4)
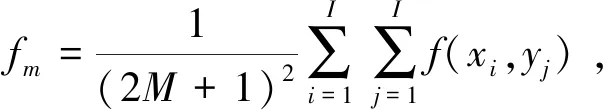
1.2 反向组合高斯-牛顿(IC-GN)算法
FA-NR算法在形变子区的图像上对形函数参数进行迭代更新求出最优解,Jacobian向量和Hessian矩阵每次迭代需要重新计算,使得计算量非常大,导致算法效率大大降低;IC-GN算法提出了新的思想,通过增量改变参考子区,匹配到与参考子区最相关的形变子区,得到新的形函数参数,再进行迭代优化求出最优解,示意图如图2所示。

图2 IC-GN示意图
用Pre来表示参考子区的形函数参数,Pde表示形变子区的形函数参数,参考子区的各个像素点可以表示为
xi=x0+W(Δxix0,Pre)
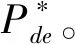
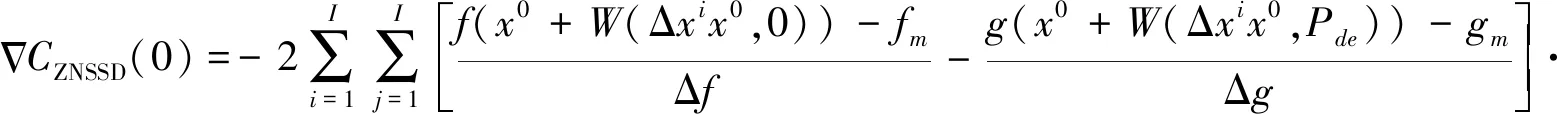
(5)
(6)
在光照均匀,亮度一致且散斑随机分布的条件下,可以对式(5)、式(6)化简得:
(7)
(8)
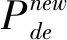
2 改进IC-GN算法
在对Hessian矩阵化简过程中,将式(6)的舍弃量记为A,则
(9)
式(9)由两个无穷小量相乘组成,分别记为A1、A2,则

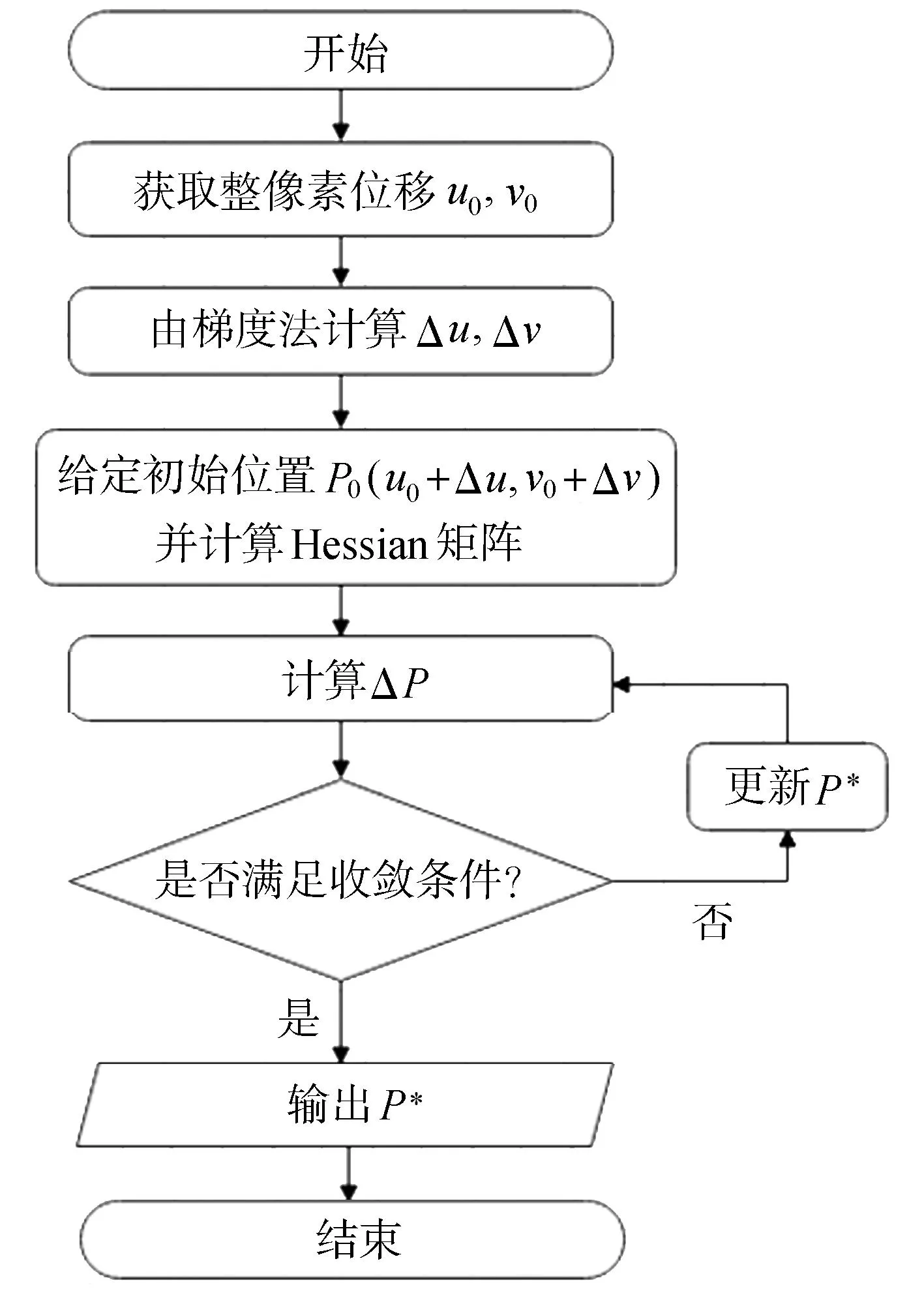
图3 GIC-GN算法流程图
GIC-GN算法主要分为三步,首先,由整像素搜索算法得到与参考子区对应的整像素位置;然后,根据图像发生形变后图像中各点的灰度值不变的原理,即
f(xi,yj)=g(xi′,yi′)
其中
xi′=xi+u+ Δx
yi′=yi+v+ Δy
u和v分别表示x和y方向的整像素位移,Δx和Δy分别表示x和y方向的亚像素位移,对g(xi′,yi′)进行一阶泰勒展开得
g(xi′,yi′) =g(xi+u,yi+v)+gx(x+u,yj+v)Δx+gy(xi+u,yj+v)Δy
将其代入最小距离平方和函数:
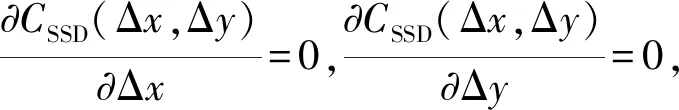
使用Barron算子对图像的梯度gx,gy进行计算,Barron算子表达式如下:
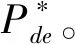
3 仿真实验
为验证GIC-GN算法能够实现对物体形变信息的高精度测量,本文通过计算机生成不同形变量的模拟散斑图像进行验证分析。首先,通过Matlab生成一幅512×512像素大小的参考图像,其散斑数量为2000,散斑大小为2 pixel,亮度为1。并通过设置参数生成了20幅从0.05~1 pixel形变量的参考图像。为了确定子区大小对算法精度的影响,分别对21×21、31×31、41×41、51×51、61×61五种子区大小在形变量为0.3 pixel的情况下进行了验证分析,为了保证实验结果的可靠性,本文对一个大小为100×100的子区,步进长度为10 pixel的100个像素点进行了测量,表1为不同算法测量的误差均值结果,表2为不同算法测量的标准差的结果,表3为不同算法测量所耗时间的结果。

表1 四种亚像素搜索算法的误差均值结果

表2 四种亚像素搜索算法的标准差结果

表3 四种亚像素搜索算法的消耗时间
从表1、表2、表3可以看出,随着子区的增大,算法的稳定性越来越高,所耗时间也随之增加,结合精度与效率的影响,在子区大小为41×41时,算法精度变化比较明显,此时GIC-GN算法相对常规的FA-NR算法和IC-GN算法精度提升了0.005 pixel,所消耗的时间仅仅是FA-NR算法的10.69%,是IC-GN算法的84.28%。
在确定所选子区大小后,本文对四种亚像素搜索算法从0.05~1 pixel形变量测量结果的误差均值和标准差进行了比较分析,表4为四种亚像素算法测量的消耗时间,图4表示四种亚像素搜索算法的误差均值结果,图5表示四种亚像素算法测量的标准差。

表4 四种亚像素搜索算法的消耗时间
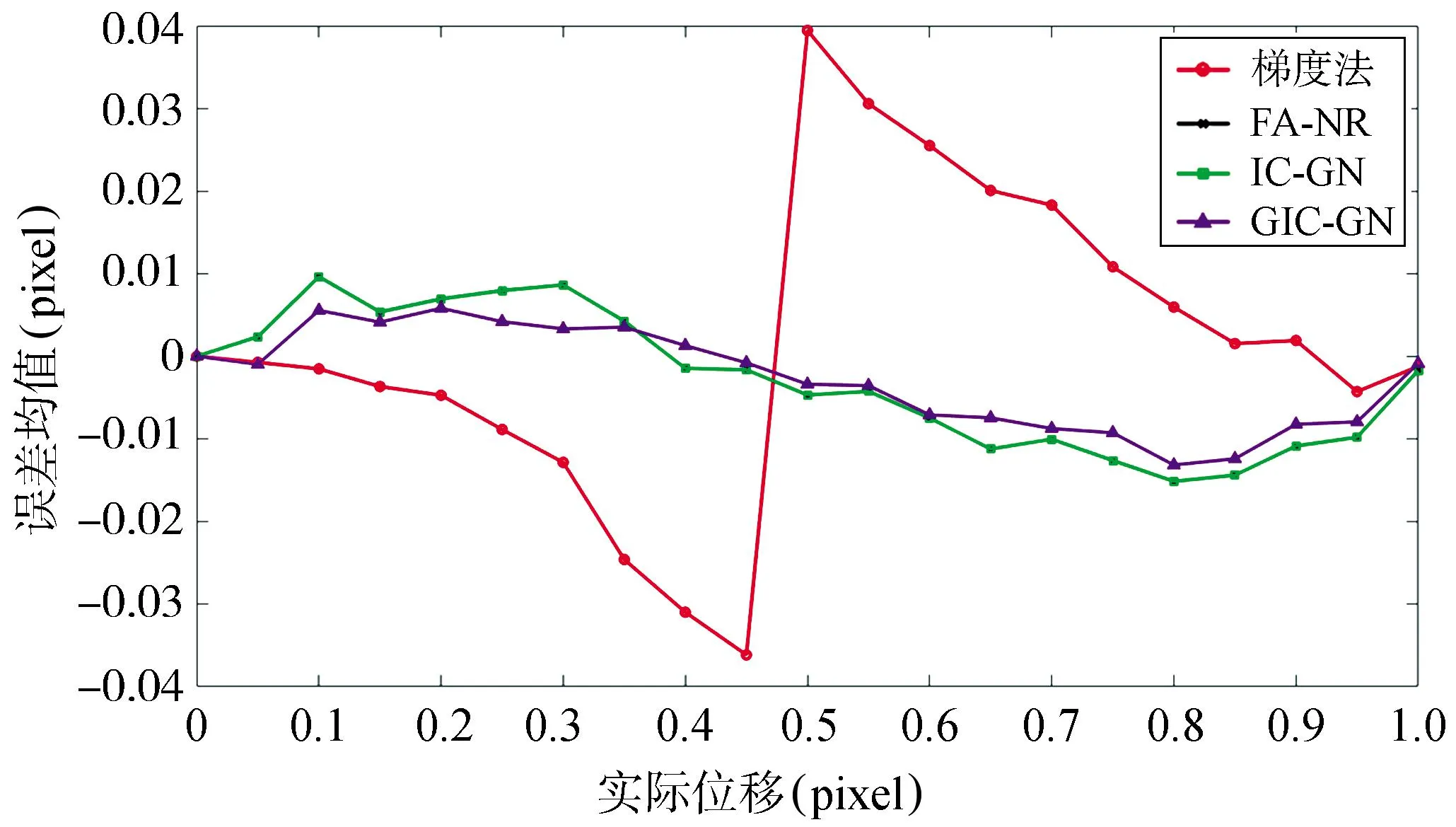
图4 四种亚像素搜索算法的误差均值结果
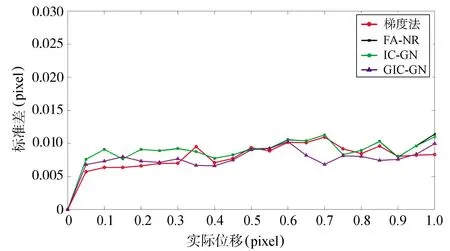
图5 四种亚像素搜索算法的标准差结果
从表4、图4和图5可以看出,FA-NR算法和IC-GN算法几乎拥有相同的误差和标准差,证明了FA-NR算法和IC-GN算法的等效性,而GIC-GN算法在精度和稳定度上比两种传统迭代方法都更加优秀,其均值误差能够稳定在10-4~10-3pixel,并且整个算法稳定性也能保持在10-3pixel,曲线相较于FA-NR算法与IC-GN算法更加平稳,同时在效率上相对IC-GN算法也有所提升。
4 结论
本文通过对IC-GN算法的原理介绍,提出了一种基于IC-GN算法的改进算法GIC-GN。通过分析Hessian矩阵计算过程中误差产生的原因,在已知整像素初始位置的基础上,使用梯度法求得亚像素位移代替整像素初始位置,减小Hessian矩阵计算过程中舍弃量过大产生的误差,提高对物体形变的测量精度,加快算法的收敛速度,提升算法的效率。并通过软件编程搭建了仿真实验平台,验证了本文提出的GIC-GN算法的可行性和精度,实验结果表明:GIC-GN算法精度比IC-GN算法提高了10%~60%,效率提高了20%。

