基于MOPSO-GRU神经网络的信号配时优化模型——以延安市交叉口为例

寇 洁, 李向有, 张雅楠, 胡 婷, 郭熊果

(延安大学 数学与计算机科学学院, 延安 716000)

0 引言

随着延安市城市化规模的不断扩大和人口数量的增加,延安市的交通压力越来越大,交通拥堵问题日益突出,并且逐渐成为制约城市发展和居民生活质量的重要因素[1]. 交通拥堵在一定程度上会增加市民的通勤成本和时间成本,增加交通事故的发生率,还会导致城市环境恶化. 这些问题既影响了市民的出行,也对城市的经济发展和社会稳定造成了一定的影响[2]. 因此为改善城市交通可持续发展和提高居民生活质量,本研究将对缓解延安市交通拥堵问题提出优化策略.

本研究是调查延安市老城区主要路段在特定时段的交通拥堵问题,选取延安市宝塔区杨家岭路段交叉口为研究对象,调查其相关交通数据、十字交叉口交汇点的通行状况、单双行道的分布及绿信比等,分析造成交通拥堵的各种因素,并通过设计优化策略,调整信号配时方案,缓解交叉口交通拥堵问题. 最后利用VISSIM仿真软件对比两相位交叉口和多相位交叉口优化前后的时延、队列长度等拥塞指标,展示方法优化效果. 基于以上分析,研究延安市交通拥堵问题的优化策略,具有重要的现实意义和理论价值.

1 交通组织分析

研究目的是缓解延安市交通拥堵问题,研究对象是由杨家岭隧道、杨家岭大桥和延大路组成的交叉口处的交通情况,对交叉口的现状画CAD图,如图1所示.

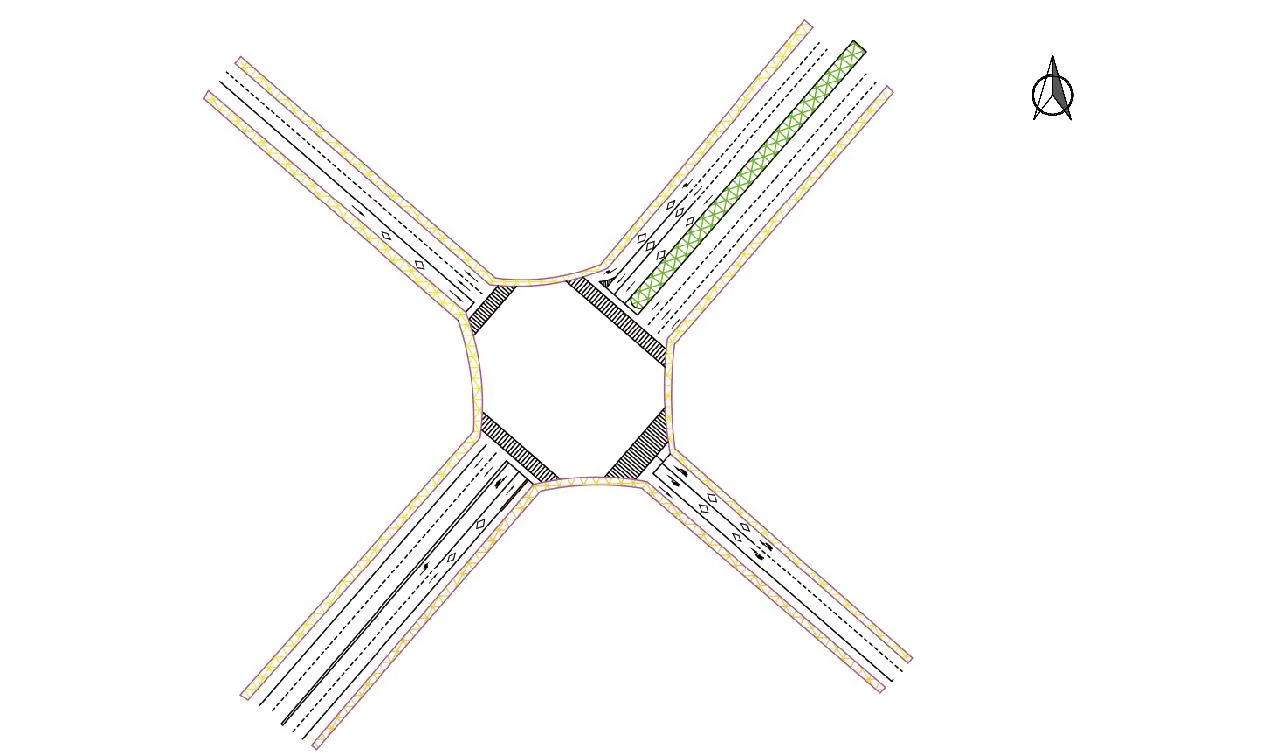
图1 杨家岭路段交叉口原状

杨家岭大桥的交叉口进口道为2条,有左转和直行,无右转,出口道2条;杨家岭隧道的交叉口进口道3条,有右转和直行,无左转,出口道3条;延大路由西北向东南方向的进口道1条,为公交车专用道,只有直行,出口道2条;延大路由东南向西北方向的进口道2条,有左转、右转和直行,出口道1条. 圣地路、杨家岭大桥、杨家岭隧道均无非机动车道. 杨家岭大桥的中央隔离设施为护栏;圣地路的中央隔离设施为黄实线隔离;杨家岭隧道的中央隔离设施为绿化带隔离.

杨家岭隧道是连接新区和老区的主要道路,由于其特殊的地理位置,经常会出现交通拥堵的情况. 具体表现为早、晚高峰时段车辆排队等待进出隧道,等待时间长,拥堵严重;隧道内车流量大,车辆行驶缓慢,拥堵严重;道路交叉口信号灯配时不太合理,隧道两侧车辆需排队等待进入隧道,影响周边道路的交通畅通. 拥堵情况在周五晚高峰时段和下雨天晚高峰时段颇为严重. 由于地形地势所限,在短时间内通过加宽路面和减少该路段的车流量不具有可行性,因此优化该道路交叉口信号灯配时,成为解决该交叉口拥堵的方案之一. 同时,为验证本文提出优化方法的适用性,本文分别采用杨家岭路段交叉口和1个四相位交叉口为研究对象,证明该优化方法在两相位及多相位交叉口同样具有优化效果.

2 相关工作

2.1 GRU循环神经网络

门控循环单元(Gated Recurrent Unit,GRU)为1种用于处理序列数据的循环神经网络(Recurrent Neural Network,RNN)的变体[1]. 于2014年由Kyunghyun Cho等提出,旨在克服传统RNN面临的梯度消失问题和长依赖问题.

杨家岭路段交叉口的交通流量是带有时间序列的数据,数据前后有较强的关联性. 使用神经网络模型预测时间序列数据表现出的性能较好,常用于时间序列预测的神经网络模型有RNN、LSTM、GRU. RNN循环神经网络模型可用于解决时间序列预测问题,网络的隐藏状态可捕获到当前时间步长的序列历史,并且模型参量不随时间步长的增加而增长. 但如果预测较长的时间序列数据,RNN会产生梯度爆炸和梯度消失的问题[4]. 为此,有学者提出将RNN隐藏层神经元改造成记忆神经元,引入门控循环网络,缓解RNN梯度消失带来的问题,控制信息流动,使模型更好地记住长远时期的信息. 长短期记忆网络(LSTM)模型中有遗忘门、输出门和输入门,可有效防止重要信息在数据训练时消失. GRU模型是改造了LSTM模型的记忆神经元形成的,计算收敛速度更快,并且两个算法预测精度相差不大,GRU模型较LSTM模型简单,其结构如图2所示[4]. 所以本研究选择GRU模型来预测交通流量,并结合粒子群算法优化信号配时,从而建立基于多目标粒子群算法-GRU循环神经网络的信号配时优化模型.

图2 GRU网络模型的架构

2.2 多目标粒子群优化算法

多目标粒子群优化算法(Multi-Objective Particle Swarm Optimization,MOPSO)为1种基于粒子群优化算法(Particle Swarm Optimization,PSO)的智能优化算法,广泛应用于解决具有多个优化目标的问题[6-8]. MOPSO算法的思想来源于对鸟群捕食行为的研究,该算法结构简单,操作起来容易实现,并且具有良好的全局搜索能力. 然而,MOPSO算法也存在收敛速度慢、容易陷入局部最优等问题,并不能保证找到全局最优解,因此在具体应用中需要根据实际情况进行参数设置和改进. 设计MOPSO算法的关键在于粒子的速度和位置的更替,进而粒子根据个体经验和群体经验的权重对速度和位置进行调整,使得粒子能在搜索空间中进行探索和利用信息,从而逐步寻找到最优解.

多目标粒子群优化算法的实现流程如下:

算法名称:多目标粒子群优化算法

算法功能:通过模拟群体行为实现全局搜索和解空间探索,以找到最优解.

输入:参数w:0.5～0.8;c1,c2:0.1～2;vmax,xmax:取决于优化函数.

输出:输出最优值.

过程:

步骤1：初始化粒子的速度和位置,设置粒子数量、迭代次数等参数;

步骤2：计算个体适应度;

步骤3：更替粒子速度→更替粒子位置;

步骤4：计算更新位置后的适应度,若新位置的适应度更高,则将该粒子的位置进行更替,否则不更替.

步骤5：判断是否满足终止条件,如果满足则退出,不满足则返回步骤2.

3 基于MOPSO-GRU神经网络的信号配时优化模型

3.1 MOPSO设计信号配时

3.1.1 目标函数

本研究选取的配时优化模型评价指标有延误(h),停车次数,通行能力(pcu/h)[9-15]. 由于3个评价指标的单位不同,需对单位进行统一,这样有助于简化计算和建立模型的过程. 进而对优化目标分别赋予不一样的权重系数X,Y,Z,建立式(1):

(1)

式中,D0为现状配时方案下的车辆延误;H0为现状配时方案下的停车次数;Q0为现状配时方案下的通行能力;X,Y,Z代表不同优化目标的权重系数,其中X+Y+Z=1,且X>0,Y>0,Z>0.系数越大,则对应目标需进行优化的程度也越大.

交通流量是个变量,影响交通流量的因素有很多,它随时间的变化而变化.本研究通过计算各相位的饱和流量比α,设置不同权重系数的变量,意味着对于交叉口不同相位的车流量分配给予不同的重视程度或优先级.通过设置权重系数,可调整各个相位在信号灯控制中的绿灯时间分配,以实现更合理的交通流调度.当交叉口处于低饱和状态时,α值相对较小,在所需优化目标中,主要控制车辆延误D和停车次数H最少;当临近饱和或饱和状态时,α值相对较大,在所需优化目标中,主要控制通行能力Q最大.因此,根据不同的交通优化需求目标,调节3个优化目标不同的权重系数.

因此,根据上述分析,将各个权重系数X,Y,Z分别设置为:

(2)

式中,C为交叉口的信号周期,α为各相位中最大饱和流量比.

则目标函数建立式(3):

(3)

式中,gi为相位i的有效绿灯时间;C为交叉口的信号周期;L为损失时间.

3.1.2 约束条件

信号灯在交叉口的实际运用中,信号周期C和绿信比λ都需要做一定的限制,不能设置的过大或者过小.一方面,信号周期时长过长时,在较长的绿灯时间的后期,车流较小,红灯方向车辆等待时间过长,导致道路交叉口冲突区域使用效率较低,造成道路交叉口通行能力降低;另一方面,信号周期时长较短时,红绿灯反复切换,导致车辆频繁停车等待,损失时间增加,车辆多次启动、停车,致使通行能力降低.因此合理的周期时长一般为24～180 s,因此最高值为180 s,最低值为24 s.最小周期时长确定见式(4):

(4)

式中,Cmin为最短周期时长(s);Y为全部相位的最大流量比之和;L为周期损失时间见(5):

(5)

式中,n为相位总数;li为第i个相位的损失时间.

各相位绿信比(1个相位内某一方向有效通行时间与周期长度之比)之和为定值见式(6):

(6)

式中,C为周期时长;G为周期绿灯总时间;Ye为周期黄灯总时间;L为周期总损失时间.

3.2 数据集与优化结果

建立MOPSO-GRU算法的目标是为了设置较为合适的信号配时,模型中的GRU负责预测交通流量. 本研究采用人为拍摄道路交叉口交通情况进行记录车流量数据,将车流量按照5 min为间隔建立数据集,数据集分成训练集和测试集,使用GRU模型对交通流量进行预测,将均方根误差(RMSE)、平均绝对误差(MAE)、准确率(ACC)作为模型预测精度评价指标[14]. 结果如图3所示.

图3 GRU模型预测某道口4月7日车流量结果展示

为验证本文提出的信号配时优化方法在两相位交叉口和多相位交叉口均可提高交叉口运行效率,本文选取了1个两相位交叉口和1个四相位交叉口作为实验对象.

3.2.1 两相位交叉口

选取GRU测试集预测值的高峰小时交通量作为粒子群算法调优的输入数据,两相位交叉口其数据展示如表1所示.

杨家岭路段交叉口是两相位交叉口,交叉口信号控制方案如图4所示.

3.2.2 四相位交叉口

为验证本文所提出信号配时方法在多相位交叉口上的适用性,本文采用了1个四相位交叉口作为研究对象,该交叉口东西走向为平安路,南北走向为世纪路,其数据展示如表2所示.

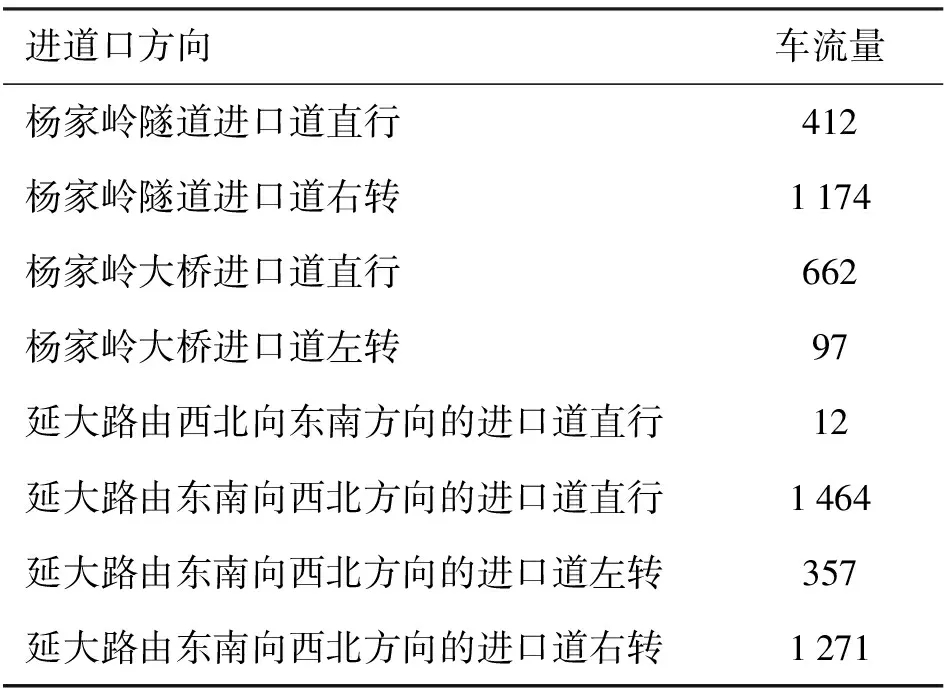
表1 两相位交叉口高峰小时交通量

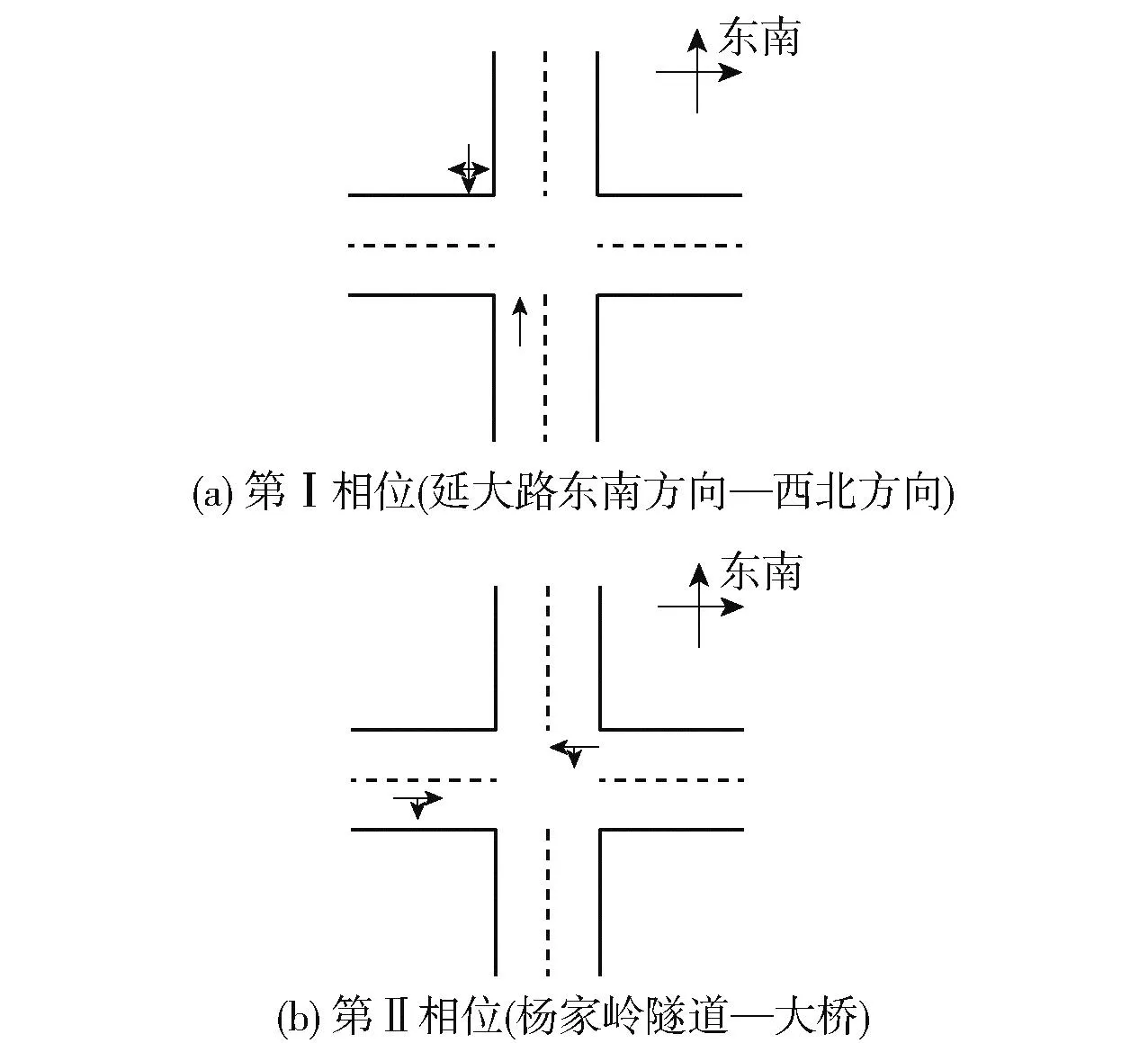
图4 两相位交叉口相位图

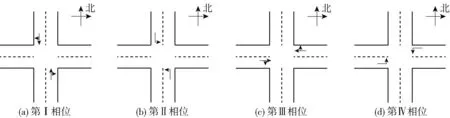
图5 四相位交叉口相位图

平安路—世纪路交叉口是两相位交叉口,交叉口信号控制方案如图5所示.

3.2.3 实验结果

以两相位交叉口为例,利用MOPSO算法进行实验,相关参数设置如下:黄灯时间及各相位损失时间都为3 s;粒子群初始数量为100,迭代次数设为100次,加速常数C1和C2设为1.5;最大有效绿灯时间、最小有效绿灯时间分别为90 s、10 s,最大周期时长设为180 s.

粒子分布的初始状态如图6(a)所示,迭代20、50、100次下,粒子的分布状态分别如6(b)～(d)所示.

图6 粒子迭代示意图

图6(a)为初始状态下粒子位置图,图中的粒子较为分散,红色的点代表初始化时最优解的位置. 1张图中有4小幅图,前3幅图是粒子变化的二维图,第4幅图是粒子变化的三维图. 根据图 7粒子迭代过程,可看出:随着迭代次数的增加,结果趋于稳定状态. 对于杨家岭路段交叉口的情形,预设信号配时优化方法,迭代60次后,粒子群逐步向最优解靠近. 3项评价指标也逐渐趋于稳定达到最优解.

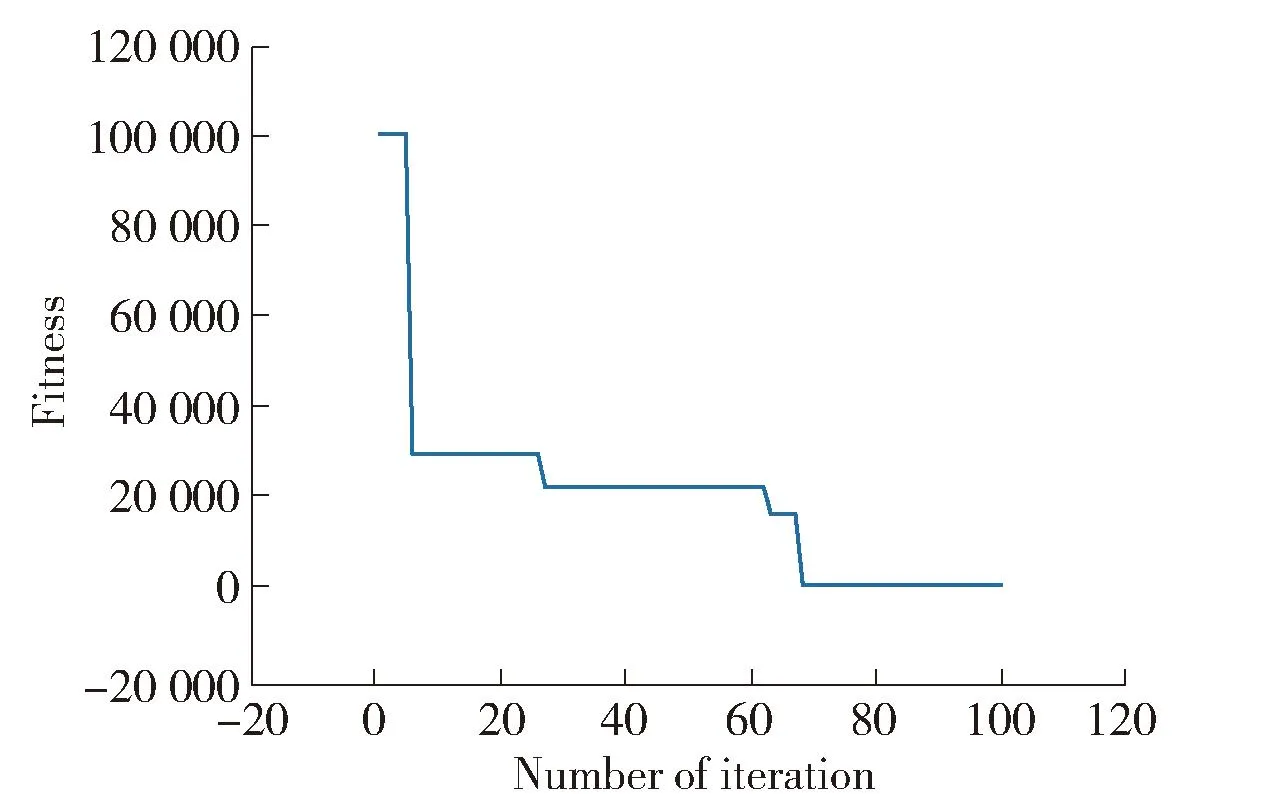
图7 迭代过程

以两相位交叉口为实验对象,程序运行结果为:相位Ⅰ绿灯时间为76 s,相位Ⅱ绿灯时间为66 s,信号周期为148 s.

以四相位交叉口为实验对象,用同样的方式优化四相位交叉口,程序运行结果为:相位Ⅰ绿灯时间为48 s,相位Ⅱ绿灯时间为18 s,相位Ⅲ绿灯时间为46 s,相位Ⅳ绿灯时间为23 s,信号周期为150 s.

4 MOPSO-GRU模型的VISSIM验证

本研究首先对杨家岭路段交叉口的交通组织进行优化,其次优化信号配时,不优化交叉口的相位,最后完成交叉口路网的绘制和相关参数设定,对优化前后2个道路交叉口进行仿真[17-18]. 仿真路网中车道数按杨家岭路段交叉口的渠化条件设置,车道宽度均设置为3.5 m. 杨家岭隧道至杨家岭大桥的饱和交通流量为1 600 pcu/h,延大路东南方向至西北方向的饱和交通流量为1 464 pcu/h. 车辆构成和车速等均采用VISSIM的默认值. 黄灯时长、各相位损失时间均设置为3 s. 信号配时设置时间由优化前后配时方案的结果决定,图8(a)为两相位交叉口原信号配时,图8(b)为粒子群算法优化后的两相位交叉口信号配时. 最后运行仿真模型得到仿真后各评价指标的值.

为验证本文所提出信号配时方法在多相位交叉口上的适用性,也对四相位交叉口进行了仿真验证,图9(a)为四相位交叉口原信号配时,图9(b)为粒子群算法优化后的四相位交叉口信号配时.

图8 两相位交叉口优化前后信号配时对比

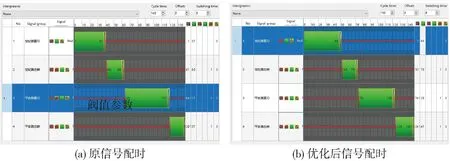
图9 四相位交叉口优化前后信号配时对比图

对优化前后两相位交叉口和四相位交叉口分别进行仿真,仿真持续3 600 s,仿真结果对比如图 10所示.

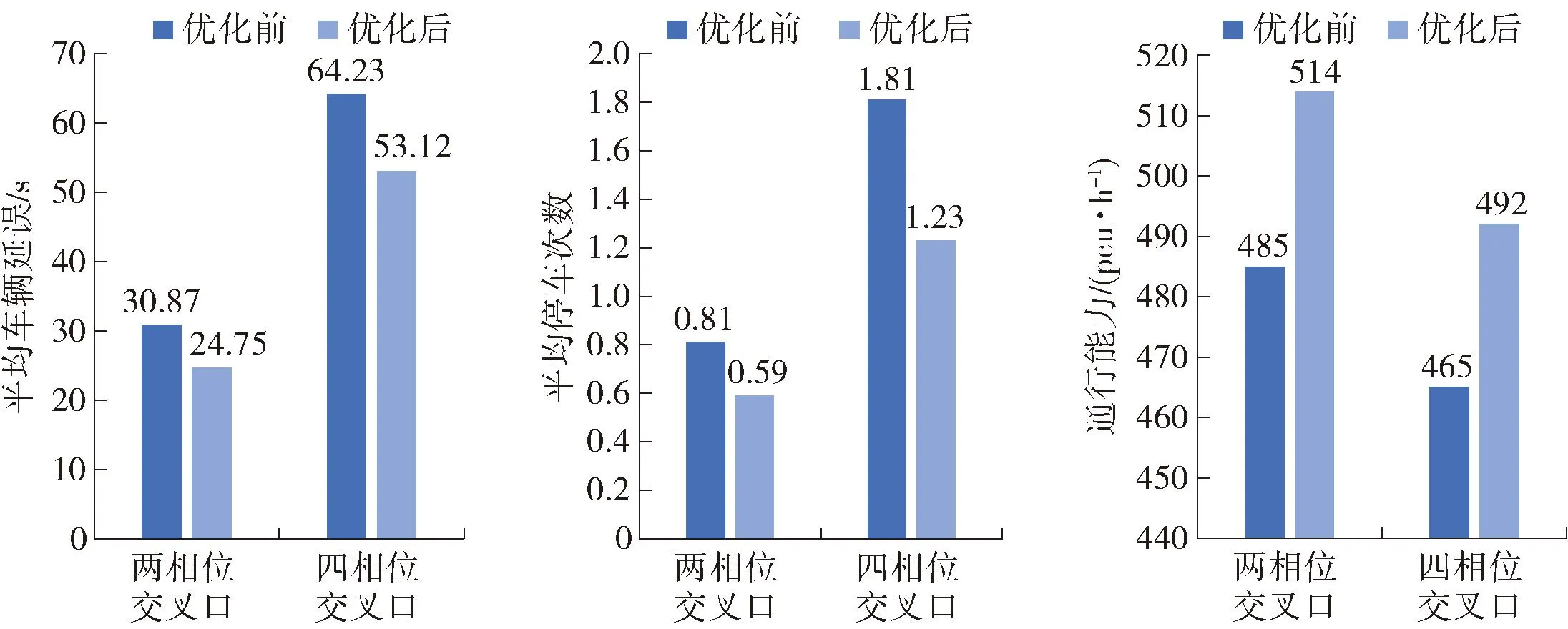
图10 优化前后评价指标结果对比

根据图8显示,杨家岭路段交叉口在优化前的信号周期时长为110 s,而优化后的周期时长为140 s,导致周期时间增加的原因是:在优化信号配时过程中,为了实现交通流的高效运行,会增加某些进口道的绿灯时间,以便更多车辆通过. 这样一来,路口的总车流量会增加,从而导致信号周期时间增长.

杨家岭路段交叉口在优化前的绿灯信号时长为70 s,优化后的绿灯信号时长为76 s,而优化之后绿灯配时没有发生很大变化,原因为:在优化信号配时过程中,优化目标与绿灯时长的变化之间存在一定的权衡关系,因此最终的配时结果可能在一定程度上保持稳定.

根据优化前后评价指标结果对比可知,两相位交叉口在新的配时方案下平均车辆延误降低了19.83%、平均停车次数降低了27.16%、车辆通行能力提高了5.98%,四相位交叉口在新的配时方案下平均车辆延误降低了17.29%、平均停车次数降低了32.04%、车辆通行能力提高了5.81%.

综上所述,使用本研究提出的信号配时优化模型,可显著改善交叉口的交通状况. 车辆的延误减少,停车次数减少,通行能力提高,这意味着车辆能更加顺畅地通过交叉口,交通效率得到了提升.

5 结束语

交通拥堵问题是城市发展过程中普遍存在的问题,缓解交通拥堵问题需要综合运用各种措施和方法,找到最优解决方案. 本研究首先分析了杨家岭路段交叉口目前存在的问题,继而对交通组织结构进行优化. 之后构建了GRU模型对交通流量进行预测,预测结果接近杨家岭路段交叉口车流量真实值,误差较小. 然后引入MOPSO算法作为解决方案,本研究将MOPSO和GRU结合,应用于信号配时优化问题,将交通流量预测数据的最大值作为粒子群算法调优的输入数据,得到优化后的信号配时方案. 最后搭建VISSIM仿真平台,分别使用了两相位和四相位的交叉口为实验对象进行验证,对比优化前后的实验数据,验证MOPSO-GRU模型的合理性. 实验结果表明,本研究所提出的基于MOPSO-GRU神经网络的信号配时优化模型可较好提高交通流量的效率和整体交通系统的性能.