多源空间数据辅助的云台控制摄像机几何定位方法

孟小亮，胡予萱，王明霞，周志宇，刘昆波，王 腾，高 广

（1.武汉大学 遥感信息工程学院，湖北 武汉 430079；2.江汉大学 人工智能学院，湖北 武汉 430056；3.广东省国土资源测绘院，广东 广州 510663；4.宝略科技（浙江）有限公司，浙江 杭州 315042）

随着科技的快速进步和创新，定位技术在各个领域中变得越来越普遍和重要。借助摄像机来实现定位功能的方法日益常见，而用于监控的摄像机主要包含2 种：固定式和可转动式。传统单目相机定位的研究主要集中在理想条件下使用固定中心投影相机的小范围定位[1]，难以满足现有杆塔摄像机监测应用场景中全方位和大范围等需求。因此，能够调整水平，俯仰角且可进行焦距变换的PTZ摄像机就得到了大家的青睐[2-5]，PTZ摄像机也可称为云台控制摄像机，由CCD高清摄像头，360°全景变换云台和一些相关的附属设备组成[6]。

在上世纪末，基于PTZ摄像机的智能视频监控在国外已迅速发展，美国国防部率先启动了VSAM[7]。尽管我国在PTZ摄像机的研究应用方面起步较晚，但现在也逐步赶上。2011 年清华大学研究人员采用2 个PTZ 摄像机开发出仿变色龙跟踪系统[8]。2013 年中南大学研究人员实现了一种用于交通监控的PTZ 球机的运动目标自主跟踪系统[9]。2016 年电子科技大学研究人员设计了一个多PTZ 摄像头的目标检测定位系统[10]。这些利用PTZ 的系统在其跟踪与定位上都有较好效果，但由于都只利用了单一相机所提供的参数，在精准定位上有所欠缺。因此，本文提出一种利用多源空间数据辅助PTZ 摄像机实现定位的方法。首先利用DSM 数据和卫星影像提供地理空间信息对PTZ 采集影像进行内业“刺点”和位姿解算，形成基准数据库；然后通过图像检索与特征点匹配获取基准数据库中的控制点信息完成影像定向，最后通过姿态射线-DSM 求交实现兴趣点定位；该方法不仅减少了外业的人力成本，而且可以适应缺少相机内参的环境，确保了目标位置的定位精度和稳定性。此外，利用高塔视频定位技术，可以自动监测和定位高塔周边区域，从而替代人工监测，提高效率并降低人力成本。

1 方法技术路线

本方法以高精度卫星产品数据源作为参照，以内业少量“刺点”取代外业密集“布控”，结合摄影测量相关理论，最终实现PTZ 摄像机高精度几何定位。方法包含3 个部分：控制数据集制作、图像检索与定向、目标几何定位。首先，利用已有高精度DOM 与DSM 作为控制数据源，选取不同方位摄像机样本影像，制作控制数据集。随后，利用图像检索与特征点匹配，将待计算影像与控制数据集进行匹配，获取特征点与对应三维坐标，进行影像位姿解算。最后，利用高精度DSM 作为约束，通过姿态射线-DSM 求交解算待定点的地面坐标，完成目标点位几何坐标计算。方法技术路线如图1所示。

图1 方法技术路线

1.1 控制数据集制作

本文利用摄像头采集的场景影像构建基准数据库，首先获取摄像机拍摄实验区域视频数据；然后抽取、筛选视频帧；再参考实验区DOM 及DSM 控制数据进行人工刺点；最后利用后方交会等位姿求解方法得到带位姿影像，构成基准数据库。

本文实验区域位于湖南省湘潭市湘潭县排头乡排头紫山，摄像头经纬度坐标为112.676 389，27.624 520，高度为39.9 m，实验区域包括以摄像头为中心，水平距离2 km以内的监测范围。以15°俯仰角（T）采集间隔，20°水平角（P）采集间隔，在参数T为1.0和2.0 时分别进行摄像头视频数据采集，保证尽可能覆盖设备监视范围之内的地物。在采集的同时，记录摄像机监测平台提供的影像PTZ 参数以供后续的图像检索使用。在保证抽取留下的影像图满足匹配标准的情况下，对已经获得的影像进一步抽帧筛选。筛选主要包括去除模糊或者低对比度（暗沉的）影像、去除重叠影像、去除无重要特征的大片树丛影像。筛选的作用是为了确保匹配的准确性和可靠性，防止因为影像质量差而导致匹配失败或误匹配。

实验区控制数据来源于资源三号线阵影像和高分七号立体影像。其中，资源三号线阵影像正视地面分辨率为2.1 m，前视和后视地面分辨率为3.5 m；高分七号立体影像后视地面分辨率为0.65 m，前视地面分辨率为0.8 m。经过几何处理后，得到地面分辨率5 m的DSM和分辨率0.7 m的DOM。其中DOM的几何精度优于3 m，DSM的几何精度优于5 m。人工刺点主要选择的特征点类型有池塘角点、道路拐点、田埂角点、房屋下角点四类。具体流程是：首先从摄像机图像中均匀选择一定数量的特征点，随后在卫星DOM 上对每个特征点拾取其平面坐标，再利用平面坐标在DSM上内插其高程。需要注意的是，一张影像需要至少8 个分布均匀的控制点，并且利用多余控制点进行精度检查。通过反复调整与删减控制点，直到检查点精度均小于3 m时为止。

1.2 图像检索与定向

对于输入的待计算图片，需要通过图片检索从基准数据库中获取相似拍摄角度和焦距的邻近影像，然后通过特征点匹配获取影像的空间信息。本文采用基于词汇树的图像检索算法和sift 特征提取算法，最后利用双向匹配[11-12]方法匹配特征点。

在基准数据库的构建和待定位影像的定向中，均需要对相机姿态求解。针对不同的需求，本文提出了2 种求解精确内外方位元素的方法：如果当前影像给出了内方位元素的初始值，则采用单片空间后方交会法求解精确内外方位元素；如果当前影像没有给出内方位元素的初始值，则采用直接线性变化方法，通过建立控制点二维像点坐标到三维地面坐标之间的映射关系，求解内外方位元素。

1.2.1 基于词汇树的图像检索算法

在本文中利用PTZ摄像机获取影像的水平旋转角度（P）与俯仰角度（T）筛选出基准数据库中类似角度的图片，缩小图片检索范围。然后，利用分层词汇树[13-15]进行影像相似度计算，以检索出最为相似的控制片影像。

本文采用SIFT特征向量集合进行词汇树构建。提取影像的SIFT特征后，利用K-means算法将特征向量集合划分为几组，每组由特征向量集合中距离该组聚类中心最近的描述子组成。然后将该过程递归应用到每组描述子向量中，从而将其划分为新的k组，每层都重复上述过程，直至达到词汇树深度d，k的经验值一般取10。

当词汇树创建完成后，每张影像则可以表示为加权后不同视觉单词的组合。采用影像检索系统中的倒排索引方法，对不同的视觉单词计算对应权重，然后计算两张影像的相似性得分因子。影像相似度计算过程如图2所示。

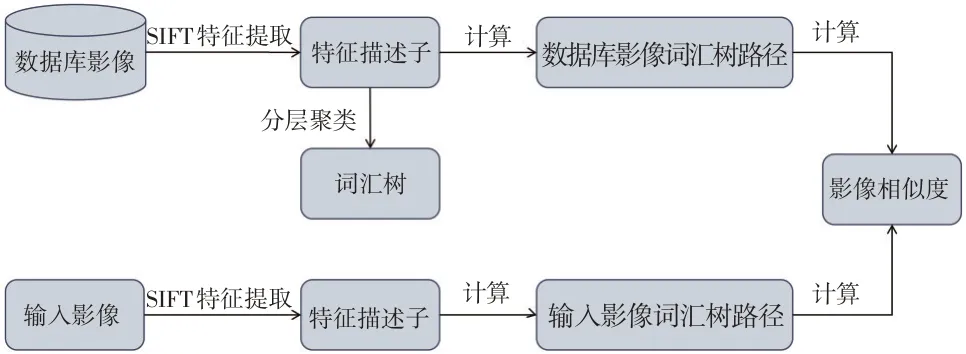
图2 影像相似度计算过程

1.2.2 特征点提取与匹配

本研究中采用SIFT特征提取算法[16]对待计算影像和检索出最相似的样本控制片影像的特征点进行匹配，然后在完成特征点的匹配后，将样本控制片特征点的三维坐标信息赋予待计算影像。

只有在参考影像和待配准影像之间找到一定数量的同名特征点，才能从待配准影像中获取足够的控制点信息，从而进行云控制摄影测量[17]。因此，特征点的匹配情况是影响基于影像特征库的云控制摄影测量精度的主要因素。本文通过计算特征向量的欧氏距离[18]来判断2 个特征点是否为匹配点，并使用双向匹配[11-12]，即取2 次单向匹配结果的交集作为匹配点集，从而提高匹配的精确度。

在参考影像中寻找其最邻近与次邻近的关键点，获得其特征向量之间最邻近与次邻近欧氏距离的比值与设定的匹配阈值T作对比，如式（1）：

式中，Dmin为关键点与其待匹配影像上特征点之间特征向量欧氏距离的最小值；DSecmin为2点特征向量欧氏距离的次小值。若两者的比值小于匹配阈值，则该关键点与参考影像中的最邻近关键点为一对匹配点。针对摄像机监测场景，经验阈值是0.5 时特征点的匹配效果较好。

1.2.3 影像定向

利用匹配得到的连接点，通过相对定向，可以获取待计算影像的位姿初始值，随后利用控制点后方交会或直接线性变换模型计算最终位姿参数。

1）后方交会法。由共线方程原理，可知像点坐标为观测值，所以将像点坐标量测值作为观测值，将单张影像的内外方位元素及畸变系数作为未知数建立误差方程，如式（2）。

式中，采用的畸变模型如式（3）；k1、k2为径向畸变系数。

将式（2）进行线性化，化简可得如下式（4）：

式中，X、Y、Z为已知的地面控制点坐标；Xs、Ys、Zs为未知的待确定点坐标；A为外方位元素改正数的系数；C为内方位元素改正数系数；D为检校系数改正数系数；V为像点坐标的残差；t、x2、xad分别为外方位元素改正数、内方位元素改正数、检校系数改正数。

按照式（5）对式（4）进行法化求解，解算得到各未知数的改正数：

由于有13个未知数，故需要至少7个控制点才可以完成解算，将未知数改正后代回，进行反复迭代，直至改正数小于给定阈值后停止迭代，得到未知数的精确解。

2）直接线性变换法。直接线性变换是建立像点坐标和相应物点物方空间坐标之间直接的线性关系的算法。式（6）为直接线性变换的一般形式：

式中，x、y为图像坐标；X、Y、Z为物方空间坐标。由于该线性方程并不严格，所以解算出的系数并不能直接当作准确值使用，而是为后续精确解的解算提供初值。

由于影像成像可能发生畸变，所以在直接线性变换一般式的基础上增加偏心畸变和径向畸变的畸变改正系数，如式（7）所示，以提升解算精度。其中，畸变模型同式（8）。

在解算出像点坐标的径向畸变和偏心畸变参数后，还需对原始像点坐标做畸变改正，以便后续使用立体像对解算物方点。在解算完成2 张相片的直接线性变换系数和畸变系数后，可对相片重叠区域的像点计算其对应的三维空间物方坐标。

1.3 目标几何定位

由于像主点到特征点的射线上的所有空间三维点的反投影像点都在同一位置，所以即使获取了视频帧的投影矩阵，也无法实现从二维到三维的计算。因此本文利用DSM作为约束，通过高程迭代内插方式逐渐逼近特征点的真实地面坐标，而基于高精度DSM的单视图特征点位地面坐标解算的关键在于如何实现射线与不规则DSM 面的求交，本文通过高程迭代逼近的方式实现精准定位，其具体计算过程如图3所示。

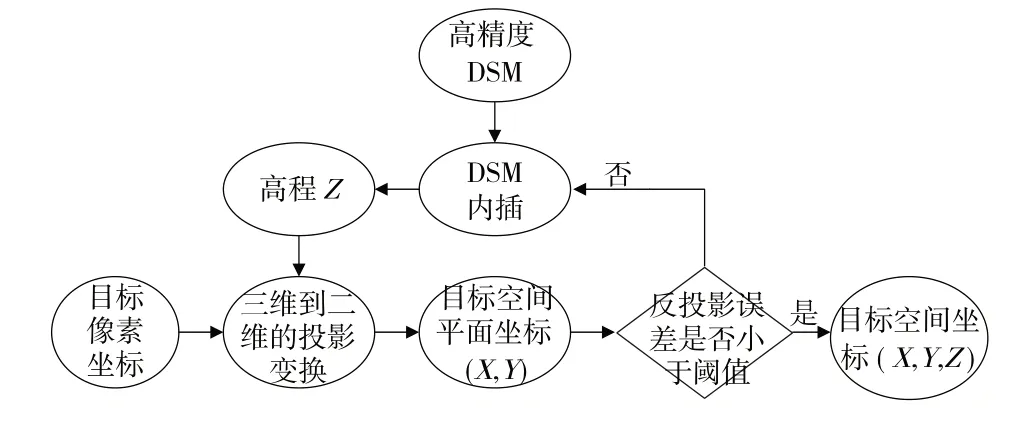
图3 基于高精度DSM的单视图特征点位地面坐标解算流程

如图4所示，利用投影矩阵P，可以建立从像素坐标（x,y,1）到世界坐标（X,Y,Z,1）的投影变换，即（x,y,1）=P（X,Y,Z,1）。但对一个特征点而言，只能建立2 个方程，而未知数有3 个，即（X,Y,Z）。因此，本文预设一个初始高程平面Z0代入该投影变换，可以计算得到初始平面坐标（X0,Y0）。随后利用该平面坐标内插DEM，可得到更接近真实高程的Z1高程面。迭代上述过程，不断更新高程面，直到反投影误差小于阈值，即可得到精度极高的目标三维坐标。

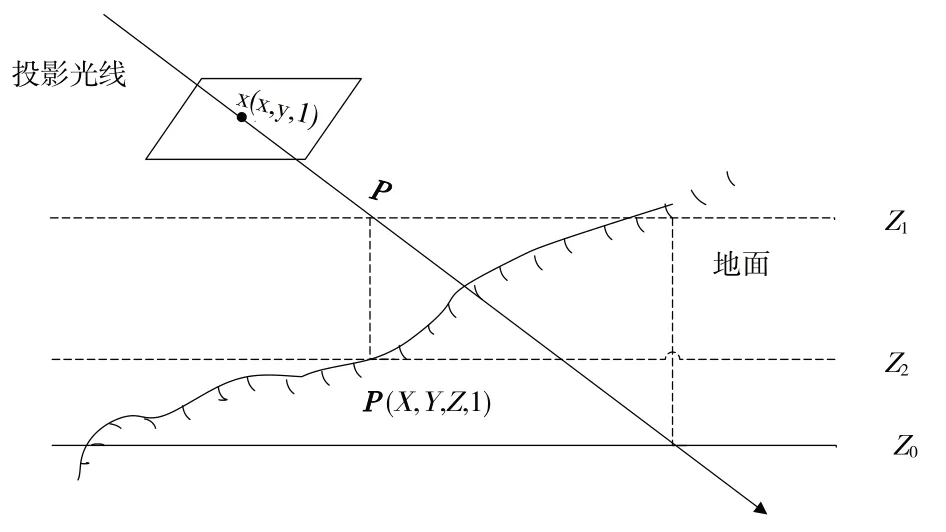
图4 高程迭代逼近过程

2 实验设计

本研究分别选取了摄像头监测范围内不同焦距下，不同范围和场景的3张影像作为待定位的测试影像，以测试本方法在与摄像头不同水平距离，不同焦距及覆盖范围下的定位情况。第一张影像为距离摄像头500 m 左右的区域，覆盖场景直径小于100 m，焦距较大；第二张影像为距离摄像头500 m 左右的区域，地势起伏相对更大，覆盖场景长度达到800～1 000 m，焦距较小；第三张影像为距离摄像头1 000 m左右的区域，覆盖场景长度达到1 000～5 000 m，焦距最小。

实验使用本文研究中的方法对这3 张影像上的点进行定位，输入影像使用基准数据库构建的相同的方法进行刺点，利用检查点验证本文方法。

此外，实验讨论了摄像头内方位元素初始值未知、摄像头内方位元素初始值已知2 种情况，分别使用直接线性变换和共线方程方法进行定向，并对定位结果进行了对比。实验使用的待定位影像及检查点分布图如表1所示。

表1 输入影像及刺点分布

实验采用张正友棋盘格标定法[19]对实验所用摄像头进行内参及畸变系数标定。由于PTZ相机的焦距可变，摄像头在参数T为1.0和2.0的情况下分别进行了标定，得到的内参结果如表2所示。

表2 输入影像及刺点分布

第一张影像的焦距较大，使用焦距为2.0 时的标定结果作为影像内参的初值。第二、三张影像的焦距则使用焦距为1.0时的标定结果作为初值。

3 实验结果及分析

3.1 定位实验

表3 展示了3 张输入的待定位影像以及通过词汇树方法检索到的最相似匹配影像。

表3 输入影像及匹配结果

对于第①组输入影像，其匹配结果如图5 所示；对于第②组输入影像，其匹配结果如图6 所示；对于第③组输入影像，其匹配结果如图7所示。

图5 第一组匹配结果

图6 第二组匹配结果

图7 第三组匹配结果

实验中三组测试影像检查点与DSM交会解算出的坐标对比，得到误差结果如表4、5、6 所示，主要包含三维坐标误差与大地高差。

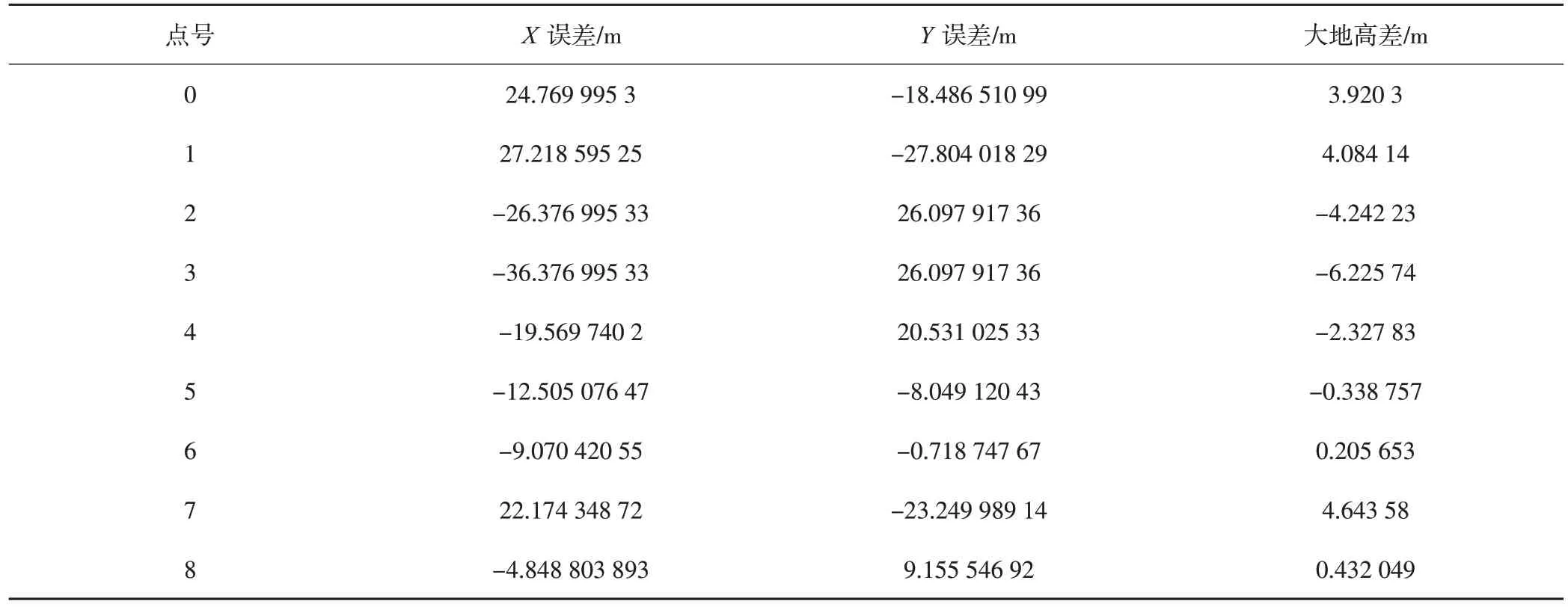
表4 第一组误差表

表5 第二组误差表

表6 第三组误差表

根据上述3 组误差表的分析结果可得出结论：在图像采集范围为500 m 以内时，三维坐标误差平均为20 m 左右，最大不超过40 m，并且大地高差也较小，最大大地高差在6 m 左右；在图像采集范围扩大至1 km 以内时，相对于500 m 范围，坐标误差略有增加，平均在30 m左右，最大不超过60 m。此外，大地高差范围也有所增加，最大误差增加到了8 m 左右；当图像采集范围扩大至5 km 以内时，相对于之前的500 m和1 km范围，坐标误差与实验二基本持平，平均值在30 m左右，最大值不超过60 m，但大地高差的最大误差范围增加到了12 m左右。

随着图像采集范围的增大，大地高差变化相对较小，误差值范围也相对较小。然而，三维坐标误差会呈现一定范围的增加，从而导致定位精度的降低。随着距摄像头水平距离的增加，三维坐标误差和大地高差也随之增加，这可能是因为在距离更远时，摄像头姿态的误差对三维坐标误差的影像会更大。

除此之外，可以注意到有一些点的误差比较大，比如第一组实验中的4 号点，第3 组实验中的1 号点。这可能是因为1 组实验4 号点为房屋顶点，房屋的高度影响了精度，而3 组实验1 号点处在拍摄范围边缘的位置，并且周围房屋较多，因此平面和高程误差较大。

3.2 无内参初值定位实验

不使用相机标定的内参初值，采用直接线性变换方法进行定向，对第二张影像进行定位实验，得到的误差结果如表7。

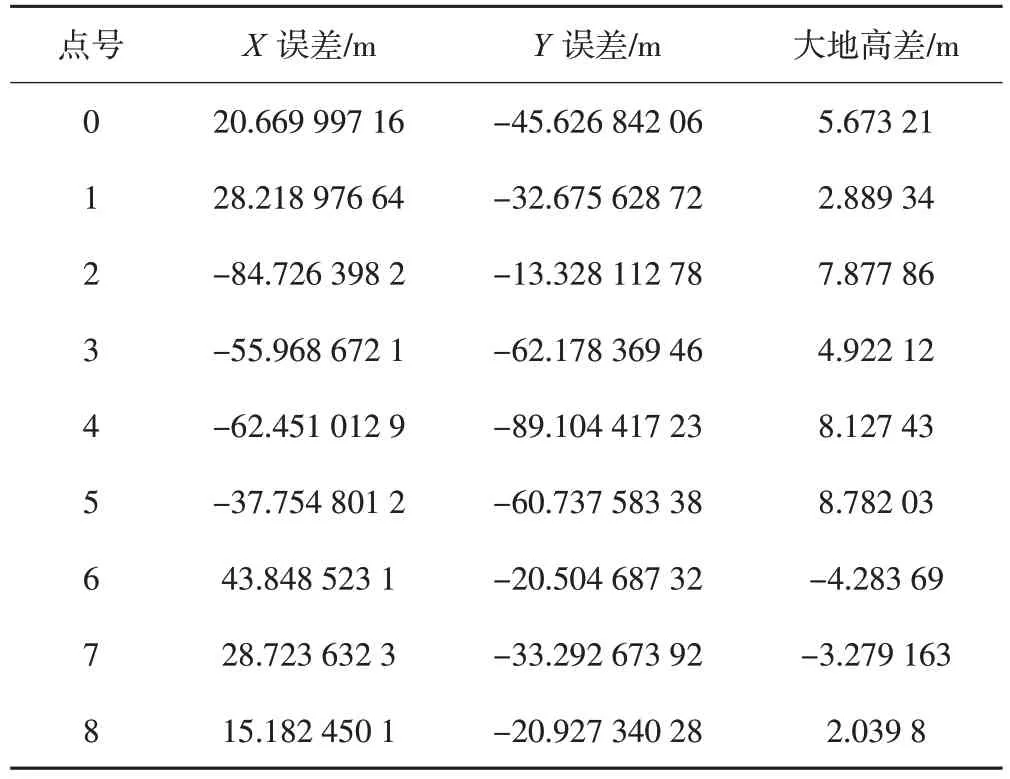
表7 第二组误差表-无内参初值

与采用共线方程所得的结果（表5）相比，在无内参初始值时使用直接线性变换定向得到的定位结果误差明显增加。共线方程使用的模型更加精确，在有内参初值的情况下可以获得更加精确的定位结果。

4 结语和展望

针对单目摄像机的精准定位问题，本研究提出了利用多源空间数据辅助的PTZ 摄像机几何定位方法。该方法通过利用PTZ摄像机对不同焦距和俯仰角进行视频采集，并从采集的视频中抽取视频帧，结合高精度DSM 数据和卫星正射影像进行内业“刺点”，从而减少了布设外业控制点的人力成本。在研究过程中，本文使用分层词汇树检索相似样本控制片影像，并通过特征点提取和双向匹配获取样本控制片的特征点坐标信息；然后，基于后方交会或DLT模型完成影像位姿求解；最后，利用高精度DSM进行迭代求交，以实现定位。该方法借助多源数据辅助定位，旨在确保定位的精度和稳定性。

通过本文的研究结果可知：基于PTZ摄像机的定位方法在图像采集范围增大时，精确度会逐渐降低，误差范围会增大。这表明在较大范围内进行精准定位时，需要进一步改进和优化算法，以提高定位精度并减小误差范围。

随着对定位精度要求的不断提高，本文的研究方法在实现高精度定位方面仍存在一定的限制，尚未能有效满足精密定位的要求。为了进一步提高定位精度，下一步的研究可以集中在改进特征点提取算法和视频帧的抽取方法上，以实现更精准的定位结果。